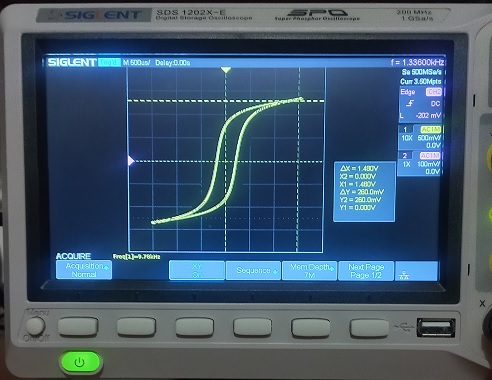
Questo
sistema permette di visualizzare il ciclo di isteresi magnetica sullo
schermo dell'oscilloscopio, lo schema del sistema è il seguente:
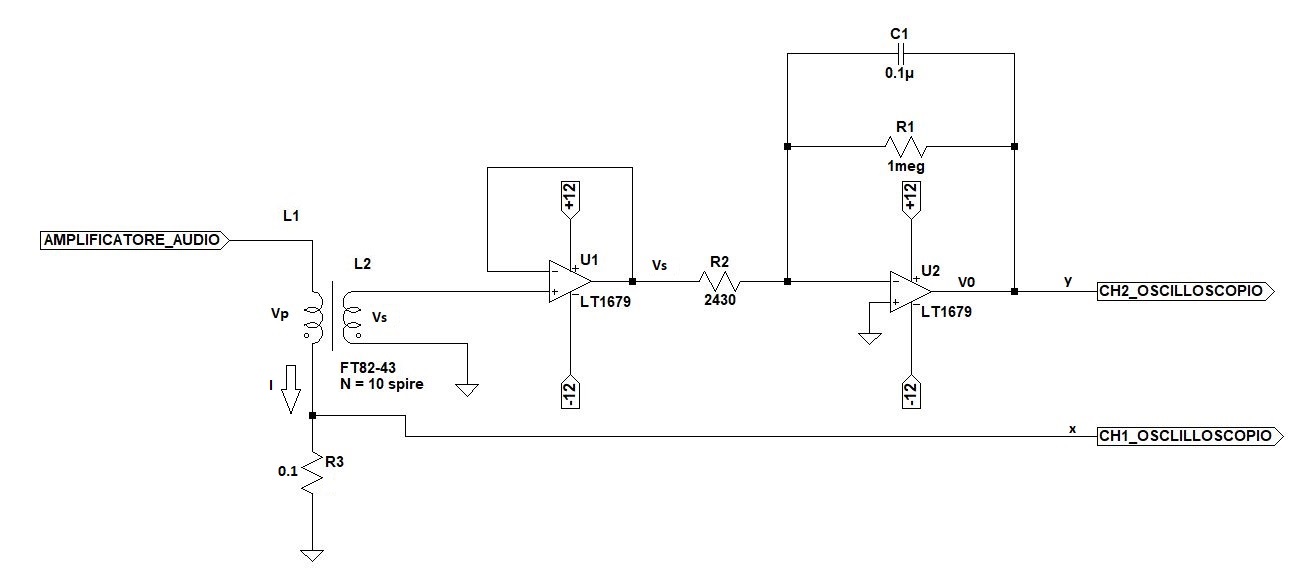
Per eseguire l'esperienza occorrono i seguenti strumenti:
1) Un generatore di funzioni .
2) Un amplificatore audio di potenza.
3) Una resistenza di 0.1 ohm 1% 1W (per misurare correnti dell'ordine dei 3 A).
4) Due operazionali a basso rumore (in genere contenuti in un solo chip).
5) Un oscilloscopio (possibilmente digitale).
NOTA:
L'oscilloscopio va impostato sul modo X-Y. La sonda inserita nel canale CH1 deve essere impostata a X1 e l'ingresso dello stesso canale a X10. L'accoppiamento del canale CH2 deve essere in AC.
Per eseguire l'esperienza occorrono i seguenti strumenti:
1) Un generatore di funzioni .
2) Un amplificatore audio di potenza.
3) Una resistenza di 0.1 ohm 1% 1W (per misurare correnti dell'ordine dei 3 A).
4) Due operazionali a basso rumore (in genere contenuti in un solo chip).
5) Un oscilloscopio (possibilmente digitale).
NOTA:
L'oscilloscopio va impostato sul modo X-Y. La sonda inserita nel canale CH1 deve essere impostata a X1 e l'ingresso dello stesso canale a X10. L'accoppiamento del canale CH2 deve essere in AC.
COME FUNZIONA
Il
segnale audio, fornito dall'amplificatore di potenza, alimenta la serie composta dal primario e
dalla resistenza R3, la corrente I
circolando nella resistenza provoca in essa una caduta pari a 0.1 * I volt.
Con l'ingresso CH1 impostato a X10, l'oscilloscopio legge direttamente il valore di questa corrente che viene visualizzata sull'asse X , per ottenere il campo magnetico H bisogna applicare la seguente nota formula:
H = N * I / le (amperspire / metro) [1]
dove:
N = numero di spire
I = corrente letta sul canale CH1 (ampere)
le = percorso mediano del flusso nel nucleo ferromagnetico (metri)
Quindi con una diretta lettura sullo schermo dell'oscilloscopio e una semplice operazione matematica ottengo il campo magnetico H.
Il flusso magnetico è in relazione con la tensione primaria Vp(t) come segue:
Ø(t) = Integrale (Vp(t) / N) * dt (weber) [2]
ovvero il flusso è l'integrale della tensione divisa per il numero di spire.
Se la tensione al primario è sinusoidale (questo è vero fintanto la resistenza di uscita dell'amplificatore, la resistenza R3 e quella del filo sono trascurabili rispetto alla reattanza induttiva) ha il seguente andamento:
Vp(t) = VpM * sin(w * t) (volt) [3]
dove
VpM = valor massimo della tensione primaria.
w = pulsazione (2 * Pi * f) (rad/sec)
t = tempo istantaneo (sec)
f = frequenza (Hz)
Integrando questa funzione ottengo il flusso:
Ø(t) = [VpM / (N * w)] * cos(w * t) (weber) [4]
dove:
N = numero di spire
VpM / (N * w) = ØM valor massimo del flusso (weber)
Dato che lavoreremo con i valori massimi è bene notare che il valor massimo del flusso è inversamente proporzionale alla pulsazione w e quindi alla frequenza, questo significa che a parità di tensione VpM aumentando la frequenza il flusso diminuisce e diminuendo la frequenza il flusso aumenta. Dato che il flusso è legato all'induzione magnetica B questo semplice fenomeno ci fa intendere che a parità di induzione magnetica il valore di tensione da applicare al primario deve aumentare con la frequenza e viceversa. Questo è ovvio dato che all'aumentare della frequenza la reattanza induttiva aumenta e a parità di corrente (che è legata all'induzione attraverso il campo magnetico H) la tensione deve aumentare per mantenere costante l'induzione stessa.
Dividendo ambo i membri della [4] per Ae (area trasversale del nucleo) ottengo la relazione tra l'induzione BM (valore massimo) e la tensione VpM:
BM = VpM / (N * w * Ae) (tesla) [5]
Bisogna ricordare che la [5] è valida solo per segnali sinusoidali (o quasi sinusoidali), inoltre in essa non compare l'induttanza dell'avvolgimento (che varia con il livello del campo H) per cui la formula è lineare e non tiene conto della saturazione del nucleo.
Per questo motivo se applicate la [5] a frequenze molto basse (dove la reattanza induttiva è paragonabile alle resistenze elettriche complessive (quella di uscita dell'amplificatore, la resistenza R3 e quella del filo) otterrete risultati errati, quando useremo questa formula per tarare il trimmer R2 bisognerà fare attenzione che la Vp(t) sia sinusoidale, per questo sarà sufficiente fare le prove alle frequenze più alte e controllare la forma del segnale con l'oscilloscopio prima di iniziare la taratura.
L'integrazione [2] viene effettuata dall'integrato U2, la sua funzione di trasferimento è la seguente:
V0 = VpM / (w * C1 * R2) (volt) [6]
Se il coefficiente di accoppiamento è vicino alla unità si può ritenere:
VsM = VpM [7]
Consiglio di fare le prove su toroidi dato che in essi il coefficiente di accoppiamento è molto vicino all'unità.
Quindi la [6] si può riscrivere così:
V0 = VsM / (w * C1 * R1) (volt) [8]
dalla [5] sostituendo VpM con VsM ottengo la tensione secondaria:
VsM = (N * w * Ae) * BM (volt) [9]
Sostituendo la [9] nella [6]:
V0 = (N * w * Ae) * BM / (w * C1 * R1) (volt) [10]
La pulsazione w si elide e ottengo:
BM = V0 * C1 * R1 / (N * Ae) (tesla) [11]
ponendo
C1 * R2 = N * Ae [12]
si ottiene:
BM = V0 (tesla) [13]
Ovvero, l'oscilloscopio legge sul CH2 direttamente il valore dell' induzione B e la visualizza sull'asse Y.
Quindi ricapitolando:
Sul canale CH1 l'oscilloscopio legge direttamente la corrente e la visualizza sull'asse X e sul CH2 legge direttamente l'induzione B e la visualizza sull'asse Y, abbiamo la nostra isteresi.
Dalla [12] possiamo ricavare la resistenza R2 da un valore prefissato di C1 o viceversa ma bisogna fare alcune premesse prima. Ho interposto un buffer tra l'avvolgimento secondario e l'ingresso dell'integratore per poter far sì che nell'avvolgimento secondario non circoli corrente (per una corretta visualizzazione della isteresi occorre che la corrente sia solo quella primaria e non quella primaria sommata a quella trasferita dal secondario al primario). Il datat sheet del LT1679 dice che la massima corrente che può erogare l'integrato è di 20 mA (min) e che la massima tensione in modo comune è circa 11V (con alimentazione a +/- 12V), quindi la minima resistenza R2 che può alimentare integrato U1 è:
Rv = 11 / 0.02 = 550 (ohm) [14]
L'integratore è in poche parole un filtro passa basso con pendenza 6dB / ottava, la frequenza di taglio (sotto la quale l'integrato non funziona più come integratore) è:
ft = 1 / ( 2 * Pi * C1 * R1) (Hz) [15]
dove:
ft = frequenza di taglio (Hz)
R1 = resistenza per dare un guadagno finito alle basse frequenze (ohm)
scegliendo, ad esempio, una capacità di 0.1 uF ottengo il taglio a:
ft = 1 / ( 2 * Pi * 0.1 * 10 ^(-6) * 10^6) (Hz) = 10 Hz [16]
Quindi il ciclo di isteresi potrà essere visualizzato correttamente da qualcosa di più di 10 Hz in su. Prima di calcolare la resistenza R2 occorre determinare in giusto numero di spire N. Per farlo uso la [5]:
N = VpM / (BM * w * Ae) (spire) [17]
Per avere idea a che valore di induzione il materiale entra in saturazione dobbiamo leggere il suo datascheet. Per fare le prove ho scelto il materiale 43 di ferrite, la foto sotto visualizza il ciclo di isteresi:
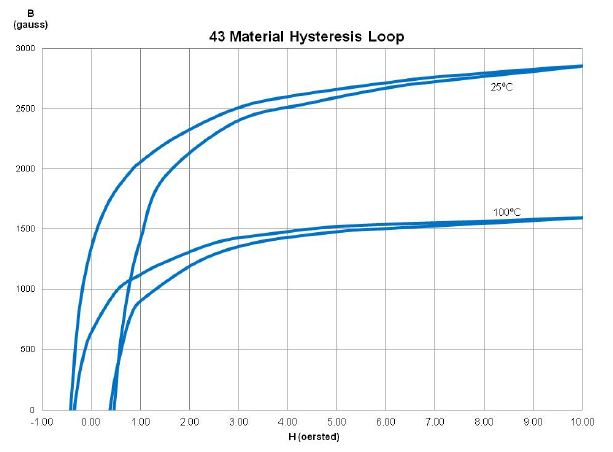
Scegliendo il valore di campo H massimo (10 Oe a 25 °C) si legge che il B corrispondente è circa 2900 Gaus (0.29 tesla). Tenendo conto che la tensione massima che può essere accettata dall'integrato è 11V si può scegliere una frequenza massima a piacimento per determinare N. Io ho scelto 25000Hz. Allora:
N = VpM / (BM * w * Ae) = 11 / (0.29 * 2 * Pi * 25000 * 0.0000243) = 10 (spire) [18]
Dove:
VpM = VsM = valore massimo di tensione accettata dall'integrato (volt)
Ae = Area trasversale del toroide. (metri)
BM = induzione per nucleo in profonda saturazione (tesla)
Ora tramite la [12] determino la resistenza R2:
R2 = N * Ae / C1 = 10 * 0.0000243 / 0.1 * 10 ^(-6) = 2430 ohm [19]
Questo valore è superiore a quello della resistenza minima che si può usare [14] e va quindi bene. Ovviamente al posto di R2 conviene mettere un trimmer per la tolleranza dei componenti e occorre tararlo.
Per la taratura del trimmer la tensione Vp(t) deve essere sinusoidale (controllatela con l'oscilloscopio), a parità di BM più è alta la frequenza e più la forma della tensione si avvicina a quella sinusoidale. Abbassate il livello della tensione d'ingresso per allontanare il nucleo dalla saturazione, per il materiale 43 è sufficiente che B sia intorno ai 0.2 tesla.
Visualizzate sull'oscilloscopio la tensione Vs(t) (spostando momentaneamente la sonda da V0(t) a Vs(t)), leggete il valor massimo della tensione. Applicate la [5] per determinare l'induzione massima corrispondente a quel valore di tensione. Ad esempio io ho letto 1.66V a 5000 Hz, inserendo questi due valori nella seguente formula ho ottenuto BM:
BM = VpM / (N * w * Ae) = 1.66/ (10 * 2 * Pi * 5000 * 0.0000243) = 0.217 tesla [20]
Rimettete la sonda dell'oscilloscopio su V0(t) e tarate R2 per portare B al valore ricavato dalla formula come nella seguente foto. Da questo momento in poi il sistema è tarato e potrete fare tutte le prove che vorrete sul materiale da voi scelto con segnali di qualsiasi forma (quella sinusoidale serve solo per la taratura).

Alcune osservazioni:
per quanto riguarda il filo di rame potete scegliere la sezione che volete, io personalmente uso sempre la stessa regola anche quando non serve come in questo caso, ovvero scelgo una sezione del filo il cui raggio è pari alla profondità di penetrazione dovuta all'effetto pelle così da avere sempre la sicurezza che la resistenza in continua e quella in alternata sono uguali.
Nella tabella seguente viene indicato in numero awg del filo il cui raggio corrisponde alla profondità di penetrazione per una certa frequenza.
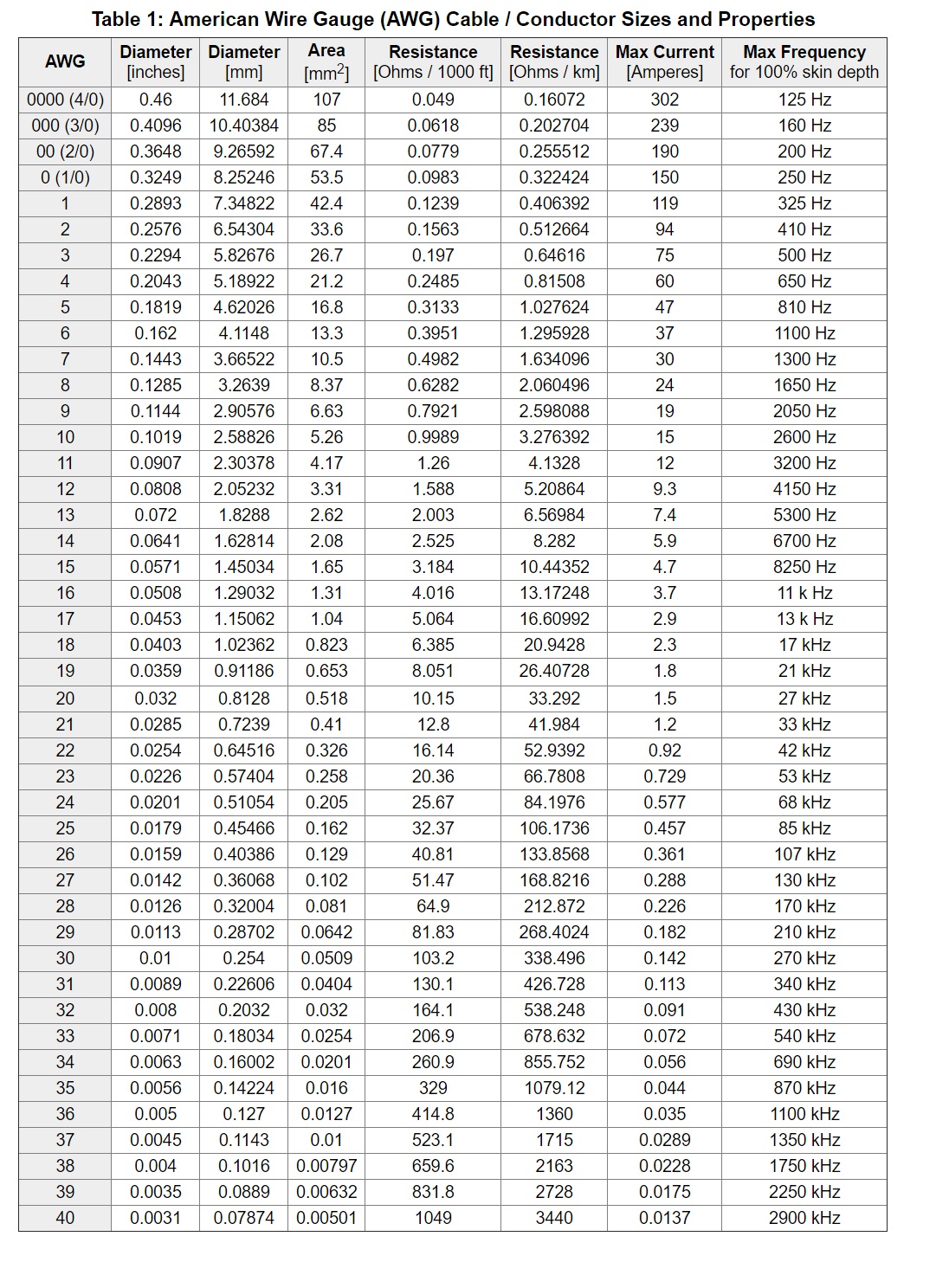
La frequenza che ho scelto [18] è 25 KHz e si trova tra 21 KHz e 27 KHz, scelgo AWG 19 con una leggero spreco di rame.
Per quanto riguarda l'amplificatore audio occorre essere sicuri che riesca a sostenere il picco di corrente quando il materiale è in profonda saturazione. Ad esempio nella figura sottostante è rappresentata l'isteresi in profonda saturazione a 25 KHz.
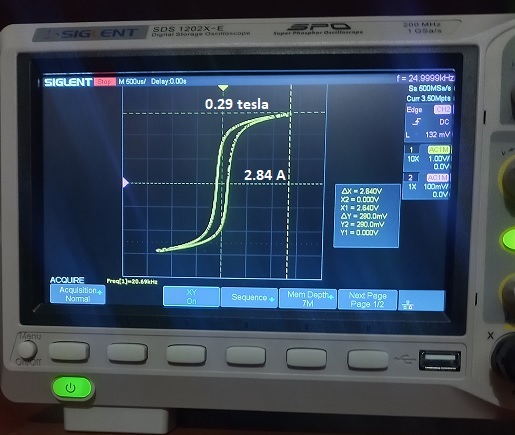
Per avere una induzione di 0.29 tesla occorrono 2.84 A di picco, il mio amplificatore riesce ad erogare fino a 3.5 A senza distorcere e quindi va bene.
Nella foto seguente si nota una leggera distorsione sul segnale tensione a 25 Khz quando il nucleo è in profonda saturazione (alle basse frequenze la distorsione aumenta notevolmente a parità di BM). Per questo se provate a usare la [20] per determinare l'induzione BM troverete delle incongruenze tra il valore determinato e quello visualizzato sullo schermo come già detto prima.
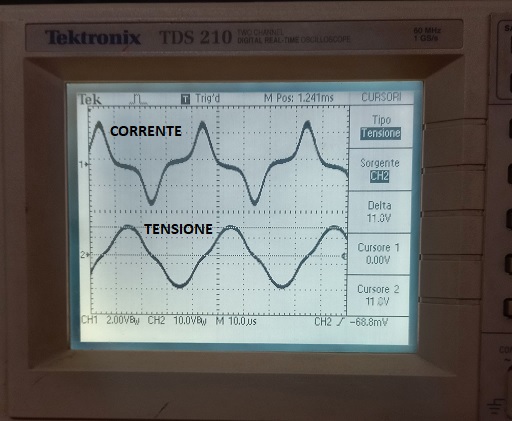
Nella seguente foto è visualizzata la isteresi quando si supera il massimo livello di tensione consentito dall'integrato per cercare di portare l'induzione BM a 0.29 tesla ma a frequenza più alta di 25 KHz.
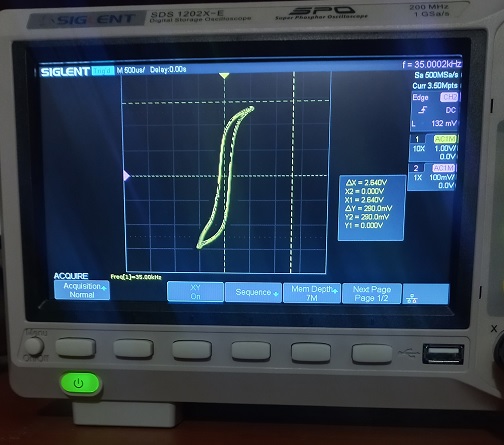
Si nota un rigonfiamento nella parte negativa e la compressione in quella positiva. L'integrato non riesce più a lavorare bene a causa dell'eccessivo livello in ingresso e si comporta in maniera imprevedibile.
Neella foto seguente il toroide in ferrite FT82-43 sotto esame.

Spero che questa esperienza vi abbia interessato.
Fabio
Con l'ingresso CH1 impostato a X10, l'oscilloscopio legge direttamente il valore di questa corrente che viene visualizzata sull'asse X , per ottenere il campo magnetico H bisogna applicare la seguente nota formula:
H = N * I / le (amperspire / metro) [1]
dove:
N = numero di spire
I = corrente letta sul canale CH1 (ampere)
le = percorso mediano del flusso nel nucleo ferromagnetico (metri)
Quindi con una diretta lettura sullo schermo dell'oscilloscopio e una semplice operazione matematica ottengo il campo magnetico H.
Il flusso magnetico è in relazione con la tensione primaria Vp(t) come segue:
Ø(t) = Integrale (Vp(t) / N) * dt (weber) [2]
ovvero il flusso è l'integrale della tensione divisa per il numero di spire.
Se la tensione al primario è sinusoidale (questo è vero fintanto la resistenza di uscita dell'amplificatore, la resistenza R3 e quella del filo sono trascurabili rispetto alla reattanza induttiva) ha il seguente andamento:
Vp(t) = VpM * sin(w * t) (volt) [3]
dove
VpM = valor massimo della tensione primaria.
w = pulsazione (2 * Pi * f) (rad/sec)
t = tempo istantaneo (sec)
f = frequenza (Hz)
Integrando questa funzione ottengo il flusso:
Ø(t) = [VpM / (N * w)] * cos(w * t) (weber) [4]
dove:
N = numero di spire
VpM / (N * w) = ØM valor massimo del flusso (weber)
Dato che lavoreremo con i valori massimi è bene notare che il valor massimo del flusso è inversamente proporzionale alla pulsazione w e quindi alla frequenza, questo significa che a parità di tensione VpM aumentando la frequenza il flusso diminuisce e diminuendo la frequenza il flusso aumenta. Dato che il flusso è legato all'induzione magnetica B questo semplice fenomeno ci fa intendere che a parità di induzione magnetica il valore di tensione da applicare al primario deve aumentare con la frequenza e viceversa. Questo è ovvio dato che all'aumentare della frequenza la reattanza induttiva aumenta e a parità di corrente (che è legata all'induzione attraverso il campo magnetico H) la tensione deve aumentare per mantenere costante l'induzione stessa.
Dividendo ambo i membri della [4] per Ae (area trasversale del nucleo) ottengo la relazione tra l'induzione BM (valore massimo) e la tensione VpM:
BM = VpM / (N * w * Ae) (tesla) [5]
Bisogna ricordare che la [5] è valida solo per segnali sinusoidali (o quasi sinusoidali), inoltre in essa non compare l'induttanza dell'avvolgimento (che varia con il livello del campo H) per cui la formula è lineare e non tiene conto della saturazione del nucleo.
Per questo motivo se applicate la [5] a frequenze molto basse (dove la reattanza induttiva è paragonabile alle resistenze elettriche complessive (quella di uscita dell'amplificatore, la resistenza R3 e quella del filo) otterrete risultati errati, quando useremo questa formula per tarare il trimmer R2 bisognerà fare attenzione che la Vp(t) sia sinusoidale, per questo sarà sufficiente fare le prove alle frequenze più alte e controllare la forma del segnale con l'oscilloscopio prima di iniziare la taratura.
L'integrazione [2] viene effettuata dall'integrato U2, la sua funzione di trasferimento è la seguente:
V0 = VpM / (w * C1 * R2) (volt) [6]
Se il coefficiente di accoppiamento è vicino alla unità si può ritenere:
VsM = VpM [7]
Consiglio di fare le prove su toroidi dato che in essi il coefficiente di accoppiamento è molto vicino all'unità.
Quindi la [6] si può riscrivere così:
V0 = VsM / (w * C1 * R1) (volt) [8]
dalla [5] sostituendo VpM con VsM ottengo la tensione secondaria:
VsM = (N * w * Ae) * BM (volt) [9]
Sostituendo la [9] nella [6]:
V0 = (N * w * Ae) * BM / (w * C1 * R1) (volt) [10]
La pulsazione w si elide e ottengo:
BM = V0 * C1 * R1 / (N * Ae) (tesla) [11]
ponendo
C1 * R2 = N * Ae [12]
si ottiene:
BM = V0 (tesla) [13]
Ovvero, l'oscilloscopio legge sul CH2 direttamente il valore dell' induzione B e la visualizza sull'asse Y.
Quindi ricapitolando:
Sul canale CH1 l'oscilloscopio legge direttamente la corrente e la visualizza sull'asse X e sul CH2 legge direttamente l'induzione B e la visualizza sull'asse Y, abbiamo la nostra isteresi.
Dalla [12] possiamo ricavare la resistenza R2 da un valore prefissato di C1 o viceversa ma bisogna fare alcune premesse prima. Ho interposto un buffer tra l'avvolgimento secondario e l'ingresso dell'integratore per poter far sì che nell'avvolgimento secondario non circoli corrente (per una corretta visualizzazione della isteresi occorre che la corrente sia solo quella primaria e non quella primaria sommata a quella trasferita dal secondario al primario). Il datat sheet del LT1679 dice che la massima corrente che può erogare l'integrato è di 20 mA (min) e che la massima tensione in modo comune è circa 11V (con alimentazione a +/- 12V), quindi la minima resistenza R2 che può alimentare integrato U1 è:
Rv = 11 / 0.02 = 550 (ohm) [14]
L'integratore è in poche parole un filtro passa basso con pendenza 6dB / ottava, la frequenza di taglio (sotto la quale l'integrato non funziona più come integratore) è:
ft = 1 / ( 2 * Pi * C1 * R1) (Hz) [15]
dove:
ft = frequenza di taglio (Hz)
R1 = resistenza per dare un guadagno finito alle basse frequenze (ohm)
scegliendo, ad esempio, una capacità di 0.1 uF ottengo il taglio a:
ft = 1 / ( 2 * Pi * 0.1 * 10 ^(-6) * 10^6) (Hz) = 10 Hz [16]
Quindi il ciclo di isteresi potrà essere visualizzato correttamente da qualcosa di più di 10 Hz in su. Prima di calcolare la resistenza R2 occorre determinare in giusto numero di spire N. Per farlo uso la [5]:
N = VpM / (BM * w * Ae) (spire) [17]
Per avere idea a che valore di induzione il materiale entra in saturazione dobbiamo leggere il suo datascheet. Per fare le prove ho scelto il materiale 43 di ferrite, la foto sotto visualizza il ciclo di isteresi:
Scegliendo il valore di campo H massimo (10 Oe a 25 °C) si legge che il B corrispondente è circa 2900 Gaus (0.29 tesla). Tenendo conto che la tensione massima che può essere accettata dall'integrato è 11V si può scegliere una frequenza massima a piacimento per determinare N. Io ho scelto 25000Hz. Allora:
N = VpM / (BM * w * Ae) = 11 / (0.29 * 2 * Pi * 25000 * 0.0000243) = 10 (spire) [18]
Dove:
VpM = VsM = valore massimo di tensione accettata dall'integrato (volt)
Ae = Area trasversale del toroide. (metri)
BM = induzione per nucleo in profonda saturazione (tesla)
Ora tramite la [12] determino la resistenza R2:
R2 = N * Ae / C1 = 10 * 0.0000243 / 0.1 * 10 ^(-6) = 2430 ohm [19]
Questo valore è superiore a quello della resistenza minima che si può usare [14] e va quindi bene. Ovviamente al posto di R2 conviene mettere un trimmer per la tolleranza dei componenti e occorre tararlo.
Per la taratura del trimmer la tensione Vp(t) deve essere sinusoidale (controllatela con l'oscilloscopio), a parità di BM più è alta la frequenza e più la forma della tensione si avvicina a quella sinusoidale. Abbassate il livello della tensione d'ingresso per allontanare il nucleo dalla saturazione, per il materiale 43 è sufficiente che B sia intorno ai 0.2 tesla.
Visualizzate sull'oscilloscopio la tensione Vs(t) (spostando momentaneamente la sonda da V0(t) a Vs(t)), leggete il valor massimo della tensione. Applicate la [5] per determinare l'induzione massima corrispondente a quel valore di tensione. Ad esempio io ho letto 1.66V a 5000 Hz, inserendo questi due valori nella seguente formula ho ottenuto BM:
BM = VpM / (N * w * Ae) = 1.66/ (10 * 2 * Pi * 5000 * 0.0000243) = 0.217 tesla [20]
Rimettete la sonda dell'oscilloscopio su V0(t) e tarate R2 per portare B al valore ricavato dalla formula come nella seguente foto. Da questo momento in poi il sistema è tarato e potrete fare tutte le prove che vorrete sul materiale da voi scelto con segnali di qualsiasi forma (quella sinusoidale serve solo per la taratura).

Alcune osservazioni:
per quanto riguarda il filo di rame potete scegliere la sezione che volete, io personalmente uso sempre la stessa regola anche quando non serve come in questo caso, ovvero scelgo una sezione del filo il cui raggio è pari alla profondità di penetrazione dovuta all'effetto pelle così da avere sempre la sicurezza che la resistenza in continua e quella in alternata sono uguali.
Nella tabella seguente viene indicato in numero awg del filo il cui raggio corrisponde alla profondità di penetrazione per una certa frequenza.

La frequenza che ho scelto [18] è 25 KHz e si trova tra 21 KHz e 27 KHz, scelgo AWG 19 con una leggero spreco di rame.
Per quanto riguarda l'amplificatore audio occorre essere sicuri che riesca a sostenere il picco di corrente quando il materiale è in profonda saturazione. Ad esempio nella figura sottostante è rappresentata l'isteresi in profonda saturazione a 25 KHz.

Per avere una induzione di 0.29 tesla occorrono 2.84 A di picco, il mio amplificatore riesce ad erogare fino a 3.5 A senza distorcere e quindi va bene.
Nella foto seguente si nota una leggera distorsione sul segnale tensione a 25 Khz quando il nucleo è in profonda saturazione (alle basse frequenze la distorsione aumenta notevolmente a parità di BM). Per questo se provate a usare la [20] per determinare l'induzione BM troverete delle incongruenze tra il valore determinato e quello visualizzato sullo schermo come già detto prima.

Nella seguente foto è visualizzata la isteresi quando si supera il massimo livello di tensione consentito dall'integrato per cercare di portare l'induzione BM a 0.29 tesla ma a frequenza più alta di 25 KHz.

Si nota un rigonfiamento nella parte negativa e la compressione in quella positiva. L'integrato non riesce più a lavorare bene a causa dell'eccessivo livello in ingresso e si comporta in maniera imprevedibile.
Neella foto seguente il toroide in ferrite FT82-43 sotto esame.

Spero che questa esperienza vi abbia interessato.
Fabio