
Mi
piace moltissimo lavorare con i circuiti ad alta frequenza perché
con loro niente è scontato, delle volte sembra che lo studio
analitico, in fase progettuale, sia un qualcosa di inutile ed estraneo
al prodotto finale; valori generati dalle formule che non si accordano
con quelli misurati, previsioni matematiche completamente sovvertite da comportamenti imprevedibili
del circuito. Alla fine il tempo passato in laboratorio è enorme rispetto a quello
passato davanti al computer o ad un pezzo di carta per simulare o
formulare.
Ma da quale frequenza iniziano i capricci tra teoria e pratica? Beh, da quando cominciano a farsi sentire gli elementi parassiti di tipo reattivo nei componenti e nei collegamenti, per dare un valore numerico diciamo da 1 MHz in su. Altre volte forme che ci aspettavamo essere sinusoidali hanno in realtà un aspetto orribile, brutte, con andamento inaspettato e condito da strani picchi, non si capisce se ciò sia dovuto ad un mal funzionamento del circuito o dalla sonda rotta, poi spostiamo il coccodrilletto di massa di quest'ultima su un alto punto ed ecco che appare sull'oscilloscopio una bella sinusoide come avrebbe dovuto essere. Questa, e non solo, è l'alta frequenza.
Inoltre consiglio vivamente di non spostare più i componenti sensibili una volta che il circuito funziona bene, può capitare che ci si accorga che il reoforo di un condensatore (del gruppo risonante ad esempio) sia troppo tirato e per paura che si possa rompere lo si saldi in un altro punto dove sia meno stressato. Dopo la modifica è probabile che il circuito non funzioni più.
D'altronde da qualche parte bisogna pur iniziare e la componente analitica di tutto il processo è comunque la parte più indicata per farlo, la premessa sopra serve solo a mettere in guardia i neofiti avventurieri dell'alta frequenza delle possibili delusioni che potrebbero provare una volta data alimentazione al circuito.
L'oscillatore che tratto in questa pagina è del tipo a base comune, lo schema è riportato nella figura seguente.
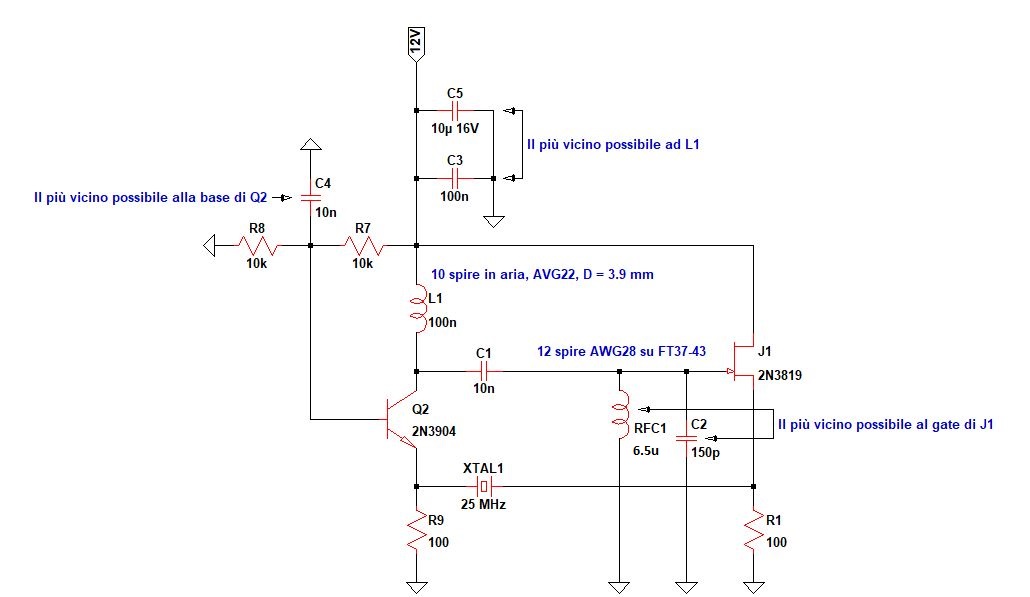
Le resistenze R7, R8 e R9 servono per polarizzare il transistor Q2 in zona attiva, la resistenza R1 e l'induttanza RFC1 servono per polarizzare il JFET in zona attiva, la RFC deve presentare una alta reattanza alla frequenza di 25 MHz. Il condensatore C4 serve per mettere a massa la base in modo che la connessione del BJT sia, appunto, a base comune, esso deve presentare una bassa reattanza a 25 MHz. Il condensatore C1 serve per evitare che la continua presente sul collettore di Q1 alimenti il gate di J1, esso deve presentare una bassa reattanza a 25 MHz. I condensatori C5 e C3 servono a bypassare l'alimentazione essi devono presentare una bassa reattanza a 25 MHz, questi due condensatori, apparentemente banali, hanno invece una notevole importanza soprattutto quando l'alimentatore non presenta una bassa impedenza a 25 MHz.
L'oscillazione si genera solo a quella frequenza alla quale la tensione presente al collettore del BJT risulta in fase con quella presente al suo emettitore, in tal modo si instaura una retroazione positiva tra ingresso e uscita. Nel nostro caso questo accade solo quando il gruppo L1 C2 ed il quarzo risuonano a 25 MHz. La frequenza di oscillazione è decisa però solo dal quarzo che ha un Q molto più elevato del circuito risonante, quest'ultimo serve solo a presentare al collettore del transistor una impedenza molto alta a fase zero, infatti, se mentre il circuito è in funzione provate a disaccordare il gruppo L1 C2 (di poco se no l'oscillazione scompare) non cambierà la frequenza di oscillazione ma solo il livello del segnale.
Se invece si toglie il quarzo e si collega direttamente il source di J1 all'emettitore di Q2 (tramite condensatore) il circuito oscillerà alla frequenza di risonanza decisa dal gruppo L1 C2.
Il gruppo risonante L1 C2 è del tipo parallelo, per un ottimo Q dovrebbe avere una induttanza piccola e una capacità grande e vedere ai suoi capi una elevata resistenza, l'induttanza non si può però scegliere troppo piccola per evidenti difficoltà costruttive e per evitare che predominino le induttanze distribuite (più difficili da gestire) rispetto a quella concentrata in un punto. Ho scelto un valore di 100nH, un buon compromesso. Nonostante questa scelta le induttanze parassite si fanno sentire tanto che conviene posizionare il condensatore C2 vicinissimo al gate di J1 in modo che possa entrare in risonanza con la complessiva induttanza che vede. Se invece C2 si mettesse vicino a L1 accadrebbe che esso andrebbe in risonanza con la induttanza concentrata e le restanti distribuite rimarrebbero fuori al circuito risonante e si porrebbero lungo il percorso in casuali (dipendendo da come è stato realizzato il circuito) connessioni serie parallelo con conseguenze disastrose per il livello del segnale.
Diversamente dal circuito risonante parallelo quello del quarzo è del tipo serie, per avere un alto Q il quarzo deve vedere una resistenza molto bassa il che è assicurato sia dall'source di J1 che dall'emettitore di Q2, infatti entrambi offrono una resistenza dell'ordine di poche decine di ohm.
Ma entriamo ora nei particolari. Nella figura sottostante è raffigurato il circuito equivalente del circuito per i soli segnali dinamici. Il riquadro attorno a Q2 e a J1 riguarda rispettivamente il transistor ed il JFET vero e proprio con le loro impedenze di ingresso e di uscita, queste le ho ricavate tramite il simulatore LTSpice a 25 MHz quindi il loro valore è approssimato ma sufficientemente vicino alla realtà per quello che serve a noi.
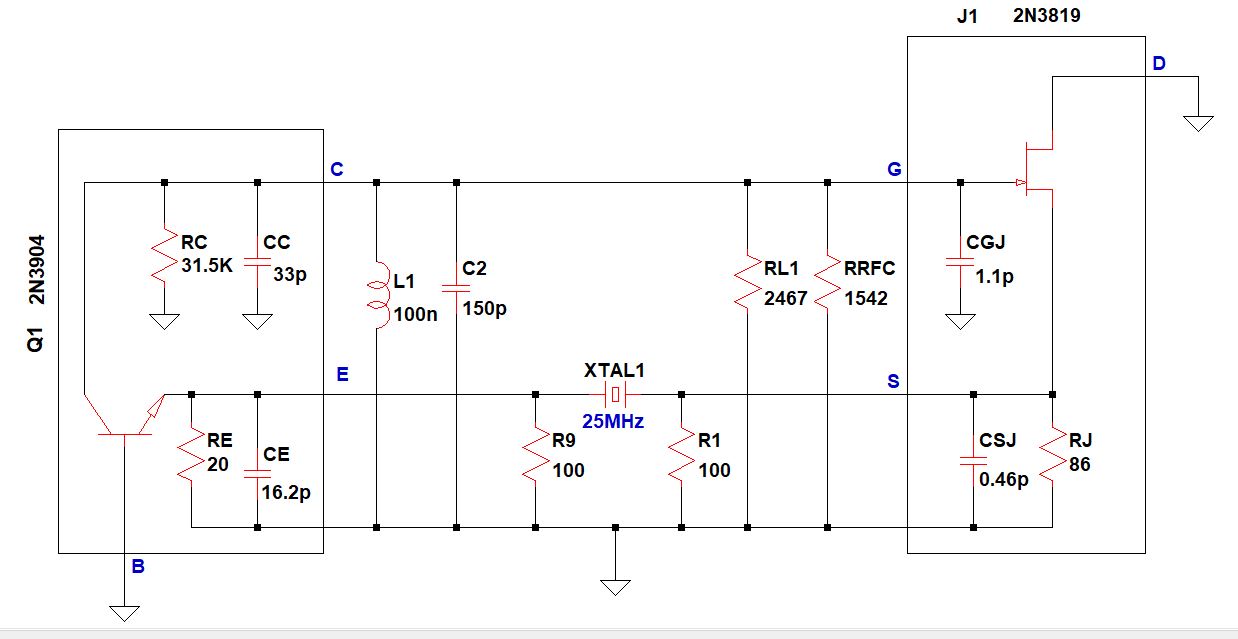
Dove:
RC e CC sono rispettivamente la resistenza e la capacità di uscita del transistor.
RE e CE sono rispettivamente la resistenza e la capacità d'ingresso del transistor.
CGj è la capacità d'ingresso del JFET.
RJ e CSJ sono rispettivamente la resistenza e la capacità di uscita del JFET.
RL1 è la resistenza equivalente parallelo di L1.
RRFC è la resistenza equivalente parallelo della RFC.
Non ho riportato la resistenza di ingresso del JFT perché essendo molto alta può essere trascurata. Non ho riportato neppure l'induttanza RFC1 dato che quest'ultima ha valore (47u) molto più alto rispetto a quello di L1 (100n), a proposito della RFC due parole vanno spese, per determinare il giusto valore ho avvolto qualche spira sul toroide e ho misurato la tensione sul gate del JFET, poi qualche altra spira e ho misurato di nuovo la tensione, se questa era di valore maggiore a quella misurata precedentemente ho seguitato ad avvolgere spire e così via fino a quando il livello di tensione si è stabilizzato. A quel punto ho contato il numero delle spire avvolte e ne ho ricavato il valore induttivo, 6.5 uH (circa 12 spire).
Ovviamente potevo usare, al posto della RFC, una resistenza di pari valore ma ho pensato che sarebbe stato ideale disporre di un toroide per poter adattare un carico di valore a piacimento alla resistenza di uscita complessiva per il massimo trasferimento di potenza.
L'ultima cosa da dire sulle induttanze è che purtroppo a causa dell'effetto pelle e di prossimità la resistenza serie dei conduttori che le compongono non è trascurabile e bisogna tenerne conto trasformandola in resistenza equivalente parallelo, le due resistenze nello schema dinamico sono RL1 per L1 e RRFC per la RFC.
Il gruppo risonante L1C2 allora vede il parallelo di RC, RL1 e RRFC pari a 921 ohm che gli permette di possedere un Q di circa 58:
Per quanto riguarda le capacità CC e CGJ esse vengono inglobate in C2 e vengono a far quindi parte del circuito risonante. A tal proposito queste, quelle parassite assieme alla non precisa realizzazione dell'induttanza L1 più le induttanze parassite che rientrano nel circuito risonante fanno scostare di molto il valore teorico calcolato di C2 che avrebbe dovuto essere circa 405 pF:
I quarzo vede una resistenza complessiva di 62.9 ohm che gli permette di possedere un Q di circa 10000, le capacità CSJ e CE vengono viste dal quarzo in serie e assumono un valore complessivo di circa 0.4 pF che assieme a quelle parassite (di pochi pico) non disturbano affatto il quarzo stesso.
Nella figura sottostante è raffigurato il circuito dinamico in risonanza.
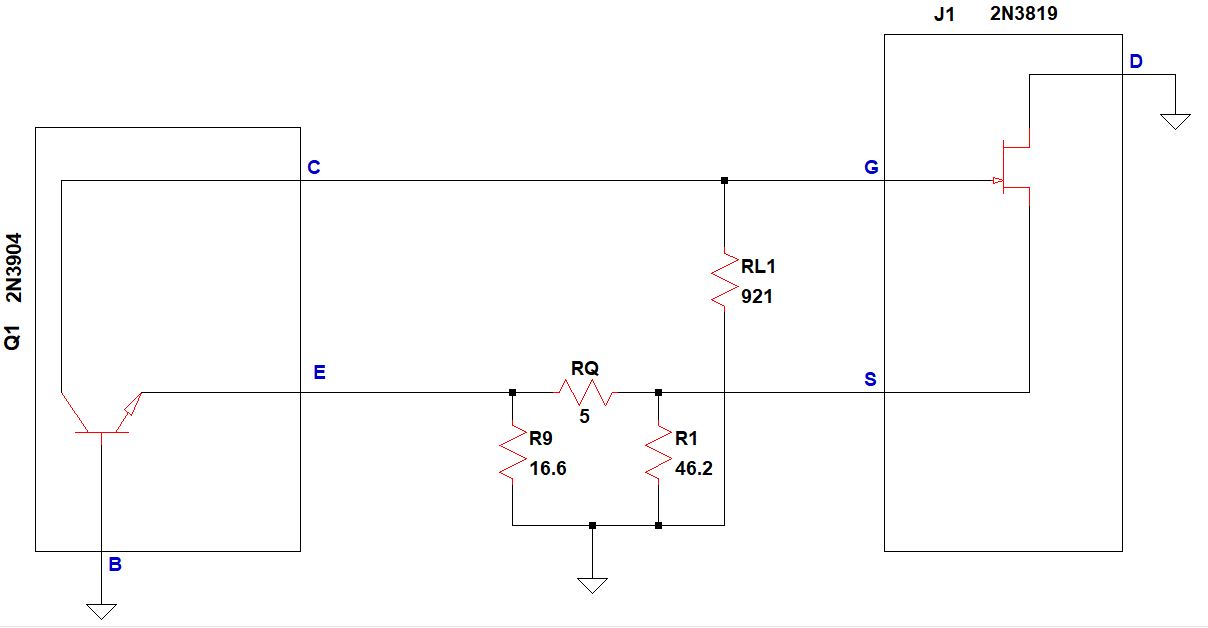
Dove RQ è la resistenza del quarzo.
Il segnale generato, senza alcun carico esterno collegato, è raffigurato nella seguente figura.
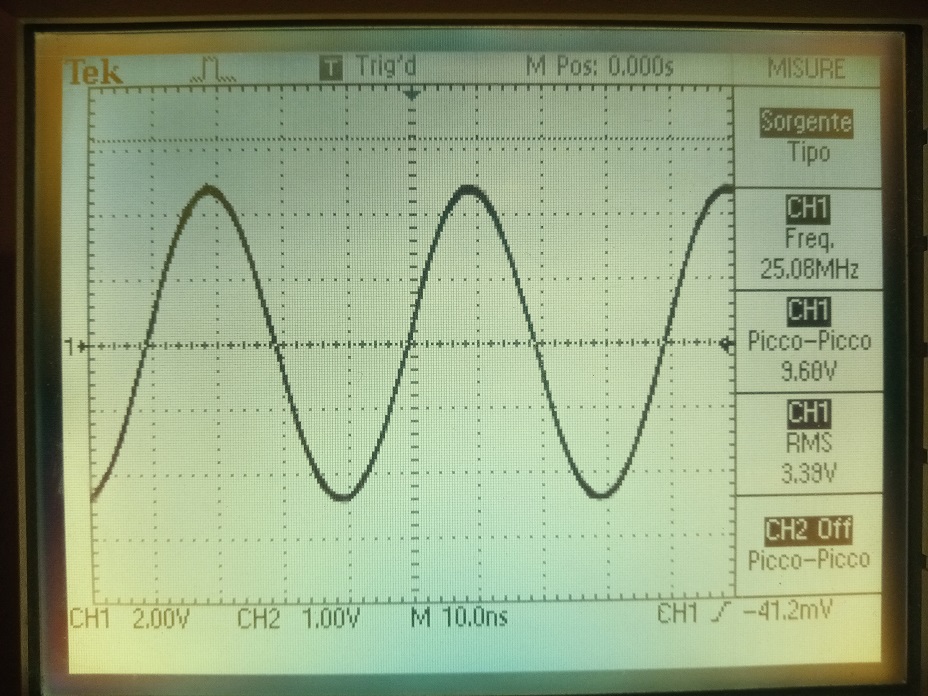
Un circuito semplice che però da ottimi risultati.
Fabio
Ma da quale frequenza iniziano i capricci tra teoria e pratica? Beh, da quando cominciano a farsi sentire gli elementi parassiti di tipo reattivo nei componenti e nei collegamenti, per dare un valore numerico diciamo da 1 MHz in su. Altre volte forme che ci aspettavamo essere sinusoidali hanno in realtà un aspetto orribile, brutte, con andamento inaspettato e condito da strani picchi, non si capisce se ciò sia dovuto ad un mal funzionamento del circuito o dalla sonda rotta, poi spostiamo il coccodrilletto di massa di quest'ultima su un alto punto ed ecco che appare sull'oscilloscopio una bella sinusoide come avrebbe dovuto essere. Questa, e non solo, è l'alta frequenza.
Inoltre consiglio vivamente di non spostare più i componenti sensibili una volta che il circuito funziona bene, può capitare che ci si accorga che il reoforo di un condensatore (del gruppo risonante ad esempio) sia troppo tirato e per paura che si possa rompere lo si saldi in un altro punto dove sia meno stressato. Dopo la modifica è probabile che il circuito non funzioni più.
D'altronde da qualche parte bisogna pur iniziare e la componente analitica di tutto il processo è comunque la parte più indicata per farlo, la premessa sopra serve solo a mettere in guardia i neofiti avventurieri dell'alta frequenza delle possibili delusioni che potrebbero provare una volta data alimentazione al circuito.
L'oscillatore che tratto in questa pagina è del tipo a base comune, lo schema è riportato nella figura seguente.
Le resistenze R7, R8 e R9 servono per polarizzare il transistor Q2 in zona attiva, la resistenza R1 e l'induttanza RFC1 servono per polarizzare il JFET in zona attiva, la RFC deve presentare una alta reattanza alla frequenza di 25 MHz. Il condensatore C4 serve per mettere a massa la base in modo che la connessione del BJT sia, appunto, a base comune, esso deve presentare una bassa reattanza a 25 MHz. Il condensatore C1 serve per evitare che la continua presente sul collettore di Q1 alimenti il gate di J1, esso deve presentare una bassa reattanza a 25 MHz. I condensatori C5 e C3 servono a bypassare l'alimentazione essi devono presentare una bassa reattanza a 25 MHz, questi due condensatori, apparentemente banali, hanno invece una notevole importanza soprattutto quando l'alimentatore non presenta una bassa impedenza a 25 MHz.
L'oscillazione si genera solo a quella frequenza alla quale la tensione presente al collettore del BJT risulta in fase con quella presente al suo emettitore, in tal modo si instaura una retroazione positiva tra ingresso e uscita. Nel nostro caso questo accade solo quando il gruppo L1 C2 ed il quarzo risuonano a 25 MHz. La frequenza di oscillazione è decisa però solo dal quarzo che ha un Q molto più elevato del circuito risonante, quest'ultimo serve solo a presentare al collettore del transistor una impedenza molto alta a fase zero, infatti, se mentre il circuito è in funzione provate a disaccordare il gruppo L1 C2 (di poco se no l'oscillazione scompare) non cambierà la frequenza di oscillazione ma solo il livello del segnale.
Se invece si toglie il quarzo e si collega direttamente il source di J1 all'emettitore di Q2 (tramite condensatore) il circuito oscillerà alla frequenza di risonanza decisa dal gruppo L1 C2.
Il gruppo risonante L1 C2 è del tipo parallelo, per un ottimo Q dovrebbe avere una induttanza piccola e una capacità grande e vedere ai suoi capi una elevata resistenza, l'induttanza non si può però scegliere troppo piccola per evidenti difficoltà costruttive e per evitare che predominino le induttanze distribuite (più difficili da gestire) rispetto a quella concentrata in un punto. Ho scelto un valore di 100nH, un buon compromesso. Nonostante questa scelta le induttanze parassite si fanno sentire tanto che conviene posizionare il condensatore C2 vicinissimo al gate di J1 in modo che possa entrare in risonanza con la complessiva induttanza che vede. Se invece C2 si mettesse vicino a L1 accadrebbe che esso andrebbe in risonanza con la induttanza concentrata e le restanti distribuite rimarrebbero fuori al circuito risonante e si porrebbero lungo il percorso in casuali (dipendendo da come è stato realizzato il circuito) connessioni serie parallelo con conseguenze disastrose per il livello del segnale.
Diversamente dal circuito risonante parallelo quello del quarzo è del tipo serie, per avere un alto Q il quarzo deve vedere una resistenza molto bassa il che è assicurato sia dall'source di J1 che dall'emettitore di Q2, infatti entrambi offrono una resistenza dell'ordine di poche decine di ohm.
Ma entriamo ora nei particolari. Nella figura sottostante è raffigurato il circuito equivalente del circuito per i soli segnali dinamici. Il riquadro attorno a Q2 e a J1 riguarda rispettivamente il transistor ed il JFET vero e proprio con le loro impedenze di ingresso e di uscita, queste le ho ricavate tramite il simulatore LTSpice a 25 MHz quindi il loro valore è approssimato ma sufficientemente vicino alla realtà per quello che serve a noi.
Dove:
RC e CC sono rispettivamente la resistenza e la capacità di uscita del transistor.
RE e CE sono rispettivamente la resistenza e la capacità d'ingresso del transistor.
CGj è la capacità d'ingresso del JFET.
RJ e CSJ sono rispettivamente la resistenza e la capacità di uscita del JFET.
RL1 è la resistenza equivalente parallelo di L1.
RRFC è la resistenza equivalente parallelo della RFC.
Non ho riportato la resistenza di ingresso del JFT perché essendo molto alta può essere trascurata. Non ho riportato neppure l'induttanza RFC1 dato che quest'ultima ha valore (47u) molto più alto rispetto a quello di L1 (100n), a proposito della RFC due parole vanno spese, per determinare il giusto valore ho avvolto qualche spira sul toroide e ho misurato la tensione sul gate del JFET, poi qualche altra spira e ho misurato di nuovo la tensione, se questa era di valore maggiore a quella misurata precedentemente ho seguitato ad avvolgere spire e così via fino a quando il livello di tensione si è stabilizzato. A quel punto ho contato il numero delle spire avvolte e ne ho ricavato il valore induttivo, 6.5 uH (circa 12 spire).
Ovviamente potevo usare, al posto della RFC, una resistenza di pari valore ma ho pensato che sarebbe stato ideale disporre di un toroide per poter adattare un carico di valore a piacimento alla resistenza di uscita complessiva per il massimo trasferimento di potenza.
L'ultima cosa da dire sulle induttanze è che purtroppo a causa dell'effetto pelle e di prossimità la resistenza serie dei conduttori che le compongono non è trascurabile e bisogna tenerne conto trasformandola in resistenza equivalente parallelo, le due resistenze nello schema dinamico sono RL1 per L1 e RRFC per la RFC.
Il gruppo risonante L1C2 allora vede il parallelo di RC, RL1 e RRFC pari a 921 ohm che gli permette di possedere un Q di circa 58:
Per quanto riguarda le capacità CC e CGJ esse vengono inglobate in C2 e vengono a far quindi parte del circuito risonante. A tal proposito queste, quelle parassite assieme alla non precisa realizzazione dell'induttanza L1 più le induttanze parassite che rientrano nel circuito risonante fanno scostare di molto il valore teorico calcolato di C2 che avrebbe dovuto essere circa 405 pF:
I quarzo vede una resistenza complessiva di 62.9 ohm che gli permette di possedere un Q di circa 10000, le capacità CSJ e CE vengono viste dal quarzo in serie e assumono un valore complessivo di circa 0.4 pF che assieme a quelle parassite (di pochi pico) non disturbano affatto il quarzo stesso.
Nella figura sottostante è raffigurato il circuito dinamico in risonanza.
Dove RQ è la resistenza del quarzo.
Il segnale generato, senza alcun carico esterno collegato, è raffigurato nella seguente figura.

Un circuito semplice che però da ottimi risultati.
Fabio