Verifica del 23 aprile 2007 classe II sez. C
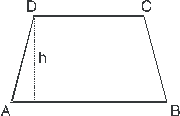
In un trapezio isoscele la somma delle due basi è 704 cm e la differenza è 224 cm, mentre l'altezza è ¾ della semidifferenza delle basi. Calcola area e perimetro del trapezio.

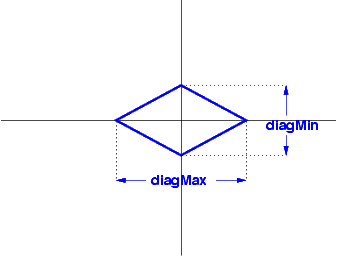
In un rombo l'area è 48600 cm2 e la diagonale minore è 270 cm. Calcola il perimetro del rombo.
Dividere 15625 in parti direttamente proporzionali a 11 e 14.
Dividere 72072 in parti inversamente proporzionali a 3 e 4.
Se con 1 dollaro si acquistano 0,74 euro, con 2379 euro quanti dollari si acquistano?
Svolgimento
(n.b. per questioni tecniche e di tempo abbiamo omesso i disegni delle figure geometriche, che tuttavia nello svolgimento di un compito sono essenziali)
1) Se la differenza delle basi del trapezio è 224cm, allora la semidifferenza è 224:2 = 112 cm, quindi per calcolare l'altezza del trapezio calcolo i ¾ di 112 = 112*3:4 = 84 cm. Poiché l'area del trapezio è data dal prodotto della somma delle basi per l'altezza diviso 2, avremo:
area = (704*84): 2 = 29568 cm2.
Per calcolare il perimetro, trovo prima il lato obliquo col teorema di Pitagora:
lato obliquo = radice quadrata di (112^2 + 842^2) = 140 cm.
Quindi perimetro = somma delle basi + lato obliquo*2 = 704 + 2*140 = 984 cm.
(n.b. abbiamo usato il simbolo A^2 per indicare il quadrato del numero A)
2) Dall'area e dalla diagonale maggiore, con la formula inversa, ricavo la diagonale minore:
d = (A*2):D = (48600*2):270 = 360 cm.
Le due semidiagonali quindi misurano rispettivamente 180 cm (la maggiore) e 135 cm (la minore).
Applicando il teorema di Pitagora calcolo il lato del rombo:
l = radice quadrata di(135^2 + 180^2) = 225 cm.
Da ciò il perimetro = l*4 = 225*4 = 900 cm.
3) Dividere 15625 in parti direttamente proporzionali a 11 e 14
x + y = 15625
x : y = 11 : 14
Applico la proprietà del comporre:
(x +y) : x = (11+14):11
15625 : x = 25 : 11
Da cui x = (15625*11):25 = 6875 e y = 15625 – 6875 = 8750.
4) Dividere 72072 in parti inversamente proporzionali ai numeri 3 e 4
Il problema si riconduce a quello di dividere 72072 in parti direttamente proporzionali a 1/3 e ¼, quindi avremo:
x + y = 72072
x : y = 1/3 : ¼
applicando la proprietà del comporre avremo:
72072 : x = 7/12 : 1/3 da cui x = 72072 * 1/3 * 12/7 = 72072* 4/7 = 41184
Quindi y = 72072 – 41184 = 30888:
5) per ricavare il valore in dollari di 2379€, tenuto conto che si tratta di grandezze direttamente proporzionali, devo risolvere la seguente proporzione:
2379 : x = 0,74 : 1 da cui x = 2379 : 0,74 = 3214,….€
(n.b. abbiamo usato il simbolo * per indicare l'operatore della moltiplicazione)