|
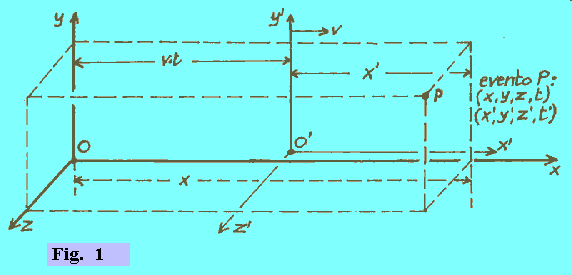
TRASFORMAZIONI GALILEIANE Sono quelle che vengono studiate nell'ambito della fisica classica. Gli eventi (urti tra particelle, accensioni di lampadine, ecc.) avvengono in punti dello spazio e a diversi istanti di tempo. Uno stesso evento può essere studiato da diversi osservatori. Ciascun osservatore registra l'evento rispetto a un suo sistema di riferimento mediante tre coordinate spaziali, x, y, z, e una coordinata temporale t, che ogni osservatore registra con un suo orologio. Consideriamo due osservatori, O e O', con O' che viaggia con velocità costante v rispetto ad O, lungo l'asse comune x-x'. Entrambi gli osservatori sono dotati di metro ed orologio (ovviamente perfettamente identici), in modo che ciascuno possa misurare le coordinate di un evento. Supponiamo inoltre che, nell'istante in cui O' coincide con O, nell'istante del sorpasso, i due orologi siano regolati in modo che t = t' = 0. In queste condizioni, ad un qualsiasi evento P l'osservatore O assegnerà le coordinate x, y, z, t, mentre le coordinate che verranno assegnate da O' saranno x', y', z', t'. |
 |
|
Si tratta dunque, date le coordinate dell'evento P rispetto ad O, x, y, z, t, di trovare le coordinate che saranno misurate simultaneamente da O', x', y', z', t', e viceversa. Si ha subito: x' = x - v•t, y'=y, z' = z, t' = t Per il problema inverso (date le coordinate rispetto ad O', trovare quelle rispetto ad O) si ha: x = x' + v•t', y = y', z = z', t = t' Come si vede, nella fisica classica si assume implicitamente t = t'. (Il lettore noti che l'avverbio "simultaneamente" è stato usato sopra tranquillamente, dando per scontato che esso non ponga particolari problemi). Oltre che studiare le trasformazioni di coordinate, occorre prendere in considerazione anche le trasformazioni di velocità rispetto a due sistemi. Si studia cioè la velocità di una particella osservandola rispetto a due diversi sistemi di riferimento. Indicando con Ux, Uy, Uz le componenti della velocità della particella rispetto al sistema di riferimento di O, e con U'x, U'y, U'z quelle rispetto al sistema di riferimento di O', ammettendo per semplificare che la particella si muova parallelamente all'asse x - x', sempre con velocità costante, v, per passare dall'uno all'altro dei due sistemi si hanno le relazioni seguenti: U'x = Ux - v, U'y = Uy, U'z = Uz Ux = U'x + v, Uy = U'y, Uz = U'z. |
|
I POSTULATI DI EINSTEIN Einstein respinse il concetto newtoniano di tempo assoluto (tempo che "fluisce" in maniera uguale per tutti gli osservatori, comunque in moto). Il suo ragionamento fu più o meno questo: " . . . se si potesse trasmettere istantaneamente a tutti i punti dello spazio l'informazione dell'avvenuta esplosione di due stelle lontanissime l'una dall'altra [cosa possibile solo con velocità infinita della luce], avrebbe senso per tutti gli sperimentatori (comunque in moto l'uno rispetto all'altro) giudicare se le due stelle sono esplose nello stesso istante. Avrebbero senso cioè i concetti di (1) simultaneità assoluta di due eventi, e quindi di (2) tempo assoluto. Siccome la velocità della luce non è infinita, quei due concetti perdono di significato . . .". In conseguenza di quanto sopra, egli enunciò il suo famoso Principio di relatività, da porre alla base della nuova fisica, attraverso questi due assiomi:
|
| Nella fig. 2 è illustrata una situazione che rientra nell'ambito della fisica classica. Da un veicolo a cui è solidale un sistema di riferimento S', che si muove verso destra alla velocità v = 30 m/s rispetto a un altro sistema di riferimento S, viene lanciato un oggetto nella stessa direzione, alla velocità (rispetto ad S') u' = 10 m/s. | 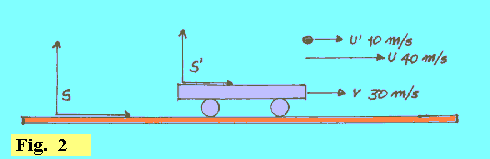 |
| Se ci chiediamo quale sarà la velocità u dell'oggetto rispetto al sistema S, non facciamo altro che applicare le trasformazioni galileiane per le velocità viste sopra, ed avremo: u = u' + v = 10 + 30 = 40 m/s |
| Nella fig. 3 vediamo invece che quando la velocità in gioco è grandissima (in questo caso la velocità della luce, che è la massima velocità materiale possibile), le trasformazioni galileiane non possono più essere applicate: | 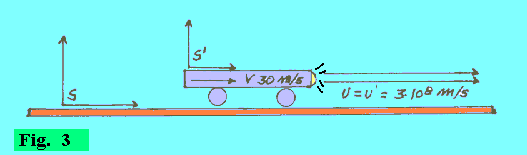 |
| Infatti, in questo caso, rispetto a entrambi i sistemi di riferimento la velocità della luce è la stessa (perfino se il veicolo si muovesse, per assurdo, alla velocità c). | |
| DEFINIZIONE OPERATIVA DEL CONCETTO DI SIMULTANEITA' | |
| Supponiamo che due fenomeni, F1 ed F2, che avvengono nei punti dello spazio P1 e P2, producano entrambi anche l'emissione di un lampo di luce dai due punti negli istanti in cui ciascun fenomeno avviene. Diremo che i due fenomeni sono simultanei se la luce che essi emettono viene percepita nello stesso istante da un osservatore che si trovi in un punto P, equidistante da P1 e P2. | 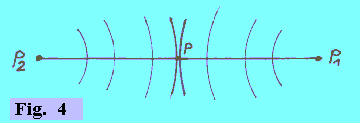 |
|
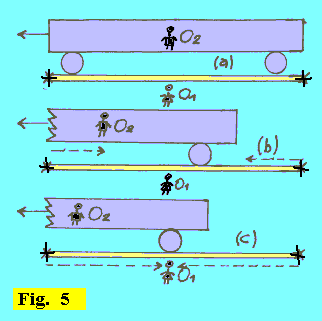
RELATIVITA' DEL GIUDIZIO DI SIMULTANEITA' Vediamo come Einstein, tramite un "Gedankenexperiment" (esperimento ideale), giunge alla conclusione che il giudizio di simultaneità di due eventi è relativo (cioè dipendente dall'osservatore). Immaginiamo che due petardi esplodano sui binari di un treno in corsa, in corrispondenza delle estremità di un lunghissimo vagone, nell'istante in cui un osservatore O1 al suolo, esattamente a metà lunghezza tra i due punti di esplosione, si trova affacciato con un osservatore O2 sul vagone (con "nell'istante in cui un osservatore O1" intendiamo "rispetto al sistema di riferimento di O1"). Questa sarà la situazione (a) della figura 5. Essendo il treno in corsa (velocissima) verso sinistra, il lampo dell'esplosione di sinistra raggiunge l'osservatore O2 prima del lampo dell'esplosione di destra. (Questa è la situazione (b)). In base alla definizione di simultaneità di due eventi data sopra, per O2 è lecito affermare che le due esplosioni non sono state simultanee. Invece O1, essendo posizionato esattamente a metà tra i due punti di esplosione, viene raggiunto dai due lampi contemporaneamente, e quindi conclude che le due esplosioni sono state simultanee.(Situazione (c)). |
 |
|
Dobbiamo quindi ammettere che il giudizio di simultaneità di due eventi non è assoluto, ma relativo: due eventi che sono giudicati simultanei in un certo sistema di riferimento, non lo sono in un altro se tra i due sistemi esiste un moto relativo. Si osservi anche che, dal punto di vista fisico, il sistema di riferimento di O1 non gode di alcun privilegio rispetto a quello di O2. (Nell'esempio appena visto poi, se due altri eventi sono giudicati simultanei nel sistema di O2, non lo saranno certamente nel sistema di O1). | |
Vediamo cosa si intende per "operazione di sincronizzazione di due orologi". Occorre chiarire preliminarmente un concetto. Il valore finito della velocità della luce implica che quando osserviamo l'ora segnata da un orologio, ciò che "vediamo" non è l'ora dell'istante in cui percepiamo il valore dell'orario: noi percepiamo l'orario dell'istante in cui la luce era partita dal quadrante dell'orologio per procedere verso i nostri occhi. Ecco una procedura per la sincronizzazione di due orologi (ovviamente appartenenti allo stesso sistema di riferimento). Dobbiamo disporre di due orologi con queste caratteristiche:
|
|
DILATAZIONE DEL TEMPO CON LA VELOCITA' Per arrivare alla comprensione di quest'altro concetto dobbiamo immaginare un altro esperimento ideale. Abbiamo un razzo che scorre a grande velocità, v, su una piattaforma. All'interno del razzo c'è il sistema di riferimento O1. Solidale alla piattaforma c'è invece il sistema O2. Il fenomeno da studiare avviene all'interno del razzo, ed è costituito da un segnale elettromagnetico che, emesso da un emettitore E, si propaga fino a uno specchio S1, posto a distanza d dall'emettitore, viene da questo riflesso e ritorna all'emettitore (che è anche ricevitore). | 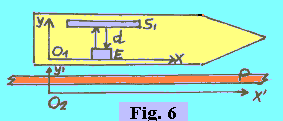 |
|
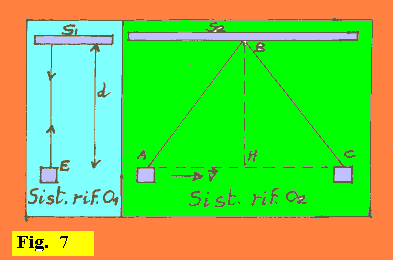
Analizzando il fenomeno rispetto al sistema O1, concludiamo subito dicendo che il tempo impiegato dal segnale per il viaggio di andata ritorno è dato da Dt = 2•d/c, da cui si ha anche: d = 0.5•c•Dt. (Diciamo che il sistema O1 è solidale con il fenomeno, intendendo dire con ciò che le coordinate spaziali del punto di inizio-fenomeno coincidono con quelle del punto di fine-fenomeno. In tal caso il tempo Dt è detto tempo proprio del fenomeno). |
 |
|
Rispetto al sistema di riferimento O2, dobbiamo ammettere che il segnale non ritornerà allo stesso punto dal quale era partito (come all'interno del razzo). Ritornerà in un punto dell'asse x' di O2, tanto più distante dal punto di partenza quanto è maggiore la velocità v del razzo, per cui impiegherà un tempo Dt', sicuramente maggiore di Dt. (Evidentemente, lungo l'asse x' ci dovranno essere tanti ricevitori sincronizzati con l'emettitore, e un ricevitore dovrà proprio essere nel punto di ritorno C. Si noti anche che il sistema O2 non può essere detto solidale con il fenomeno). Dal triangolo ABC, con H punto medio tra A e C, abbiamo subito: AB2 = HB2 + AH2 (1) Indichiamo con:
(Dt')2) = (Dt)2 • [c2 / (c2 - v2)] Possiamo porre: [c2 / (c2 - v2)] = 1/[(c2 - v2)/c2] = 1 / [1 - (v/c)2] per cui: (Dt')2 = (Dt)2 / [1 - (v/c)2] e finalmente: Dt' = Dt • 1 / [1 - (v/c)2]1/2 (2) La quantità 1/[1 - (v/c)2]1/2 si indica di solito con g mentre la quantità v/c si indica di solito con b. La formula (2) ci dice dunque che il tempo di durata di un fenomeno (che avviene nel sistema O1) se misurato dal sistema O2, in moto relativo rispetto ad O1, appare dilatato (Dt' > Dt). Ci dice cioè che la durata di un fenomeno è minima se viene misurata nel sistema di riferimento in cui l'osservatore risulta fermo rispetto al fenomno (Dt per intenderci, che è appunto detto tempo proprio del fenomeno). La formula ci dice infine che (1) per v prossimo a c, tanto g che Dt tendono a valori infinitamente grandi, mentre (2) per v prossimo a zero g tende al valore 1 e Dt' tende a Dt Le formule conclusive sono:
|
|
CONTRAZIONE DELLE LUNGHEZZE CON LA VELOCITA' Studiamo ancora un treno che scorra velocemente a velocità uniforme v su dei binari diritti. Precisamente, ci poniamo il problema di studiare quale differenza trovino due osservatori, l'uno O1 al suolo, l'altro, O2 sul treno, nelle misure che ciascuno di loro esegue della distanza tra due paletti, precedentemente piantati da qualcuno nel terreno, lungo i binari. Evidentemente O1 è in grado di misurare la distanza tra i due paletti, senza tante storie, semplicemente facendo uso di un metro. Troverà per essa il valore Dx, che chiamerà lunghezza propria (perchè essa è solidale (immobile) con il suo sistema di riferimento). Ma questo valore Dx può essere ottenuto da O1 anche in altro modo. Può ottenerlo moltiplicando la velocità del treno, v, per il tempo Dt' che, secondo lui, (cioè con una sua misura), un punto fisso del treno impiega per scorrere tra i due paletti (questo tempo è un tempo dilatato Dt', perchè è misurato da un osservatore (O1), che non è solidale con il movimento). Quindi per O1 la lunghezza tra i paletti è: Dx = v•Dt'. Ora vediamo come O2 può misurare la distanza tra i due paletti. Diciamo subito che per lui il metodo più conveniente è proprio quello di moltiplicare la velocità del treno per il tempo che, secondo lui, un punto fisso del treno impiega per transitare tra i due paletti, e questo sarà dunque un tempo proprio Dt. Quindi, per O2 la distanza sarà: Dx' = v•Dt. Siccome in precedenza avevamo ottenuto che Dt = Dt' • [1 - (v/c)2]1/2, avremo: Dx' = v•Dt = v•Dt'•[1 - (v/c)2]1/2, e siccome sopra abbiamo visto che v•Dt' = Dx, in definitiva avremo: Dx' = Dx • [1 - (v/c)2]1/2 (3) La formula (3) ci dice che una lunghezza (Dx), misurata tra due punti fissi in un sistema di riferimento (O1), è la massima possibile, ed è detta lunghezza propria. Tutte le altre misure tra gli stessi punti, eseguite da sistemi in moto relativo rispetto a quella lunghezza sono minori della Dx, (lunghezze contratte), e la contrazione è tanto maggiore quanto maggiore è la velocità relativa tra i due sistemi. Le formule per le lunghezze sono dunque:
|
|
INVARIANZA DELLA DIMENSIONE PERPENDICOLARE AL MOTO RELATIVO Ci proponiamo ora di dimostrare che la contrazione causata dalla velocità non avviene nella dimensione trasversale dell'oggetto (quella perpendicolare alla direzione in cui si ha il moto relativo). In senso trasversale la dimensione rimane invariata. Consideriamo ancora due sistemi di riferimento, S1 ed S2, con S2 in moto a velocità v rispetto ad S1. Nella fattispecie, S1 è costituito da una galleria ferroviaria, ed S2 da un treno che entra in essa a velocità v (ammettiamo anche che la dimensione trasversale dei vagoni sia soltanto infinitesimamente inferiore a quella della galleria). Dimostreremo che i vagoni non subiscono alcuna alterazione nella loro dimensione trasversale, chiunque sia ad eseguire le misure. Daremo la dimostrazione per assurdo, cioè dimostreremo che si arriva a un'assurdità ammettendo che la dimensione trasversale dei vagoni in corsa subisca alterazioni, in diminuzione o in aumento. Giudichiamo il fenomeno dal punto di vista del sistema S1 (galleria): la galleria è ferma e il treno è in moto a grande velocità. Se ammettiamo per ipotesi che la dimensione trasversale dei vagoni diminuisca con la velocità, il treno scorre nella galleria senza problemi, e tanto più facilmente quanto maggiore è la sua velocità. Ora esaminiamo il fenomeno dal punto di vista del sistema S2 (treno): il treno è fermo e la galleria scorre a grande velocità. Se ammettiamo per ipotesi che la dimensione trasversale della galleria diminuisce al crescere della velocità, questa cessa di scorrere (treno e galleria si incastrano). Si ha un'assurdità perchè non può essere che uno stesso fenomeno avvenga o non avvenga per due osservatori posti in sistemi di riferimento diversi. Allora, siccome ammettere che la dimensione trasversale degli oggetti in movimento diminuisce con la velocità porta a un assurdo, quell'ammissione dev'essere respinta. Allo stesso modo si dimostra che non si può ammettere che la dimensione trasversale degli oggetti in movimento subisca dilatazione. Quindi rimane invariata. |
Sono quelle che sostituiscono le trasformazioni galileiane, che diventano inaccettabili quando si ha a che fare con velocità molto grandi. H. A, Lorentz le sviluppò come quelle che consentivano alle equazioni elettromagnetiche di Maxwell di rimanere invarianti nel passare da un sistema di riferimento a un altro (quando tra i due sistemi esisteva un moto relativo). (Rimanere invarianti significa che le equazioni dovevano godere della proprietà di mantenere la stessa forma nei due sistemi). Anche queste tasformazioni, come quelle galileiane, consentono di passare dalle coordinate di un evento rispetto a un sistema, a quelle dello stesso evento, rispetto a un altro sistema, in moto rispetto al primo. Date dunque le coordinate di un evento x, y, z, t, rispetto al sistema di riferimento O, le coordinate x', y', z', t' rispetto al sistema O' (in moto rispetto al sistema O alla velocità v lungo l'asse comune x-x'), si ottengono da: (ci si riferisca ancora alla figura 1) x' = (x - v•t) / [1 - (v/c)2]1/2, y' = y, z' = z, t' = (t - v•x/c2) / [1 - (v/c)2]1/2 Date invece le coodinate x', y', z', t',, rispetto ad O', le coordinate x, y, z, t si ottengono da: x = (x' + v•t') / [1 - (v/c)2]1/2, y = y', z = z', t = (t' + v•x'/c2) / [1 - (v/c)2]1/2. Come si vede, ogni sistema di riferimento ha una sua coordinata tempo. Soltanto quando tra due sistemi di riferimento il moto relativo è nullo si ha la coincidenza delle due coordinate tempo. |
|
L'ETERE Sappiamo che le onde sonore si propagano nell'aria, nell'acqua e nei solidi. Necessitano di un mezzo materiale per la propagazione. Non possono propagarsi nel vuoto. Ciò indusse i fisici della fine del secolo XIX a pensare che anche le onde elettomagnetiche necessitassero di un mezzo di propagazione. Questo mezzo fu postulato nell'etere. Si ammetteva che l'etere doveva riempire tutto l'universo, quindi anche lo spazio intraatomico e interatomico. Poi doveva possedere altre qualità: essere completamente trasparente alla luce (nessun assorbimento di luce), doveva avere massa e viscosità nulle, ma nello stesso tempo avere massima elasticità. Il successo della teoria della relatività ristretta decretò l' inutilità e quindi la cessazione di significato fisico dell'etere. |
|
INVARIANZA DELLA DISTANZA RISPETTO AL SISTEMA DI RIFERIMENTO A partire dai due assiomi di Einstein e stabilito che:
|
|
| Definiamo analiticamente evento la quaterna di coordinate (x, y, z, t) rispetto a un certo sistema di riferimento. Nella figura 8 i due punti O e O' appaiono distinti, ma dobbiamo pensarli coincidenti. Sono stati posti separati unicamente per rendere chiaro al lettore che si ha a che fare con due sistemi di riferimento diversi. I due segmenti DS devono dunque essere pensati coincidenti. | 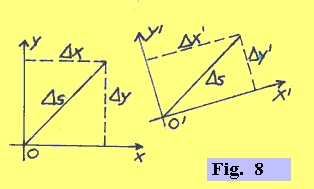 |
|
Dati dunque due sistemi di riferimento distinti, uno stesso spostamento DS, pur essendo descritto in ogni sistema da componenti diverse, è invariante da un sistema all'altro. Infatti, si ha: [(Dx)2 + (Dy)2]1/2 = [(Dx')2 + (Dy')2]1/2 = . . . . . . = DS (invariante, riferito allo spostamento tra due punti dello spazio, significa indipendente dal sistema di riferimento, che viene scelto arbitrariamente per dare le coordinate dei due punti). Da quanto sopra emerge che la descrizione dello spazio tramite tre assi cartesiani arbitrariamente scelti dall'osservatore non ha alcna rilevanza fisica. Ciò che invece ha significato fisico è:
| |
|
L'INTERVALLO INVARIANTE Diamo ora la definizione analitica di intervallo invariante. In seguito vedremo il suo significato fisico. Dati due eventi (ad esempio l'accensione di due lampadine), separati dalle differenze di coordinate Dx, Dy, Dz, Dt, definiamo intervallo invariante (o semplicemente intervallo) tra i due eventi la quantità Ds, (delta sigma), data da: Ds = [ (c•Dt)2 - (Dx)2 - (Dy)2 - (Dz)2 ]1/2 (1) L'espressione (1) diventa molto semplice quando il fenomeno avviene solidalmente con il sistema di riferimento. In tal caso la durata del fenomeno è pari al tempo proprio Dt, per cui, essendo al contempo Dx = Dy =Dz = 0, si ha semplicemente: Ds = Dt (2) |
|
LO SPAZIO-TEMPO Prima dell'introduzione della relatività ci si riferiva comunemente al concetto di spazio secondo una visione euclidea. Per spazio si intendeva quello euclideo, piatto, a tre dimensioni. Euclideo nel senso di quello che garantisce la validità del V postulato di Euclide, (quello della unicità della parallela a una retta data, per un punto dato), e piatto perchè tale da consentire che la somma degli angoli del triangolo che nasce dalla congiunzione di tre suoi punti qualsiasi, sia esattamente un angolo piatto. La relatività considera invece il concetto di spazio-tempo. Lo spazio-tempo nel quale valgono la (1) e la (2) è gestibile per mezzo di una speciale geometria (che non è la ordinaria euclidea), ma quella investigata da H. Minkovsky (insegnante di Einstein al Politecnico di Zurigo), che nei primi anni del secolo scorso introdusse il concetto di spazio-tempo. Questo nuovo ente, detto anche spazio di Minkovsky, richiedeva quattro dimensioni, tre spaziali e una temporale, perchè esso era costituito di eventi (e non di punti come lo spazio euclideo), e abbiamo visto che l'evento richiede anche una dimensione temporale. Vedremo che lo spazio-tempo ha proprietà diverse da quelle dello spazio euclideo. La tabella che segue fornisce l'espression dell'intervallo invariante per ogni tipo di spazio. |
| |||||||||||||||||||||||||
|
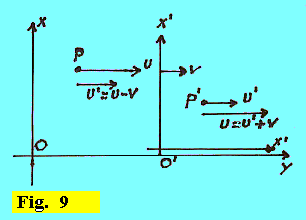
COMPOSIZIONE DELLE VELOCITA' Per le trasformazioni di Galileo, abbiamo visto che se una particella materiale P ha velocità u rispetto al sistema di riferimento O, allora se il sistema O' ha velocità v rispetto ad O (sempre diretta secondo gli assi comuni x-x'), la particella rispetto ad O' avrà velocità u', tale che u' = u - v. Inversamente sarà u = u' + v (per una particella materiale P' che abbia velocità u' rispetto al sistema O'). Nella teoria della r. r., le formule di cui sopra non sono valide e devono essere sostituite dalle seguenti: u' = (u - v) / (1 - u•v/c2) e u = (u' + v) / (1 + u'•v/c2). |
 |
|
Vediamo se queste formule che abbiamo appena dato rispettano il postulato di Einstein, per il quale la velocià della luce nel vuoto deve sempre avere valore c per qualunque sistema di riferimento. Supponiamo di avere un fotone che nel sistema S abbia velocità u = c. Ci domandiamo quale sarà la sua velocità u' nel sistema S', in moto rispetto ad S alla velocità v. Applicando le formule di cui sopra, avremo: u' = (u - v) / (1 - u•v/c2) = (c - v) / (1 - c•v/c2) = (c - v) / (1 - v/c) = (c - v) / (c - v)/c = c Vediamo dunque che in entambi i sistemi la velocità del fotone è sempre c, e questo qualunque sia la velocità relativa v tra i due sistemi (perfino anche se v = c). |
|
EQUIVALENZA TRA MASSA ED ENERGIA Secondo la teoria della relatività, se un corpo assorbe la quantità di energia E, la sua massa aumenta della quantità Dm, tale che Dm = E/c2. Se invece un corpo emette energia (per esempio, emettendo luce) la sua massa diminuisce. Mentre per la meccanica classica le due leggi della conservazione dell'energia e della conservazione della massa sono due leggi indipendenti, in meccanica relativistica le due grandezze, massa ed energia, non sono separate: in questo ambito la massa è una forma di energia. |
|
INTERCAMBIABILITA' TRA MASSA ED ENERGIA L'equazione Dm = E/c2 e opportune verifiche sperimentali permettono di affermare che la massa è una forma di energia, perchè anche sottraendo energia a un corpo scompare della massa. Tutte le trasformazioni di massa in energia e viceversa sono regolate dalla relazione di Einstein che, di solito, è scritta nella forma: E = m•c2. In particolare, un corpo fermo in un certo sistema di riferimento, in quella situazione possiede energia E0 = m0•c2, detta energia di riposo, mentre m0, massa a velocità zero, è detta massa di riposo. |
|
ENERGIA TOTALE RELATIVISTICA Consideriamo un corpo qualsiasi in condizioni di riposo in un certo sistema. Abbiamo visto che la sua energia di riposo è data da: E0 = m0•c2. Secondo la fisica classica, avevamo a suo tempo studiato che esso, a velocità v, possedeva energia cinetica K data da: K = 0.5•m0•v2. Allora possiamo modificare la formula che avevamo appreso a suo tempo nella fisica classica e dire che, in quell'ambito, cioè per v molto minore di c (si scrive v << c), alla velocità v, la sua energia totale Et, è data da: Et = m0•c2 + 0.5•m0•v2. In definitiva si ha: Et = m0•c2 • [1 + 0.5•(v/c)2]. |
|
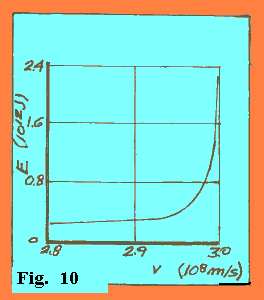
Siccome per v << c si ha praticamente [1 + 0.5•(v/c)2] = 1 / [1 - (v/c)2]1/2, possiamo dire che nell'ambito della fisica classica, cioè a basse velocità, (v << c), si ha: Et = m0•c2 / [1 - (v/c)2]1/2. La figura 10 mostra l'andamento dell'energia totale di un elettrone in funzione della sua velocità v. Quando la velocità diventa molto prossima a c, l'energia totale dell'elettrone cresce senza limiti. Il fatto che per v = c ci sia un asintoto indica che al tendere di v a c, E tende a diventare infinitamente grande, cioè per accelerare un corpo fino alla velocità c ci vuole un’energia impossibile da realizzare. Quindi c è una velocità limite. |
 |
|
MASSA RELATIVISTICA E’ data da: mr = m0 / [1 - (v/c)2]1/2 Quindi la massa relativistica di un corpo, non è una quantità costante come m0, ma è funzione della sua velocità. Per v = 0 si ha mr = m0 |
|
QUANTITA’ DI MOTO RELATIVISTICA Nella meccanica classica avevamo appreso che la quantità di moto, p, di un corpo è quella grandezza data dal prodotto della massa del corpo per la sua velocità. Avevamo cioè p = m0•v. Definiamo quantità di moto relativistica , pr, di un corpo di massa relativistica mr, in moto a velocità v, la quantità pr = mr• v = m0 • g • v Ancora, per v << c si ha: pr = m0 • v = p, cioè la quantità di moto della meccanica classica. |
|
QUADRIVETTORE ENERGIA-QUANTITA’ DI MOTO (ENERMOTO) Si dimostra che per un corpo che abbia massa di riposo m0 e velocità v, la quantità E/c e le tre componenti della quantità di moto prlungo i tre assi spaziali, possono essere considerate come le quattro componenti, una temporale e tre spaziali, di un vettore quadridimensionale dello spazio-tempo, detto quadrivettore enermoto, o semplicemente enermoto (con E/c componente temporale e prx, pry, prz le tre componenti spaziali della quantità di moto pr). Se assumiamo v parallelo all'asse x, in modo che sia prx = pr e pry = prz = 0, otteniamo che il modulo del quadrivettore enermoto è dato da: (E/c)2 - (pr)2 = (g•m0•c)2 - (g•m0•v)2 = g•m0•(c2 - v2) = (m0)2•c2. Concludiamo allora dicendo che anche il modulo (la lunghezza) nello spazio-tempo del vettore enermoto è una quantità invariante perché è proporzionale a una quantità invariante del corpo: la sua massa di riposo. |
|
EFFETTO DOPPLER RELATIVISTICO Ricordiamo che , quando nella meccanica classica viene trattato l'effetto Doppler, ci si limita a considerare il caso acustico. In questo ambito, il fenomeno consiste nel fatto che, esistendo un moto relativo tra una sorgente sonora e un ricevitore del suono, la frequenza del suono ricevuto in fase di avvicinamento relativo è diversa dalla frequenza del suono ricevuto in fase di allontanamento. Allora risulta necessario studiare il fenomeno nei due casi:
Siccome le onde luminose non necessitano, come abbiamo visto, di un mezzo materiale per la propagazione, non si ha ragione di studiare l'effetto Doppler nei due casi, come è stato fatto per il suono. |
|
EFFETTO DOPPLER PER LA LUCE Abbiamo un segnale luminoso che viene emesso a frequenza f dalla sorgente S, ed è ricevuto a frequenza f’ dall'apparato ricevitore R, perché tra S ed R esiste moto con velocità relativa di valore v. Se S e R si allontanano, allora, essendo b = v/c, si ha: f’ = f • [(1 - b) / (1 + b)]1/2, quindi f’ < f , cioè la frequenza di ricezione, inferiore a quella di emissione, è spostata verso il rosso (redshift). Se invece S e R si avvicinano, allora si ha: f’ = f • [(1 + b) / (1 - b)]1/2, per cui sarà f’ > f, e quindi la frequenza di ricezione risulterà spostata verso il violetto (blueshift). (Ricordiamo che rappresentando lo spettro delle frequenze delle onde elettromagnetiche con frequenze crescenti da sinistra verso destra, all'estremità sinistra c'è l'infrarosso, all'estremità destra l'ultravioletto). |
|
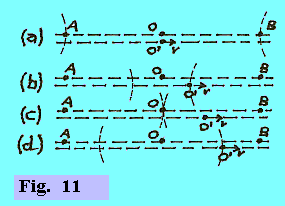
Esercizio 1 - Una lampada a flash (molto potente) è posta nel punto A a 60 Km da un osservatore O. La lampada viene accesa e l’osservatore O vede il flash alle ore 13h 00m 00s. Calcolare l'istante effettivo in cui la lampada è stata accesa (per la costante c assumere sempre il valore 3•108 m/s, anche nei problemi che seguono). Il tempo impiegato dalla luce per percorrere la distanza di 60 Km, da A a O, è dato da: Dt = 60 Km / c = (6•104 m) / ( 3•108 m/s) = 2 • 10-4 s. La lampada è stata accesa 2/10000 di secondo prima delle ore 13. Esercizio 2 - Due eventi (del tipo lampi di luce) si verificano nei punti A e B, posti ad eguali distanze da un osservatore O. Supponiamo che O, per valutare la simultaneità o meno dei due eventi, adotti il seguente criterio: "Per me i due eventi sono simultanei se i segnali luminosi emessi da ciascun evento mi raggiungono in quello che io giudico lo stesso istante“. Mostrare (con l'ausilio di disegni elementari) che, in base a questa definizione, se l’osservatore O rileva che i due eventi sono simultanei, un altro osservatore O’ (che utilizzi lo stesso criterio di simultaneità), in moto relativo rispetto ad O con velocità v, rileverà in generale che i due eventi non sono simultanei (il moto di O' rispetto ad O è tale che esso transita all'altezza di O, con moto verso destra, nell'istante in cui i due eventi si producono in A e B). |
|
- In (a) si vede che nell’istante in cui O’ transita all’altezza di O, due segnali partono dai punti A e B, equidistanti da O (e quindi anche da O’ in quell’istante). - In (b) si vede che il segnale partito da B ha raggiunto O’ (che gli è andato incontro alla velocità v), ma non O. - In (c) si vede che i due segnali hanno raggiunto contemporaneamente O. - In (d) si vede che O’ viene raggiunto anche dal segnale partito da A. Quindi, applicando i due osservatori lo stesso criterio di simultaneità, mentre O può dire che per lui i due eventi sono stati simultanei, O' afferma che per lui non lo sono stati. |
 |
|
Esercizio 3 - Calcolare [1 - (v/c)2]1/2 per: (a) v = 10-2•c e (b) v = 0.9998•c (a) [1 - (v/c)2]1/2 = =  = == [1 - (10-2)2]1/2 = [1 - 10-4]1/2 = [1 - 0.0001]1/2 = 0.99991/2 = 0.9999499 @ 0.99995 (b) [1 - (v/c)2]1/2 = = 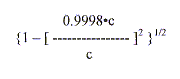 = == [1 - 0.99982]1/2 = [1 - 0.9996]1/2 = [4 • 10-4]1/2 = 0.0199989 @ 0.02. Esercizio 4 - L'osservatore O rileva che il lampo di un flash si è verificato (rispetto al suo sistema di coordinate) nella posizione: x = 100 Km, y = 10 Km, z = 1 Km, all’istante t = 5•10-4 s. Calcolare quali sono le coordinate x’, y’, z’ e t’ dello stesso evento che vengono determinate da un secondo osservatore O’, in moto relativo rispetto ad O, con una velocità v = -0.8•c, nella direzione dell’asse comune x-x’ (come al solito, si supponga che all’istante t = t’ = 0 le origini dei due sistemi coincidevano). |
|
Essere la velocità relativa tra O e O' negativa, significa che essa è diretta verso l'asse negativo di x-x', per cui all’istante t = 5•10-4 s l’origine di O’ sarà a sinistra dell’origine di O. Quindi la figura 12 sarà la rappresentazione della situazione cinematica a quell’istante. |
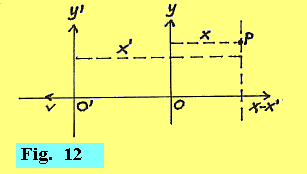 |
Le coordinate simultanee dell’evento, x’, y’, z’, t’, rispetto ad O’, saranno date da: |
|
Esercizio 5 - Si hanno gli eventi A e B. L'osservatore O', in moto rispetto all'osservatore O alla velocità v, rileva tra i due eventi l'intervallo temporale t'B - t'A. Applicando le trasformazioni di Lorentz, calcolare quale sarà l'espressione della differenza temporale ricavata dall'osservatore O. Evidentemente, l'osservatore O misurerà la differenza temporale tB - tA. Ecco come si ricava. Per la trasformazione di Lorentz, tB sarà dato da: 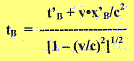 . .Per la stessa trasformazione, tA sarà dato da: 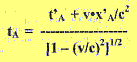 . .Allora avremo: 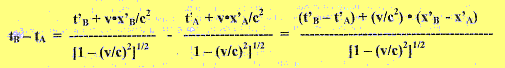 |
|
Esercizio 6 - Risolvere il problema inverso rispetto all'esercizio precedente. Cioè ricavare quale sarà l'espressione della differenza temporale tra i due eventi, misurata dall'osservatore O' (sempre in moto rispetto ad O alla velocità v), essendo tB - tA l'intervallo temporale misurato da O. Ancora, O' misurerà l'intervallo t'B - t'A. Ecco come la ricaviamo. Secondo le trasformazioni di Lorentz, si ha: 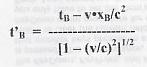 e e 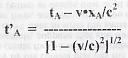 , per cui avremo: , per cui avremo: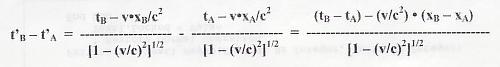 |
|
Esercizio 7 - Dunque, nella fisica relativistica, due eventi che siano simultanei per un osservatore, non lo sono per un altro in moto rispetto al primo. Allora, dati due eventi simultanei per un osservatore O' (in moto), ricavare l'espressione (di tB - tA) che dà l'intervallo temporale tra i due eventi, per un osservatore O, fermo rispetto ad O'. Evidentemente, nella formula: tB - tA = [(t'B - t'A) + (v/c2) • (x'B - x'A)] / [1 - (v/c)2)]1/2 non facciamo altro che porre t'B - t'A = 0, per cui la formula diventa: tB - tA = [(v/c2) • (x'B - x'A)] / [1 - (v/c)2]1/2 |
|
Esercizio 8 - Risolvere il problema speculare a quello dell'esercizio precedente, cioè trovare l'espressione di t'B - t'A, per il caso in cui i due eventi siano simultanei per l'osservatore fermo. Ponendo tB - tA = 0 nella formula ricavata nell'esercizio 6, si ha t'B - t'A = - [(v/c2) • (xB - xA)] / [1 - (v/c)2]1/2 |
|
Esercizio 9 - Un treno lungo 500 m (secondo le misure di un osservatore a bordo) viaggia a una velocità di 100 Km/h. Due lampi colpiscono le estremità del treno simultaneamente (secondo un osservatore a terra). Qual’è la separazione temporale tra i due eventi come risulterebbe misurata da un osservatore sul treno, posto esattamente a metà lunghezza del treno ? Calcoliamo la velocità del treno in m/s. 100.000 : 3600 = X : 1, da cui X = 27.78 m/s Chiamiamo A l'evento che si verifica in corrispondenza della coda del treno, e B quello che si verifica in corrispondenza della testa. Sappiamo già che la differenza t'B - t'A dovrà risultare negativa perchè il lampo relativo all'evento di testa raggiungerà l'osservatore a metà treno prima del lampo relativo all'evento di coda. Consideriamo la formula: tB - tA = [(t'B - t'A) + (v/c2) • (x'B - x'A)] / [1 - (v/c)2]1/2. In essa sono noti: x'B - x'A = 500 m e tB - tA = 0. Possiamo allora ricavare t'B - t'A. Avremo: t'B - t'A = - [(v/c2) • (x'B - x'A)] = - [27.78 m/s /(3•108)2 m/s] • 500 m = - 1.54 • 10-13 s Il segno meno del risultato indica, come abbiamo sopra indicato, che (per l'osservatore a bordo del treno) l'evento B si verifica prima dell'evento A. |
|
Esercizio 10 - Secondo un osservatore O due eventi, 1 e 2, sono separati nello spazio di 600 m e nel tempo di 8•10-7s. Si domanda con quale velocità un osservatore O' si deve muovere rispetto ad O, affinchè per lui i due eventi risultino simultanei. Nella formula: t'2 - t'1 = [(t2 - t1) - (v/c2) • (x2 - x1)] / [1 - (v/c)2]1/2 in cui x2 - x1 = 600 m e t2 - t1 = 8•10-7 s, imponiamo che sia t'2 - t'1 = O. Allora, moltiplicando ambo i membri per [1 - (v/c)2]1/2, otteniamo: 0 = 8•10-7 s - (v/c)•600/(3•108 m/s), da cui v/c = (8•10-7) / (2•10-6) = 0.4. Quindi la velocità di O' dev'essere v = 0.4•c. |
|
Esercizio 11 - L'osservatore O misura le seguenti coordinate dei due eventi 1 e 2: x1 = 6•10-4 m, y1 = z1 = 0, t1 = 2•10-4 s x2 = 12•10-4 m, y2 = z2 = 0, t2 = 1•10-4 s Calcolare con quale velocità l'osservarore O' deve muoversi (lungo l'asse x-x') rispetto ad O, affinchè i due eventi risultino per lui (O') simultanei. Abbiamo la solita espressione: t'2 - t'1 = [(t2 - t1) - (v/c2) • (x2 - x1)] / [1 - (v/c)2]1/2 Essendo; t2 - t1 = 1•10-4 - 2•10-4 = -1•10-4, x2 - x1 = 12•104 - 6•104 = 6•104 e imponendo il problema che t'2 - t'1 = 0, si ha: 0 = (-1•10-4 s) - [(v/c)•(6•104 m)] / (3•108 m/s) da cui: v/c = (-1•10-4) / [6•104 / (3•108)] = -0.5. Il segno meno indica che O' dovrà muoversi lungo l'asse negativo x-x'. |
| Esercizio 12 - Si abbia una riga, (le cui estremità siano A e B), orientata secondo l'asse x-x' e solidale con l'osservatore O' nel senso che, nell'istante t = t' = 0 in cui l'osservatore O' transita alla velocità v per l'origine, anche lo zero della graduazione della riga (estremità A) transiti per l'origine. | 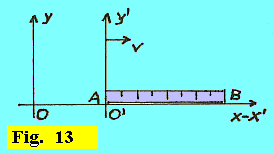 |
Applicando le trasformazioni di Lorentz per la coordinata x, si ha: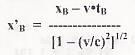 e e 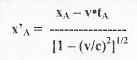 dalle quali si ricava; 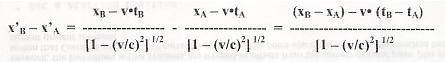 . .Ricavare da quanto sopra la relazione tra lunghezza propria, L0, e lunghezza contratta, L, della riga. La lunghezza propria, L0, quella che l'osservatore O', solidale con il moto della riga, non ha nessuna difficoltà a misurare, è x'B - x'A. La lunghezza contratta L, invece, è quella, xB - xA, che presenta enormi difficoltà ad essere misurata da parte dell'osservatore O. E le difficoltà sono date, come è noto, dal riuscire a rilevare i due valori di xB e di xA nello stesso istante (per O), cioè per tB - tA = 0. Ammettendo che l'osservatore O ci riesca, per vedere la relazione tra L ed l0, nella formula originale si deve porre tB - tA = 0, per cui si avrà: L0 = L / [1 - (v/c)2]1/2 e L = L0 • [1 - (v/c)2]1/2 |
|
Esercizio 13 - Calcolare la contrazione relativistica subita dal diametro della Terra, a causa del suo moto lungo l'eclittica, così come verrebbe misurata da un osservatore O fermo rispetto al Sole. Si assuma quale diametro della Terra a riposo il valore D0 = 1.26•107 m e per velocità della Terra sull'eclittica il valore v = 3•104 m/s. La contrazione relativistica sarà data da D0 - D, cioè da: D0 - D = D0 - D0•[1 - (v/c)2]1/2 = 1.26•107 m - 1.26•107 m • [1 - (3•104)2 m/s / (3•108)2 m/s]1/2 = 1.26•107 m - 1.26•107 m • [1 - 10-8]1/2 = 0.063 m = 63 millimetri. |
|
Esercizio 14 - Un cubo ha un volume, (proprio), V0 = 1000 cm3. Trovare il volume determinato da un osservatore O' che si muove ad una velocità v = 0.8•c rispetto al cubo, in una direzione parallela ad uno dei suoi spigoli. La lunghezza propria dello spigolo del cubo, L0, è data da: L0 = [V0]1/3 = [0.001 m3]1/3 = 0.1 m. La lunghezza contratta dello spigolo, L, per l'osservatore O', risulta da: L = L0 • [1 - (v/c)2]1/2 = 0.1 m • [1 - 0.82]1/2 = 0.1 m • 0.6 = 0.06 m. Le lunghezze degli altri spigoli rimangono invariate per l'osservatore O' perchè essi hanno direzione perpendicolare al moto. Quindi, per O' il cubo diventa un parallelepipedo di lati 0.1 m, 0.1 m e 0.06 m, per cui per O' il volume diventa: V = 0.1 m • 0.1 m • 0.06 m = 0.0006 m3 = 600 cm3. |
|
Esercizio 15 - Ricordiamo le espressioni per rispettivamente il tempo dilatato e il tempo proprio: Dt = Dt0 / [1 - (v/c)2]1/2 e Dt0 = Dt • [1 - (v/c)2]1/2. Abbiamo un aereo che si muove rispetto al suolo alla velocità di 600 m/s. Quanto tempo dovrà trascorrere (secondo misure di orologi di terra) affinchè gli orologi di bordo rimangano indietro di 2 microsecondi rispetto a quelli di terra? Rimanere indietro di 2 microsecondi, significa che dopo un certo tempo di terra dilatato Dt, l'intervallo proprio trascorso a bordo Dt0 è inferiore di 2 microsecondi, cioè che è : Dt - Dt0 = 2•10-6 s. Perchè ciò avvenga, si dovrà avere: Dt = Dt0 / [1 - (v/c)2]1/2 = (Dt - 2•10-6 s) / [1 - (6•102/3•108)2 m/s]1/2 = (Dt - 2•10-6 s) / [1 - 4•10-12]1/2 Ricordiamo che per x molto piccolo si ha: (1 - x)1/2 @ 1 - 0.5•x, e quindi [1 - 4•10-12]1/2 @ 1 - 2•10-12, per cui avremo: Dt = (Dt - 2•10-6) / (1 - 2•10-12) cioè Dt - 2•Dt•10-12 = Dt - 2•10-6 da cui finalmente Dt = 10-6/10-12 s = 106 secondi = circa 11.6 giorni |
|
Esercizio 16 - Calcolare a quale velocità dovrebbe viaggiare un'astronave per consentire a un suo passeggero che ha a disposizione 60 anni da vivere, di raggiungere una galassia distante 160.000 anni luce. I termini del problema e la formula Dt = Dt0 / [1 - (v/c)2]1/2, ci consentono di impostare la relazione: 1.6•104 = 6•10 / [1 - (v/c)2]1/2. Da essa otteniamo questi successivi passaggi: [1 - (v/c)2]1/2 = 3.75•10-4 (v/c)2 = 1 - (3.75•10-4)2 v/c = [1 - (3.75•10-4)2]1/2 Ricordando che per x molto piccolo si ha [1 - x]1/2 @ 1 - 0.5•x, si ha: v/c = 1 - 0.5•(14.0625•10-8) v/c = 1 - 0.703•10-7. |
|
Esercizio 17 - Una riga graduata ha lunghezza a riposo L0 = 1 m, è disposta lungo l'asse x-x' e si muove con una velocità v = 0.6•c rispetto a un osservatore O, lungo il detto asse. Quanto tempo impiegherà la riga ad oltrepassare l'osservatore O? La lunghezza contratta del metro dovuta al moto, L, è data da: L = L0 • [1 - (v/c)2]1/2 = 1 m•[1 - 0.62]1/2 = 0.8 m. Affinchè l’osservatore, fermo rispetto al metro, venga sorpassato dall'intera riga dovrà trascorrere un tempo t dato da t = 0.8 / v = 0.8 / (0.6•3•108 m/s) = 4.44•10-9 s. |
|
Esercizio 18 - Si supponga che un mesone, che venga generato all'altezza dal suolo di 6000 m, abbia tempo di vita medio (tempo proprio) Dt0 = 2•10-6 s, e che si precipiti verso il suolo alla velocità v = 0.998•c. Determinare se esso riesce a raggiungere il suolo prima di decadere, sia secondo la meccanica classica che quella relativistica. Vediamo prima cosa succede secondo la meccanica classica. La distanza che esso è in grado di percorrere è data da: d = v•Dt0 = 0.998•c m/s • 2•10-6 s = 598.8 m Quindi, secondo la meccanica classica il mesone non sarebbe in grado di raggiungere il suolo. Vediamo ora cosa succede secondo la meccanica relativistica. Rispetto a un osservatore al suolo, il tempo di vita medio del mesone risulta dilatato al valore Dt dato da: Dt = Dt0 / [1 - (v/c)2]1/2 = 2•10-6 s / [1 - 0.9982]1/2 = 3.16•10-5 s La distanza percorsa in questo tempo sarà: dsuolo = v•Dt = 0.998•3•108 m/s • 3.16•10-5 s = 9470 m. Quindi il mesone raggiungerà effettivamente il suolo. |
|
Esercizio 19 - Il pilota di una nave spaziale, nel transitare in vicinanza della Terra alla velocità v = 0.6•c, regola il suo orologio sul tempo terrestre (UT), alle ore 00h 00m.
Alle ore 00h 30m (suo orologio) transita in prossimità di una stazione spaziale ferma rispetto alla Terra. Si domanda che ore sono in quel momento sulla stazione spaziale e a Terra. Determinare inoltre quale è la distanza tra la Terra e la stazione spaziale secondo le misure eseguite: (1) dal pilota della stazione spaziale (2) da un osservatore a Terra. Per il pilota l'intervallo trascorso di 30m è un intervallo proprio Dt0. Sulla piattaforma e a Terra, invece, è trascorso un intervallo dilatato Dt, dato da: Dt = Dt0 / [1 - (v/c)2]1/2 = 30•60 s / [1 - 0.62]1/2 = 37.5 minuti Quindi gli orologi della stazione spaziale e di Terra (UT) segnano l'orario: 00h 37m 30s Distanza (1) = 0.6•3•108 m/s • 30•60 s = 3.24•1011 m Distanza (2) = 0.6•3•108 m/s • 37.5•60 s = 4.05•1011 m. |
|
Esercizio 20 - L'osservatore O rileva due eventi distanziati nello spazio xB - xA = 3.6•108 m e nel tempo tB - tA = 2 s. Qual'è l'intervallo di tempo proprio Dt0 che intercorre tra i due eventi? L'intervallo rilevato da O non è intervallo di tempo proprio perchè egli ha misurato tra i due eventi un intervallo spaziale diverso da zero. Tra i due eventi, invece, rileverà il tempo proprio Dt0 soltanto quell'osservatore O' che viaggi tra essi alla velocità v tale da far risultare x'B - x'A = 0. Allora avremo: x'B - x'A = [(xB - xA) - v•(tB - tA)] / [1 - (v/c)2]1/2 da cui: 0 = [3.6•108 m - v•2 m] / [1 - (v/c)2]1/2, che risolta rispetto a v dà: v = 1.8•108 m/s e v/c = 0.6. Ora, dalla formula: t'B - t'A = [(tB - tA) - (v/c2)•(xB - xA)] / [1 - (v/c)2]1/2 sostituendo tutti i termini noti si ha: Dt0 = t'B - t'A = [2 s - 0.6/(3•108 m/s)•(3.6•108 m/s)] / [1 - 0.62]1/2 = 1.6 s. |
|
Esercizio 21 - Per l'osservatore O due eventi, A e B, sono simultanei, e sono separati da xB - xA = 600 km. Qual'è la differenza di tempo tra i due eventi per l'osservatore O', per il quale la separazione spaziale tra A e B è di 1200 km ? Evidentemente l'osservatore O' è in moto rispetto ad O. Calcoliamo dapprima la velocità relativa tra i due. Sostituendo i termini noti in: x'B - x'A = [(xB - xa) - v•(tB - tA)] / [1 - (v/c)2]1/2 si ha: 1.2•106 m = [6•105 m - v•(0)] / [1 - (v/c)2]1/2 che, risolta rispetto a v/c dà: v/c = 0.866. Dopo di che, sostituendo tutti i termini noti in t'B - t'A = [(tB - tA) - (v/c2)•(xB - xA)] / [1 - (v/c)2]1/2, si ha: t'B - t'A = [0 - (0.866/(3•108 m/s)]•3•105 m / [1 - 0.8662]1/2 = - 3.46•10-3 s. Il segno meno del risultato indica che per O' l'evento B precede l'evento A. |
|
Esercizio 22 - L’osservatore O’ parte da una piattaforma spaziale e viaggia alla velocità v = 0.8•c verso Alfa Centauri, che dista dalla piattaforma 4 anni luce. Quando raggiunge la stella, inverte subito la rotta e ritorna alla piattaforma, sempre alla stessa velocità. Quando O’ ritorna alla piattaforma, confronta la sua età con quella del fratello gemello O, che è sempre rimasto sulla piattaforma. Secondo O, il tempo impiegato da O’ per viaggiare dalla piattaforma ad Alfa Centauri è dato da: Dt = distanza / velocità = 4/0.8 = 5 anni. Allora, sempre secondo O, il tempo di andata e ritorno è di 10 anni. Per O’, invece, il tempo di viaggio dalla piattaforma alla stella è un tempo proprio Dt0, ed è dato da : Dt0 = Dt•[1 - (v/c)2]1/2 = 5 anni•[1 - 0.82]1/2 = 3 anni. Allora, secondo O’, il tempo del viaggio di andata e ritorno è di 6 anni. Quindi, quando i due gemelli si incontrano, O’ è più giovane di O di 4 anni. La velocità lo ha ringiovanito di quattro anni. Si osservi che il moto dei gemelli è chiaramente non simmetrico. Per ritornare a casa, il gemello che viaggia deve invertire la rotta. Questa inversione di rotta è reale (O’ subisce delle accelerazioni misurabili) in contrapposizione con l’inversione di rotta apparente che O’ osserva nei riguardi di O (che non subisce alcuna accelerazione durante l’intera vicenda). Perciò il moto di O’ è equivalente a quello di due diversi osservatori inerziali, l’uno che si muove con velocità v = + 0.8•c, e l’altro che si muove con velocità v = -0.8•c. Il gemello O, d’altra parte, è equivalente a un unico osservatore inerziale. |
|
LA GRAVITA' NELL'AMBITO DELLA RELATIVITA' Si considerino questi tre punti:
Subito dopo la formulazione della teoria della r.r., Einstein si dedicò al problema di introdurre la gravità nell’ambito della r.r. All’inizio incontrò notevoli difficoltà. Un'altra questione preoccupava Einstein: siccome il primo assioma della r.r. faceva riferimento a sistemi di riferimento inerziali, egli si chiese perché solo quei sistemi godevano di quel privilegio. Si chiese se si poteva fare in modo che anche sistemi di riferimento accelerati potevano essere accettati dalla r.r. |
|
MASSA GRAVITAZIONALE E MASSA INERZIALE Richiamiamo brevemente le definizioni delle due. Massa gravitazionale di un corpo è la quantità di materia contenuta nel corpo, definita tramite la forza gravitazionale che esso è capace di esercitare. La massa inerziale, invece, è la quantità di materia del corpo, definita attraverso la forza necessaria per conferirgli una certa accelerazione. Le due sono esattamente equivalenti (ma non esiste una teoria universalmente accettata del perchè debba essere così). |
|
PROPORZIONALIA' DIRETTA TRA MASSA INERZIALE E MASSA GRAVITAZIONALE Nella meccanica classica a proposito di massa inerziale e di massa gravitazionale si studia quanto segue:
Si considerino queste due ben note formule della fisica classica: F = G • Mg • mg / r2 (1) e F = mi • a (2) In esse si ha: F forza di interazione gravitazionale tra pianeta e punto materiale. Mg, mg masse gravitazionali del pianeta e del punto materiale. G costante della gravitazione universale (6.67•10-11 N•m2/Kg2). mi massa inerziale di un corpo. a accelerazione conseguente a forza F applicata a massa mi. Eguagliando i secondi membri delle (1) e (2) si ha: G•Mg•mg/r2 = mi•a, da cui a = G•Mg•mg/(r2)•mi Siccome sulla base di accurate misure è stato stabilito definitivamente che mg/mi = 1, si ha in definitiva: a = G•Mg/r2 Il significato dell'ultima espressione è chiaramente che per una data r (altezza dal suolo), l'accelerazione di gravità è una costante per qualunque corpo materiale. |
|
ALCUNI ESPERIMENTI IDEALI Siamo in un ascensore che precipita in caduta libera. Il pavimento sfugge via dai nostri piedi con la stessa velocità del nostro corpo. Quindi i nostri piedi non poggiano sul pavimento. Se abbandoniamo la cartella che tenevamo in mano, essa rimane ferma alla stessa altezza. Apparentemente si tratta della stessa situazione sperimentata da astronauti su una navicella su un'orbita molto lontana dalla Terra. Pur trattandosi di una situazione fisica diversa, vengono osservati gli stessi fenomeni. Concludiamo dicendo che, se ci troviamo in un ambiente molto piccolo, chiuso, nessun esperimento, all’interno, può rivelarci se ci troviamo in un ascensore in caduta libera o in una navicella a grande distanza dalla Terra. Ora vediamo una situazione speculare rispetto a quella sopra descritta. Siamo su un'astronave a grandissima distanza da Terra che accelera (tramite razzi di poppa). L'accelerazione fa sì che i nostri piedi poggino regolarmente sul fondo dell'astronave. Anche qui, se l'ambiente in cui ci troviamo è chiuso e molto piccolo, nessun esperimento condotto all'interno può rivelarci se siamo su un'astronave che accelera a grande distanza dalla Terra oppure su un'astronave ferma sulla rampa di lancio in attesa di partire. Questi ragionamenti portarono Einstein a formulare il principio di equivalenza. |
|
PRINCIPIO DI EQUIVALENZA DI EINSTEIN Stabilisce che in una regione limitata di spazio-tempo è possibile scegliere opportunamente un sistema di riferimento in modo da simulare l'esistenza di un campo gravitazionale uniforme, o viceversa, in modo da eliminare effetti della forza di gravità. |
|
PRINCIPIO DI RELATIVITA’ GENERALE Il principio di equivalenza permise a Einstein di estendere la relatività ristretta per la quale tutte le leggi fisiche assumono la stessa forma soltanto con sistemi riferimento inerziali. Einstein giunse alla conclusione che non c’era motivo di ritenere i sistemi di riferimento inerziali privilegiati. Ciò che accade nei sistemi inerziali, in cui non agiscono forze producenti accelerazioni, avviene indistinguibilmente anche nei sistemi in caduta libera, all’interno di un campo gravitazionale. Allo stesso modo, ciò che avviene in un sistema inerziale sottoposto alla gravità, è identico a ciò che accade in un sistema accelerato. Einstein compendiò quanto sopra enunciando il principio di relatività generale secondo cui le leggi della fisica hanno la stessa forma in tutti i sistemi. Esempio: su un’astronave con moto rettilineo uniforme (sistema di riferimento inerziale) la traiettoria della luce proveniente da una stella "appare" rettilinea a un passeggero. Se l'astronave accelera (diventando un riferimento non inerziale), la traiettoria della luce si comporrà con il moto accelerato e quindi "apparirà" al passeggero curva. |
|
GRAVITA’ E CURVATURA DELLO SPAZIO-TEMPO Nel 1916 Einstein espose la teoria organicamente completa della relatività generale. Essa si basa su alcuni punti fondamentali:
|
|
SPAZI PIATTI E SPAZI CURVI Per millenni l’unico spazio preso in considerazione dai matematici è stato quello euclideo tridimensionale. Euclideo perché in esso è valido il postulato della parallela (per un punto dato passa una sola parallela a una retta data). E’ anche quello in cui, congiungendo tre suoi punti qualsiasi, si ottiene un triangolo nel quale la somma dei tre angoli interni è esattamente un angolo piatto. Nei primi decenni del secolo XX, alcuni matematici, modificando il postulato della parallela di Euclide pervennero a definire tipi di spazio diversi da quello euclideo. Nella teoria geometrica generale di Riemann, per ogni spazio si può definire una sua proprietà intrinseca speciale, detta curvatura. Secondo la teoria, spazi a geometria ellittica hanno curvatura positiva (in essi la somma degli angoli di un triangolo qualsiasi è maggiore di angolo piatto). Spazi a geometria iperbolica hanno curvatura negativa (somma degli angoli di un triangolo qualsiasi, minore di un angolo piatto). Questi due tipi di spazi sono detti curvi. Spazi come quello tridimensionale euclideo, o quello quadridimensionale di Minkovsky hanno curvatura nulla e sono detti piatti (somma degli angoli di un triangolo qualsiasi è esattamente un angolo piatto). |
|
EQUAZIONI DEL CAMPO DI EINSTEIN Nella relatività ristretta lo spazio-tempo è piatto. Nella relatività generale esso dipende dalla distribuzione delle masse. Nota la distribuzione delle masse, l’equazione del campo di Einstein permette di calcolare la geometria dello spazio-tempo risultante. |
|
CURVE GEODETICHE Sono così dette quelle curve che, per ogni tipo di spazio, uniscono due suoi punti con percorso minimo tra di essi. Nello spazio euclideo, a due o tre dimensioni, le geodetiche sono rette. Su una superficie sferica (che è bidimensionale) le geodetiche sono cerchi massimi. Consideriamo due punti materiali situati sull’equatore terrestre e separati da una certa distanza. Supponiamo che i due punti procedano rigorosamente entrambi verso nord (ammettiamo idealmente che etrambi siano dotati di un pilota automatico perfetto). Un osservatore esterno, notando il loro progressivo avvicinamento, potrebbe essere indotto a ritenere che tra i due punti si eserciti una forza attrattiva. Invece sappiamo che l'avvicinamento è dovuto alla curvatura della superficie su cui i due punti si muovono: essi si muovono secondo le geodetiche dello spazio al quale appartengono. Per avere un’idea della curvatura dello spazio-tempo pensiamo a due palle massive posate su un telo teso. Le due masse deformano il telo in tutti i punti di contatto e la deformazione si trasmette ad altri punti del telo. La deformazione del telo si ritorce sulle due palle obbligandole a muoversi fino a raggiungere una posizione di riposo. Il movimento delle due palle per raggiungere la posizione di riposo avviene secondo le geodetiche proprie di quello spazio deformato. |
|
RELATIVITA' RISTRETTA E GENERALE Come per la relatività ristretta gli effetti si rendono evidenti quando ci si avvicina alla velocità della luce, per la relatività generale, gli effetti diventano sensibili quando si ha a che fare (1) con grandi masse e (2) con grandi densità di materia. Partendo dalle equazioni del campo di Einstein, è possibile dimostrare che in un universo quasi piatto, quale quello in vicinanza Terra, la curvatura dello spazio-tempo produce effetti praticamente indistinguibili da quelli risultanti dalle leggi newtoniane. Quindi la teoria di Einstein completa la newtoniana e la contiene come caso particolare. Per la maggior parte dei fenomeni terrestri è sufficiente applicare le leggi newtoniane. |
|
SPAZIO-TEMPO CURVO E LUCE Abbiamo visto che in sistema di riferimento accelerato la luce segue una traiettoria curvilinea. Siccome per il principio equivalenza, gli effetti che si hanno in un sistema accelerato sono simili a quelli che si hanno in un campo gravitazionale, ci chiediamo se la curvatura dello spazio-tempo possa deviare la luce. C’è un'altra ragione per porsi questo quesito. La luce trasporta energia e abbiamo visto che l'energia è interscambiabile con la massa. |
|
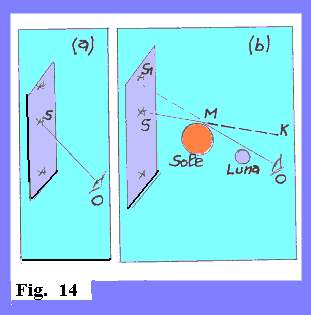
VERIFICA SPERIMENTALE DELLA DEVIAZIONE DI UN RAGGIO DI LUCE Eseguendo nell'ambito della teoria della relatività generale il calcolo della deviazione subita da un raggio di luce transitante in vicinanza del Sole si ottiene il risultato di circa 1.75 secondi di arco. Nella parte (a) della figura , l'osservatore O osserva la stella S, secondo la direzione OS. Nella parte (b) la stessa stella, avente direzione originale SK, viene osservata durante una eclisse totale di Sole, ma perviene all'osservatore O secondo la visuale MO, perché il raggio originale SM subisce la deviazione angolare SMO. L'angolo S1MS, fu misurato durante una eclisse totale nel 1919 e durante altre eclissi successive, e fu trovato effettivamente di circa 1.75 secondi arco, in accordo con il calcolo previsto secondo la teoria della relatività generale. |
 |
|
REDSHIFT GRAVITAZIONALE La teoria della relatività generale prevede un redshift gravitazionale, cioè uno spostamento verso il rosso della frequenza della luce che parte da una stella e arriva a noi. Abbiamo visto che (1) la luce trasporta energia, che (2) la massa è interscambiabile con l’energia e (3) che il campo gravitazionale agisce sulle masse. Viene spontaneo chiedersi se esso possa agire anche sulla luce. La risposta è affermativa: la luce che parte da una stella e che “sale gravitazionalmente” fino a noi, subisce l'influenza della gravità per cui la frequenza di arrivo è minore (spostata verso il rosso) di quella di partenza. |
|
ONDE GRAVITAZIONALI Essendo la geometria spazio-tempo di una regione funzione della distribuzione delle masse, una variazione brusca della loro distribuzione deve causare una perturbazione nella geometria dello s-t, perturbazione che si deve trasmettere a velocità c. Si dovrebbe avere un ‘ onda gravitazionale di perturbazione. Questa brusca perturbazione della geometria dello s-t potrebbe, ad esempio, porre in oscillazione una massa, oppure potrebbe far variare la distanza tra due masse. Occorre tenere presente che le onde gravitazionali interagiscono molto debolmente con la materia. Ad esempio, una che attraversi il Sole perderebbe soltanto una parte su 1016 della sua energia. Onde gravitazionali di intensità relativamente elevata potrebbero essere causate dall' esplosione di supernovae. La probabilità che un tale evento si abbia nelle nostre regioni dell'universo è molto bassa. Finora nessun esperimento è stato in grado di rilevare onde gravitazionali. Per ora sono stati notati soltanto effetti indiretti di onde gravitazionali ad esempio, perdita di energia da un sistema binario di stelle che, ruotando rapidamente, irraggia onde gravitazionali. |