Astronomia islamica medioevale

L'ESPANSIONE ISLAMICA
Il 16 luglio dell'anno 622 d.C. il profeta Muhammad (Maometto) fu costretto a fuggire dalla città della Mecca verso Medina, dall'ostilità delle autorità politiche e religiose che si vedevano minacciate dalla sua predicazione, consistente essenzialmente nel rifiuto dei culti politeistici e nell'esortazione alla venerazione di un unico Dio. Nel giro di pochi anni Maometto rientrò in trionfo alla Mecca (630), due anni prima della sua morte. Il Calendario islamico (lunisolare) venne canonizzato nel 638 dal secondo califfo Omar. L'anno 1 del Calendario islamico venne posto al 622 d.C.

Dodici anni dopo la morte di Maometto, conclusa l'adesione all'Islam (Islam = "sottomissione incondizionata") in tutta la penisola arabica, incominciò l'espansione all'infuori di essa. Nel 709 l'intero Nordafrica era conquistato. Dal 712 l'espansione si estese alla Spagna e si arrestò soltanto nel 732 con la sconfitta di Poitiers inflitta agli Islamici dai Franchi di Carlo Martello. Verso est l'espansione si produsse con la conquista della Persia e della Transoxiana.

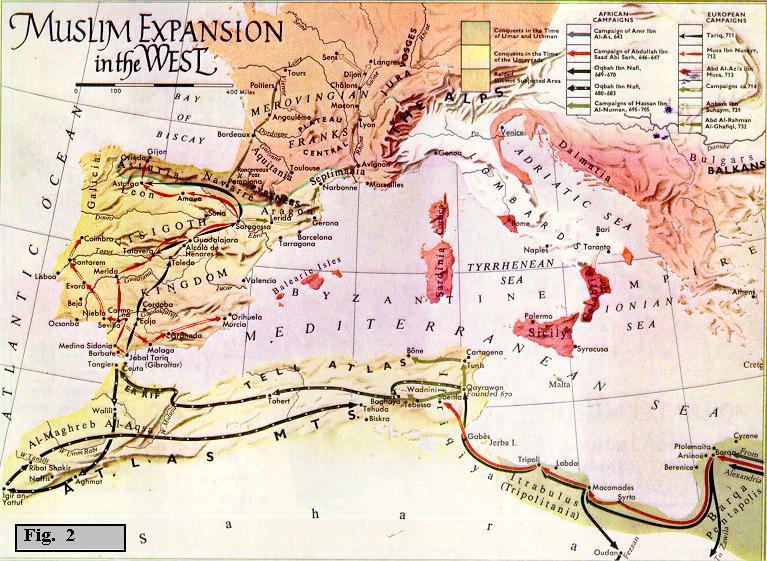
La leadership dell'Islam è strettamente associata all'affermazione di due dinastie, quella degli Omayyadi e quella degli Abbassidi. Fondatore della prima dinastia fu il califfo Muawiya I, il cui padre, un tempo avversario di Maometto, era già riuscito a imporsi ai suoi tempi. Stabilita la sede del califfato a Damasco, questa dinastia raggiunse l'apice della sua potenza con il califfo al-Walid (705 - 717) che, pur non riuscendo a invadere l'Impero bizantino, estese il dominio dell'Islam dai confini della Cina alla Spagna meridionale.

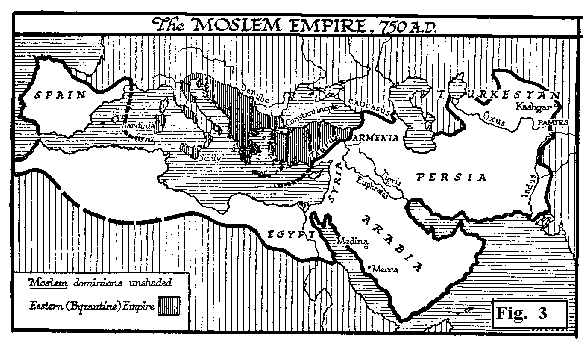
La religione e la cultura islamica si svilupparono nei due filoni dottrinali principali sunnita e sciita.
Occorre dire che la religione islamica non venne imposta con la forza ai popoli conquistati (per lo meno nella fase successiva), non solo perchè era ritenuta esclusiva degli Arabi, ma perchè il loro sistema fiscale era basato su tasse che gravavano esclusivamente su sudditi non musulmani.

Una rivolta guidata dalla famiglia degli Abassidi mise fine nel 750 al califfato omayyade. L'unico componente della dinastia omayyade che riuscì a scampare al massacro fu Abd ar-Rahman I che si rifugiò in Spagna dove occupò Cordova e Siviglia, dando vita all'Emirato autonomo di Andalusia.

Eponimo della dinastia Abasside fu al-Abbas, zio di Maometto. Scacciati gli Omayyadi, gli Abbassidi trasferirono la capitale da Damasco a Baghdad, fondata nel 762 dal califfo al-Mansur (754 - 775).
I califfi abassidi riuscirono a mantenere sia il potere politico che l'autorità religiosa per oltre un secolo. Il massimo splendore della dinastia fu raggiunto con Harum ar-Rashid. Alla sua morte, i due figli si contesero il trono e prevalse al-Mamun. Da allora le lotte intestine minarono il prestigio della famiglia che attraversò una continua fase di debolezza che culminò alla metà del XIII secolo quando i Mongoli si impossessarono di Bagdad uccidendo l'ultimo califfo abasside.

Oggi nel filone dottrinale Sunnita è compresa la maggioranza (circa l'83%) dei seguaci dell'Islam. Il nome deriva dal concetto di Sunna, la tradizione più antica di norme etiche e morali, stabilite sulla base dei detti e degli scritti di Maometto, noti con il termine di Hadith, e considerati, insieme con il Corano, le fonti principali del diritto islamico. Nel secolo XIII furono accettate come autentiche 14 collezioni di hadith.

L'altra corrente dell'Islam, quella degli Sciiti, si distingue per le origini e le concezioni teologiche. Originariamente il termine "sciiti" (da shiah = seguace) stava ad indicare i sostenitori del partito di Alì, genero di Maometto (avendone sposato la figlia Fatima) e quarto califfo dell'Islam, che essi consideravano unico successore legittimo del Profeta alla guida dell'Islam, e quindi usurpatori i tre califfi precedenti. Alì venne assassinato nel 661 (ancora oggi nella mistica sciita questo fatto è considerato il martirio per eccellenza, che consacra le loro rivendicazioni).

A questa prima fase di lotte a sfondo politico seguirono in epoca omayyade (661 - 750) le tappe dell'elaborazione della teologia caratteristica della comunità sciita. Custodi di questa sapienza (trasmessa ad Alì direttamente da Maometto) sarebbero i legittimi discendenti di Alì, che sono venerati come iman, cioè "guide", della comunità, dotati di poteri sovrannaturali, come l'infallibilità e la capacità di compiere miracoli. Questa visione dottrinale si discosta nettamente da quelle dei sunniti che riconoscono soltanto in Maometto l'ultimo profeta, e che non ammettono poteri soprannaturali degli iman.

Il mondo arabo non tardò a liberarsi del fanatismo che inizialmente sostenne le conquiste militari (si ricordi l'incendio della Biblioteca di Alessandria ordinato nel 641 dal califfo Omar in base al semplice sillogismo di ritenere i libri in essa contenuti inutili se conformi alla fede islamica e dannosi se contrari). Evidentemente quindi la prima fase di espansione dell'Islam fu caratterizzata dalle conquiste militari e dall'ardore della predicazione religiosa. Ma, a partire dal nono secolo, venendo a contatto con la cultura dei paesi conquistati, nel mondo islamico si manifestò un vivissimo interesse per lo studio delle discipline filosofiche, mediche e matematiche. In particolare gli Arabi assimilarono la scienza e la filosofia del Vicino Oriente ellenistico, attraverso le opere di Aristotele, Platone, Euclide, Galeno, che venivano a mano a mano tradotte in arabo.
Anche la conquista della Persia e dell'India si rivelò grandemente benefica per la cultura araba, per i tesori culturali che gli Arabi seppero trarre da quelle preziose civilizzazioni.
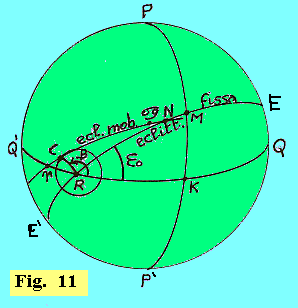
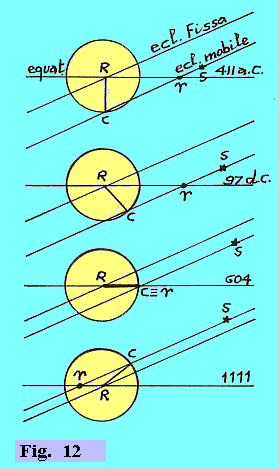
Fra le scienze, particolarmente fecondo fu il travaso di conoscenze astronomiche che gli Arabi acquisirono dai Greci.

Occorre tenere presente che gli astronomi arabi vennero a contatto con l'astronomia greca attraverso due vie. Già fin dai tempi della dinastia Achemenide (V secolo a.C.), che aveva esteso la sua sovranità anche all'India di nord ovest, alcune tecniche astronomiche babilonesi erano filtrate in India. Durante il periodo Seleucide (IV e III secolo a.C.), altre idee astronomiche, questa volta greche (pur miste ad altre tecniche babilonesi) erano nuovamente filtrate in India. Il risultato di queste trasmissioni culturali, avidamente accolte dagli Indiani, fu che si ebbero testi astronomici indiani (scoperti oggi) recanti le teorie degli epicicli prima dell'epoca di Tolomeo. Poichè l'espansione islamica dei secoli VI e VII si estese anche verso l'India, questa acquisizione di idee astronomiche di origine greca fu la prima via di contatto che gli Arabi ebbero con l'astronomia ellenica. La seconda via fu quella più diretta della traduzione delle opere greche, a partire dalla conquista del Nordafrica, specificamente con la caduta di Alessandria.

RELIGIONE ISLAMICA E ASTRONOMIA
Alcuni collocano la nascita dell'astronomia araba all'epoca in cui alcuni saggi indiani recatisi in visita presso la corte di Al Mansour, califfo di Bagdad nel 744, portarono con loro un trattato di astronomia pratica, che subito fu tradotto in arabo con il titolo di “Tavole astronomiche indiane” (“Zig al Sindhind”, letteralmente canoni indiani) da Ibn Ibrahim al Fazari e da Ya'qub Ibn al Tariq.
La religione islamica poneva all'astronomia un certo numero di problemi. C'era anzitutto la necessità di disporre di un efficiente calendario per osservare le ricorrenze religiose alla data corretta. La seconda indicazione astronomica era quella di fornire al credente una regola semplice ed affidabile, la qibla, per consentirgli di rivolgersi verso la Mecca al momento della preghiera. Un'altra indicazione astronomica era quella di fornire al muezzin il modo per chiamare i fedeli alla preghiera nelle ore prescritte (su certi astrolabi arabi si avevano curve per le ore delle preghiere). Ma non si deve pensare che a motivare lo studio dell'astronomia presso gli Arabi siano state unicamente queste ragioni di carattere pratico. Gli Arabi dimostrarono di possedere un genuino amore per la cultura, esaltandola come un dono prezioso proveniente da Dio. Non poterono quindi non aderire pienamente all'ideale ellenistico di amore per la cultura.

L'INCONTRO CON L'ALMAGESTO
Il tipico manuale astronomico arabo era lo Zij. Il prototipo più antico di Zij era una raccolta delle Tabelle dell'Almagesto, accompagnate da un insieme di regole. Uno Zij di successo fu quello redatto dal famoso Al Khwarizmi, matematico ed astronomo vissuto a Bagdad agli inizi del IX secolo. Oltre alle Tabelle, incorporava anche materiale indiano e persiano. Venne tradotto anche in latino.
Un altro Zij molto importante fu quello redatto da Albatenio (al-Battani, 858 - 929), per gli elementi di novità che conteneva, notevoli tra questi il nuovo valore di obliquità dell'eclittica di 23º 35' e il nuovo valore della longitudine dell'apogeo solare, entrambi trovati da al Battani stesso. Questa seconda scoperta fu di enorme valore perchè sanciva il fatto che l'apogeo solare era mobile (l'astronomia alessandrina non era riuscita a pervenire a questo risultato). Lo Zij di Albatenio incontrò un favore maggiore del precedente perchè si rifaceva a metodi più propriamente tolemaici. Anche l'opera principale di Albatenio De scientia stellarum (nella dizione latina) ebbe larga fama. Gli Zij che seguirono questo, fino al secolo XV, furono compilati sulla falsariga di questo di Al Battani.

La prima traduzione in arabo dell'Almagesto fu eseguita, all'inizio del secolo IX è attribuita per tradizione ad al Haggiag ibn Yussuf ibn Matar su ordine originale del califfo Harum al Rashid, della dinastia Abasside. Al Haggiag, della specola di Bagdad, aveva tradotto anche i primi sei libri di Euclide. Il figlio e successore di al-Rashid, il califfo al-Mamun (786 - 833), fece eseguire due traduzioni. Una di queste, eseguita negli anni 827/827, da al-Haggiag, esiste tutt'ora. L'altra traduzione araba esistente è quella eseguita intorno all'892 da Ishaq ibn Hunayn, e in seguito revisionata da Thabit ibn Qurra.
Al nome del grande ed illuminato sovrano al-Mamun sono legate due eccezionali imprese astronomiche, eseguite da suoi astronomi per suo espresso ordime: (1) la misurazione estremamente precisa di 23º 33' dell'obliquità dell'eclittica, nell'anno 830, e (2) l'altrettanto celebre misura del grado di meridiano, nell'anno 828: due gruppi di astronomi percorsero, in sensi inversi, un tratto di pianura mesopotamica, misurando l'altezza del polo fino a trovare una variazione di un grado, ottenendo il valore di 111.683,12 metri, valore pochissimo diverso dal reale, che alla latitudine media della Mesopotamia è di 110.938,0 metri. E' possibile che a sovraintendere a entrambe le misurazioni sia stato Alfragano (Ahmad ibn Muhammad ibn Kathir al-Farghani), uno degli astronomi di al-Mamun, autore del trattato Elementi di astronomia, uno dei primi notissimi compendi dell'Almagesto, tradotto in seguito da Gerardo da Cremona.

CRITICHE A TOLOMEO
Un altro genere di trattati astronomici arabi furono i commentari all'Almagesto. Col tempo, questi commentari assunsero anche aspetti critici su alcuni punti dell'opera che riuscivano poco covincenti.
La cosmologia tolemaica conobbe un diverso e contraddittorio grado di interesse presso gli Arabi. Si ha la netta impressione che il libro di Tolomeo Ipotesi planetarie abbia avuto una scarsa circolazione nel mondo arabo (per lo meno in confronto all'Almagesto). E' difficile trovare opere arabe nelle quali vengano commentati adeguatamente i due aspetti fondametali della cosmologia tolemaica, e cioè il sistema delle sfere solide annidate e le distanze planetarie. In genere, o è affrontato un argomento o è affrontato l'altro. Nel trattato di cosmologia tolemaica di Thabit, le distanze tra i pianeti sono modificate rispetto a quelle di Tolomeo.
Thabit al Farghani nel suo Elementi di astronomia sembra avere poca dimestichezza con l 'opera Ipotesi planetarie di Tolomeo. E' a conoscenza della teoria classica delle sfere annidate ma procede per suo conto nel calcolo delle distanze.
Un aspetto qualificante dell'astronomia araba fu (malgrado la linea fondamentalmente tolemaica) la presenza di numerose critiche di certi aspetti dell'Almagesto. La prima critica fu certamente quella di aver violato i canoni aristotelici per aver adottato moti non uniformi, e per aver introdotto l'equante. Una prima critica su questo soggetto venne a Tolomeo da al Tusi (1201 - 1274).
Ibn al Haytham arrivò a scrivere un libro intitolato Dubbi su Tolomeo. La critica di Haytham raggiunse forse il vero punto focale perchè egli mise in luce l'assurdità di descrivere dei moti di corpi celesti, sulla base di semplici costruzioni geometriche che non avevano alcun fondamento con la realtà, se non una apparenza visuale. Mosé Maimonide (1135 - 1204,israelita) nella sua Guida per i perplessi negò qualunque valore alle costruzioni geometriche degli epicicli e degli eccentri.

Questa visione critica di Tolomeo si consolidò in un gruppo di astronomi che si associarono in un osservatorio a Maragha, in Persia. Alla metà del XIII secolo, Ulugh Beg, nipote di Gengis Khan, fondatore della dinastia Ilkhani e conquistatore di Persia e Mesopotamia, si lasciò persuadere dall'astronomo Nasir al Din al Tusi a fondare e sostenere un notevole osservatorio a Maragha. Nel 1272 gli astronomi operanti a Maragha completarono un nuovo Zij, le Tavole Ilkhani.
Infine, una notevole modifica a Tolomeo fu prodotta da Ibn al Shatir di Damasco, vissuto dal 1304 al 1375 circa, che eliminò l'equante, soltituendolo con un ulteriore epiciclo. Malgrado queste innovazioni abbiano goduto di larga fama nella comunità scientifica islamica, per le modalità di computo delle posizioni planetarie si continuò a rifarsi alla classica procedura tolemaica. Vedremo che l'innovazione di al Shatir di eliminare l'equante, sarà ripresa da Copernico, che potrebbe averla appresa, secondo il parere di alcuni, durante i suoi prolungati soggiorni in Italia.

NOMI ARABI DELLE STELLE
Come è noto, molti nomi di stelle sono di derivazione araba. Ne diamo alcuni esempi. Per l'Orsa Maggiore (Grande Carro), abbiamo Dubhe derivato da Thar al Dubb al Akbar ("il dorso dell'orsa"), Merak da al Marakk ("il lombo dell'orsa"), Phedka da al Fahdah ("la coscia"), Alioth da Alyath ("grassa coda"), Alkaid / Benetnash da al Ka'id Banat al Na'ash ("governatore delle figlie della bara"), Mizar da Mizar ("cavallo").
Nella costellazione dell'Orione ricordiamo Betelgeuse da Na'beit al gueze ("spalla del gigante"), Rigel da Rijil al jauzeh ("la gamba sinistra del gigante"). Del Toro ricordiamo Aldebaran da Na'ir al dabaran ("colei che segue le Pleiadi"). Del Perseo Algol da al Ghul ("spirito mutevole" con riferimento evidente alla sua variabilità). Alcune altre stelle i cui nomi sono di derivazione araba sono Achernar da Akher Nahr ("foce del fiume"), Altair da Al tair ("aquila volante"), Vega da Al nasr al waki ("aquila planante").

AL-KHWARIZMI
Abu Jafar Muhammad ibn Musa Al-Khwarizmi (ca. 780 - 850). Harum al-Rashid era califfo della dinastia Abasside di Bagdad al tempo della nascita di al-Khwarizmi. Dopo le conquiste militari (dal Mediterraneo all'India) al-Rashid incominciò a favorire la fioritura culturale nel suo regno. Alla morte di al-Rashid, il conflitto tra i due figli si concluse con la soppressione del maggiore e il trionfo del minore, al-Mamun, nell'813. Questi, seguendo le orme del padre, continuò ad esercitare il suo patronato su arti e scienze, fondando a Bagdad un'accademia di sapienti, chiamata Casa della saggezza, dove ebbe inizio il lavoro di traduzione di opere classiche greche. Fondò anche una libreria dove vennero collezionati manoscritti provenienti da Bisanzio e diversi osservatori astronomici.

Al Khwarizmi iniziò la sua attività astronomica con traduzioni dal greco, ma anche con la scrittura di suoi lavori. Uno dei primi fu il trattato Hisab al-jabr wal muqabala che è considerato la sua opera più importante e il primo libro sull'algebra (la parola "al-Jabr", che si riferisce ad un particolare passaggio nel procedimento risolutivo delle equazioni detto “regola del trasporto”, è la matrice della nostra parola Algebra).

Un altro lavoro matematico di al-Khwarizmi di enorme importanza fu un trattato sulla numerazione indo-araba. Nella traduzione latina, il titolo era Algoritmi de numero Indorum (come dal primo lavoro nacque la parola algebra, da questo, per derivazione dal suo nome, nacque la parola algoritmo). Si tratta chiaramente del sistema di numerazione posizionale decimale usato dagli Indiani, con la probabile introduzione per la prima volta della cifra zero.
Altro importante lavoro di al-Khwarizmi, questa volta in astronomia fu Sindhind zij, un trattato astronomico, basato su testi astronomici indiani che erano stati dati in dono alla corte Abasside da una missione diplomatica indiana, intorno all'anno 770, quindi uno dei primi contatti degli arabi con l'astronomia indiana (calendari, calcolo della posizione del Sole vero, della Luna e dei pianeti, tavole di seni e tangenti, astronomia sferica, tavole astrologiche). Al-Khwarizmi compilò due versioni di questa sua opera, ma entrambe andarono perdute. Nel decimo secolo un astronomo arabo, al-Majriti, eseguì una revisione critica di una delle due versioni e questa venne tradotta da Adelardo di Bath. Dell'altra versione del Sindhind zij di al-Khwarizmi venne pure eseguita in seguito una traduzione in latino.

AL-FARGHANI (ALFRAGANUS)
Abul Abbas Ahmad ibn Muhammad ibn Kathir al-Farghani (ca 800 - 870). Nacque a Farghana, nell'attuale Uzbekistan. Fu uno dei più famosi astronomi al servizio del califfo al-Mamun e dei suoi successori. Scrisse Kitab fi al-Harakat al-Samawiya, "Elementi di astronomia", un trattato elementare di astronomia tolemaica che ottenne molta popolarità per la sua accessibilità.

Il trattato venne tradotto in latino nel secolo XII e godette di popolarità anche in Europa fino al tempo della Sphaera di Sacrobosco, con successive traduzioni. La presenza di innumerevoli manoscritti latini degli "Elementi" di al-Farghani nelle biblioteche europee testimonia la grande popolarità che ebbe la sua opera. Gli specialisti ritengono che fu dagli "Elementi", nella traduzione di Gerardo da Cremona, che Dante trasse le cognizioni astronomiche esposte nel Convivio e nella Vita Nova. La sua cosmologia rivela che egli ebbe una visione abbastanza chiara del principio delle sfere annidate ma nessuna dimestichezza con la cosmologia delle Ipotesi planetarie di Tolomeo. A partire dai parametri dell'Almagesto produsse un calcolo autonomo delle massime e minime distanze di ogni sfera planetaria. Eseguì anche una determinazione abbastanza precisa del diametro della Terra.
Il Fihrist ("Indice") scritto da Ibn al-Nadim nel 987, attribuisce ad al-Farghani un'altra opera di carattere astronomico: Kitab amal al-Rukhamat ("Libro sulla costruzione di orologi solari"). Svolse anche attività ingegneristica al servizio del suo sovrano, specialmente nello scavo di canali.

THABIT IBN QURRA
Al-Sabi Thabit ibn Qurra al-Harrani (ca. 826 - 901). Nacque ad Harran, la località allora mesopotamica di Carre (oggi turca) dove i Romani guidati da Crasso avevano subito la famosa disfatta dai Parti. La sua famiglia apparteneva alla setta religiosa dei Sabiani, nel culto della quale era riconosciuta l'adorazione delle stelle. Il prenome Al-Sabi mantenuto da Thabit, lascia supporre che egli non si sia convertito all'Islam. La setta aveva mantenuto legami con la cultura greca tanto che era rimasta la tradizione, per i membri della setta, di praticare la lingua greca. Thabit, oltre che naturalmente la lingua araba, aveva dimestichezza sia con il greco che con il siriaco.
La famiglia facoltosa lo convinse ad andare a Bagdad per ricevervi una adeguata istruzione matematica e medica. Al suo ritorno ad Harran, a causa delle sue vedute filosofiche troppo liberali acquisite durante gli studi a Bagdad, dovette subire una persecuzione religiosa da parte degli ambienti conservatori della sua setta e decise perciò di emigrare definitivamente a Bagdad. Là si guadagnò la protezione del califfo al-Mutadid, uno dei più celebri della dinastia Abbasside, che lo nominò astronomo di corte.

Ma una attività di enorme importanza alla quale si dedicò Thabit fu quella della traduzione di opere greche, specialmente di carattere matematico. Sappiamo che le prime due traduzioni in arabo degli Elementi di Euclide, andate perdute tranne che per alcuni frammenti, furono eseguite da al Haggiag. Sono sopravvissuti invece numerosi manoscritti, copie di una terza traduzione degli Elementi eseguita da Hunayn ibn Ishak. Thabit aveva sottoposto la traduzione di Hunayn a una revisione critica. Gli specialisti hanno accertato che la gran parte delle successive versioni arabe degli Elementi, si basarono su questa revisione di Thabit.
Ma Thabit non fu soltanto un provetto traduttore di opere greche. Fu un brillante matematico che diede notevoli contributi allo sviluppo di questa scienza.

Thabit scrisse anche opere astronomiche nelle quali si fa un grande uso di matematica. La sua opera più conosciuta è Del moto dell'ottava sfera (andata perduta), nella quale venne sviluppata la teoria della trepidazione (movimento oscillatorio degli equinozi e di tutta l'eclittica, al quale dedicheremo un paragrafo in seguito).
Altri suoi lavori astronomici sono giunti fino a noi e sono considerati fondamentali per aver consolidato matematicamente la giovane scienza astronomica araba del suo tempo. In particolare si occupò in maniera attenta e meticolosa dei moti della Luna e del Sole, ritenendo che l'osservazione delle eclissi di Sole e di Luna fossero l'unico modo per determinare la posizione della Luna con esattezza e che dalla durata del ciclo delle eclissi fosse possibile determinare la periodicità dei moti del Sole e della Luna con una semplice divisione (in ciò riprese analoghi studi di Tolomeo).

AL-BATTANI (ALBATENIUS)
Abu Abdallah Mohammad ibn Jabir Al-Battani (ca. 850 - 929). Anche lui, come Thabit Qurra, nacque ad Harran e anche la sua famiglia apparteneva alla setta dei Sabiani. Ma si ritiene che il nome "Abu Allah Muhammad" indichi che Al-Battani, a differenza di Thabit Qurra, fosse di fede islamica. Dunque, di una generazione più giovane di Thabit, non si può escludere che i due si siano frequentati.
Incominciò la sua carriera di osservatore astronomico (e di fabbricante di strumenti astronomici) nelle località siriane di Ar-Raqqah e di Antiochia. Esiste una documentazione (Fihrist, "Indice"), del secolo X attestante il livello elevato della fama di cui era gratificato al suo tempo sia per la qualità delle sue osservazioni astronomiche che per le sue opere.
Secondo questo Fihrist egli osservò tra gli anni 877 e 918, mentre il suo catalogo stellare è dell'anno 880. I suoi lavori elencati nel Fihrist sono Kitab al-Zij e un commentario al Tetrabiblos di Tolomeo.

Il Kitab al-Zij è la sua più importante opera. Comprende 57 capitoli nei quali gli argomenti si succedono secondo lo schema classico degli Zij: introduzione di strumenti matematici, teoria astronomica, tavole.
Vediamo in breve quali furono i più importanti risultati conseguiti da Al-Battani. Diede un catalogo di 489 stelle. Perfezionò l'accertamento della durata dell'anno a 365 giorni, 5 ore, 48 minuti, 24 secondi. Diede per la precessione degli equinozi il valore annuale di 54".5 e di 23º 35' per l'obliquità dell'eclittica. Accertò la progressione della longitudine dell'apogeo solare e la possibilità di avere anche eclissi di Sole anulari. Secondo alcuni, però, l'autorità di Tolomeo al tempo di Al-Battani era tanto grande che, malgrado i suoi calcoli gli avessero fatto determinare che la distanza del Sole si scostava notevolmente da quella stabilita da Tolomeo, non osò affermarlo pubblicamente. Dove invece manifestò con chiarezza la propria contestazione a Tolomeo fu nel metodo tolemaico di determinazione del diametro apparente della Luna: al-Battani afferma infatti che la Luna può assumere un diametro apparente minore di quello del Sole e ciò spiega perché si verificano le eclissi anulari. Afferma poi che lo stesso diametro solare può variare, contrariamente a quanto sosteneva Tolomeo.
I commentatori sono concordi nell'affermare che l'importanza di Al-Battani nello sviluppo della scienza si manifestò specialmente nell'influenza che le sue opere ebbero su scienziati quali Copernico, Brahe e Galileo.
Il Kitab al-Zij di Al-Battani venne tradotto in latino nel 1116 da Platone da Tivoli con il titolo De motu stellarum. Un'altra traduzione venne eseguita nel XIII secolo in Spagna, ed entrambe fortunatamente ci sono pervenute.

IBN YUNUS
Abul Hasan Ali Abd al-Rahman ibn Yunus (ca. 950 - 1009).
Nacque in Egitto, probabilmente al Cairo, da una famiglia che aveva dato illustri studiosi. In Egitto regnava la dinastia Fatimide che aveva tratto il nome per discendenza da Fatima, la figlia di Maometto. Questa dinastia era riuscita a imporsi sulla Abbasside, conquistando nella prima metà del secolo X il Nordafrica e la Sicilia.
Ibn Yunus divenne un protetto del califfo Al-Aziz che, malgrado fosse sempre impegnato in operazioni militari fino all'ultimo giorno della sua vita, lo favorì nel consentirgli di iniziare la sua attività astronomica. Dopo la morte di Al-Aziz il califfato passò al figlio al-Hakim e si ritiene che anche lui abbia continuato a proteggere l'attività astronomica di Ibn Yunus, sebbene sembra che il nuovo sovrano fosse più interessato ai responsi astrologici del suo protetto.
Il suo lavoro più importante fu uno Zij: al-Zij al-Hakimi al-kabir, dedicato, come dice il titolo, al sovrano. Di 81 capitoli, conteneva osservazioni eseguite da Yunus e da suoi predecessori, una caratteristica questa piuttosto singolare (gli altri autori, in genere, non facevano distinzione tra le proprie osservazioni e quelle di altri).
La gran parte del materiale di quest'opera di Yunus era costituita da tavole di vario tipo alle quali fecero ricorso anche altri autori di epoche successive.
I suoi biografi sono concordi nell'affermare che predisse la data della sua morte con sette giorni di anticipo, che si ritirò in casa ad attenderla serenamente recitando versetti del Corano.

AL-HAITHAN (ALHAZEN)
Abu Ali Hasan Ibn al-Haithan (Alhazen) (ca. 965 - 1040). Nacque a Bassora, nell'attuale Irak meridionale. Ricevette la sua educazione a Bagdad. E' considerato il padre dell'ottica moderna. Trascorse la maggior parte della sua vita in Spagna, dove condusse ricerche di ottica, matematica e fisica.
Studiò la rifrazione della luce attraverso l'aria e l'acqua, giungendo a scoprire le leggi della rifrazione. Arrivò molto vicino a scoprire le leggi delle lenti di ingrandimento.
Il suo libro Kitab-al-Manazir tradotto in latino con "Opticae thesaurus" servì da base per le ricerche sull'ottica di Roger Bacon, Pole Witelo, Leonardo da Vinci e Keplero.
Contraddisse la credenza che risaliva a Euclide e Tolomeo, secondo i quali la visione era dovuta a raggi emessi dall'occhio, affermando invece che i raggi visivi provenivano dagli oggetti. Contraddisse anche la introduzione dell'equante da parte di Tolomeo, però unicamente sulla base della violazione dei principi della fisica aristotelica. A lui sono attribuiti i primi esperimenti sull'uso della camera oscura. Scrisse più di duecento libri dei quali solo pochissimi sono sopravvissuti.

AL-BIRUNI
Abu Arrayhan Muhammad ibn Ahmad al-Biruni (973 - 1048). Nacque nell'attuale Karakalpakstan (Uzbekistan) a Kwarizm, sul Lago d'Aral. Il suo luogo natale oggi è chiamato Biruni, in suo onore. Iniziò i suoi studi sotto la guida del famoso astronomo e matematico Abu Nasr Mansur. Nel 990, giovanissimo eseguì la misurazione della latitudine del suo luogo natale. All'età di 22 anni aveva già portato a termine una serie di brevi scritti scientifici, uno dei quali Cartografia, un trattato sulle proiezioni che è sopravvissuto e che, oltre a sue idee originali, mostra una vasta cultura sull'argomento per le estese citazioni su altre opere.

Nel 995 la famiglia regnante, Banu Iraq, venne rovesciata da un colpo di stato ed al-Biruni dovette mettersi in salvo. Non è chiaro sapere cosa accadde in questo frangente al suo maestro Abu Nasr Mansur, che era un principe di quella famiglia. Si sa che nella città di Ravy, presso l'attuale Teheran, riuscì a svolgere attività astronomica negli anni dal 995 al 997, ma sempre sotto l'assillo di ristrettezze economiche. In questo periodo ebbe modo anche di collaborare con il famoso Abul Wafa. Essi decisero di osservare una eclisse di Luna, (24 maggio 997), al Biruni a Kath, e Abul Wafa a Bagdad, in modo da ricavare la differenza di longitudine tra le due località.
Si sa che intorno all'anno 1000 dedicò il suo libro Cronologia a Qabus, regnante sullo stato di Ziyarid, dal che dobbiamo arguire che gli aveva accordato la sua protezione. In questo libro al-Biruni cita anche sette sue opere precedenti, una delle quali soltanto di argomento storico e le rimanenti tutte di argomento astronomico.
Sappiamo che il 4 giugno 1004 egli era di ritorno al suo luogo natale perchè quel giorno osservò un eclisse di Luna.
Nel 1004, regnando su quel territorio Abul Abbas Mamun, al-Biruni potè fruire del suo generoso supporto, che, forse per intercessione di al-Biruni stesso, il signore estese anche al vecchiuo maestro di al-Biruni, il principe Abu Nasr Mansur, per cui i due scienziati ebbero la ventura di tornare a lavorare assieme. Ma la guerra doveva nuovamente interrompere gli studi di al-Biruni. Nel 1017 la regione venne occupata militarmente e passò sotto il controllo del sovrano di Ghazna al-Mahmud e i due scienziati, virtualmente prigionieri del nuovo sovrano, dovettero seguirlo a Ghazna.
Il periodo che segue è piuttosto di difficile interpretazione perchè sembra che, malgrado al-Biruni abbia potuto svolgere una certa attività scientifica, abbia dovuto subire al contempo anche delle privazioni.
La complessità della relazione tra al-Biruni e il suo signore Mahmud è deducibile anche dal fatto che al-Biruni dovette seguirlo durante una campagna militare che il sovrano condusse in India, durante la quale al-Biruni ebbe modo di eseguire determinazioni di latitudini di diverse località del Punjab fino ai confini del Kashmir. Di questa esperienza indiana al-Biruni lasciò una descrizione in una sua opera famosa, India, che ci è pervenuta. Si tratta di un'opera di enorme importanza per la gran quantità di notizie su diversi aspetti di quel paese: la religione, le tendenze filosofiche, il sistema di caste e le usanze matrimoniali. Al-Biruni studia poi il sistema di scrittura e quello di numerazione. Infine viene studiata l'astronomia , l'astrologia e il calendario indiani.
Al-Biruni studiava la letteratura indiana dall'originale sanscrito del quale era un esperto traduttore in arabo. Affrontava in questa lingua gli argomenti più disparati, quali astronomia, astrologia, cronologia, geografia, grammatica, matematica, medicina, filosofia, religione, sistemi di pesi e misure.
Il sovrano Mahmud morì nel 1030 e il potere passò al figlio anziano Masud, che sembra aver trattato Al-Biruni meglio di quanto aveva fatto il padre, perchè godette di una sostanziale libertà di movimento.
Masud venne assassinato nel 1040 e a lui successe il figlio Mawdud. La produzione di scritti da parte di Al-Biruni fu impressionante. E' stato calcolato che egli abbia prodotto non meno di 146 trattati, per un totale di circa 13.000 pagine.
E' stato messo in evidenza dai commentatori l'approccio rigorosamente scientifico che Al-Biruni ebbe nel trattare i suoi argomenti. Per esempio nella trattazione dei dati, contrariamente a Tolomeo che aveva l'abitudine di selezionare i dati spesso quando si accordavano con le sue teorie. Al-Biruni invece, quando decideva di scegliere un dato, citava anche quelli che non si accordavano con quello scelto. Poneva una particolare cura negli arrotondamenti e anche nell'osservare grandezze che richiedevano il minimo di manipolazioni.
Uno dei più importanti testi di Al-Biruni ha per titolo Ombre, che si ritiene sia stato scritto intorno al 1021. Costituisce una importante sorgente per la conoscenza della storia della matematica e della fisica. Contiene una gran quantità di nozioni su fenomeni riguardanti l'utilizzazione delle ombre per la soluzione di problemi scientifici. Contiene anche importanti idee sui moti accelerati e quelli uniformi, sull'uso di un sistema di riferimento a tre coordinate.
A lui viene attribuito il primo uso delle funzioni trigonometriche (il seno si ritiene derivi dalla latinizzazione “sinus” di una parola araba che significa semicorda). Una argomentazione in cui manifestò una certa indipendenza da Tolomeo fu nel ritenere possibile, in linea teorica, la rotazione della Terra (Tolomeo affermava che se la Terra ruotasse i corpi non cadrebbero verticalmente ma verrebbero trascinati dalla rotazione. Per al-Biruni, invece, ogni corpo è trascinato dalla rotazione della Terra lungo la verticale di caduta.

Un aspetto importante dell'attività scientifica di Al-Biruni è dato dalla corrispondenza che intrattenne con altri scienziati. Ebbe un lungo e costante rapporto di collaborazione con il suo maestro Abu Nasr Mansur: ciascuno dei due chiedeva all'altro di affrontare specifici aspetti di un proprio lavoro. Corrispose con il grande Avicenna contrapponendosi a lui su argomenti quali la natura della luce e del calore, ma anche su argomenti astronomici e filosofici. Ebbe corrispondenza anche con al-Sijzi.
Circa la personalità di questo grande scienziato, vale la pena di ricordare che in lui splendette uno dei tratti che suscitano la nostra ammirazione per l'attitudine di tolleranza di cui gli Arabi seppero dar prova in tante circostanze. Al-Biruni non mancò di esprimere il suo dolore nell'apprendere che conquistatori arabi di Khwarazm avevano distrutto testi antichi di altra religione.

IBN SINA (AVICENNA)
Abu Ali al-Husain ibn Abdallah ibn Sina (980 - 1037). Nacque presso Bukhara, nell'attuale Uzbekistan e morì ad Hamadan in Persia. E' largamente conosciuto con l'appellativo occidentale Avicenna, anche se oggi si tende a tornare alla versione originale del nome, Ibn Sina. Si conosce molto della sua vita perchè egli stesso scrisse un'autobiografia ed uno dei suoi studenti scrisse una sua biografia.
Dopo la conquista araba della Persia, la prima dinastia araba a imporsi fu quella Samanide, a partire dal 900. Quando Avicenna nacque il sultano samanide era Nuh ibn Mansur e il suo potere era in declino. Il padre di Avicenna era governatore di un villaggio. La sua casa era un luogo di ritrovo per persone colte che manifestarono presto il loro stupore per la precocità del giovane Ibn Sina.
All'età di tredici anni incominciò a studiare medicina e a sedici anni incominciava a trattare pazienti. La sua fama medica crebbe al punto che il sovrano samanide Nuh ibn Mansur acconsentì a sottoporsi alle sue cure e, per ricompensa del trattamento positivo ricevuto, gli permise di consultare la biblioteca reale.
Purtroppo gli anni che seguirono non furono favorevoli per Ibn Sina, a causa delle lotte che si svilupparono per la supremazia in Asia centrale.

Avicenna scrisse circa 450 opere, delle quali circa 240 sono sopravvissute. Di queste 150 trattano di argomenti filosofici mentre 40 sono dedicate alla medicina. Questi sono i due campi nei quali si esercitò maggiormente il suo sapere. Ma egli scrisse anche di psicologia, geologia, matematica, astronomia e logica. Il suo più importante lavoro matematico fu un'immensa opera enciclopedica il Kitab al-Shifa, "Il libro delle cure". Una delle quattro parti del libro è dedicata alla matematica, in cui è trattata anche l'astronomia. Ibn Sina suddivideva l'astronomia in tavole astronomiche, tavole geografiche e calendario.
Eseguì anche osservazioni astronomiche, e sappiamo che alcune vennero eseguite a Isfahan e altre ad Hamadan. Inventò anche uno strumento astronomico mediante il quale era possibile osservare sia l'altezza di un astro che il suo azimut.

AL-ZARQALI (ARZACHEL)
Abu Ishaq Ibrahim ibn Yahya al-Zarqali (1028 - 1087). Conosciuto in Occidente con il nome di Arzachel, svolse la sua attività di astronomo a Toledo, principalmente con la compilazione delle famose Tavole toledane che acquisirono grande fama in Occidente dopo la loro traduzione in latino. Apportò molte correzioni a dati geografici che risalivano a Tolomeo e al al-Khwarizmi. Diede per il valore annuo del moto dell'apogeo solare il valore straordinariamente preciso di 12" di arco. A lui è attribuita l'invenzione di un particolare astrolabio che venne chiamato Safilah e che venne descritto in molte lingue.
Copernico esprime nel De revolutionibus la sua riconoscenza ad al-Battani e ad al-Zarqali.

AL-BITRUJI (ALPETRAGIUS)
Nur al-Din Ibn Ishaq al-Bitruji (ca. 1120 - 1204).
Originario del Marocco, emigrò in Spagna e visse principalmente a Siviglia. La sua opera principale fu Kitab al-Hayah che venne tradotta dapprima in ebraico e poi in latino. Tentò di apportare modifiche al sistema tolemaico, ma ne fu impedito dal volersi mantenere fedele ai canoni aristotelici di perfezione dei moti circolari.

AL-TUSI
Nasir al-Din al-Tusi (1201 - 1274) nacqua a Tus, nell'attuale Iran. Fu uno dei più grandi scienziati del suo tempo. Scrisse trattati di Algebra, aritmetica, trigonometria, fisica, geometria, logica, medicina, teologia. Venne protetto dal sovrano mongolo Hulug Begh che, impressionato dalla sua cultura (e probabilmente dalla sua abilità astrologica) lo nominò tra i suoi ministri.
Nel 1262 la munificienza del sovrano gli permise di costruire un osservatorio astronomico a Maragha e iniziò a sovraintendere all'attività di osservazione. L'osservatorio era dotato della migliore strumentazione, tra cui un quadrante murale di quaranta metri di raggio. Al-Tusi stesso progettò altri strumenti di sua concezione. Produsse delle tavole planetarie di straordinaria precisione ed un catalogo stellare, pubblicando il tutto con il titolo Al-Zij Ilkhani. Calcolò il valore di 51" quale rateo annuo della precessione degli equinozi. Fu forse il primo matematico a tentare di dimostrare il V postulato di Euclide, e fu anche tra i primi a mettere in evidenza notevoli improprietà nella dottrina tolemaica. In particolare si mostrò scettico sull'equante come punto rispetto al quale un moto non uniforme su un cerchio, poteva essere visto uniforme. In un'altra sua pubblicazione, Tadhkira Fi Ilm Al-Haya, "Memoria sull'astronomia", diede una versione critica della teoria tolemaica. Nello stesso libro propose un ingegnoso dispositivo che poteva essere usato nelle teorie planetarie: si trattava della dimostrazione che un moto oscillatorio rettilineo poteva essere prodotto dalla combinazione di due moti circolari (questo dispositivo oggi è spesso chiamato "la coppia di Al-Tusi"). Ciò era chiaramente in contrasto con la rigida distinzione operata da Aristotele tra i moti circolari uniformi (che erano riservati all'ambito delle sfere celesti) e i moti rettilinei (che erano propri del mondo sublunare).

I suoi studi di trigonometria sferica inclusero sei formule per la soluzione di triangoli rettangoli sferici. Fu il primo a trattare la trigonometria piana e sferica come una branca speciale della matematica.
Al-Tusi fu un prolifico scrittore. Sessantaquattro suoi trattati sono sopravvissuti e furono tutti tradotti in latino e nelle principali lingue europee.

LA TREPIDAZIONE
Diamo ora una descrizione sommaria della teoria della trepidazione perchè essa è attribuita, nella sua forma originale, a Thabit Qurra. Abbiamo visto che non appena l'astronomia araba, pur mantenendosi sostanzialmente nel solco della tradizione tolemaica, si avviò verso una sua autonoma operatività, non tardarono ad essere eseguite scoperte sensazionali, propiziate evidentemente da miglioramenti tecnologici strumentali di sette secoli, ma anche dalla autentica passione con cui gli Arabi si dedicarono a questa scienza. Abbiamo visto che Albatenio (che è considerato il più grande astronomo arabo) trovò per l'obliquità dell'eclittica il valore di 23º 33', ben più piccolo del valore ricevuto in eredità da Tolomeo di 23º 51' e che a lui fu dato di scoprire il moto dell'apogeo solare. Queste variabilità indussero purtroppo gli astronomi arabi ad ipotizzare la variabilità anche di un altro parametro astronomico, quello del valore annuo della precessione. Ciò fece nascere uno dei fantasmi dell'astronomia che imperversò poi per più di mezzo millennio, cioè la trepidazione

Le speculazioni degli Arabi si potevano riassumere grossolanamente così: tra l'epoca di Ipparco e quella di Tolomeo (circa 270 anni) la variazione della precessione appariva essere stata di circa 1º ogni 100 anni, mentre tra le osservazioni di Tolomeo e quelle arabe dei secoli IX e X, il rateo dava il valore di 1º ogni 66 anni. Contrariamente all'opinione del grande Al Battani che aveva saggiamente concluso che soltanto le accurate osservazioni dei secoli a venire avrebbero potuto stabilire se il rateo doveva essere considerato variabile o costante, nel secolo IX nacque la teoria della variabilità di entrambi i parametri, dell'obliquità e della precessione secondo un unico meccanismo. Per tradizione la teoria è attribuita a Thabit ibn Qurra (ca. 824 - 901), di cui abbiamo già dato alcune notizie.
Occorre ricordare che la teoria affondava nel passato. Teone di Alessandria, il commentatore di Tolomeo del secolo IV, nella sua introduzione alle Tabelle ridotte di Tolomeo, parla di una strana dottrina che veniva professata da antichi astrologi. Essi sostenevano che le stelle si muovevano, verso est per 8º al rateo di 1º ogni 80 anni. Dopo di che il moto si stabiliva verso ovest, sempre per 8º e sempre al rateo di 1º ogni 80 anni. Questo moto alternato continuava da tempo immemorabile. Inoltre, quegli astrologi fissavano all'anno 158 a.C. l'epoca nella quale il moto aveva cambiato direzione, stabilendosi verso est.

Occorre dire che né Tolomeo né alcun altro autore greco, tranne Teone di Alessandria, fece mai menzione di questa antica diceria. E' stata avanzata l'ipotesi che questa dottrina sia stata una erronea interpretazione del fatto che i Babilonesi ponevano, anticamente, l'inizio dei segni zodiacali equinoziali e solstiziali all'8º grado del rispettivo segno. Occorre anche dire che un semplice calcolo avrebbe dovuto mostrare, agli astronomi arabi del secolo IX che c'era qualcosa che non andava in quelle antiche teorie. Infatti, per eseguire uno spostamento di 8º al rateo di 1º ogni 80 anni, ci sarebbero voluti 640 anni e, se nel 158 a.C. era iniziato il movimento verso est, nell'anno 483 avrebbe dovuto aver luogo l'inversione, per cui al tempo di Thabit le stelle avrebbero dovuto essere in moto verso ovest, il che non era assolutamente vero: le osservazioni arabe mostravano inequivocabilmente che, almeno dal tempo di Ipparco, le stelle si erano sicuramente spostate di circa 14º verso est, senza alcuna inversione.

LA TREPIDAZIONE SECONDO THABIT
Nella cosmologia medioevale la sfera delle stelle fisse ricevette la denominazione di ottava sfera, perchè a Sole, Luna e ai cinque pianeti erano assegnate sette sfere. Il titolo latino dell'opera di Thabit che descriveva la trepidazione era Dei moti dell'ottava sfera.

Thabit si proponeva di fornire una spiegazione di due "fenomeni": la reale diminuzione dell'obliquità dell'eclittica, e la supposta variazione del rateo della precessione. All'uopo Thabit circondava l'ottava sfera con una ulteriore sfera, che nella cosmologia latina ricevette il nome di Primo mobile. Questa nona sfera era quella che comunicava alla sfera delle stelle fisse (e ai sistemi di sfere planetari interni di origine tolemaica) il moto diurno, e quindi era quella che portava l'equatore Q'RKQ. Questo equatore, fisso su questa sfera, era intersecato in un certo suo punto R dall'eclittica fissa E'RNME. Questa non era l'eclittica reale ma una fittizia, facente un angolo fisso di 23º 33' (secondo Thabit) con l'equatore del Primo mobile. PMKP' è il coluro solstiziale fisso. Nel punto R Thabit pone un cerchio, pure fisso, avente raggio angolare ampio 4º 18' 43". Un altro cerchio, simile al precedente, si trova centrato nel punto di equatore diametralmente opposto ad R. Lungo il cerchio centrato in R si muove di moto uniforme, nel senso indicato dalla freccia, il punto C, che gli astronomi latini chiamavano Caput Arietis.

BR>

(Questo punto C, pur muovendosi sul cerchio fisso di centro R, appartenente al Primo mobile, doveva intendersi (sempre secondo Thabit) appartenente all'ottava sfera).
Il moto uniforme di C era tale che l'angolo b variava di 360º in 4182 anni islamici (circa 4057 anni giuliani). Diametricalmente opposto a C c'è un punto, evidentemente anch'esso mobile con lo stesso ritmo di C, e detto dagli astronomi latini Caput Librae. Attraverso questi due punti passava l ' eclittica mobile CN (anch'essa appartenente all'ottava sfera). L'effettivo punto equinoziale primaverile ^ risultava dall'intersezione di questa eclittica mobile con l'equatore fisso.
L'eclittica mobile apparteneva dunque all'ottava sfera (assieme alle stelle fisse che sono appunto fisse su di essa), per cui il moto del punto C faceva muovere l'eclittica mobile e tutte le stelle della stessa quantità, onde la distanza angolare tra C e una certa stella che fosse capitata su questa eclittica mobile, sarebbe rimasta costante. Il punto N, di intersezione dell'eclittica mobile con la fissa, era sempre a 90º da C, ed era detto Caput Cancri. Esso aveva quindi un moto di avanti e indietro sull'eclittica fissa, e non era l'effettivo punto solstiziale, quello in cui il Sole vero raggiunge la massima declinazione (questo punto è indicato in figura con a.
Rispetto alla distanza dall'eclittica mobile quindi, la latitudine celeste rimane costante. La longitudine invece varia perchè la distanza angolare delle stelle dal punto ^ è continuamente variabile (come vedremo tra poco). Il moto di avanti e indietro delle stelle dell'ottava sfera implica una variazione di posizione delle stelle rispetto all'equatore della nona sfera, e quindi ascensione retta e declinazione saranno continuamente variabili.

ACCESSO E RECESSO DI THABIT
Volendo addentrarci (ancora per poco) nell'argomento trascendente della trepidazione, osserviamo la figura 12, che dà quattro situazioni del raggio RC, ad intervalli di 507 anni, durante i quali il detto raggio ruota di angoli b eguali di 45º. Come si vede, la distanza angolare della stella S dal Caput Arietis C rimane costante (è stata scelta una stella S giacente sull'eclittica mobile, per cui la sua latitudine rimane sempre zero). La longitudine di S, invece, essendo la distanza angolare di S da ^, varia in maniera irregolare. Si vede infatti che la longitudine aumenta di una quantità maggiore dall'anno 97 all'anno 604, di quanto non sia aumentata dall'anno 411 a.C. all'anno 97.
In ogni caso, la longitudine ^S è data da : ^S = CS + ^C, con CS costante come detto, e ^C positivo quando C è sopra l'equatore, e negativo quando è sotto. ^C (che, per un dato istante, ha lo stesso valore per tutte le stelle), nella teoria della trepidazione è detta equazione in longitudine.

Thabit non affrontò il problema di dare una formula trigonometrica per l'equazione in longitudine ^C. Diede una tabella di valori di ^C in funzione dell'angolo b, da 0º a 90º. I valori di questa tabella si accordano abbastanza bene con la formula sen(^C) = sen(10º 45')•sen(b), che venne largamente usata in seguito.

Dal De motu stellarum risulta chiaramente che Thabit era consapevole che questo moto alternativo produceva anche una variazione nell'obliquità, ma non si soffermò a trattare con calcoli questo aspetto, si limitò a dare alcuni valori. E' stato comunque calcolato recentemente che il modello di Thabit comportava una variazione dell'obliquità tra 23º59' e 23º29', che corrispondono proprio ai valori entro i quali l'obliquità era variata dall'antichità ai tempi di Thabit.
Eseguendo altri calcoli con formule più precise, si è determinato che il sistema di Thabit dava risultati in linea con ciò che si sapeva della precessione dai tempi di Ipparco. Infatti, secondo queste formule precise dall'epoca di Ipparco all'epoca di Tolomeo si avrebbe un rateo di 1º in 101 anni, mentre dall'epoca di Tolomeo fino all'epoca di Thabit il rateo sarebbe di 1º in 64º anni (ricordiamo che Thabit riteneva valido per il suo periodo il rateo di 1º in 66 anni).

LA TREPIDAZIONE NEI SECOLI SUCCESSIVI
Nel mondo islamico orientale questa teoria della trepidazione non venne accolta propriamente con favore. Al-Battani adottò un rateo uniforme di 1º in 66 anni (Thabit sostenne che in seguito anche al-Battani accettò la teoria). Ibn Yunus (1100) adottò un rateo costante di 1º in 70 anni, molto preciso per la sua epoca.
In Occidente ebbe un'accoglienza migliore. Le tabelle di Thabit vennero incluse nelle Tavole toledane e ciò contribuì enormemente alla popolarità della teoria stessa. A partire dal secolo XIII l'aumento costante della precessione avrebbe dovuto porre fine a qualunque idea di variabilità. Invece, nelle Tavole Alfonsine venne introdotta una teoria per la quale le stelle subivano una precessione costante che faceva loro compiere un giro completo di sfera celeste in 49000 anni, e a questo movimento costante veniva sovrapposta una oscillazione di ± 9º che si completava in un periodo di 7000 anni. Questa teoria, consacrata dalle Tavole Alfonsine divenne standard in Europa dal XIV al XVI secolo.

Era inevitabile che lo sdoppiamento della precessione venisse "spiegato" con l'introduzione di una ulteriore sfera (omaggio a Pitagora). L'illustrazione della Fig. 13 è tratta da un famoso libro, il Cosmographicus liber, scritto ed edito nel 1524 da Petrus Apianus (Peter Bienewitz, 1495 - 1552). La figura mostra al centro la Terra, circondata dalle sette sfere planetarie, a partire dalla Luna. L'ottava sfera, quella delle stelle fisse (nera), è chiamata Firmamento. La nona sfera, che Apiano chiama Cristallino, porta i due cerchi sui quali si muovono il Caput Arietis e il Caput Librae. Il cerchio del Caput Arietis è situato, correttamente, proprio prima dell'inizio della costellazione di Ariete. Notare come ci sia una piccola differenza tra l'inizio del segno di Ariete della nona sfera e l'inizio della costellazione di Ariete dell'ottava: questa differenza è attribuita alla componente variabile della trepidazione.

Invece la notevole differenza che c'è tra l'inizio dei due segni, della nona e della decima sfera (quest'ultima detta Primo mobile) indica l'effetto sulla precessione della componente fissa. Infine, anche Apiano, come Dante, circonda il cosmo con la sfera dell'Empireo, residenza di Dio e di tutti gli eletti. Anche in una edizione del Theoricae novae planetarum del famoso Georg Peurbach pubblicato a Parigi nel 1553, viene data la teoria originale della trepidazione di Thabit. Bisognerà attendere un astronomo dell'autorità di Tycho Brahe per togliere definitivamente la trepidazione dall'astronomia europea, alla fine del secolo XVI.