Meccanica celeste elementare





(Le nozioni esposte in questo capitolo sono finalizzate a dare al lettore - che lo desideri - una visione dei movimenti celesti tale da consentirgli di acquisire agevolmente anche gli argomenti degli altri capitoli).




RICHIAMI DI TRIGONOMETRIA PIANA
Riprendiamo alcune nozioni elementari di trigonometria piana.
Per un qualsiasi angolo a (fig. 1), si ha:
  • BC/AB = B'C'/AB' = B"C"/AB" = B'''C'''/AB''' = . . . = sen(a), " il seno dell'angolo a"
  • AC/AB = AC'/AB' = AC"/AB" = AC'''/AB''' = . . . = cos(a),
    "il coseno dell'angolo a"
  • BC/AC =B'C'/AC' = B"C"/AC" = B'''C'''/AC''' = . . . = tan(a), "la tangente dell'angolo a"
E' noto altresì che:
  • 1/sen(a) = cosec(a), "la cosecante dell'angolo a"
  • 1/cos(a) = sec(a), "la secante dell'angolo a"
  • 1/tan(a) = ctg(a), "la cotangente dell'angolo a"
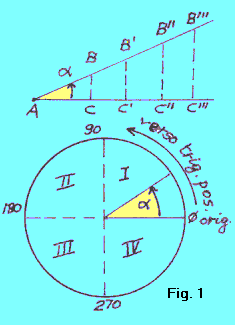Ricordiamo anche che nel cerchio trigonometrico, archi e angoli si misurano in:
  • gradi sessagesimali, cioè prendendo per angolo unitario la 360esima parte dell'angolo giro
  • radianti, cioè prendendo come angolo unitario la 2•pesima parte dell'angolo giro (un arco di lunghezza pari al raggio del cerchio stesso, perchè, come è noto, nella circonferenza sono contenuti 2•p raggi).
Essendo p = 3.14159265..., da 180º : p = aº : a(rad), si ha:
  • aº = a(rad) • 180/p     per passare da radianti a gradi
  • a(rad) = aº • p/180     per passare da gradi a radianti.
E' noto poi che, per convenzione, nel cerchio trigonometrico (fig. 1):
  • lo zero (origine) è posto a destra
  • il verso di percorrenza positivo, nella misura degli angoli, è antiorario
  • il cerchio è suddiviso in quattro quadranti denominati, a partire dallo zero, I, II, III e IV, rispetto al verso positivo

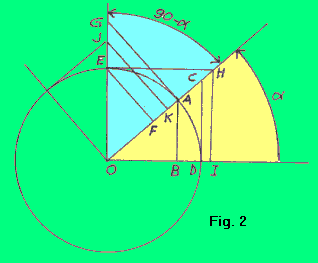
Esprimendo nel cerchio trigonometrico le lunghezze in radianti (cioè in raggi), la lunghezza del raggio (OE, OA, OD di fig. 2) ha valore 1.
Sono allora possibili (si osservi la figura 2) le seguenti semplificazioni (ricordiamo che il simbolo "==>" significa "implica"):
  • AB/OA = AB/1    ==>    AB = sen(a)
  • OB/OA = OB/1    ==>    OB = cos(a)
  • CD/OD = CD/1    ==>    CD = tan(a)
  • OD/CD = ctg(a)    ==> OI/HI = ctg(a)    ==>    OI = ctg(a)
  • OA/AB = cosec(a)    ==>    OH/HI = cosec(a)    ==>    OH = cosec(a)
  • OA/OB = sec(a)    ==>    OC/OD = sec(a)    ==>    OC = sec(a)
Essendo i tiangoli OAB e OEF uguali, si ha:
  • EF = OB    ==>    sen(90 - a) = cos(a)
  • OF = AB    ==>    cos(90 - a) = sen(a)
Essendo i triangoli OAG e OHI uguali, si ha:
  • AG = OI    ==>    tan(90 - a) = ctg(a)
Essendo i triangoli OKJ e ODC uguali, si ha:
  • OK = CD    ==>    ctg(90 - a) = tan(a)
Infine, poichè sen2(a) + cos2(a) = 1, si ha:
    sen(a) = [1 - cos2(a)]1/2     e     cos(a) = [1 - sen2(a)]1/2


Vediamo i segni delle funzioni seno, coseno e tangente.
A scuola abbiamo appreso che seno, coseno, tangente, ecc. vengono trattati come funzioni trigonometriche. Per quei lettori che avessero ricordi attenuati sull'argomento funzioni, diciamo che, nel loro studio, sull'asse orizzontale (figg. 3,4,5) viene riportata la lunghezza (detta variabile indipendente) dell'arco di circonferenza posto a sinistra di ogni figura, misurato a partire dallo zero, percorrendo il cerchio nel verso positivo. Sull'asse verticale, invece, viene riportato il valore della funzione vera e propria.
La funzione seno, fig. 3, varia entro la gamma di valori -1 <= y <= +1, positivi quando l'arco si trova nel I o nel II quadrante, negativi quando l'arco si trova nel III o nel IV quadrante
La funzione coseno, fig. 4, varia anch'essa entro i valori -1 <= y <= +1, positivi quando l'arco è nel I o nel IV quadrante, negativi quando è nel II o nel III quadrante.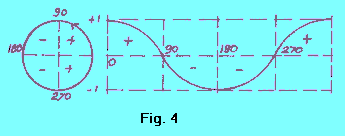
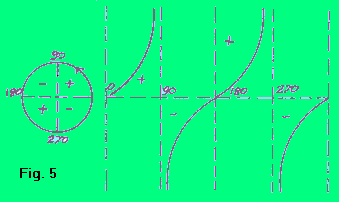
La funzione tangente, fig. 5, varia entro i valori < y < , positivi per il I e III quadrante, negativi per il II e il IV quadrante.


Vediamo le funzioni inverse delle funzioni seno, coseno e tangente.
La funzione arcsen è la funzione inversa della funzione sen. Ad esempio, considerando l'arco di 30º, la funzione "diretta" sen(30º) restituisce come è noto il valore 0.5. La funzione inversa arcsen(0.5) è quella che restituisce l'arco il cui seno vale 0.5, che sarà evidentemente l'arco di 30º (in radianti p/6). Diremo dunque che arcsen(0.5) = 30º = p/6 rad.
In trigonometria si fa anche uso delle funzioni arccos e arctan, funzioni inverse rispettivamente di cos e di tan.

Siccome arctan è l'unica funzione a trovarsi predefinita nella maggior parte dei linguaggi di programmazione, presentandosi talvolta la necessità di fare uso di arcsen e arccos, ricaviamo queste due funzioni a partire dalla arctan.

Considerando un arco qualsiasi y, si ha:
- arcsen[sen(y)] = y     (1)
- arccos[cos(y)] = y     (2)
- arctan[tan(y)] = y     (3)

Eguagliando i primi membri delle (1) e (3), sempre per un qualsiasi arco y, si ha:
arcsen[sen(y)] = arctan[tan(y)]
arcsen[sen[y)] = arctan[sen(y) / cos(y)]
Ponendo x = sen(y) e ricordando che sen(y) = [1 - cos2(y)]1/2, abbiamo:
arcsen(x) = arctan[x / (1 - x2)1/2]

Eguagliando invece i primi membri delle (2) e (3), per un qualsiasi arco y, si ha:
- arccos[cos(y)] = arctan[tan(y)]
- arccos[cos(y)] = arctan[sen(y) / cos(y)]
Ponendo x = cos(y) e ricordando che cos(y) = [1 - sen2(y)]1/2, abbiamo:
arccos(x) = arctan[(1 - x2)1/2 / x]
Queste due relazioni possono essere utili per quei lettori che hanno interesse per la programmazione.



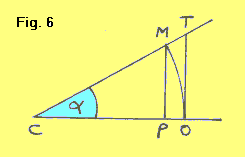
SENO E TANGENTE DI ARCHI PICCOLI
Sia OM = a un arco di cerchio (fig. 6). Sappiamo che: sen(a) = PM/CM, che tan(a) = OT/CO e che PM < a < OT. Indichiamo CM e CO con r, raggio del cerchio trigonometrico. Se l'arco a è molto piccolo possiamo ammettere, senza errore sensibile, che PM = a = OT. In queste condizioni, si può cioè dire che sen(a) = tan(a) = a/r.

In quest'ultima relazione a e r devono essere espressi nella stessa unità di misura, per esempio, entrambi in gradi, oppure entrambi in primi, oppure entrambi in secondi. Trattando solamente di secondi, il raggio (radiante) espresso in secondi è di 206265 secondi. Avremo dunque: sen(a) = tan(a) = a" / 206265".    (1)
Nel caso particolare in cui sia a" = 1" si ha: sen(1") = 1"/206265", per cui, in definitiva, la (1) diventa:
sen(a) = tan(a) = a" • (1"/206265") = a" • sen(1").


Ecco una breve nota sulla trigonometria sferica (fig. 7).
Anche nella trigonometria sferica vengono utilizzate le funzioni seno, coseno, tangente, ecc. della trigonometria piana. Poichè però qui si ha a che fare con superfici sferiche, le formule risolutive necessitano di alcuni adattamenti.
Una fondamentale differenza tra trigonometria piana e sferica è data dal fatto che in un triangolo sferico anche i lati sono angoli (archi). Precisamente, in un triangolo sferico (fig. 7), i lati sono, in genere, archi di cerchio massimo.



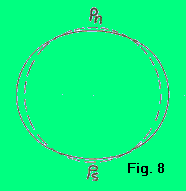
LA TERRA, LATITUDINE, LONGITUDINE
La forma della Terra è sferoidale, (fig.8). Rispetto alla pura forma circolare si ha uno schiacciamento ai poli e un rigonfiamento all'equatore. Il raggio medio è di circa 6300 Km. Ammettendo che la Terra sia una sfera, diciamo cerchio massimo qualunque cerchio di diametro uguale a quello terrestre. Tra i cerchi massimi sono notevoli i meridiani, che contengono i poli terrestri. Tra i meridiani è notevole quello passante per un osservatorio astronomico di una località presso Londra, Greenwich. Si dicono paralleli invece, i cerchi minori perpendicolari all'asse polare.
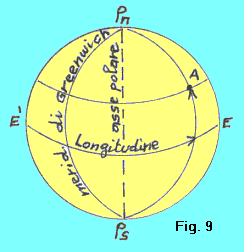
Latitdine di un punto A (fig. 9) è l'arco di meridiano compreso tra A e l'equatore. Si conta da 0º a 90º, a partire dall'equatore, verso nord e verso sud. Quindi si dice: latitudine 27º 35' 44" N, oppure latitudine 36º 28'.7 S, oppure latitudine 0 (per indicare un punto qualsiasi dell'equatore), oppure latitudine 90º N (per indicare il polo nord), oppure latitudine 90º S (per indicare il polo sud).
Longitudine di un punto A è l'arco di equatore compreso tra il meridiano di Greenwich e il piede del meridiano passante per A. Si conta da 0º a 180º a partire dal meridiano di Greenwich verso est o verso ovest. Quindi si dice longitudine 0, per indicare un punto qualsiasi del meridiano di Greenwich, oppure longitudine 48º 37' 22" E, oppure longitudine 128º 44'.7 W , oppure longitdine 180º, per indicare un punto qualsiasi dell'antimeridiano di Greenwich.



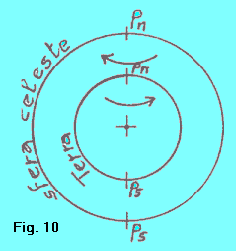
LA ROTAZIONE DELLA TERRA
Occorre definire in maniera precisa il senso secondo cui la Terra ruota (fig. 10). Per un osservatore che si trovi al polo nord e guardi la Terra sotto i suoi piedi, il senso della rotazione è antiorario. Per un osservatore che si trovi al polo sud e faccia la stessa cosa, il senso di rotazione è orario.
Un altro modo di definire il senso della rotazione terrestre è quello di fare riferimento al moto apparente giornaliero degli astri (fig. 11). Un osservatore che si trovi nell'emisfero terrestre nord, vede gli astri ruotare intorno al polo celeste nord in senso antiorario. Trovandosi invece nell'emisfero terrestre sud, vedrebbbe gli astri ruotare intorno al polo celeste sud in senso orario.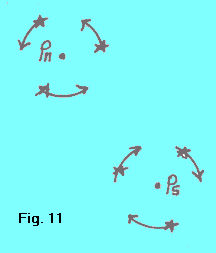
Si può fare riferimento al moto apparente giornaliero degli astri (Sole e Luna compresi), anche in altro modo (fig. 12). L'osservatore determina di trovarsi nell'emisfero nord se, volgendosi verso sud, vede gli astri muoversi in senso orario, sorgendo alla sua sinistra e tramontando alla sua destra. Determina di trovarsi nell'emisfero sud se, volgendosi verso nord, vede gli astri muoversi in senso antiorario, sorgendo alla sua destra e tramontando alla sua sinistra.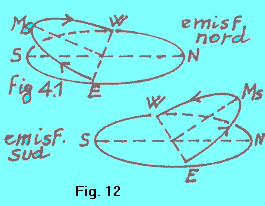



LA "SFERA CELESTE"
Prendiamo un punto qualsiasi O della superficie terrestre (fig. 13). La sua latitudine è data dall'arco QO, che corrisponde all'angolo ZCMs. Consideriamo il piano tangente alla superficie terrestre nel punto O (il lettore ammetterà che un'espressione come "superficie terrestre" è un'astrazione). Questo piano è detto orizzonte di O. La retta perpendicolere al piano, nel punto O, è detta verticale di O (è la direzione che in O assume il filo a piombo dei muratori). Il ramo di verticale diretto verso l'alto incontra la "sfera celeste" in un punto detto zenit di O. Il punto opposto allo zenit di O è detto nadir di O. L'intersezione con l'orizzonte di O del piano verticale passante per O (cioè contenente la verticale di O) e passante anche per i poli terrestri, determina sullo stesso orizzonte la linea meridiana nord-sud, n-o-s. La perpendicolare a questa linea, condotta per O, è detta linea est-ovest, e-o-w.
Per la enorme differenza tra:
- lunghezza del raggio della Terra
- "lunghezza del raggio della ipotetica sfera celeste"
possiamo senz'altro:
- trascurare il piano sopra definito orizzonte di O, (n-e-s-w)
- considerare al suo posto il piano parallelo al precedente, ma passante per il centro della Terra. Questo piano interseca la "sfera celeste" secondo un cerchio massimo (N-E-S-W), che è pure detto orizzonte di O (orizzonte celeste).
Questa semplificaziona equivale a ritenere nullo il raggio terrestre, cioè a ritenere la Terra puntiforme (nelle appresentazioni della "sfera celeste").

Il lettore avrà anche certamente compreso che la denominazione di "sfera celeste" è un'altra astrazione. E' dovuta unicamente al fatto che le grandissime distanze degli astri ci impediscono di percepire le differenze tra esse, per cui abbiamo l'illusione che tutti gli astri siano fissati, alla stessa distanza su una medesima lontanissima superficie sferica (gli Antichi la ritenevano addirittura reale). Nel seguito useremo l'espressione "sfera celeste" senza porla tra virgolette.
Un'importante osservazione che la figura ci consente è la seguente. Gli angoli ZCMs e PnCN, complementari dello stesso angolo ZCPn, sono eguali. Siccome ZCMs è, come detto in precedenza, la latitudine dell'osservatore, possiamo dire che l'altezza del polo celeste sull'orizzonte dà la latitudine dell'osservatore.





ALTRE DEFINIZIONI SULLA SFERA CELESTE
Tutti i piani contenenti l'asse del mondo Pn-Ps (fig. 14)intersecano la sfera celeste secondo cerchi massimi detti cerchi meridiani (oppure anche cerchi orari, oppure semplicemente orari). Tutti i piani contenenti la verticale dell'osservatore ZTN intersecano la sfera celeste secondo cerchi massimi, detti cerchi verticali (o semplicemente verticali). Il cerchio massimo Z-Ms-S-Ps-N-Mi-N-Pn è l'unico ad essere contemporaneamente orario e verticale: è detto meridiano dell'osservatore. Come meridiano è diviso in due semicerchi: quello contenente lo zenit, Pn-Z-Ms-S-Ps, è detto meridiano superiore (dell'osservatore), e quello contenente il nadir, meridiano inferiore.
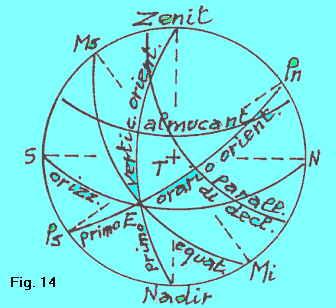Come cerchio verticale è pure suddiviso in due semicerchi, dei quali quello che contiene il polo celeste nord, Z-Pn-N-Mi-N, è detto verticale nord, e quello che contiene il polo celeste sud è detto verticale sud. I punti di intersezione dell'orizzonte con i verticali nord e sud sono detti rispettivamente punto cardinale nord e punto cardinale sud. Il piano passante per l'equatore terrestre interseca la sfera celeste secondo un cerchio massimo detto equatore celeste. I punti d'intersezione dell'equatore celeste con l'orizzonte sono i punti cardinali est e ovest. Il punto d'intersezione tra equatore e meridiano superiore, Ms, è detto mezzo cielo superiore. Dalla parte opposta c'è il mezzo cielo inferiore, Mi. I semicerchi orari passanti per i punti est e ovest sono detti primo orario, rispettivamente orientale e occidentale. I semicerchi verticali passanti per i punti est e ovest sono detti primo verticale, rispettivamente est ovest. Tutti i piani paralleli all'orizzonte intersecano la s.c. secondo cerchi minori, detti almucantarat. Tutti i piani paralleli all'equatore intersecano la s.c. secondo cerchi minori, detti paralleli di declinazione.



TRACCIAMENTO DELLA SFERA CELESTE
La procedura che esamineremo ci permette di tracciare la sfera celeste locale, per un osservatore posto a qualsiasi latitudine, in maniera geometricamente efficiente, intendendo con ciò dire che, con un minimo di segni grafici, lo schema che si ottiene ci fornisce tutte le informazioni di cui necessitiamo.
Precisiamo che la qualifica di locale si riferisce al fatto che questa rappresentazione della s.c. tiene conto della posizione geografica dell'osservatore, precisamente della sua latitudine. Vedremo in seguito che talvolta tracceremo s.c. nelle quali non si tiene conto della posizione dell'osservatore. Queste altre s.c. sono dette uranografiche. Ecco la procedura per la sfera locale (fig. 15):
  • Tracciare un cerchio di centro O, punto rappresentativo dell'osservatore e del centro della Terra.
  • Tracciare la verticale di O, ponendo sempre lo zenit Z in alto, e il nadir N in basso
  • Tracciare l'orizzonte di O, ponendo i due punti nord e sud, N e S, a piacere
  • A partire dal cardine nord (se la latitudine dell'osservatore è nord) o dal cardine sud (se la latitudine è sud), portare verso lo zenit un arco pari alla latitudine
  • Segnare i due poli, Pn e Ps, con Pn prossimo al punto N e Ps prossimo al punto S, e quindi tracciare l'asse del mondo Pn-Ps
  • Tracciare l'equatore, segnando correttamente i punti Ms, Mi, E, W (Ms prossimo allo zenit e Mi prossimo al nadir).
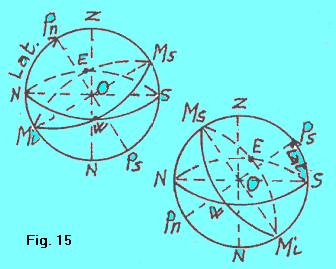C'è un altro modo di tracciare la sfera celeste locale, più semplice. Anzichè tracciare equatore ed orizzonte in maniera prospettica, come nella figura 15, essi vengono tracciati semplicemente come segmenti, NS per l'orizzonte e Ms-Mi per l'equatore, come nella figura 16 .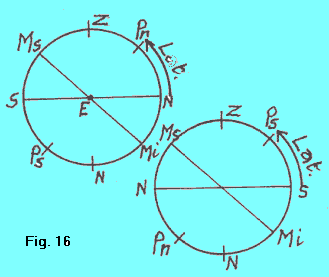



ESERCITAZIONI    (1)

  1. Tracciare le sfere locali secondo quanto appreso, per le seguenti latitudini:
    1. Latitudine 40º N
    2. Latitudine 30º S
    3. Latitudine 10º N
    4. Latitudine 10º S
    5. Latitudine 80º N
    6. Latitudine 80º S
    7. Latitudine 90º N
    8. Latitudine 90º S


  2. Indicare e calcolare l'espressione per la conversione dei seguenti valori angolari, risolvendola tramite calcolatrice (senza utilizzare il tasto <º'">). Dopo di che eseguire la stessa conversione tramite calcolatrice, (questa volta utilizzando il tasto <º'">).
    1. 312º 15' 35".79
    2. 244º 49' 17".1
    3. 128º 24' 49"
    4. 66º 16' 19"

      Soluzione per il caso (1):
      312º 15' 35".79 = (35.79 / 60 + 15) / 60 + 312
      Risolvendo quest'espressione tramite calcolatrice (senza far uso del tasto <º'">), otteniamo: 312.259941667
      Facendo uso del tasto <º'">, si ha subito:
      3, 1, 2, <º'">, 1, 5, <º'">, 3, 5, ., 7, 9, <º'"> ==> 312.259941667


  3. Eseguire manualmente le seguenti addizioni di valori angolari. Dopo di che controllare ogni risultato tramite calcolatrice (se un risultato è maggiore o uguale a 360º, togliere 360º):
    1. 277º 44' 53".44 + 98º 37' 22".37
    2. 12º 29'.8 + 3º 54'.7


  4. Eseguire manualmente le seguenti sottrazioni di valori angolari. Dopo di che controllare ogni risultato tramite calcolatrice (se un risultato è negativo, aggiungere 360º).
    1. 248º 25' 24".18 - 117º 44' 55".92
    2. 14º 35' 29".64 - 28º 12' 31"





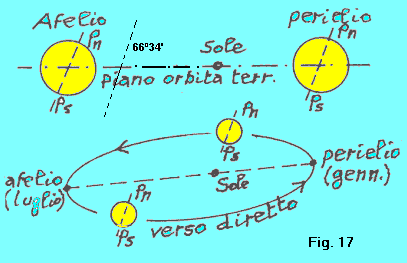
MOTO DI RIVOLUZIONE
La Terra ruota intorno al Sole nello stesso senso con cui ruota su sé stessa. Gli astronomi chiamano verso diretto il verso con cui avviene questo moto, e il verso contrario lo chiamano retrogrado (fig. 17).
Caratteristiche dell'orbita terrestre sono: (a) la ellitticità dell'orbita: il Sole è uno dei fuochi dell'ellisse. Di conseguenza, ci sarà un punto di massima distanza della Terra dal Sole (afelio, ai primi di luglio), e un punto di minima distanza (perielio, ai primi di gennaio). (b) la inclinazione dell'asse terrestre Pn-Ps rispetto al piano dell'orbita di circa 66º34'. Conseguenza di questa inclinazione dell'asse terrestre è la durata variabile del dì e della notte nel corso dell'anno.



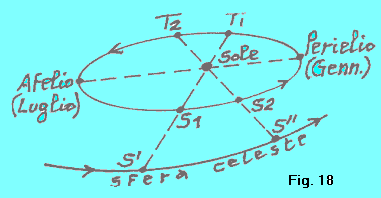
L'ECLITTICA
Mentre la Terra percorre l'arco T1-T2, (fig. 18), dalla Terra si vede il Sole, proiettato sulla sfera celeste, percorrere apparentemente l'arco S'-S", per cui si parla di moto apparente di rivoluzione del Sole intorno alla Terra (cioè il Sole sembra muoversi rispetto alle stelle fisse). Questo moto (apparente), fig. 18, avrà caratteristiche simili a quelle già viste per il moto terrestre (reale), cioè: (a) ellitticità dell'orbita apparente solare, (b) inclinazione dell'orbita stessa di 66º 34' circa rispetto al'asse terrestre.

Diremo allora che nel corso di quest'orbita apparente il Sole si trova all'apogeo (ai primi di luglio, quando in realtà è la Terra che si trova all'afelio), e che si trova al perigeo (ai primi di gennaio, quando in realtà la Terra si trova al perielio (fig. 19).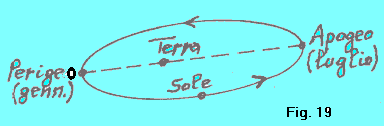

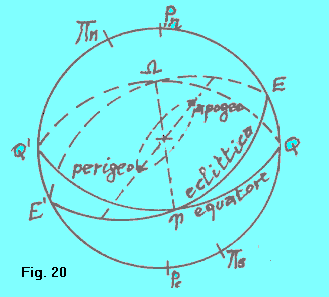
La proiezione di questa orbita solare apparente sulla sfera celeste è detta eclittica (fig. 20). Noi quindi vediamo il Sole muoversi apparentemente tra le stelle percorrendo l'eclittica nel corso di un anno. (Il lettore noti che l'inclinazione dell'orbita terrestre di 66º 34' rispetto all'asse terrestre, si traduce in definitiva in una inclinazione di circa 23º 26' dell'eclittica rispetto all'equatore, inclinazione che per tradizione è detta obliquità).
Si noti anche che così come il moto reale della Terra avviene nel senso diretto, definito precedentemente, anche il moto apparente del Sole sull'eclittica avviene in senso diretto. (La parola "diretto" si spiega con il fatto che per gli Antichi il moto del Sole era reale, e quindi al senso secondo il quale si compiva diedero la qualifica di "diretto", e "retrogrado" venne detto il senso contrario, che i pianeti assumevano talvolta).



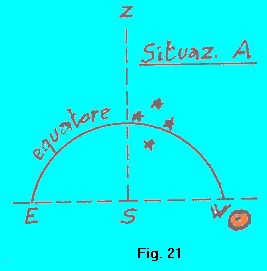
SVELARE IL "MOTO" DEL SOLE
Dunque il Sole ai nostri occhi appare muoversi tra le stelle fisse: precisamente, ad intervallo costante di un anno, "compie" un intero giro della volta celeste, percorrendo l'eclittica. Vediamo come possiamo renderci conto di questo (e come di ciò si resero conto gli Antichi).
Nella figura della situazione A è rappresentata una costellazione che è appena transitata al meridiano, nell'istante in cui il Sole è tramontato, diciamo, da un'ora. (La figura presenta, in maniera grossolana, la visione che si offre a un osservatore dell'emisfero terrestre nord, che volga lo sguardo verso sud).

Dopo un certo periodo di tempo, (un mese, due mesi), per un osservatore che si trovi nello stesso luogo e rivolga ancora lo sguardo verso sud, sempre un'ora circa dopo il tramonto del Sole, si avrà la situazione B, in cui si vede chiaramente che la distanza angolare tra la costellazione e il Sole si è ridotta. Siccome le due osservazioni sono avvenute allo stesso istante (un'ora circa dopo il tramonto) potremmo essere indotti a pensare che sia stata la costellazione (e quindi tutto il sistema delle stelle fisse) a muoversi verso ovest. Invece, come abbiamo detto nel paragrafo precedente, è stato il Sole, apparentemente, a muoversi, rispetto alle stelle fisse, verso est.

Dunque, il Sole si sposta verso est, rispetto a una stella fissa, di circa un grado ogni giorno. Inversamente, potremmo dire che una stella fissa anticipa il suo passaggio per uno stesso punto di cielo, rispetto al Sole, di circa quattro minuti al giorno. Quanto detto sopra spiega perchè, per una data località, una qualsiasi costellazione è visibile a un certo periodo dell'anno, a una certa ora, per esempio della sera, mentre a un altro periodo dell'anno è visibile a un'ora del mattino. Si noti, come detto precedentemente, che ciascuna stella della costellazione, malgrado questi diversi orari di visibilità, nel corso dell'anno percorre sempre lo stesso parallelo di declinazione.



LEVATA E TRAMONTO ELIACI
Questo argomento ha una grande importanza nello studio della storia dell'astronomia perchè la pratica delle osservazioni di levate e tramonti eliaci ha avuto grande applicazione presso tutte le comunità antiche. Vediamo dapprima cosa significa sorgere eliaco di un astro.
Abbiamo visto che una stella fissa, si rende visibile a ore diverse della notte durante l'anno, e ciò perchè il Sole si sposta apparentemente verso est tra le stelle. Supponiamo dunque che, a una data epoca dell'anno, un certo astro si trovi a levante del Sole di una ventina di gradi. Evidentemente, in queste condizioni l'astro non è visibile al mattino prima del sorgere del Sole, perchè si trova sotto l'orizzonte. Siccome il Sole si sposta apparentemente verso est di circa un grado al giorno, a un'epoca successiva si perverrà alla situazione in cui astro e Sole sorgono all'incirca contemporaneamente. Di nuovo, anche in queste condizioni l'astro non può essere visto al mattino. Continuando però il Sole a spostarsi verso est di un grado al giorno, verrà finalmente un giorno in cui la distanza angolare tra Sole e astro è diventata sufficientemente grande da far sì che l'astro sia visibile per pochi attimi, prima che il chiarore prodotto dal Sole che da sotto l'orizzote, si avvicina sempre più all'orizzote stesso, renda invisibile l'astro. Questa visione dell'astro è detta levata eliaca. Nei giorni successivi la visione dell'astro si farà sempre più distinta e durerà per un tempo sempre più lungo. Dunque, levata eliaca di un astro è quella situazione nella quale l'astro diviene visibile al mattino, nel cielo orientale, per la prima volta nel corso dell'anno, prima della levata del Sole.
Vediamo ora cosa significa tramonto eliaco di un astro. A mano a mano che ci si allontana dalla situazione di levata eliaca di un astro, abbiamo detto che, crescendo sempre più la distanza tra Sole e astro, l'astro stesso sorge sempre più anticipatamente rispetto al Sole, e conseguentemente tramonta sempre più anticipatamente. Ma procedendo sempre avanti nel corso dell'anno, si arriverà certamente a un'epoca nella quale l'astro sorge e tramonta dodici ore prima del Sole. A questo punto, il lettore stesso riconoscerà che: (1) la distanza angolare tra Sole e astro adesso tenderà a ridursi giorno dopo giorno, e (2) adesso è il Sole a tramontare ogni giorno prima dell'astro. E' evidente che finchè questo ritardo è di alcune ore, l'astro sarà visibile agevolmente nel cielo serale, dopo il tramonto del Sole, ma procedendo sempre il Sole verso est (cioè verso l'astro) di un grado al giorno, si arriverà a un giorno in cui la distanza tra Sole e astro è tale che, subito dopo il tramonto del Sole l'astro sarà visibile solo per pochi attimi, e nei giorni successivi non potrà più essere visto. Ebbene, quella situazione di visibilità dell'astro nel cielo serale per pochi attimi, è detta tramonto eliaco. Quindi, tramonto eliaco di un astro è quella situazione nella quale l'astro può essere visto nel cielo occidentale, dopo il tramonto del Sole, per l'ultima volta nel corso dell'anno. Già gli Antichi (sia i Babilonesi che i Greci, per esempio) si erano resi conto che le levate e i tramonti eliaci di determinati astri costituivano dei riferimenti temporali eccellenti rispetto all'anno solare (erano come pietre miliari posizionate lungo un certo percorso) e quindi potevano essere utilizzati per stabilire quando era tempo di eseguire determinati lavori agricoli. E' anche noto che la levata eliaca di Sirio era fondamentale per gli Egizi quale annuncio dell'inizio della piena del Nilo.



STRUTTURA DELL’ECLITTICA
Punti importanti dell’eclittica sono: (1) il punto ^ (gamma), detto anche primo punto d’Ariete, o anche punto vernale, o anche punto dell’equinozio di primavera. (2) il punto W (omega), detto anche punto dell’equinozio d’autunno. A 90º dai punti equinoziali si trovano i punti solstiziali, estivo e autunnale, rispettivamente E ed E’.

Il lettore noti che il verso astronomico diretto (verso del moto apparente del Sole lungo l'eclittica), mentre dall'emisfero nord terrestre (fig. 23a)è visto svilupparsi in senso antiorario (l'osservatore vede le costellazioni Ariete, Toro, Gemelli, ecc. susseguirsi in senso antiorario), nell'emisfero terrestre sud (fig. 23b) si sviluppa in senso orario (la stessa sequenza di costellazioni è vista svilupparsi in senso orario).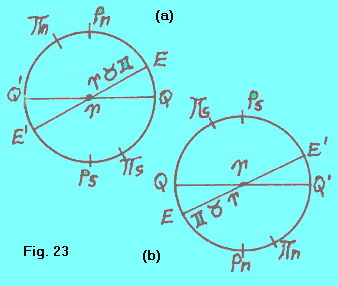



DURATA DEL DI’ E DELLA NOTTE DURANTE L’ANNO
Sull’orbita terrestre consideriamo le seguenti posizioni:
  • PSE - posizione solstiziale estiva
  • PEA - posizione equinoziale autunnale
  • PSI - posizione solstiziale invernale
  • PEP - posizione equinoziale primaverile

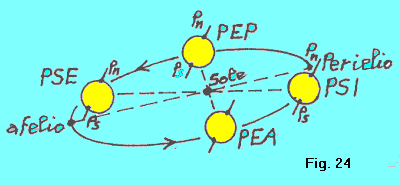Immaginiamo di porci con il punto di vista lungo la congiungente PEP-PEA, dalla parte di quest’ultima. Avremo la situazione di figura 25 (il Sole si trova sulla congiungente PSE-PSI “dietro” la posizione PEA.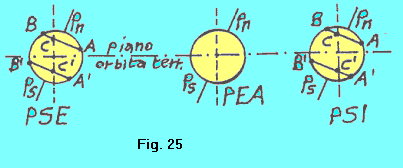

Nella posizione PSE (cioè al solstizio estivo) avviene quanto segue:
  • per un punto dell’emisfero terrestre nord che a causa del moto di rotazione percorra il parallelo ACB, l'arco di esposizione alla luce solare AC è maggiore dell'arco notturno BC
  • per un punto dell’emisfero terrestre sud che sempre a causa del moto di rotazione percorra il parallelo A’C’B’, l'arco di esposizione alla luce solare A’C’ è minore dell'arco notturno B'C'
Nella posizione PSI (cioè al solstizio invernale) si hanno conclusioni opposte a quelle di cui sopra.

Adesso immaginiamo di porci con il punto di vista lungo la direttrice PSI-PSE, dalla parte di quest’ultima. Otterremo la situazione di figura 26. Osserviamo che da questo punto di vista non siamo in grado di percepire l’inclinazione dell’asse terrestre rispetto al piano dell’orbita. Anche adesso il Sole si trova sulla direttrice PEP-PEA, “dietro” la PSE.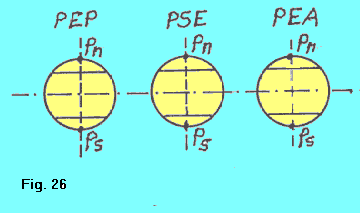

In questa situazione, vediamo che per entrambe le posizioni PEP e PEA (cioè agli equinozi) le lunghezze degli archi di esposizione alla luce eguagliano quelle dei rispettivi archi notturni, per qualsiasi punto della Terra. Possiamo concludere dicendo che:
  • per l’emisfero nord, mentre la Terra va dalla posizione PSI alla posizione PSE (dai primi di gennaio ai primi di luglio), la durata del dì è crescente e quella della notte è decrescente. Per l’emisfero terrestre sud si ha il contrario.
  • per l’emisfero nord, mentre la Terra va dalla posizione PSE alla PSI (dai primi di luglio ai primi di gennaio), la durata del dì è decrescente, mentre la durata della notte è crescente. Per l’emisfero sud si ha il contrario.
  • alle posizioni PEP e PEA (rispettivamente 21 marzo e 21 settembre circa, cioè agli equinozi), la durata del dì eguaglia quella della notte per qualsiasi punto della Terra. (Al polo nord il Sole sorge il 21 marzo (al polo sud il 21 settembre), rimane da allora sopra l’orizzonte fino al 21 settembre (al polo sud fino al 21 marzo), giorno in cui tramonta.



TEMPO CRONOLOGICO E SUA MISURA
Non siamo in grado di dare una definizione di tempo cronologico. Ci limitiamo a dire che il suo significato è intuitivo (primitivo). Potremmo dire che in determinati contesti, esso esplica la funzione di una coordinata cartesiana. Diciamo anche che nella presente trattazione non prendiamo in considerazione il concetto di tempo secondo la fisica relativistica. Ci limitiamo ala classica idea newtoniana di tempo assoluto (che “fluisce” in maniera uguale per tutti gli osservatori).
Vediamo come potremmo definire operativamente la nozione di simultaneità di due eventi. Diciamo che un modo per decidere se due eventi A e B siano o no simultanei (e nel caso non lo siano quale dei due precede l’altro), è quello di disporre di un moto continuo, quale quello eseguito da un punto materiale che percorra una certa traiettoria con moto uniforme, secondo un dato verso V (figura 27). Ragioniamo così: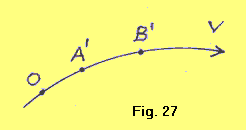
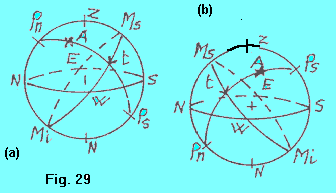
  • determiniamo la posizione A’ che il punto occupa simultaneamente all’evento A
  • determiniamo la posizione B’ che il punto occupa simultaneamente all’evento B
  • dalle posizioni di A’ e B’ rispetto al verso V, si decide se i due eventi sono stati simultanei, oppure se l’evento A ha preceduto l’evento B, o viceversa.
(Il lettore particolarmente attento potrebbe osservare che il ragionamento di cui sopra dovrebbe essere preceduto da una definizione non semplicemente operativa di simultaneità, ma noi diamo per scontato che non ce ne sia bisogno).
Un moto continuo del tipo anzidetto potrebbe essere costituito dal moto diurno di un astro A (figura 28). Il semicerchio orario dell’astro, Pn-A-Ps, forma, ad ogni istante, con il meridiano superiore dell’osservatore Pn-Z-Ms-S-Ps, un angolo, detto angolo orario, oppure anche tempo, t, dell’astro, che varia da 0º a 180º mentre l’astro percorre l’arco BAC, e da 180º a 360º mentre l’astro percorre il semiarco simmetrico “dall’altra parte del foglio”. Questo cerchio orario dell’astro si comporterà come una lancetta dell’orologio. Il tempo t, dell’astro (angolo orario), verrà misurato da 0º a 180º (da 0h a 24h), sull’equatore celeste, sempre a partire dal mezzo cielo superiore Ms, e sempre nel verso Ms-W-Mi-E

E’ opportuno che il lettore tenga presente che, poiché come appena detto, il verso secondo cui il tempo di un astro viene misurato è sempre secondo la successione Ms-W-Mi-E:
  • Nell’emisfero terrestre nord tale successione si sviluppa in senso orario (fig. 29a)
  • Nell’emisfero sud si sviluppa in senso antiorario (figura 29b)



ANGOLI ORARI SIMULTANEI DI UNO STESSO ASTRO
La figura 30 rappresenta la sfera celeste con punto di vista sull’asse del mondo Pn-Ps, dalla parte del Pn. Siano:
  • Pn-Zg il meridiano celeste corrispondente al meridiano di Greenwich
  • Pn-Ze il meridiano celeste corrispondente a un osservatore terrestre posto in una qualsiasi latitudine nord e longitudine est, data dall’arco Zg-Ze
  • Pn-Zw il meridiano celeste corrispondente a un osservatore terrestre di qualsiasi latitudine nord e longitudine ovest, data dall’arco Zg-W
  • Pn-A il meridiano (detto anche, come abbiamo appreso, cerchio orario) di un astro A.
Indichiamo con:
  • tAe, l’angolo orario dell’astro A, rispetto al meridiano Pn-Ze
  • tAw , l’angolo orario dello stesso astro, rispetto al meridiano Pn-Zw
  • T, l’angolo orario dello stesso astro, rispetto al meridiano di Greenwich Pn-Zg Precisando bene che i tre angoli orari sono simultanei, cioè sono misurati contemporaneamente da tre osservatori diversi (uno a est, uno a ovest e un terzo sul meridiano di Greenwich), si hanno le relazioni:
        tAe = T + Longit. est,     tAw = T - Longit. ovest
    che possono essere compendiate nell’unica relazione :
         t = T + Long
    da cui derivano le relazioni : T = t - Long. e Long = t - T
    tutte e tre da considerare algebriche, cioè in esse la longitudine dev’essere considerata una quantità positiva se est e negativa se ovest.



RELAZIONE FONDAMENTALE TRA TEMPO DI UN ASTRO E SIMULTANEO TEMPO SIDERALE
Il punto ^, uno dei due punti di intersezione tra equatore celeste ed eclittica, ha sempre avuto, fin da tempi antichissimi, una grande importanza in astronomia. Ancora oggi è considerato dagli astronomi “come se fosse una stella come tutte le altre”. Addirittura, l’angolo orario di questa stella fittizia viene tabulato nelle effemeridi (per le effemeridi nautiche ,Nautical Almanach, la tabulazione è per ogni ora). L’angolo orario di questa stella fittizia è detto tempo sidereo e si indica di solito con ts, se riferito a un meridiano qualsiasi, e Ts se riferito al meridiano di Greenwich (gli inglesi lo indicano con SHA, Sideral Hour Angle). Quindi, tanto il punto ^ quanto una stella qualsiasi, compiono un giro della sfera celeste (naturalmente ciascuno sul proprio parallelo di declinazione, (che per il punto ^ come detto è l’equatore celeste) nello stesso tempo, cioè in 24 ore di tempo siderale.
Nella figura 31, la solita sfera celeste vista da “sopra” il polo celeste nord, tanto il punto ^ che un astro qualsiasi A, verrebbero “visti” ruotare in senso orario (in effetti, la Terra, sotto di essi, verrebbe vista ruotare effettivamente in senso antiorario). Nel ruotare, punto ^ e astro A si mantengono a una distanza angolare praticamente costante che è detta ascensione retta dell'astro A, indicata di solito con a. Le ascensioni rette degli astri si contano da 0º a 360º, sempre a partire dal punto ^, e in senso antiorario rispetto a un osservatore che guardi la sfera celeste da sopra il polo nord.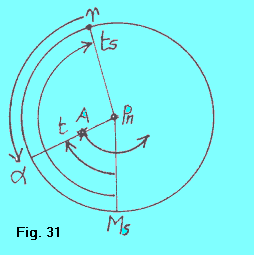

In un istante qualsiasi si hanno i seguenti angoli:
  • t, angolo orario dell’astro, contato sempre a partire dal mezzo cielo superiore Ms (in questo caso in senso orario perché l’osservatore si trova nell’emisfero nord e la sua sfera celeste ha come polo elevato il Pn)
  • ts, tempo sidereo, angolo orario del punto ^, quindi contato anche lui a partire dal Ms, come si contano gli angoli orari, cioè in questo caso in senso orario perché il polo elevato è il polo nord.
  • a, ascensione retta dell’astro, sopra definita.
Fra i tre elementi di cui sopra esiste la relazione:     ts = t + a

Questa relazione può ritenersi valida per tutti gli astri, anche per i cosiddetti astri erranti (Sole, Luna, pianeti, satelliti, ecc.) purchè, per questi ultimi, l’ascensione retta sia riferita all’esatto istante considerato. Per le stelle fisse invece l’ascensione retta è praticamente costante per lunghi periodi di tempo (su questo punto saremo più precisi in seguito).



MISURA DEL TEMPO CON IL TEMPO SIDEREO
Ammettiamo che la rotazione della Terra attorno al proprio asse si compia:
- con durata costante di una intera rotazione
- con velocità angolare uniforme
(Da una cinquantina d’anni è stato definitivamente accertato che nessuna delle due ipotesi è vera: la rotazione terrestre si compie con lievissime irregolarità, imprevedibili nel lungo periodo. Noi comunque, in questa fase della nostra disanima, ammettiamo che le due ipotesi siano vere).
Poiché la rotazione apparente della sfera celeste riproduce esattamente (salvo il verso) la rotazione della Terra, si potrebbe pensare di utilizzare il moto in angolo orario di una stella per misurare il tempo. Anziché una stella qualsiasi, i fisici hanno scelto il punto ^: la ragione di ciò sta nel fatto che detto punto riveste una grande importanza in astronomia, essendo l’origine per la misura di coordinate uranografiche celesti degli astri (ad esempio, come abbiamo visto, l’ascensione retta).

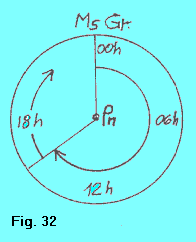
Si costruiscono perciò speciali cronometri (con quadranti graduati generalmente da 0h a 24h), che riproducono esattamente il moto del punto ^, vale a dire che essi segnano esattamente 00h 00m 00s nell’istante in cui il detto punto transita al meridiano superiore. Sono detti cronometri siderei, e l’ora da essi segnata è detta ora siderea (o anche tempo sidereo). Inoltre, quale meridiano di riferimento per tutti i cronometri siderei (di tutto il mondo), si è scelto il meridiano di Greenwich, per cui il valore orario letto a un cronometro sidereo si indica con il simbolo Ts.

E’ interessante notare che (figura 32) un quadrante di un cronometro sidereo può essere riguardato come una proiezione ortografica equatoriale dell’emisfero nord della sfera celeste (una sfera celeste rappresentata nel modo visto dianzi, con punto di vista sull’asse del mondo, dalla parte del polo nord celeste). Il raggio (arbitrario) tracciato sul quadrante, a partire dal centro, fino alla graduazione 00h rappresenta il meridiano di Greenwich.



NECESSITA’ DI UN ALTRO TIPO DI TEMPO
Il tempo sidereo è usato in non poche attività scientifiche e tecniche (osservatori astronomici, navigazione marittima, aerea, ecc.) Il suo uso nella vita corrente presenterebbe però inconvenienti di non lieve entità. Le attività umane sono regolate, in senso lato, sul moto in angolo orario del Sole. Ad esempio, è un istante importante quello in cui l’angolo orario del Sole (Sole vero) è 00h 00m 00s (o anche 00º00’00”) che si chiama mezzodì vero (istante della giornata in cui il Sole raggiunge il punto più alto). Se nella vita ordinaria si usasse misurare il tempo con un cronometro sidereo, agli istanti predetti corrisponderebbero ore sideree variabili giornalmente di quattro minuti circa, e quindi variabili durante l’anno, il che costituirebbe un inconveniente pratico non trascurabile.

Sorge quindi la necessità di abbandonare il tempo sidereo per gli usi della vita quotidiana, e di riferirci invece per la misura del tempo, al Sole, sul quale sono, come detto, regolate la gran parte delle attività umane. Ma non possiamo servirci del moto in angolo orario del Sole perché questo moto non è uniforme. Infatti, non è uniforme il moto in angolo orario di un qualsiasi astro che non sia una stella fissa. In particolare, la non uniformità del moto del Sole discende da:
  • non uniformità del moto di rivoluzione della Terra intorno al Sole (la velocità non costante di rivoluzione della Terra intorno al Sole, implica una non costanza nella variazione giornaliera in ascensione retta del Sole, e quindi una non costanza del moto in angolo orario del Sole)
  • dal punto precedente deriva la durata sempre diversa dell’intervallo di tempo tra due passaggi consecutivi del Sole allo stesso meridiano. Il Sole vero, quindi, (quello con cui abbiamo a che fare tutti i giorni), non è adatto alla misura del tempo perché non ha un moto uniforme in angolo orario.



IL TEMPO MEDIO
E’ detto Sole vero l’astro che percorre l’eclittica in un intervallo di tempo detto anno tropico con moto che sappiamo essere non uniforme (leggi di Keplero). Abbiamo visto che per la misura del tempo avremmo bisogno di un astro che percorresse l ‘ equatore celeste con moto uniforme, perché allora avrebbe un moto uniforme in ascensione retta e quindi in angolo orario. Gli astronomi hanno introdotto due soli immaginari, uno detto Sole fittizio e l’altro Sole medio. Riferiamoci alla figura 20. Il Sole fittizio percorre l’eclittica con moto uniforme, transitando assieme al Sole vero al perigeo e all’apogeo. Il Sole medio, invece, percorre con moto uniforme l’equatore celeste, transitando al punto ^, ogni anno, cioè ogni 365.2422 giorni solari medi, assieme al Sole fittizio. Quest’ultimo non è adatto alla misura del tempo perché non percorre l’equatore con moto uniforme. Il Sole medio, invece, fa questo e quindi è adatto alla misura del tempo. (Naturalmente il lettore deve intendere la frase “percorre l’equatore con moto uniforme” nel senso che gli astronomi hanno tabulato la sua posizione sulle effemeridi in modo che si muova con moto uniforme).

Allora, associato al concetto di Sole medio, è stato introdotto anche il concetto di giorno solare medio: esso ha durata risultante dalla media aritmetica di un gran numero di giorni solari veri. Poiché l’anno tropico è, come detto sopra, di 365.2422 giorni solari medi, in un giorno medio l’ascensione retta del Sole medio varia di: 24h / 365d.2422 = 86400s / 365d.2422 = 236s.56 = 3m 56s.56

Diciamo allora che giorno solare medio è l’intervallo di tempo che intercorre tra due transiti consecutivi del centro del Sole medio allo stesso meridiano. E diciamo anche che tempo solare medio, oppure tempo medio, oppure ora media è l’angolo orario del Sole medio. Quindi, l’astro adottato per la misura del tempo è il Sole medio (astro fittizio), e l’angolo orario di questo astro, detto tempo medio, viene usato per la misura corrente del tempo.



TEMPO MEDIO CIVILE
Si costruiscono dunque orologi, cronometri, pendoli, ecc. regolati sul tempo medio (tempo relativo all’astro fittizio denominato Sole medio). Gli orologi della vita di tutti i giorni sono appunto regolati sul tempo medio: forniscono, ad ogni istante, l’angolo orario del Sole medio, tm, così indicato se il meridiano a cui è riferito è un meridiano qualsiasi. Se invece il meridiano a cui è riferito è il meridiano di Greenwich, allora l’ora media si indica con Tm, oppure talvolta anche con GMT (Greenwich Mean Time).

Il lettore prenda nota che gli angoli orari del Sole medio, per universale convenzione, si contano a partire dal meridiano inferiore dell’osservatore (figura 33 a,d). Tale modo di contare gli angoli orari è detto modo civile, per distinguerlo dal modo astronomico, riservato per tutti gli altri astri (compreso il Sole vero), per i quali i tempi si contano, come già detto, a partire dal meridiano superiore (fig. 33 c). In pratica, quanto appena detto si riduce al fatto che, quando un astro qualsiasi (tranne il Sole medio) transita al meridiano di una località qualsiasi, si dice che il suo angolo orario è 0º, oppure 0h (tempo vero tv = 0º = 0h , fig. 33 c), mentre quando a passare al meridiano di una località qualsiasi è il Sole medio (fig. 33 d), si dice che in quell’istante il suo angolo orario è 180º, oppure 12h (tempo medio tm = 180º = 12h).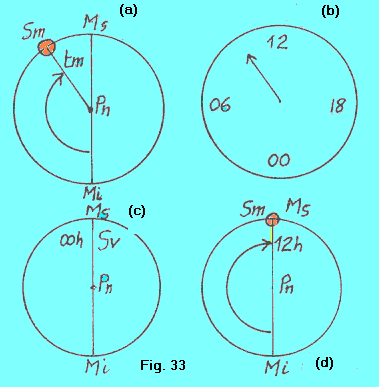



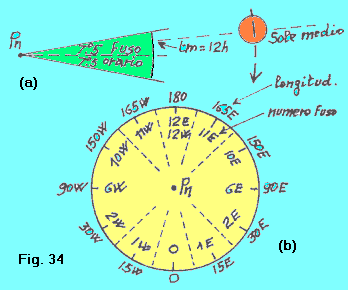
IL REGIME DEI FUSI ORARI
E’ evidente che tutti gli orologi di una nazione devono essere regolati rispetto a uno stesso meridiano, ed è altrettanto evidente che questo meridiano dev’essere scelto con un certo criterio. Per disciplinare le relazioni di tempo cronologico tra le varie nazioni, queste hanno aderito da molti anni alla Convenzione sui fusi orari. Per essa, la superficie terrestre è stata suddivisa in 24 fusi, ampi ciascuno 15º, e numerati da 0 a 12, verso est e verso ovest (figura 34 b). Tutte le nazioni che capitano all’interno di uno stesso fuso (seguendo naturalmente i confini politici) avranno i propri orologi regolati sul meridiano centrale del fuso. Ad esempio, in Italia, che cade nel fuso 1 (fuso dell’Europa Centrale), gli orologi sono regolati rispetto al meridiano 15º E (1h E), per cui si dice che l’Italia ha tempo fuso tf = 1 est, cioè GMT + 1.

Durante i mesi estivi poi (in Italia e in quasi tutta Europa dall’ultima domenica di marzo all’ultima di ottobre), quasi tutte le nazioni adottano la cosiddetta ora estiva, cioè le lancette dell’orologio vengono avanzate di un’ora (quindi in Italia si ha allora GMT + 2). Osserviamo a questo proposito che da molte persone l’ora estiva viene impropriamente chiamata “ora legale”. Questo termine è chiaramente improprio perché l’ora adottata da qualunque nazione è sempre legale, nel senso che è sempre imposta per legge.



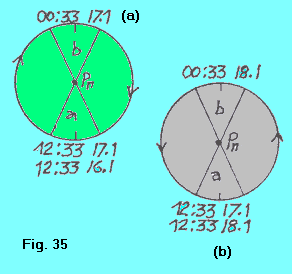
LINEA DEL CAMBIAMENTO DI DATA
I provvedimenti presi durante la conferenza sui fusi orari non si limitarono all’adozione dei 24 fusi. Se così fosse stato, si sarebbero avuti notevoli inconvenienti.
Per rendersi conto di ciò, si osservi la figura 35 a. Supponiamo che nel fuso “a” l’orario sia le 12.33 del 17.1. Percorrendo la Terra in senso orario, dobbiamo attribuire al fuso “b”, opposto ad “a” l’orario simultaneo 00.33 dello stesso giorno 17.1. E da là continuando a percorrere la Terra in senso orario, arrivati di nuovo ad “a” gli dobbiamo attribuire l’orario simultaneo 12.33 del 16.1, in contrasto con l’orario di partenza.
Anche se, sempre partendo dal fuso “a”, percorriamo la Terra in senso antiorario, figura 35 b, quando ritorniamo al fuso “a” ci ritroviamo con un orario simultaneo sfasato di 24h rispetto a quello di partenza.

Si dovette evidentemente trovare una soluzione per questo problema, soluzione che venne individuata con l’introduzione della linea del cambiamento di data, che, per convenzione, venne stabilita all’antimeridiano di Greenwich (con le opportune modifiche) Si osservi la figura 36. Se per esempio nel fuso “a” sono le 12.04 del 20.1, nel fuso “b”, fuso di Greenwich, saranno contemporaneamente le 06.04 del 20.1, nel fuso “c” saranno contemporaneamente le 00.04 del 20.1, e finalmente nel fuso “d”, fuso dell’antimeridiano di Greenwich, saranno per tutta l’estensione del fuso le 18.04, ma nella metà orientale le 18.04 del 20.1 e in quella occidentale le 18.04 del 19.1. Evidentemente, la linea del cambiamento di data non taglierà una stessa nazione in due, ma seguirà i confini politici in modo da lasciare l’intera nazione in un semifuso o nell’altro (come del resto avviene nella separazione di un fuso qualsiasi da quello adiacente).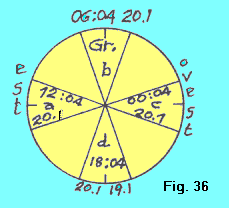

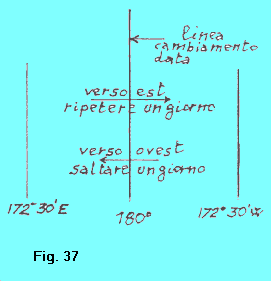
Le navi e gli aerei che attraversano l’antimeridiano di Greenwich, dovranno (figura 37):
  • ripetere (il giorno dopo) la data di attraversamento, se navigano verso est
  • saltare (il giorno dopo) a una data maggiore di un giorno, se navigano verso ovest.

Si ebbe a che fare con problemi di ripetizione o di salto di data soltanto con il primo viaggio di circumnavigazione del globo. A. Pigafetta (1485 - 1534), nella sua relazione sul viaggio della spedizione di Magellano (Fernando Magalhaes, 1480 - 1521), descrive lo stupore provato dall’equipaggio della nave Victoria (unica superstite del gruppo di cinque navi partite da Huelva, al comando di Magellano, con rotta verso ponente) all’arrivo alle isole del Capo Verde (quindi al termine della circumnavigazione), quando si sentirono dire che la data colà era giovedì 10 luglio, mentre, secondo le osservazioni dei loro libri di bordo (di cinque anni), avrebbe dovuto essere mercoledì 9 luglio. Nemmeno nelle università europee si fu in grado di fornire subito una spiegazione accettabile. Questa fu data qualche tempo dopo da P. M. d’Anghiera (1456 - 1526). Mentre al porto di partenza e a Capo Verde, durante l’assenza della nave erano trascorsi X giorni (cioè il Sole era transitato X volte sopra Capo Verde), sopra la nave Victoria il Sole era transitato X - 1 volte, perché la nave stessa aveva compiuto un giro del mondo nella stessa direzione del Sole (cioè verso ponente), per cui i marinai della Victoria avevano registrato X - 1 giorni.




ESERCITAZIONI     (2)

  • Dati i seguenti angoli orari rispetto a Greenwich, calcolare gli angoli orari riaspetto alle longitudini indicate (dopo aver eseguito ogni calcolo manualmente, controllarne l'esattezza tramite calcolatrice). Illustrare anche ogni calcolo con il corrispondente schema grafico:
    • T = 18º 47'.7, LONG = 177º 25'.2 E (grafico per emisfero nord)
    • T = 229º 34'.5, LONG = 48º 12'.5 W (grafico per emisfero sud)
    • T = 317º 25'.4, LONG = 115º 17'.2 E (grafico per emisfero nord)
    • T = 136º 48'.9 LONG = 45º 28'.9 w (grafico per emisfero sud)


  • Per ognuno degli astri che seguono, dei quali sono date le ascensioni rette a, calcolare i valori di tempo locale t, per l'istante astronomico comune ts = 235º 27'.4.
    Illustrare ogni calcolo con il corrispondente schema grafico.
    • Vega : a = 278º 51'.8 (grafico per emisfero nord)
    • Antares : a = 246º 40'.5 (grafico per emisfero sud)
    • Aldebaran : a = 68º 55'.0 (grafico per emisfero nord)
    • Sirio : a = 101.14.1 (grafico per emisfero sud).





MOTO APPARENTE DIURNO DELL’ECLITTICA
Riteniamo utile per il lettore questo paragrafo che gli consente di acquisire il “moto apparente diurno” dell’eclittica. Come già detto, l’eclittica è quella linea immaginaria che il Sole appare percorrere sulla volta celeste, ritornando all’equinozio di primavera ogni 365.2422 giorni solari medi. Non essendo dotata di materialità, non avrebbe senso parlare di “moto apparente diurno dell’eclittica”. Lo facciamo unicamente affinchè il lettore "veda" come avviene il suo moto. Constateremo in seguito, invece, che per le costellazioni dell’eclittica ha senso parlare di moto apparente diurno, perché esse sorgono, passano al meridiano e tramontano come le altre costellazioni.

La figura 38 mostra una particolare posizione dell’eclittica: quella che si ha all’istante del sorgere del punto ^. Se immaginiamo che tutti i punti dell’eclittica siano stelle (come abbiamo immaginato lo sia il punto ^), allora i percorsi che verranno eseguiti nel cielo da ciascun punto saranno quelli indicati dalle linee tratteggiate.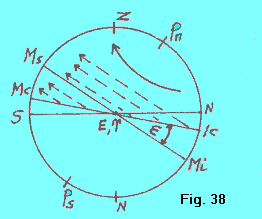

Potrebbe darsi che quanto detto or ora non sia sufficiente per far acquisire al lettore il moto dell’eclittica. In tal caso gli suggeriamo di riferirsi alla figura 39. Immagini il lettore di tracciare su quel mappamondo (rappresentativo della sfera celeste) un cerchio massimo e-e’, che formi un angolo di circa 23º26’ con l’equatore q-q’. Dopo di che, inclinando l'asse del mappamondo, rispetto alla orizzontale, di un angolo pari (all'incirca) alla latitudine locale e facendo ruotare il mappamondo nel senso indicato dalla freccia (senso del moto apparente della sfera celeste), avrà una cognizione più chiara del moto diurno dell’eclittica. Riferendo il detto moto a una linea orizzontale, rappresentativa dell’orizzonte di quella sfera celeste, il lettore vedrà chiaramente che si tratta di un moto che potrebbe definirsi “sbilenco” (dovuto al fatto che, ruotando la sfera celeste, l’eclittica taglia l’orizzonte con una angolatura continuamente variabile).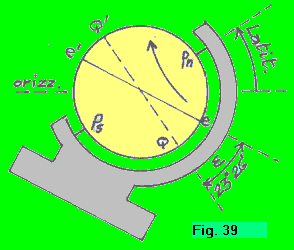

Diamo ora un minimo di terminologia riguardante l’eclittica. Le figure indicano la posizione dell’eclittica per un certo istante della giornata siderale, precisamente per l’istante in cui l’angolo orario del punto ^ è 120º. Si dice discendente il punto istantaneo (continuamente variaile)di eclittica in cui questa incontra l’orizzonte occidentale. Nelle figure è indicato con DSC. ascendente è invece detto il punto istantaneo di eclittica che incontra l’orizzonte orientale (gli Antichi lo chiamavano oroscopo). In figura 41 è indicato con ASC.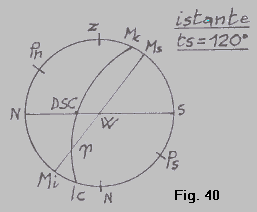

Il punto istantaneo di incontro dell’eclittica con il meridiano superiore è detto mezzo cielo. Il punto istantaneo di incontro dell’eclittica con il meridiano inferiore è detto fondo cielo. Sono indicati rispettivamente con Mc ed Ic. Variando continuamente la giacitura dell’eclittica, questi due punti oscillano continuamente lungo il meridiano. Per la stessa ragione, ASC e DSC oscillano continuamente sull’orizzonte rispetto ai punti cardinali est e ovest.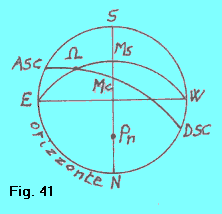


LO ZODIACO
Gli astronomi dell’antichità, per meglio prendere nota degli spostamenti del Sole durante l’anno, raffigurarono alcuni gruppi di stelle, precisamente quelle costellazioni che individuarono in una fascia sferica estendentesi circa 8º a nord e a sud del percorso del Sole stesso. Fissarono la loro attenzione su quella fascia perché nel suo ambito, come vedremo in seguito, notarono che alcune stelle, contrariamente a tutte le altre, presentavano degli strani moti, per cui vennero denominate pianeti, (letteralmente “astri erranti”).

L’insieme di quelle costellazioni costituisce lo zodiaco. I nomi delle costellazioni, a partire dal punto ^ e procedendo nello stesso senso del Sole lungo l’eclittica, nell’antichità erano: Ariete (^), Toro (_), Gemelli (`), Cancro (a), Leone (b), Vergine (c), Bilancia (d), Scorpione (e), Sagittario (f), Capricorno (g), Acquario (h), Pesci (i).



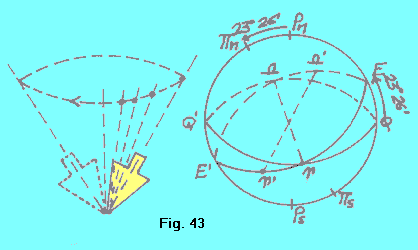
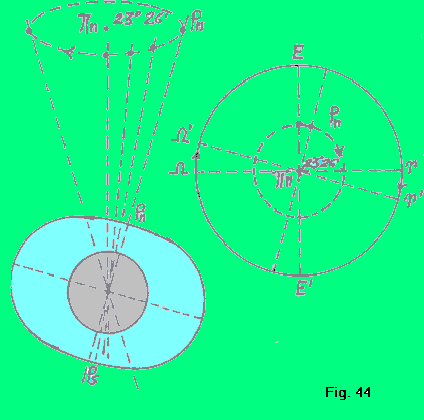
PRECESSIONE DEGLI EQUINOZI
Si ritiene che le azioni gravitazionali sulla Terra di Sole e Luna (evidentemente disuguali), agendo sul rigonfiamento equatoriale terrestre (che in figura 44 è stato molto esagerato), facciano in modo che l’asse di rotazione terrestre, pur mantenendo costante la sua inclinazione rispetto al piano dell’eclittica, compia attorno all’asse dell’eclittica, pn-ps, un lentissimo movimento “a trottola a bassa velocità”, descrivendo un cono, con angolo al vertice di circa 23º26’ in circa 25.800 anni.

Il piano dell’equatore terrestre, pur conservando anch’esso costante la sua inclinazione rispetto al piano dell’eclittica, è ovviamente coinvolto in tale moto. Il risultato di ciò è che le intersezioni dell’equatore con l’eclittica (i punti ^ e W), la cui congiungente è detta, come abbiamo visto, la linea degli equinozi, ruota attorno al suo centro O, mantenendosi evidentemente sempre nel piano dell’eclittica. Questo moto è retrogrado (contrario al senso del moto del Sole sulla stessa eclittica) ed ha lo stesso periodo di 25.800 anni.
Il fenomeno, che ovviamente può essere riscontrato solo in rapporto alle stelle fisse, è conosciuto con il nome di precessione degli equinozi (o anche di retrogradazione dei nodi). L’entità annuale di tale movimento è di 50”.25.



RETROGRADAZIONE DEI NODI
La scoperta del fenomeno è attribuita all’astronomo greco Ipparco da Nicea, il quale, intorno all’anno 128 a.C. determinò che tutte le stelle fisse avevano aumentato la loro longitudine di circa due gradi, rispetto alle misure eseguite circa 150 anni prima da altri astronomi greci. Fu lui a chiamare il fenomeno precessione, e ne stabilì l’entità in circa 45” all’anno (misura di grande precisione per quell’epoca).

Una conseguenza immediata di questo fenomeno è che le costellazioni dello zodiaco che, ai tempi di Ipparco erano interamente contenute, ciascuna nel rettangolo sferico esteso 30º in eclittica precedentemente definito, col trascorrere del tempo ne sono un po’ alla volta uscite, sicchè oggi, dopo circa 2100 anni dalla scoperta di Ipparco, essendo avvenuta una retrogradazione di circa 25º, tutte le caselle sferiche ampie 30º sono egualmente slittate in senso retrogrado, per cui, oggi, nella casella di 30º che parte dal punto ^ è collocata quasi completamente la costellazione dei Pesci, successivamente, nella casella successiva la costellazione dell’Ariete, e così via.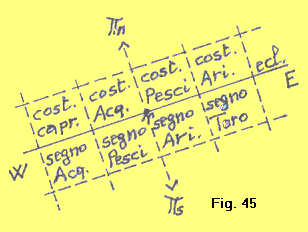

Oggi, dunque, all’inizio della primavera, si dovrebbe dire che il Sole entra nella costellazione dell’Ariete. Ma, per rispettare le indicazioni tradizionali, si preferisce conservare i nomi zodiacali a partire dall’equinozio di primavera come erano ai tempi di Ipparco, avvertendo che essi devono essere ora intesi come segni dello zodiaco (come caselle sferiche di 30º, non come costellazioni.). Cioè oggi si dice che all’epoca dell’equinozio di primavera il Sole entra nel segno di Ariete (nel quale, ripetiamo, si trova ormai la costellazione dei Pesci).



ANNO TROPICO E ANNO SIDEREO
Altra conseguenza della precessione degli equinozi è che l’intervallo di tempo impiegato dal Sole per transitare due volte consecutive per il punto ^, intervallo detto, come sappiamo, anno tropico, è minore dell’intervallo che il Sole impiega per fare un giro completo di sfera celeste, intervallo detto anno sidereo (il punto ^ “va incontro” al Sole di 50”.25 ogni anno). La durata dell’anno tropico, come sappiamo, è di 365.2422 giorni solari medi, cioè 366.2422 giorni siderei (in un anno tropico il punto ^ fa esattamente un giro di sfera celeste in più del Sole).



PARALLASSE ORIZZONTALE E ANNUA
Con il termine parallasse si intende l'apparente cambiamento di posizione che subisce uno stesso oggetto quando viene osservato da due diversi punti di vista. Il modo più elementare di illustrare il concetto di parallasse è quello di protendere un braccio verso l'avanti e, chiudendo alternativamente l'occhio destro e il sinistro, osservare come un dito della mano venga visto proiettato su due differenti punti lontani.

Incominciamo col dare il concetto di parallasse orizzontale. Supponiamo che un osservatore O, situato sulla superficie terrestre, abbia un astro qualsiasi, ad esempio la Luna L all'orizzonte. Evidentemente per lui l'altezza della Luna è zero. Un ipotetico osservatore, situato invece al centro della Terra T, la osserva invece elevata sull'orizzonte dell'angolo OLT = p, che è appunto la parallasse orizzontale lunare.

Adesso diamo il concetto di Parallasse annua di una stella A. E' l'angolo p sotto il quale dalla stella A si vedrebbe il semiasse maggiore dell'orbita terrestre ST, supposto normale alla congiungente stella-Sole. Per definizione, dal triangolo AST, rettangolo in S, si ha: sen(p) = ST/AT.
Se si considera come unità di misura delle distanze astronomiche la distanza media Terra-Sole (la cosiddetta Astronomic Unit, AU), se cioè si pone ST = 1 e si esprime AT = d in AU, risulta: sen(p) = 1/d.

Essendo p un angolo molto piccolo (inferiore a 1" per qualsiasi stella), possiamo ammettere questa approssimazione (usata spesso in trigonometria per gli angoli piccoli): sen(p) = p"•sen(1"), per cui possiamo scrivere: p"•sen 1" = 1 / d da cui p" = (1/d)•(1/sen(1")), e, siccome la quantità 1/sen 1" vale 206265, si ha: p" = 206265•(1/d)

Questa relazione mostra che col crescere della distanza di una stella dalla Terra, la sua parallasse annua diminuisce. La stella più vicina alla Terra, quella cioè di maggior parallasse annua, è la Proxima Centauri, la cui parallasse annua è di circa 3/4 di secondo di arco, e corrisponde a una distanza di circa 4 anni-luce.

L'effetto di parallasse, causato dallo spostamento dell'osservatore sull'orbita terrestre tra i punti H e K, si traduce in uno spostamento periodico della stella sulla sfera celeste. In genere, cioè, mentre la Terra percorre tutta la sua orbita, le visuali Terra-stella incontrano la sfera celeste in punti differenti che, se congiunti, darebbero luogo a un'ellisse, detta ellisse parallattica, K'-H'. La determinazione della parallasse è uno dei problemi più difficili dell'astronomia siderale. Conosciuta la parallasse p, la distanza d della stella si ricava da : d = 206265 / p". La prima stella di cui fu trovata la parallasse fu la 61 Cygni e la determinazione fu eseguita da F. W. Bessel (1784 - 1846) nel 1838.



ABERRAZIONE DELLA LUCE
La luce non si propaga istantaneamente ma con una velocità di circa 300.000 Km/sec. Questa velocità, componendosi con quella della Terra lungo la sua orbita, genera una deviazione dei raggi luminosi provenienti dalle stelle, deviazione che prende il nome di aberrazione. Per spiegare questo fenomeno, si supponga di osservare la caduta della pioggia, senza vento, dall'interno di un'automobile. Se l'auto è ferma, le gocce d'acqua saranno viste scendere verticalmente. Se invece la macchina si mette in moto, le gocce d'acqua appariranno, dall'interno dell'auto, cadere non più lungo la verticale ma inclinate (e ciò in assenza di vento esterno). Lo stesso vento prodotto dal moto dell'automobile non ha alcuna influenza sul fenomeno che dipende unicamente dalla composizione della velocità verticale di caduta delle gocce con la velocità orizzontale dell'automobile.

Volendo spiegare il fenomeno dell'aberrazione, sia S il Sole e sia TK la direzione istantanea del movimento della Terra lungo la sua orbita. Tale direzione istantanea determina sulla sfera celeste un punto verso cui si dirige in quell'istante la Terra. Questo punto è detto apice del movimento annuo terrestre. La posizione istantanea dell'apice si muove sull'eclittica in senso diretto, mantenendosi sempre a circa 90º di differenza di longitudine dal Sole.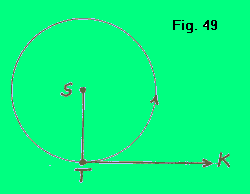

Allora, nella figura 50, supponendo che ST sia la direzione di provenienza di un raggio luminoso da una stella S, e che TK sia una direzione istantanea dell'apice, prendiamo su ST un segmento TA rappresentativo della velocità della luce, su TK un segmento TB rappresentativo (ovviamente in scala) della velocità della Terra lungo la sua orbita (circa 30 Km/sec). Costruito il parallelogrammo TACB, la diagonale CT sarà rappresentativa della direzione e della velocità di provenienza del raggio di luce. La stella è vista in S' anzichè in S, e il suo raggio di luce ha subito la deviazione STS' = w che è appunto l'aberrazione. Il suo valore è evidentemente molto piccolo, ma di essa devono tenere conto gli astronomi.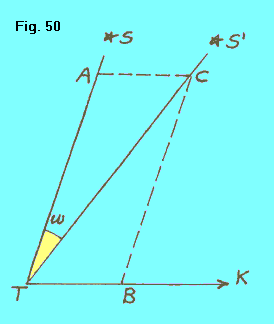



SISTEMI DI COORDINATE CELESTI
Come si hanno le coordinate geografiche terrestri (latitudine e longitudine), identificanti un punto della superficie terrestre, così in astronomia esistono sistemi di coordinate celesti, evidentemente finalizzate all’identificazione di punti della "superficie sferica" celeste.
Un sistema di coordinate astronomiche, per poter essere definito richiede che vengano dati per esso alcuni riferimenti. Questi sono:
  • un polo del sistema
  • un cerchio base per la coordinata verso nord e verso sud
  • un semicerchio origine per la coordinata verso est e verso ovest.
Si dice che un sistema di coordinate celesti è uranografico quando adotta quali cerchi e semicerchi di riferimento elementi immobili rispetto alle stelle fisse. Così facendo, in questo tipo di sistema, la posizione di un astro viene data indipendentemente dalla posizione dell’osservatore sulla Terra. Daremo la descrizione di due sistemi uranografici: (1) il sistema equatoriale e (2) il sistema eclittico.
Si dice invece che un sistema di coordinate è locale quando i cerchi di riferimento sono tali da far sì che le coordinate dell’astro fornite dipendano dalla posizione dell’osservatore. Daremo in seguito la descrizione di due sistemi locali: (1) il sistema orario e (2) il sistema altazimutale. (Osservando una sfera celeste, il lettore è in grado di distinguere se si tratta di una sfera uranografica o locale dal fatto che nelle sfera locale è sempre presente lo zenit (rappresentativo sulla sfera celeste dell’osservatore) che invece nella sfera uranografica manca).



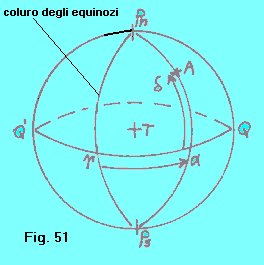
SISTEMA URANOGRAFICO EQUATORIALE
E’ basato su questi elementi di riferimento:
  • come polo fondamentale il polo celeste nord
  • come cerchio fondamentale l’equatore
  • come semicerchio origine il meridiano passante per il punto ^, detto coluro degli equinozi
In questo sistema le coordinate di un astro qualsiasi A, sono espresse da:
  • la declinazione (d, delta), arco di meridiano, contato da 0º a 90º, verso nord o verso sud, a partire dall’equatore celeste.
  • l’ascensione retta (a, alfa), arco di equatore, contato da 0º a 360º, a partire dal punto ^, sempre in senso diretto.



SISTEMA URANOGRAFICO ECLITTICO
In questo sistema si assumono per riferimento i seguenti elementi:
  • come polo di riferimento il polo celeste nord dell’eclittica
  • come cerchio base l ‘ eclittica
  • come semicerchio origine il meridiano d’eclittica passante per il punto ^
Le coordinate di un astro qualsiasi A, sono:
  • latitudine celeste, arco di meridiano d’eclittica contato da 0º a 90º, verso nord o verso sud.
  • longitudine celeste, arco di eclittica contato a partire dal punto ^, da 0º a 360º, sempre nel verso diretto, fino al piede del meridiano d’eclittica passante per l’astro.



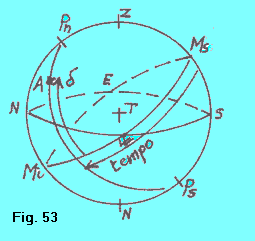
SISTEMA LOCALE ORARIO
I riferimenti di questo sistema sono:
  • come polo di riferimento, il polo elevato (attenzione! Non sempre il polo nord)
  • come cerchio base l ‘ equatore
  • come semicerchio origine il meridiano superiore (quello che contiene lo zenit).
Le coordinate di un astro qualsiasi sono:
  • la declinazione, arco di meridiano compreso tra equatore e astro, contato da 0º a 90º, verso l’astro.
  • l ‘ angolo orario (tempo), arco di equatore, contato sempre a partire dal mezzo cielo superiore fino al piede del meridiano passante per l’astro, sempre nel senso Ms-W-Mi-E, da 0º a 360º



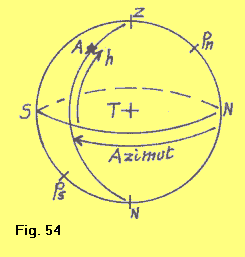
SISTEMA LOCALE ALTAZIMUTALE
I riferimenti sono:
  • quale polo lo zenit
  • quale cerchio base l’orizzonte celeste
  • quale semicerchio origine il verticale nord.
Le coordinate sono:
  • l ‘ altezza, arco di verticale compreso tra orizzonte e astro, contato da 0º a 90º a partire dall’orizzonte.
  • l ‘ azimut, arco di orizzonte, contato sempre a partire dal punto cardinale nord, fino al piede del verticale passante per l’astro, da 0º a 360º.



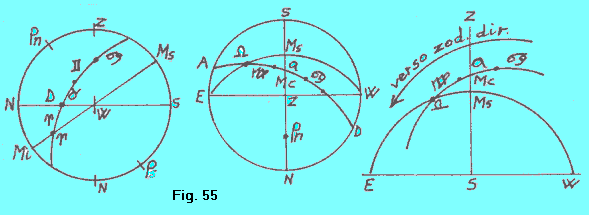
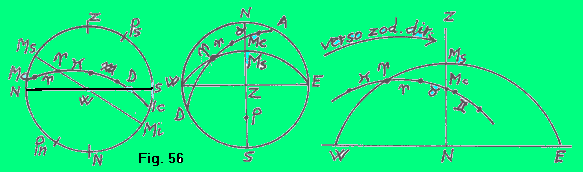
L’ECLITTICA ALLE LATITUDINI SUD
E’ opportuno che il lettore fissi la sua attenzione sul cambiamento che il senso zodiacale diretto subisce nell’emisfero terrestre sud. Precisiamo anzitutto che la figura di destra di ciascuno dei due gruppi di tre figure che seguono dà una rappresentazione, sia pure grossolana, della situazione celeste quale si avrebbe (1) nella figura 55, per un osservatore che, situato nell’emisfero nord, volga lo sguardo verso sud e (2) nella figura 56, per un osservatore che, nell’emisfero sud, volga lo sguardo verso nord.
Dalle tre immagini di figura 55 si ha dunque la rappresentazione dell’eclittica per l’emisfero nord. Da tutte e tre (ma specialmente da quella di destra) si vede che un osservatore nell’emisfero nord, volgendosi verso l’eclittica, cioè verso sud, vede il verso zodiacale diretto (cioè il verso in cui si susseguono le costellazioni Ariete, Toro, Gemelli, ecc.) svilupparsi in senso antiorario (come avevano a suo tempo indicato).

Dalle tre immagini di figura 56 invece, la rappresentazione dell’eclittica sulla sfera celeste per l’emisfero sud. Da esse si vede (in particolare da quella di destra) che un osservatore nell’emisfero sud, che si volga verso l’eclittica, cioè verso nord, vede il verso zodiacale diretto (cioè il verso della successione di costellazioni Ariete, Toro, Gemelli, ecc.,) svilupparsi in senso orario.



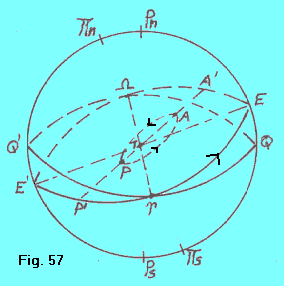
EQUINOZI, SOLSTIZI, APSIDI
Prendiamo in esame ancora una sfera celeste uranografica geocentrica (si immagina che sia il Sole a percorrere l’ellisse e quindi lo si vede, dal centro, proiettato sull’eclittica). La linea ^-T-W , detta linea degli equinozi. , è soggetta al movimento di retrogradazione dei nodi (50”.25 all’anno). La linea EE’, detta linea dei solstizi, congiunge i punti di massima declinazione nord-sud raggiunti dal Sole. La linea A’-A-P-P’, detta linea degli apsidi, congiunge i punti di minima e massima distanza del Sole dalla Terra, P e A. La linea degli apsidi ruota di circa 12” all’anno nel verso diretto. Questo movimento è detto progressione del perigeo. Nell’anno 1250 circa le linee degli apsidi e dei solstizi coincidevano.



ZONE DELLA SUPERFICIE TERRESTRE
In questa figura la Terra, al centro, è posta (grossolanamente) in relazione con la sfera celeste. Così come il piano passante per l’equatore terrestre q-q’ interseca la superficie della sfera celeste secondo l’equatore celeste Q-Q’, allo stesso modo:
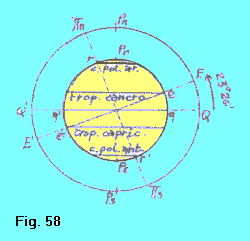  • Il piano passante per l’eclittica E-E’ interseca la superficie terrestre secondo il cerchio massimo e-e’. I due paralleli terrestri condotti per i punti di massima latitudine nord-sud di questo cerchio massimo, sono detti tropico del cancro e tropico del capricorno (latitudine 23º26’ N/S)
  • Il piano perpendicolare all’eclittica e contenente i poli della stessa pn-ps, nonché i punti ^ e W, interseca anch’esso la superficie terrestre secondo il cerchio massimo r-r’. I due paralleli terrestri condotti per i punti di massima latitudine nord/sud di questo secondo cerchio massimo sono detti circolo polare artico e circolo polare antartico.

La Terra risulta così suddivisa in cinque zone:
  • una zona detta torrida, compresa tra i tropici e l’equatore
  • due zone dette temperate, comprese tra tropico e circolo polare (N/S)
  • due zone dette calotte glaciali





Esercitazioni    (3)

(I posizionamenti di astri che seguono devono essere eseguiti facendo in modo che gli astri appaiano nella metà di sfera celeste "da questa parte del foglio").

  1. Su una sfera locale posizionare gli astri A e B con le seguenti coordinate altazimutali:
    1. Astro A: azimut 55º, altezza 30º - Osservatore in latitudine 40º N
    2. Astro B: azimut 130º, altezza 50º - Osservatore in latitudine 40º S
    3. Astro A': azimut 220º, altezza 55º - Osservatore in latitudine 40º N
    4. Astro B': azimut 300º, altezza 10º - Osservatore in latitudine 40º S
  2. Su una sfera locale posizionare gli astri C e D con le seguenti coordinate orarie:
    1. Astro C: angolo orario 230º, declinazione 55º N - Osservatore in latitudine 45º N
    2. Astro D: angolo orario 330º, declinazione 15º S - Osservatore in latitudine 15º S
  3. Tracciare la sfera locale (in proiezione ortografica per semplicità) per la latitudine 50º N. Quindi tracciare su di essa l'eclittica, posizionandola per i seguenti istanti della giornata siderale:
    1. istante ts = 3h 30m (52º 30')
    2. istante ts = 20h (300º)
    (Anche per questi posizionamenti dell'eclittica, fare in modo che il punto ^ càpiti "da questa parte del foglio").





PUNTI DI VISTA ELIOCENTRICO E GEOCENTRICO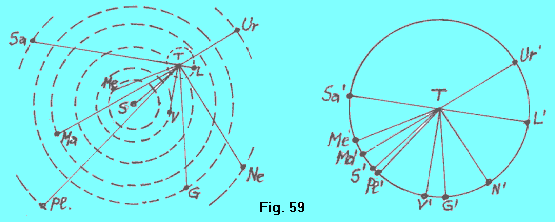

Nella figura 59, a sinistra si ha una situazione eliocentrica relativa ad un certo istante. A destra si ha la corrispondente situazione geocentrica, per lo stesso istante. I punti L’, Me’, V’, Ma’, G’, ecc., indicativi rispettivamente delle posizioni di Luna, Mercurio, Venere, Marte, Giove, ecc., sono ottenuti portando sul cerchio di destra, rappresentativo della sfera celeste geocentrica, successivamente i raggi:
- TL’ parallelo a TL
- Tme’ parallelo a Tme
- TV’ parallelo a TV
- Tma’ parallelo a Tma
- TG’ paralle lo a TG, ecc.

Il lettore tenga poi presente che, mentre il terzo cerchio tratteggiato a partire dal centro della figura di sinistra, rappresentando l’orbita della Terra, deve intendersi giacente nel piano del foglio, gli altri cerchi devono essere immaginati posti su piani che formano con il detto piano angoli variabili da circa 1º a circa 7º (con l’eccezione di Plutone). Si tratta, come già accennato dei valori di obliquità delle orbite planetarie che fanno si che i pianeti appaiano muoversi non certamente sull’eclittica ma nell’ambito della fascia zodiacale, che si estende appunto circa 8º a nord e a sud dell’eclittica.



I MOTI DEI PIANETI
Mentre le cosiddette stelle fisse conservano le loro posizioni reciproche praticamente per un tempo indefinito, i pianeti ci appaiono dotati di moti strani. Ciò è dovuto alle seguenti cause:
  • Come la Terra, anche i pianeti compiono la loro rivoluzione attorno al Sole e quindi la visuale Terra-pianeta, continuamente variabile nello spazio, va a proiettarsi in punti sempre diversi della sfera celeste
  • Le orbite dei pianeti (come già detto nel paragrafo precedente) sono poco inclinate rispetto al piano dell’orbita terrestre (entro gli 8º circa, solo l’orbita di Plutone ha un’inclinazione anomala di circa 17º, figura 60 a). Queste due ragioni fanno sì che quei moti strani avvengano nella fascia zodiacale, appunto 8º circa a nord e a sud dell’eclittica (tranne Plutone, come detto).

Mercurio e Venere sono detti pianeti interni o inferiori perchè la loro orbita è interna rispetto a quella della Terra. Tutti gli altri sono detti esterni o superiori (in ordine di distanza dalla Terra: Marte, Giove, Saturno, Urano, Nettuno e Plutone). Per capire come ci appare il moto di un pianeta interno rispetto al Sole, dobbiamo tenere presente che come noi “vediamo” il Sole muoversi apparentemente tra le stelle, così anche i pianeti interni vengono trascinati con lui, sempre mantenendo ciascuno il proprio moto attorno a lui. Questo fa sì che noi vediamo i pianeti interni discostarsi relativamente poco dal Sole. Per un pianeta interno si parla quindi di massima elongazione est e ovest (V1, V2, figura 60 b). Precisamente, per Venere l’elongazione arriva a circa 46º, mentre per Mercurio arriva al massimo a 25º circa. Per un pianeta esterno, invece, l’elongazione dal Sole può assumere tutti i valori, da 0º a 360º perché, essendo esterno, può essere visto da noi per tutta l’ampiezza della sfera celeste, indipendentemente dal Sole.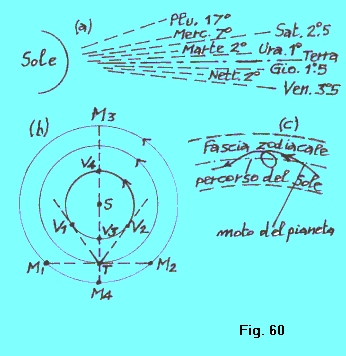

In particolare quindi, quando l’elongazione è 90º si dice che il pianeta è in quadratura (posizioni M1, quadratura orientale, o M2, quadratura occidentale, della figura 60 b). Quando l’elongazione è 180º sidice che il pianeta è in opposizione (posizione M4), mentre quando l’elongazione è 0º si dice che il pianeta è in congiunzione (posizione M3). Per un pianeta interno, invece, quando esso si trova in V3 (con la Terra in T) si dice che esso è alla congiunzione inferiore, mentre quando è in V4 si dice che è alla congiunzione superiore.

Studiamo il moto di un pianeta interno, ad esempio Venere, così come ci appare dalla Terra. Nella figura 61 le orbite della Terra e di Venere sono immaginate circolari, per semplificare, e viste dal polo nord dell'eclittica con situazione eliocentrica. Essendo l'orbita terrestre suddivisa in 6 parti eguali, immaginiamo (semplificando) che ogni arco di 60º sia percorso in 365.25 : 6 = 60.87 giorni. Siccome Venere ha un periodo tropico di 224.7 giorni, in 60.87 giorni immaginiamo (anche qui semplificando) che percorra un arco di orbita risultante da 224.7 : 360º = Xº : 60.87, da cui X = 97º.5. Allora, mentre la Terra percorre gli archi AB, BC, CD, ecc., ampi ciascuno 60º, Venere percorrerà gli archi ab, bc, cd, ecc., ampi ciascuno 97º.5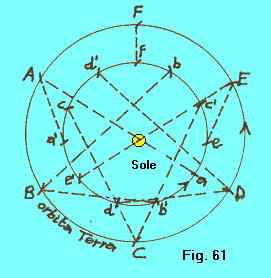

Nella figura 62 si immagina di vedere l'orbita risultante di Venere, sempre dal polo nord dell'eclittica, ma con situazione geocentrica. I punti della curva epicicloide descritta da Venere, a, b, c, d, e, f, a', b', c', d', e', sono ottenuti portando i segmenti Ta, Tb, Tc, . . . . Te', paralleli ed uguali rispettivamente ai segmenti Aa, Bb, Cc, . . . . Ae' della figura 61. Vediamo che il piccolo loop della figura 62 viene descritto ogni volta da Venere nella fase in cui, mentre la Terra percorre l'arco EFA, Venere percorre contemporaneamente l'arco efa', cioè ogni volta che dalla Terra Venere è in fase di congiunzione inferiore. Durante quella fase si hanno i stazionamenti e la breve fase di moto retrogrado (Venere nell'intorno del punto f).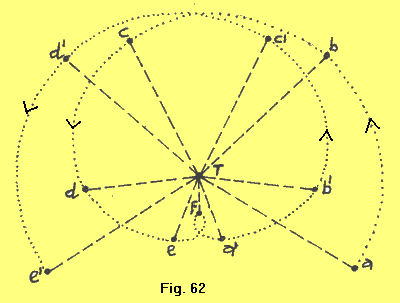


Studiamo ora il moto di un pianeta esterno, ad esempio Marte. Con lo stesso ragionamento fatto per Venere, poichè Marte ha un periodo tropico di 687 giorni, l'arco di orbita di Marte percorso in 60.87 giorni risulterà da: 360º : 687 = X : 60.87, da cui X = 31º.9. La figura 56 ci mostra dunque che mentre la Terra percorre gli archi AB, BC, CD, ecc., Marte percorrerà simultaneamente gli archi ab, bc, cd, ecc.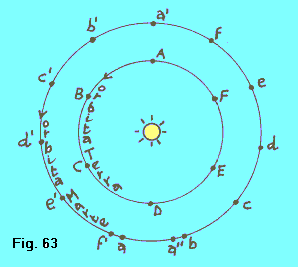

Similmente al modo con cui dalla figura 62 avevamo ottenuto l'epicicloide di Venere, dalla figura 64 otterremo i punti dell'epicicloide di Marte a, b, c, d, e, f, a', b', c', d', e', f', a" portando da T i segmenti Ta, Tb, Tc, . . . Ta" uguali e paralleli rispettivamente ai segmenti Aa, Bb, Cc, . . . Aa" della figura 63. Il piccolo loop della figura 64 viene descritto ogni volta da Marte, mentre la Terra percorre l'arco FAB, Marte percorre contemporaneamente l'arco fa'b', cioè ogni volta che dalla Terra Marte è in fase di opposizione. Durante quella fase si hanno i stazionamenti (negli intorni dei punti f e b'), nonchè la fase di moto retrogrado, (nell'intorno del punto a').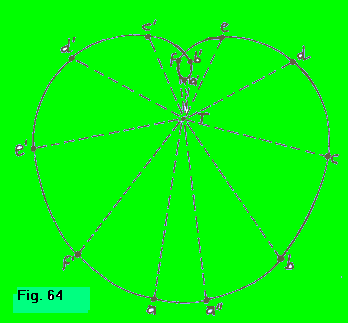
Concludiamo dicendo che mentre i pianeti interni si discostano poco dal Sole, quelli esterni possono assumere qualunque scostamento (si dice “elongazione”) dal Sole. Osserviamo però che anche i pianeti interni possono assumere tutte le longitudini da 0º a 360º (siccome il Sole ha un moto apparente di 360º, anche i pianeti interni, sempre poco scostati dal Sole, possono assumere qualunque longitudine.

Infine, diamo ragione delle qualifiche di vespertina e di mattutina, attribuite a Venere. Quando Venere è a est del Sole (V1 in figura 60 b), tramontando dopo il Sole, diviene visibile dopo il tramonto di esso, e quindi viene detta vespertina (figura 65).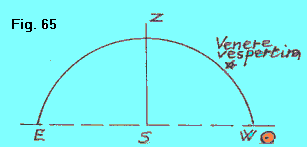

Quando invece si trova a ovest del Sole (V2 in figura 60 b), sorgendo prima del Sole, è visibile appunto solo prima del sorgere del Sole e quindi è detta mattutina (figura 66).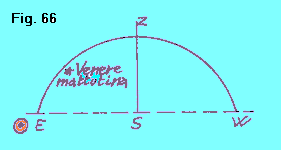



RIVOLUZIONI TROPICHE E SINODICHE
Rivoluzione tropica (o anche siderale) di un pianeta è l'intervallo di tempo che intercorre tra due congiunzioni successive del pianeta con una stessa stella fissa. Per rivoluzione sinodica, invece, si intende l'intervallo che intercorre tra due successive opposizioni. In figura 64, nel caso di Marte, è l'intervallo di tempo che intercorre tra due successivi passaggi di Marte per il punto f', che, ovviamente, non è fisso nello spazio ma si sposta in senso retrogrado. Nella tabella accanto, diamo i valori dei due periodi per alcuni pianeti. (Il lettore tenga presente che mentre la rivoluzione tropica di ogni pianeta è indipendente dalla rivoluzione terrestre e quindi è costante, la sinodica risulta, per ogni pianeta, dalla combinazione della tropica con la terrestre, e quindi ogni rivoluzione tropica avrà una durata dipendente dalle velocità dei due pianeti, per cui quei valori di rivoluzione sinodica si intendono medi).
Rivol. tropicaRivol. sinodica
Mercurio87d.9115d.9
Venere224d.7583d.9
Marte687d779d.9
Giove11a.862398d.9
Saturno29a.567378d.1



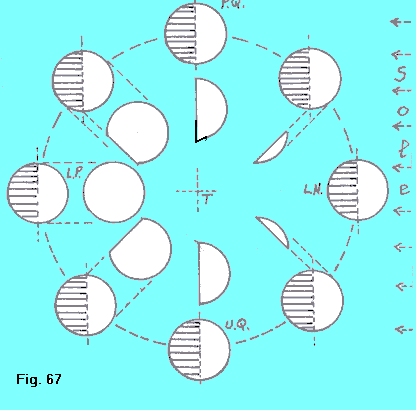
LE FASI LUNARI
Il fenomeno delle fasi lunari è strettamente collegato alle elongazioni che la Luna assume rispetto al Sole, durante il suo mese lunare. Durante esso si svolge l’intero ciclo delle fasi lunari, cioè tutti gli aspetti luminosi del disco lunare. Partendo dalla congiunzione, il disco lunare rivolto verso l’osservatore è totalmente oscuro. E’ durante questa fase che possono aver luogo le eclissi di Sole (corpo lunare che impedisce parzialmente o totalmente, la visione del Sole). Questa fase si dice Luna nuova e durante essa la Luna sorge, passa al meridiano e tramonta assieme al Sole.Dopo circa tre giorni e mezzo la Luna avrà assunto un angolo di elongazione di circa 45º a levante del Sole (il moto di rivoluzione della Luna si compie in senso diretto, come quello del Sole, ma con velocità circa 13 volte maggiore).

In questa fase, dalla Terra il disco lunare apparirà illuminato per circa la quarta parte. Si dice allora che la Luna è al primo ottante. In questa fase la Luna ritarderà di circa 3 ore il sorgere, il passaggio al meridiano e il tramonto rispetto al Sole. E durante questa fase la parte convessa della falce lunare è rivolta verso ponente.
Dopo circa 7 giorni e mezzo dalla Luna nuova, cioè quando l’elongazione è 90º, mezzo disco lunare appare illuminato. Si dice che la Luna è al primo quarto. La Luna sorge circa a mezzodì, passa al meridiano al tramonto del Sole, e tramonta circa a mezzanotte.
Dopo circa 14 giorni e mezzo dalla Luna nuova, cioè quando l’elongazione è 180º, si dice che la Luna è in opposizione. Questa fase è detta Luna piena: è visibile l’intero disco lunare. La Luna sorge quando il Sole tramonta, e viceversa. Durante questa fase possono aver luogo le eclissi di Luna (la visione della Luna è impedita dal fatto che la Luna va ad immergersi nel cono d’ombra terrestre).
Dopo circa 22 giorni dal novilunio, cioè quando l’angolo di elongazione è 270º, mezzo disco lunare apparirà illuminato, ma, questa volta, la parte che è rivolta a levante rispetto al Sole (ora la parte convessa della falce lunare è rivolta verso levante). Questa fase si dice ultimo quarto: la Luna sorge circa a mezzanotte, passa al meridiano all’alba e tramonta circa a mezzodì. Finalmente, dopo circa 29 giorni e mezzo dalla Luna nuova, la Luna torna in congiunzione con il Sole e le fasi descritte sopra ricominciano. Un’ultima osservazione riguardante il moto della Luna: siccome il periodo della rivoluzione lunare attorno alla Terra è uguale al periodo di rotazione attorno al proprio asse (entrambi i movimenti hanno senso diretto), la Luna volge verso la Terra sempre lo stesso emisfero.


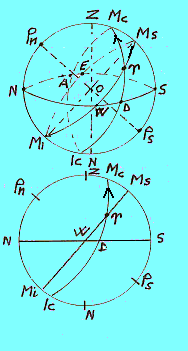
Esercitazioni    (4)

Su sfere celesti locali, tutte per la latitudine 40º N, posizionare l'eclittica per i seguenti istanti della giornata siderale:
(1) ts = 38º, (2) ts = 122º, (3) ts = 244º, (4) ts = 296º.
Come al solito, eseguire il tracciamento della sfera celeste in modo che il punto ^ appaia nella semisfera celeste "da questa parte del foglio".
Sull'eclittica indicare con una freccetta il verso zodiacale diretto. Tracciare le sfere celesti sia in modo prospettico che abbreviato.


Diamo la soluzione per il caso (1).
Siccome gli angoli orari si contano nel senso Ms-W-Mi-E, dovendo tracciare un arco di 38º dal Ms fino al punto ^, per fare in modo che il punto ^ appaia "da questa parte del foglio", si deve tracciare la sfera celeste con l'asse Pn-Ps inclinato come in figura (Pn in alto a sinistra e Ps in basso a destra). Alla fine, per tracciare l'eclittica, segnato sull'equatore il punto ^, a 38º dal Ms, si fa passare per questo punto l'eclittica, inclinata di circa 23º 26' rispetto all'equatore, verso il polo nord, Pn. La freccia del verso zodiacale diretto si segna in modo che l'osservatore O, al centro, volgendosi verso l'eclittica, "veda" il verso svilupparsi in senso antiorario.





IL CALENDARIO GREGORIANO
Il lettore troverà notizie sui sistemi cronologici dell'antichità, fino al calendario giuliano, nella sezione storica. Qui accenniamo brevemente all'ultima riforma del calendario, che venne promulgata da Papa Gregorio XIII (ma che fu attuata subito soltanto dai paesi cattolici). La riforma consistette (1) nel sopprimere 10 giorni, passando da giovedì 4 ottobre 1582 a venerdì 15 ottobre, (2) mantenendo inalterata l’introduzione degli anni bisestili secondo la regola a suo tempo data con il calendario giuliano (bisestili gli anni divisibili per 4), vennero considerati comuni (non bisestili) gli anni secolari, tranne quelli divisibili per 400. Quindi non furono bisestili gli anni 1700, 1800, 1900, mentre lo è stato il 2000.

NOTA - Il lettore che desideri rendersi conto del perché nel corso dei secoli si siano avute le varie riforme del calendario, tenga presente che ciò dipende dal fatto che il cosiddetto anno tropico (cioè l’intervallo che intercorre tra due successivi ritorni del Sole al punto ^) non contiene un numero intero di giorni solari e nemmeno una frazione intera, ma ne contiene 365.2422 (in parole più semplici, in un anno tropico il Sole non compie un numero intero di giri apparenti intorno alla Terra ma ne compie un po’ meno di 365 e un quarto). Siccome le date civili sono evidentemente sempre computate contando giorni interi, con il passare dei secoli (malgrado il giorno bisestile introdotto con la riforma giuliana) la differenza tra 365.25 (365 e un quarto) e 365.2422 si è accumulata in circa 10 giorni di differenza tra l’istante astronomico di inizio della primavera 1582 e la data civile dell’evento secondo il calendario giuliano. Quindi, uno dei punti della riforma gregoriana fu la soppressione di quei dieci giorni. Osserviamo a questo proposito che la riforma gregoriana non è ancora perfetta. Rimane sempre una piccola differenza che in 33 secoli (a partire dal 1582) si accumulerà in un giorno.



LA DATA DELLA PASQUA
Durante il Concilio ecumenico di Nicea, presieduto dall’imperatore Costantino, nel 325 d.C., si stabilì che la Pasqua cadesse la prima domenica seguente il plenilunio immediatamente successivo all’equinozio di primavera.. Allora, nel caso di un plenilunio che abbia luogo il 21 marzo e che tale giorno sia un sabato, la Pasqua cadrà il 22 marzo, e si dice bassa. Nel caso di un plenilunio che invece abbia luogo il 20 marzo, il successivo non potrà aversi prima del 18 aprile. Allora, se questa data capita di domenica, la Pasqua si celebrerà la domenica successiva, cioè il 25 aprile, e verrà perciò detta alta.
Nota la data della Pasqua, possono essere stabilite le date delle feste mobili ad essa legate, e cioè la Settuagesima, le Ceneri, l’Ascensione, la Pentecoste, il Corpus Domini e la Prima Domenica di Avvento



IL GIORNO GIULIANO
Per la determinazione della data, nei calcoli astronomici si usa spesso il giorno giuliano, che è una delle modalità astronomiche usate per indicare un istante temporale. Precisamente, il numero indicativo del giorno giuliano relativo a un certo istante t, è il numero di giorni (ed eventuali frazioni di giorno) trascorsi dall'istante mezzodì di Greenwich del 1º gennaio dell'anno 4713 a.C. fino all'istante t (il francese J. Scaliger, introducendo nel 1583 questo modo di computare un istante astronomico, scelse una data così lontana in modo da far sì che praticamente tutti gli eventi storici conosciuti risultassero in un ambito tale da non fornire mai per essi un numero negativo di giorno giuliano).
L'istante del mezzodì di Greenwich del 1 gennaio 4713 a.C. si indica astronomicamente con la notazione -4712, 1, 1.5.
Infatti, è noto che l'Era cristiana ha inizio con l'anno 1 a.D. (anno Domini), che l'anno precedente (nel mese di dicembre del quale si ritiene sia nato Gesù Cristo) è chiamato anno 1 a.C., che l'anno ancora precedente è indicato con 2 a.C., ecc. In modalità astronomica l'anno 1 a.C. è indicato con anno 0 e gli anni precedenti sono indicati con numeri negativi. Si veda la tabella accanto.
Modalità a.C / d.C. Modalità astronomica
20002000
....................
11
1 a.C.0
2 a.C.-1
3 a.C.-2
....................
4713 a.C.-4712

Si osservi ora quest'altra tabella:
Data civile Data astronomica Giorno giuliano
00h 00m GMT   1.1.4713 a.C.-4712, 1, 1.0-0.5
12h 00m GMT   1.1.4713 a.C.-4712, 1, 1.50
00h 00m GMT   2.1.4713 a.C.-4712, 1, 2.00.5
15h 07m GMT   28.5.585 a.C.-584, 5, 28.631507900.13
12h 00m GMT   27.1.333 d.C.333, 1, 27.51842713.0
00h 00m GMT   15.2.19951995, 2, 152449763.5
12h 00m GMT   15.2.19951995, 2, 15.52449764.0
00h 00m GMT   16.2.19951995, 2, 162449764.5
Come si vede, nell'indicazione del giorno, tra data astronomica e giorno giuliano c'è la differenza di 0.5 giorni. Questo è dovuto al fatto che mentre la data civile scatta, come è noto, alla mezzanotte, il giorno giuliano scatta al mezzodì.
Osserviamo anche che su certi testi astronomici, per indicare la data astronomica 1899 Dicembre 31.5 (cioè le 12h del 31.12.1899), si usa la notazione 1900 Gennaio 0.5 (cioè si fa uso anche della cifra 0 per indicare il giorno).



CALCOLO DEL GIORNO GIULIANO
Riteniamo opportuno includere in queste note anche un algoritmo per il calcolo del giorno giuliano per quei lettori interessati a calcoli astronomici in genere.
Precisamente descriviamo l'algoritmo che abbiamo tratto dal libro Astronomical Algorithms, di Jean Meeus, che ci sembra il più compatto.
Affinchè questo algoritmo possa essere applicato sia ad anni positivi che negativi, è necessario che in esso venga fatto uso della funzione I(x). Questa funzione è simile alla funzione del linguaggio Pascal Trunc(x). Restituisce la parte di numero reale x, che precede il punto decimale. Quindi I(5.02) restituisce 5, mentre I(-7.83) restituisce -7 (tenere presente che invece la funzione BASIC Int(x) ha un comportamento diverso: mentre Int(5.02) restituisce 5, Int(-7.83) restituisce 8).
Allora, per definire la funzione I(x) nel lingiaggio BASIC si può ricorrere, oltre che alla Int, ad altre due funzioni BASIC predefinite:
  • SGN(x), che restituisce 0 se x = 0, 1 se x > 0, -1 se x < 0
  • ABS(x), che restituisce x se x >= 0, -x se x < 0


Ecco dunque l'algoritmo:
  • Sia Y il numero dell'anno (positivo, negativo o zero), M quello del mese (1 - 12) e D quello del giorno (1 - 31, con eventuali decimali)
  • Se M > 2 lasciare Y e M immutati, altrimenti porre Y = Y -1 e M = M+12
  • Se la data in ingresso è successiva o uguale al 15.10.1582, porre A = I(Y/100) e B = 2 - A - I(A/4), altrimenti porre A = B = 0
  • Il giorno giuliano JD è dato da:
        JD = I(365.25•(Y + 4716)) + I•(30.6001•(M+1)) + D + B - 1524.5

    Ed ecco una routine BASIC che realizza l'algoritmo: 
    
100     '       JDMEEUS.BAS - Giorno giuliano con algoritmo di Meeus
110     DEFDBL  A-Z                ' necessita doppia precisione
120     DEF FNI(X) = SGN(X) * INT(ABS(X))       ' funzione I(x)
130     CLS                                     ' pulisce schermo
140     INPUT"Giorno, mese, anno  (gg,mm,aaaa):   ", D,M,Y
150     '   Trasforma input in data modularizzata Y.MMGGdecimali
160     IF Y<0 THEN DATAST=Y-M/100-D/10000 ELSE DATAST= Y+M/100  
        +D/10000
170     IF M=1 OR M=2 THEN Y=Y-1 : M=M+12
180     IF DATAST >= 1582.1015# THEN A=FNI(Y/100) : B=2-A+FNI(A/4)
190     JD = FNI(365.25#*(Y+4716)) + FNI(30.6001#*(M+1))+D+B-1524.5
200     PRINT "Giorno giuliano :    "; JD
210	  END



DATA CIVILE IN FUNZIONE DEL GIORNO GIULIANO
Dallo stesso libro di Jean Meeus traiamo anche l'algoritmo per il calcolo inverso: a partire da un giorno giuliano, calcolare la corrispondente data. Anche qui viene fatto uso della funzione I(x), sopra definita. Il numero del giorno della data calcolata dall'algoritmo può avere una parte decimale. Questo è l'algoritmo:
  1. Aggiungere 0.5 al giorno giuliano dato JD
  2. Calcolare Z = I(JD) e F = JD - Z
  3. Se Z >= 2299161 calcolare alfa = I((Z - 1867216.25) / 36524.25) e A = Z + 1 + ALFA altrimenti porre A = Z
  4. Calcolare B = A + 1524, C = I((B - 122.1) / 365.25), D = I(365.25•C), E = I((B - D)/30.6001)
  5. Il giorno del mese, DD, è dato da: DD = B - D - I(30.6001•E) + F
  6. Il numero del mese, MM, è dato da: MM = E - 1 se E < 14. E' dato da MM = E - 13 se E >= 14
  7. Il numero dell'anno, YY, è dato da: YY = C - 4716 se MM > 2. E' dato da: YY = C - 4715 se MM <= 2
Ed ecco una routine BASIC che può realizzare l'algoritmo: 

100   '     DATMEEUS.BAS  -  Data civile da giorno giuliano
110 	DEFDBL  A-Z  :  CLS  :  DEF FNI(X) = SGN(X) * INT(ABS(X))
120   INPUT "Giorno giuliano:  ", JD
130 	JD = JD + .5
140 	Z = FNI(JD)  :  F = JD - Z
150 	IF Z >= 2299161# THEN ALFA = FNI((Z - 1867216.25#)/36524.25#) :                 	A= Z + 1 + ALFA - FNI(ALFA/4) ELSE A = Z
160   B = A + 1524 : C = FNI((B - 122.1)/365.25) : D = FNI(365.25	*C)       
      :  E = FNI((B - D) / 30.6001#)
170 	DD = B - D - FNI(30.6001#*E) + F
180 	IF E < 14 THEN MM = E - 1 ELSE MM = E - 13
190 	IF MM > 2 THEN YY = C - 4716 ELSE YY = C - 4715
200 	PRINT "Data civile =  "; DD;"/";MM;"/";YY
210 	END



TEMPO UNIVERSALE E TEMPO DINAMICO
Quello che con linguaggio corrente viene detto tempo medio di Greenwich (GMT), ufficialmente viene riconosciuto con il termine di tempo universale (TU), per gli anglosassoni UT. E' la scala temporale adottata per le necessità quotidiane. Abbiamo visto che questa scala è basata su un astro fittizio, il Sole medio, il quale a sua volta è basato sul moto di rotazione terrestre, immaginato uniforme.

Da qualche decina d'anni a questa parte i fisici hanno potuto accertare, tramite accurate misure di tempo (orologi atomici ed altri orologi ancora più precisi) che la velocità di rotazione della Terra presenta delle irregolarità che sono state determinate per il passato con una certa precisione, fino a risalire ad alcune centinaia di anni fa. Queste irregolarità però non possono essere previste per il futuro, se non a brevissima scadenza (poche decine di anni) a causa del loro carattere aleatorio. Utilizzando dunque orologi speciali di altissima precisione, quando se ne manifesta la necessità, si provvede ad aggiornare il tempo universale, riferendolo sempre alla velocità di rotazione della Terra.

A causa di quanto sopra, per gli astronomi si è manifestata la necessità di fare ricorso, per specifici scopi, ad una nuova conveniente scala temporale che tenga conto delle irregolarità che si sono avute finora. Ad esempio, per compilare una tabella di posizioni planetarie riferentesi a circa 2000 anni fa, non è possibile fare uso della scala temporale UT, perchè questa, come detto, è valida soltanto per l'epoca attuale.

Questa nuova scala temporale, unicamente riservata per calcoli astronomici che risalgano molto addietro nel tempo, oppure per effemeridi da usare attualmente ma che coprano diverse decine di anni, è stata denominata tempo dinamico, TD. Diciamo allora, con linguaggio approssimato, che un orologio che segni il tempo relativamente a questa nuova scala differirà, rispetto al tempo di un orologio basato sull'UT, di una quantità di secondi DT (delta T) continuamente variabile. Si ha cioè:    DT = TD - UT.

La scala temporale TD venne per la prima volta adottata con le Astronomical Ephemeris dal 1960 al 1983 (gli accertamenti sulle irregolarità del moto di rotazione terrestre sono abbastanza recenti), ma l'espressione Dynamical Time venne adottata nel 1984. Talvolta si usa per questa scala temporale la espressione di Ephemeris Time, (ET), per fare riferimento al fatto che si tratta di una scala temporale dedicata a segmenti temporali del passato.

Quindi gli istanti temporali ricavati da effemeridi che coprano un certo numero di anni sono in effetti istanti TD (quindi non istanti UT), ed andrebbero corretti della quantità DT per essere rapportati alla situazione contingente odierna. Ad esempio, secondo le effemeridi, il Sole si trovava al solstizio invernale all'istante TD = 05h 22m del 22 dicembre (astronomicamente: 1978, dicembre 22, 05h22m TD). Per avere il corrispondente istante UT (quello dei nostri orologi), al TD si deve sottrarre la Dt per quell'istante TD, che era di circa +29.5 secondi. Allora si ha:
GMT solstizio = UT = TD - DT = 05h 22m - 29.5 s = 05h 21m 30s.5.


UNA TABELLA DI VALORI DT
Le effemeridi (ad esempio, le International Ephemerides St.Michel) danno di solito i valori di DT per il primo giorno di ogni mese. La tabella che segue dà i valori del Dt in secondi, per l'inizio di alcuni anni (è tratta dall'Astronomical Almanach):


DT = TD - UT     (in secondi),    per l'inizio di alcuni anni
AnnoDT AnnoDT AnnoDT AnnoDT AnnoDT
1620+1241700+91780+171860+7.91940+24.3
16221151702917821718627.5194225.3
16241061704917841718646.4194426.2
1626981706917861718665.4194627.3
16289117081017881718682.9194828.2
1630+851710+101790+171870+1.61950+29.1
1632791712101792161872-1.0195230.0
1634741714101794161874-2.7195430.7
1636701716101796151876-3.6195631.4
1638651718111798141878-4.7195832.2
1640+621720+111800+13.71880-5.41960+33.1
164258172211180213.11882-5.2196234.0
164455172411180412.7 1884-5.5196435.0
164653172611180612.51886-5.6196636.5
164850172811180812.51888-5.8196838.3
1650+481730+111810+12.51890-5.91970+40.2
165246173211181212.51892-6.2197242.2
165444173412181412.51894-6.4197444.5
165642173612181612.51896-6.1197646.5
165840173812181812.31898-4.7197848.5
1660+371740+121820+12.01900-2.71980+50.5
166235174212182211.419020.0198252.2
166433174413182410.61904+2.6198453.8
16663117461318269.61906+5.4198654.9
16682817481318288.619087.7198855.8
1670+261750+131830+7.51910+10.51990+56.9
16722417521418326.6191213.4199258.3
16742217541418346.0191416.0199461.0
16762017561418365.7191618.2199663.0
16781817581518385.6191820.2199865.0
1680+161760+151840+5.71920+21.22000+67.0
16821417621518425.9192222.4200270.0
16841317641518446.2192423.5200473.0
16861217661618466.5192623.9200675.0
16881117681618486.8192824.3200877.0
1690+101770+161850+7.11930+24.02010+80.0
1692917721618527.3193223.9--
1694917741618547.5193423.9--
1696917761718567.7193623.7--
1698917781718587.8193824.0--


Per epoche al di fuori dell'intervallo di questa tabella si può ricorrere ad un valore approssimato di DT, ottenibile da una di queste formule (J. Meeus):
  • Dt = 102.3 + 123.5•T + 32.5•T•T
  • Dt = -15 + (JD - 2382148)2 / 41048480
dove T, tempo secolare, è in secoli giuliani, a partire dalla Standard Epoch 2000.0 (vedere paragrafi successivi).
Va detto che, facendo uso di queste formule, si possono avere errori massimi dell'ordine delle 2 ore, per calcoli risalenti fino al 4000 a.C.



DUE SEMPLICI ESEMPI
Conversione da TD a UT - Secondo le international Ephemerides 1900 - 2000, si è avuta Luna piena all'istante TD = 19h 59m del 29.6.1950. Calcolare il corrispondente istante UT, tramite la tabella di cui sopra.
Soluzione: per l'inizio dell'anno 1950, dalla tabella si ricava DT = +29.1 s. Allora:
UT = TD - DT = 19h 59m - 29.1s = 19h 58m 30.9s del 29.6.1950

Conversione da UT a TD - Supponendo di disporre di effemeridi che risalgano all'anno 44 a.C., vogliamo trarre da esse la longitudine di Marte per l'istante UT = 10h 00m del 15 marzo dell'anno 44 a.C. (-43, Marzo, 15.416666667, JD = 1705425.916666667). Calcolare il TD con il quale entrare nelle effemeridi per estrarre la longitudine di Marte.
Soluzione: applichiamo la seconda delle due formule di cui sopra.
DT = -15 + (1705425.916666667 - 2382148)2 / 41048480 = +11156.4 s = 3h 05m 56s.4 TD = 10h 00m 00s + 3h 05m 56s.4 = 13h 05m 56s.4 del 15 marzo del 44 a.C.


SECOLO GIULIANO, STANDARD EPOCH, TEMPO SECOLARE
Con il termine di secolo giuliano si intende l'intervallo di tempo di 36525 giorni solari medi, cioè il numero di giorni medi risultanti da 365.25•100.
In alcuni testi astronomici, quando in riferimento al giorno giuliano viene usata l'espressione JD (Julian day), allora quell'istante è riferito alla scala temporale UT (Universal Time). Quando invece si vuole fare riferimento alla scala temporale del tempo dinamico TD (o anche ET), allora si fa uso dell'espressione JDE (Julian Day Ephemeris). Si considerino questi due istanti:
Istante 1: 1955 maggio 25.5 UT, esprimibile con JD 2435253.0
Istante 2: 1955 maggio 25.5 TD, esprimibile con JDE 2435253.0
Si tratta, come spiegato, di due istanti diversi, separati della quantità DT = +31 secondi circa (valore ricavabile dalla tabella di cui sopra), con l'istante 2 in anticipo sull'istante 1.
(Tranne che per gli anni dal 1871 al 1901, un istante dato in UT è in ritardo rispetto all'istante dato in TD con la stessa espressione numerica. Ad esempio, l'istante 1930 gennaio 12 UT si è avuto circa 24 secondi dopo l'istante 1930 gennaio 12 TD).




Esercitazioni    (5)

Per il giorno 25.9.2003 e per la località di New York (Lat. 40º40' N, Long. 4h 55m W, fuso orario in vigore: 6W), calcolare i valori del tempo sidereo locale ts per le seguenti ore locali:
(1) 3h 24m, (2) 9h 36m, (3) 15h 28m, (4) 21h 17m. sapendo che:
- Ts (Greenwich) alle 00h GMT (25.9.2003) = 00h 13m 36s
- Ts (Greenwich) alle 00h GMT (26.9.2003) = 00h 17m 33s
- Variazione media giornaliera tempo sidereo = 3m 56s (come noto) In ogni schema grafico (proiezione ortografica equatoriale) indicare anche la simultanea posizione del Sole medio.


Diamo la soluzione per il caso (1)

Ora locale ______   03h 24m 00s del 25.9.2003
Diff. GMT _____ + 06h
                             ---------------
GMT _________    09h 24m 00s del 25.9.2003

Calcolo variazione tempo sidereo per 9h 24m
Variazione giornaliera tempo sidereo: 236s
1440m : 236s = 564m : X    da cui X = 1m 32s

GMT __________ 09h 24m 00s
Ts 00h GMT ____ 00h 13m 36s
Variaz. ts _______        01m 32s
                             ---------------
Ts _____________ 09h 39m 08s
Long. N.Y. ___ (-)  04h 55m 00s
                             ---------------
ts ______________ 04h 44m 08s





GENERALITA’ SUI MOTI DELLA LUNA
Il diametro apparente della Luna, cioè l’angolo sotto il quale il disco lunare è visto dalla Terra, varia tra i valori approssimati di 29’ 20” e 33’ 50”. Il diametro apparente del Sole, invece, varia tra i valori 31’ 31” e 32’ 36”. Il disco lunare, quindi, appare talvolta più piccolo del più piccolo disco solare, e talvolta più grande del più grande disco solare. Questo fatto, evidentemente dovuto alla variabilità delle distanze di Luna e Sole dalla Terra, è quello che (come vedremo in seguito) (1) rende possibile le eclissi totali di Sole e (2) talvolta fa sì che un'eclisse di Sole sia anulare, anzichè totale.

Incominciando ad affrontare i moti della Luna, diciamo che, in prima approssimazione, essa gira intorno alla Terra secondo le leggi di Keplero, quindi descrivendo un ellisse di eccentricità circa 1/18 circa, ellisse di cui la Terra occupa uno dei fuochi, a una distanza media di 384.000 Km. Ma quest’ellisse, particolarmente per effetto dell’attrazione solare, si sposta e deforma continuamente per cui i suoi punti non giacciono tutti nello stesso piano. La forte eccentricità causa anche un altro aspetto di irregolarità notevole nel moto della Luna: una forte variazione della sua velocità. Mentre la massima velocità orbitale angolare della Terra è soltanto del 7% circa più grande della minima, la massima velocità orbitale angolare della Luna è di ben il 25% circa più grande della minima.

Se poi volessimo avere un’idea abbastanza soddisfacente dell’orbita lunare rapportandola all’orbita terrestre intorno al Sole, rappresentando quest’ultima con un cerchio di raggio un metro (anziché, come correttamente si dovrebbe, con un ellisse), l’orbita lunare dovrebbe essere rappresentata con una spirale che non si discosti dall’orbita terrestre più di 2.5 millimetri. Vediamo quindi che, compiendo la Luna circa 12 giri durante un’orbita terrestre (circa 3 giri in un quarto di orbita terrestre), il percorso della Luna assume un andamento spiraliforme molto “stirato” rispetto all’orbita terrestre. Questo “stiramento” è respondsabile del fatto che l’orbita lunare rivolge la sua concavità sempre verso il Sole.



DIFFERENTI RIVOLUZIONI LUNARI
Rivoluzione siderea è detto il tempo impiegato dalla Luna a compiere un giro completo della volta celeste intorno alla Terra. Equivale a 27.32166 giorni solari medi. E’ l’intervallo tra due congiunzioni successive della Luna con una stella fissa (evidentemente supposta priva di moto proprio). Rivoluzione tropica è invece l’intervallo che intercorre tra due congiunzioni successive della Luna con il punto ^. E’ leggermente più corta della siderea (il punto vernale “va incontro” alla Luna di circa 7 secondi, a causa della precessione terrestre) . Ha la durata di 27.32158 giorni solari medi.
Rivoluzione sinodica, detta anche mese sinodico, o anche, più semplicemente, mese lunare, è l’intervallo durante il quale la Luna esegue tutte le sue modificazioni di aspetto (intervallo tra due congiunzioni eclittiche con il Sole). Durata 29.53059 giorni solari medi.
Si dice età della Luna il numero di giorni e frazione trascorsi dall’ultima Luna nuova.



TRANSITI MERIDIANI DELLA LUNA
Giorno lunare è l’intervallo di tempo che intercorre tra due passaggi consecutivi della Luna allo stesso meridiano. In una intera lunazione le durate dei giorni lunari sono differenti. In media un giorno lunare è più lungo di uno solare di circa 50 minuti. Infatti, durante una rivoluzione sinodica la Luna esegue sulla volta celeste evidentemente un giro in meno del Sole. Allora: 28.5306 giorni lunari = 29.5306 giorni solari = (28.5306 + 1) giorni solari.
Dividendo entrambi i membri per 28.5306 si ha:
1 giorno lunare = 1 giorno solare + 1/28.5306 = 24h + 24h / 28.5306 = 24h + 1440m / 28.5306 = 24h 50m

Segue che il passaggio della Luna al meridiano di un luogo ritarda ogni giorno in media 50 minuti. E allora può avvenire che un dato giorno la Luna non transiti al meridiano. Infatti, se la Luna passa al meridiano poco prima della mezzazotte di un dato giorno (per esempio, alle 23h 40m del 20.5, l’indomani il passaggio avverrà alle: 23h 40m + 50m = 24h 30m del 21.5, cioè alle 00h 30m del 22.5. Quindi il 21 maggio non si è avuto alcun transito della Luna al meridiano. Questo fenomeno si verifica in prossimità del plenilunio.



ORBITA DELLA LUNA
Anche una grossolana osservazione, eseguita senza strumenti di misura, mostra che la Luna ha un forte moto proprio sulla sfera celeste. Compiendo la Luna un intero giro di volta celeste in un mese lunare, 29.5 giorni circa, essa avrà uno spostamento effettivo verso est rispetto alle stelle fisse di circa 13º al giorno. Siccome il Sole ha uno spostamento apparente verso est di circa un grado al giorno, allora la Luna avrà uno spostamento verso est rispetto al Sole di circa 12º al giorno. Si noti che questo spostamento è reale e non apparente come quello del Sole.

Se su un globo celeste sul quale sia segnata l’eclittica E-E’ segnamo le successive posizioni della Luna durante un mese lunare, noteremmo che la Luna descrive all’incirca un circolo massimo L-L’, che è la proiezione sulla sfera celeste della effettiva orbita lunare. Abbiamo detto all’incirca perché la Luna è molto influenzata dal Sole e la sua orbita subisce delle forti perturbazioni. Non tenendo conto di queste perturbazioni, possiamo dire che la Luna descrive tra le stelle un circolo massimo che è inclinato in media di circa 5º 09’ rispetto all’eclittica. Questa obliquità della Luna subisce delle piccole oscillazioni in un periodo di circa sei mesi.
I punti di intersezione tra orbita lunare ed eclittica sono i cosiddetti nodi lunari. Quando la luna passa dall’emisfero sud a quello nord, incontra l’eclittica nel nodo ascendente, . Quando invece, dopo 14 giorni circa, passa dall’emisfero nord a quello sud, incontra l’eclittica nel nodo discendente,



RETROGRADAZIONE DEI NODI LUNARI
Vi è un fenomeno di precessione anche per l’asse polare PL-PL’ dell’orbita lunare. Ciò fa si che, similmente ai punti ^ e W dell’eclittica, si abbia un movimento di retrogradazione anche per i nodi lunari. Questi compiono una rivoluzione completa di sfera celeste in 6793.39 giorni, 18 anni e mezzo circa (1º.5 circa per mese lunare, circa 3 primi di arco al giorno). La conseguenza più notevole di questo fenomeno è la continua variazione di declinazione della Luna da una lunazione all’altra. Nell’arco di tempo di 18 anni e mezzo si passa da una Lunazione con una variazione in declinazione nord-sud minima, a una lunazione con variazione massima. Vediamo di dare una breve spiegazione qui di seguito.

Quando il nodo ascendente dell’orbita lunare si trova in prossimità del punto ^, l’orbita della Luna in quell’epoca è quella LL’ della figura 70. Come si vede, la declinazione raggiunge il massimo valore assoluto di 23º 26’ + 5º 09’ = 28º 35’ In quelle lunazioni si ha la massima escursione in declinazione (da 28º 35’ N a 28º 35’ S, circa).

Quando invece, dopo circa nove anni, in seguito alla retrogradazione dei nodi lunari, è il nodo discendente a trovarsi in prossimità del punto ^, figura 71, allora, durante la lunazione di quell’epoca si ha la minima escursione in declinazione, da 18º 18’ N a 18º 18’ S, circa.
Durante le lunazioni intermedie tra queste due epoche, evidentemente le escursioni in declinazione della Luna saranno intermedie, diminuendo progressivamente da un massimo di circa 57º, fino a un minimo di circa 36º.5, quindi aumentando progressivamente fino al nuovo massimo.


Le figure 72 e 73 mostrano quale sia la corrispondenza tra escursione in declinazione ed escursione in azimut del punto del sorgere della Luna durante un ciclo completo di retrogradazione dei nodi lunari (di 18 anni e mezzo). All’epoca della lunazione che si compie con la massima escursione in declinazione, si ha anche massima escursione in azimut del punto del sorgere della Luna (tra A e B di figura 72).

Invece all’epoca della lunazione che si compie con la minima escursione in declinazione, si ha anche minima escursione in azimut del punto del sorgere della Luna (tra A’ e B’ di figura 73).

(Abbiamo presentato al lettore questa associazione tra escursione in declinazione ed escursione in azimut della Luna per rammentargli che lo studio sistematico di questa associazione, unito alla osservazione sistematica delle posizioni lunari, furono i due filoni di indagine che consentirono agli antichi Babilonesi di pervenire al padroneggiamento dei cicli lunari, con i risultati (1) di prevedere le eclissi lunari e (2) di ottenere un soddisfacente schema calendariale lunisolare.



RIVOLUZIONI DRACONITICA E ANOMALISTICA
La rivoluzione draconitica è l’intervallo di tempo che intercorre tra due passaggi consecutivi della Luna al suo nodo ascendente. Siccome a causa della precessione il nodo ascendente si sposta verso ovest di circa 1º.5 in un mese lunare, la rivoluzione draconitica è più corta della siderea.
Tra i moti della Luna va anche presa in considerazione la rivoluzione anomalistica. Deriva dal fatto che la linea congiungente gli apsidi dell’orbita lunare (apogeo e perigeo lunari), similmente alla linea degli apsidi dell’orbita terrestre, non è fissa nello spazio ma ruota in senso diretto, compiendo un giro intero della sfera celeste in 3232.59 giorni, per cui la longitudine del perigeo lunare aumenta giornalmente di circa 7’ di arco. Rivoluzione anomalistica è dunque l’intervallo che intercorre tra due passaggi consecutivi della Luna al perigeo lunare.

Ecco un elenco delle rivoluzioni lunari, in ordine di durata:
Sinodica, due successive congiunzioni con il Sole _________________    29d 12h 44m 02s.8
Anomalistica, due successive congiunzioni con perigeo lunare _______    27d 13h 18m 33s.1
Siderea, due successive congiunzioni con una stella fissa ___________    27d 07h 43m 11s.5
Tropica, due successive congiunzioni con Punto ^ _______________    27d 07h 43m 04s.7
Draconitica, due successive congiunzioni con nodo lun. ascend. _____    27d 05h 05m 35s.8


MOTI DI LIBRAZIONE DELLA LUNA
Si dice comunemente che la Luna rivolge sempre lo stesso emisfero alla Terra perché il periodo del suo moto di rotazione è uguale al periodo di rivoluzione attorno alla Terra. In effetti le cose non stanno esattamente così, nel senso che dalla Terra è visibile un po' più di un emisfero lunare. Ciò è dovuto al fatto che la Luna è dotata dei cosiddetti moti di librazione, che si distinguono in librazione in latitudine e librazione in longitudine.

La figura 74 illustra il moto di librazione in latitudine. Questa è dovuta al fatto che l’asse PL-PL’ di rotazione della Luna non è perpendicolare al piano dell’orbita lunare L-L’, ma è inclinato rispetto all’asse di detto piano orbitale di circa 6º 40’. Ciò si traduce nel fatto che quando la Luna si trova alla posizione A della sua orbita, dalla Terra T è visibile anche la regione a di calotta polare lunare sud, mentre quando, dopo circa 14 giorni, la Luna si trova alla posizione B, dalla Terra è visibile anche la regione b di calotta polare lunare nord.

Vediamo ora il moto di librazione in longitudine. Esso è dovuto sostanzialmente al fatto che l’orbita lunare è ellittica e non circolare. Se fosse circolare, non si avrebbe librazione in longitudine. Mentre la rotazione della Luna sul suo asse si compie con velocità angolare costante (un giro esatto per ogni rivoluzione siderea), lungo la sua orbita la Luna si muove con velocità variabile (secondo la legge di Keplero delle aree).
Riferendoci alla figura 75, diciamo che se in un certo intervallo di tempo la Luna ha percorso l’arco di orbita da A a B, corrispondente all’angolo a sulla sfera celeste, con tutta probabilità essa, nello stesso intervallo di tempo non avrà ruotato su sé stessa dello stesso angolo a. Per spiegarci meglio, diciamo che se nella posizione A, un certo oggetto C veniva visto da Terra sulla congiungente centro Terra - centro Luna, al termine dell’intervallo di tempo è molto probabile che quell’oggetto non sia più visto sulla congiungente i centri dei due astri, ma un po’ spostato, o in C1 o in C2.



IL FENOMENO DELLA LUCE CINEREA
Consiste nel fatto che, in prossimità del novilunio, quando la Luna assume l’aspetto di una falce sottilissima, talvolta accade che il resto del disco lunare, anziché essere completamente invisibile come nelle altre fasi, appaia dalla Terra con una tinta grigiastra, che viene detta luce cinerea. Si tratta di luce solare riflessa dalla Terra alla Luna. Infatti, si deve tenere presente che dalla Luna sono osservabili fasi terrestri perfettamente simili e speculari alle fasi lunari, per cui durante il novilunio la Terra si trova nella fase di "Terra piena", riflettendo tutta la sua luce alla Luna, che quindi manifesta quel fenomeno di luce grigiastra.



NOZIONI ELEMENTARI SULLE ECLISSI DI SOLE E DI LUNA
Le eclissi di Sole sono prodotte dal corpo della Luna che, interponendosi tra la Terra e il Sole, nasconde in tutto o in parte il disco solare. Le eclissi di Luna, invece, si hanno quando la Luna viene a capitare, completamente o in parte, nel cono d’ombra che la Terra “si trascina continuamente appresso”.


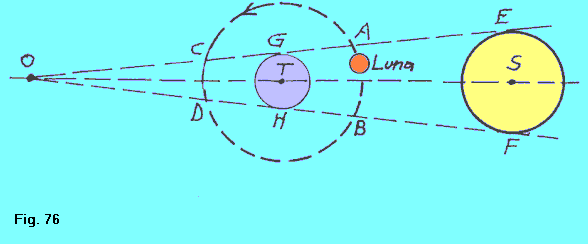Si tracci il cono OCGEFHD, circoscritto al Sole e alla Terra. La parte di tale cono OCGHD, compresa tra la Terra e il vertice O, è detta cono d’ombra terrestre. In esso non può penetrare alcun raggio solare. La sua lunghezza, TO, è di circa 216 raggi terrestri e il suo asse giace sul piano dell’eclittica.. (Si osservi che in figura 76 il percorso della Luna è stato tracciato circolare, per semplificare. Questa è stata una prima approssimazione. Ma un vero e proprio errore è dato dall’aver tracciato l’orbita circolare della Luna come se fosse giacente sul piano del foglio. Noi sappiamo invece che il piano orbitale lunare è inclinato di circa 5º sull’eclittica. Ora, siccome dalla figura il piano dell’eclittica è un piano perpendicolare al piano del foglio e passante per la linea OTS, la traccia corretta del piano orbitale lunare dovrebbe essere una linea passante per T, centro della Terra, e inclinata rispetto alla OTS di circa 5º. Quindi, quella traccia circolare ACDB ha uno scopo semplicemente indicativo).

Si ha dunque eclisse di Sole quando la Luna, capitando tra la Terra e il Sole, come nel tratto ALB, nasconde totalmente o parzialmente il disco solare. Come si vede dalla figura 76, ciò si verifica al novilunio. Si ha invece eclisse di Luna quando la Luna capita nel cono d’ombra terrestre, come nel tratto CD, potendo in tal caso rimanere oscurata (cioè non vista dalla Terra) parzialmente o totalmente, pur essendo in una fase di plenilunio, come si vede dalla figura.

Se il piano dell’orbita lunare coincidesse con il piano dell’eclittica, si osserverebbe un’eclisse di Sole ad ogni novilunio ed una di Luna ad ogni plenilunio. Siccome, come detto sopra, l’inclinazione dell’orbita lunare rispetto al piano dell’eclittica è di circa 5º, avviene che in genere, al novilunio la Luna passa “sopra” o “sotto” il Sole, senza impedirne quindi la visione, e al plenilunio generalmente non entra nel cono d’ombra terrestre, rimanendo così visibile. Potremmo dire che le eclissi si verificano quando, con Luna e Sole alle sizigie (cioè nelle fasi di novilunio e plenilunio), le declinazioni dei due astri sono tali da collocarli entrambi in prossimità dei nodi lunari.

Si potrebbe dimostrare con calcoli trigonometrici che affinchè si verifichi una eclisse di Luna, anche parziale, la distanza angolare Sole-nodo deve essere non superiore a circa 10º, mentre perché si abbia una eclissi totale di Luna, la detta distanza non dev’essere superiore ai 5º circa. Per una eclissi di Sole, invece, è necessario che la distanza angolare Sole-nodo sia minore di 15º circa. Le eclissi di Sole sono quindi più frequenti di quelle di Luna.

Si dice anno delle eclissi il tempo impiegato dal Sole per effettuare due passaggi consecutivi al nodo ascendente lunare. Poiché il nodo retrograda di circa 19º in un anno, il Sole impiega circa 19 giorni in meno dell’anno solare per transitare allo stesso nodo. Pertanto, l’anno delle eclissi è di 365.25 - 19 = 346 giorni circa. Si tenga presente che le eclissi sono distribuite in due gruppi, nelle due cosiddette stagioni delle eclissi, distanti circa sei mesi l’una dall’altra.

E’ opportuno che il lettore abbia chiaro un aspetto importante di differenziazione tra le eclissi di Sole e quelle di Luna. L’eclisse di Luna si ha, come già detto, per l’entrata della Luna nel cono d’ombra terrestre. Ora, questo fenomeno avviene indipendentemente dalla posizione dell’osservatore sulla Terra, per cui tutti gli osservatori sulla Terra vedono inizio e fine del fenomeno dell’eclissi di Luna contemporaneamente. Le cose vanno diversamente per le eclissi di Sole perché, come già detto, per questo fenomeno bisogna prendere in considerazione il cono d’ombra lunare che, in particolari condizioni di allineamento, va a “spazzare” la superficie terrestre. Occorre tenere presente che: (1) le condizioni di allineamento dei tre corpi durano in genere poche ore e (2) in quelle poche ore è soltanto una striscia di superficie terrestre in cui si ha l’eclisse totale. (Questa è la ragione per la quale, malgrado le eclissi di Sole siano più frequenti di quelle di Luna, per una stessa località sono queste ultime ad essere più frequenti).

Come si vede con qualche approssimazione dalla figura 77, una eclisse di Sole è visibile dalla Terra solo lungo una fascia di circa 200 Km di diametro, mentre la simultanea eclissi parziale è visibile da un’area estesa alcune migliaia di Km attorno alla fascia di totalità. Il lettore comprenderà inoltre che la rotazione terrestre durante la fase di eclisse farà sì che questa abbia luogo a istanti diversi lungo la fascia sia di totalità che di eclisse parziale.


ECLISSI DI SOLE
Può essere opportuno spendere ancora qualche parola sulle eclissi di Sole, essendo quelle di Luna di interesse minore. Le eclissi di Sole si hanno ogni volta che Sole e Luna si trovano (entrambi) in prossimità di uno stesso nodo. Si hanno, come già detto, durante la fase di novilunio.
Una eclisse totale di Sole può essere osservata da una fascia di superficie terrestre della larghezza di circa 200 Km, mentre la corrispondente eclisse parziale risulta visibile nell’ambito di una ulteriore fascia di circa 35º, intorno alla fascia di totalità.
La figura mostrano che la possibilità di avere eclisse totale (oltre che richiedere le due condizioni già menzionate) è tanto più grande quanto più l’allineamento dei tre oggetti avviene con la Luna prossima al perigeo (Luna alla minima distanza da Terra). In tal caso è probabile che il diametro apparente della Luna, maggiore di quello del Sole, produca la condizione di totalità. Quando invece l’allineamento avviene con Luna prossima all’apogeo allora, (diametro apparente della Luna inferiore a quello del Sole) è probabile avere la condizione di eclisse anulare: attorno al disco oscuro della Luna appare, al massimo dell’eclisse, un anello luminosissimo.




CONVERSIONE DA COORDINATE ECLITTICHE A EQUATORIALI
Proponiamo questa semplicissima procedura per convertire coordinate eclittiche (Lat, Long) in equatoriali (a, d), facendola seguire da una routine BASIC di implementazione della stessa.

Con riferimento alla fig. 79, dal triangolo rettangolo PYH1 si ha:
cos(90 - Long) = ctg(A)•ctg(90 - Lat)
sen(Long) = ctg(A)•tan(Lat)
ctg(A) = sen(Long)/tan(Lat)
tan(A) = tan(Lat)/sen(Long)

Dallo stesso triangolo si ha:
cos(R) = sen(90-Lat)•sen(90-Long)
cos(R) = cos(Lat)•cos(Long)

Essendo e l'obliquità dell'eclittica, si ha:
B = A + e

Dal triangolo PYH2 si ha:
cos(B) = ctg(R)•ctg(90-a)
cos(B) = ctg(R)•tan(a)
tan(a) = cos(B)/ctg(R)
tan(a) = cos(B)•tan(R)

Infine, dallo stesso triangolo si ha:
cos(90-d = sen(B)•sen(R)
sen(d) = sen(B)•sen(R)


Ed ecco la routine BASIC (in essa, si noti che anzichè aversi, come da procedura, B = A + e, si è posto A = A + e, [A = A + OB]) : 

100     '    ECLEQUAT.BAS   -   convers. di coord. eclitt. in equat
105     GOSUB 140
110     AR = FND(AR) : DE = FND(DE)
115     PRINT "Ascensione retta=        ";AR
120     PRINT "Declinazione=            ";DE
125     INPUT "Continuare  ?  (s/n)     ",R$
130     IF R$="S" OR R$="s" THEN 105
135     END
140     KEY OFF : CLS : DEFDBL A-Z
145     PI = 3.14159265359#  :  OB = .4092254042625427#
150     '       da gradi a radianti
155     DEF FNR(X) = X/180*PI
160     '       da radianti a gradi
165     DEF FND(X) = X/PI*180
170     '       funzione arcsin(x)
175     DEF FNAS(X) = ATN(X/SQR(1-X*X))
180     '       funzione arccos(c)
185     DEF FNAC(X) = ATN(SQR(1-X*X)/X)
190     '
195     PRINT
200     INPUT "Longitudine celeste (GGG.decimale):   ", LONG
205     IF LONG = 0 THEN LONG = .0000000000001#
210     IF LONG = 180 THEN LONG = 179.9
215     INPUT "Latitudine celeste: (GG.decimale):   ", LAT
220     PRINT
225     '   conversione di coordinate eclittiche in equatoriali
230     '   input:          LAT, LONG (lat. e long. in GGG.decimale)
235     '   output:         DE, AR  (decl. e asc.r. in GGG.decimale)
240     LONG = FNR(LONG)
245     LAT = FNR(LAT)
250     A=ATN(TAN(LAT)/SIN(LONG))
255     IF SIN(LONG)<0 THEN A=A+PI
260     R=FNAC(COS(LAT)*COS(LONG))
265     IF COS(LONG)<0 THEN R=R+PI
270     A=A+OB
275     AR=ATN(COS(A)*TAN(R))
280     IF AR<0 THEN AR=AR+PI
285     IF COS(A)<0 THEN AR=AR+PI
290     DE=FNAS(SIN(A)*SIN(R))
295     RETURN
300     '       *****************************************
CONVERSIONE DA COORDINATE EQUATORIALI IN ECLITTICHE
Ecco la conversione inversa. Si faccia riferimento sempre alla figura 79. Però, in questo caso, quello che era chiamato angolo B, adesso è l'angolo A, e viceversa.

Dal triangolo rettangolo PYH2 si ha:
cos(90- a) = ctg(A)•ctg(90 - d)
sen(a) = ctg(A)•tan(d)
ctg(A) = sen(a)/tan(d)
tan(A) = tan(d)/sen(a)

Dallo stesso triangolo si ha:
cos(R) = sen(90-d)•sen(90-a)
cos(R) = cos(d)•cos(a)

Essendo e l'obliquità dell'eclittica, si ha:
B = A - e

Dal triangolo PYH2 si ha:
cos(B) = ctg(R)•ctg(90-Long)
cos(B) = ctg(R)•tan(Long)
tan(Long) = cos(B)/ctg(R)
tan(Long) = cos(B)•tan(R)

Infine, dallo stesso triangolo si ha:
cos(90-Lat) = sen(B)•sen(R)
sen(Lat) = sen(B)•sen(R)


Ed ecco la routine BASIC. In essa, anzichè porre B = A - e, come da procedura, si è posto A = A - e, (A = A - OB). 

100     '       EQUATECL.BAS - convers. di coord. equat. in eclitt.
105     GOSUB 140
110     LONG= FND(LONG) : LAT = FND(LAT)
115     PRINT "Longitudine=        ";LONG
120     PRINT "Latitudine=         ";LAT
125     INPUT "Continuare  ?  (s/n)     ",R$
130     IF R$="S" OR R$="s" THEN 105
135     END
140     KEY OFF : CLS : DEFDBL A-Z
145     PI = 3.14159265359#  :  OB = .4092254042625427#
150     '       da gradi a radianti
155     DEF FNR(X) = X/180*PI
160     '       da radianti a gradi
165     DEF FND(X) = X/PI*180
170     '       funzione arcsin(x)
175     DEF FNAS(X) = ATN(X/SQR(1-X*X))
180     '       funzione arccos(c)
185     DEF FNAC(X) = ATN(SQR(1-X*X)/X)
190     '
195     PRINT
200     INPUT "Ascensione retta (GGG.decimale):   ", AR
205     IF AR = 0 THEN AR = .0000000000001#
210     IF AR = 180 THEN AR = 179.9
215     INPUT "Declinazione      (GG.decimale):   ", DE
220     PRINT
225     '       conversione di coordinate equatoriali in eclittiche
230     '       input:     DE, AR (decl.,asc.r. in GGG.decimale)
235     '       output:    LAT, LONG (latit. longit. in GGG.decimale)
240     AR = FNR(AR)
245     DE = FNR(DE)
250     A=ATN(TAN(DE)/SIN(AR))
255     IF SIN(AR)<0 THEN A=A+PI
260     R=FNAC(COS(DE)*COS(AR))
265     IF COS(AR)<0 THEN R=R+PI
270     A=A-OB
275     LONG=ATN(COS(A)*TAN(R))
280     IF LONG<0 THEN LONG=LONG+PI
285     IF COS(A)<0 THEN LONG=LONG+PI
290     LAT=FNAS(SIN(A)*SIN(R))
295     RETURN
300     '       *****************************************
>




SOLUZIONI ESERCIZI    (1)

(Sono date le soluzioni della maggior parte degli esercizi)



1. Lat. 40º N


2. Lat. 30º S /TD>


2.2    244º 49' 17".1 = (177.1/60 + 49) / 60 + 244
        Con calcolatrice, senza uso del tasto <º'">:                              ==>    244º.821416667
        Con uso del tasto <º'">:     2,4,4,<º'">,4,9,<º'">1,7,.,1,<º'">    ==>    244º.821416667

2.3    128º 24' 49" = (49/60 + 24) / 60 + 128
        Con calcolatrice, senza uso del tasto <º'">:                             ==>    128º.413611111
        Con uso del tasto <º'">:    1,2,8,<º'">,2,4,<º'">,4,9,<º'">        ==>    128º.413611111

2.4    66º 16' 19" = (19/60 + 16)/60 + 66
        Con calcolatrice, senza uso del tasto <º'">:                             ==>     66º.271944444
        Con uso del tasto <º'">:      6,6,<º'">,1,6,<º'">,1,9,<º'">         ==>     66º.271944444


3.1       277º 44' 53".44 +
             98º 37' 22".37
            ------------------
           376º 22' 15".81
      (-) 360º
             ------------------
            16º 22' 15".81


3.2        12º 29'.8 +
              3º 54'.7
            ------------
            16º 24'.5


4.1       248º 25' 24".18       Si potrebbe anche eseguire così:     247º 84' 84".18
       (-) 117º 44' 55".92                                                     (-) 117º 44' 55".92
            -------------------                                                         -------------------
            130º 40' 28".26                                                          130º 40' 28".26



4.2        14º 35' 29".64       Si potrebbe anche eseguire così:        14º 35' 29".64
        (-) 28º 12' 31"                                                             (-) 27º 72' 31"
            -----------------                                                              ------------------
        (-) 13º 37' 01".36                                                         (-) 13º 37' 01".36
      (+) 360º                                                                      (+) 359º 59' 60"
            -----------------                                                             -------------------
           346º 22' 58".64                                                            346º 22' 58".64





Soluzioni esercizi     (2)

(Sono date le soluzioni della maggior parte degli esercizi)

Esercizio 1a - Latitudine nord                
      T .............        18º 47'.7
    + Long .......    +177º 25'.2
                             ------------
      t ..............       196º 12'.9


Esercizio 1b - Latitudine sud                          
      T .............        229º 34'.5
    + Long .......   (-)   48º 12'.5
                             -------------
      t ..............         181º 22'.0


Esercizio 2a - Vega - Emisfero nord                
     ts ............       235º 27'.4
    - a ...........       278º 51'.8
                            ------------
     t ..............      - 43º 24'.4
    + 360º ......    + 359º 60'
                            ------------
     t ..............       316º 35'.6


Esercizio 2b - Antares - Emisfero sud                
     ts ............       235º 27'.4
    - a ...........     - 246º 40'.5
                           -------------
     t ..............      - 11º 13'.1
    + 360º ......    + 359º 60'
                            -------------
     t ..............       348º 46'.9





Soluzioni esercizi    (3)

(Sono date le soluzioni della maggior parte degli esercizi)

Esercizio 1a: Latitudine 40º N
Azimut 55º, altezza 30º

Esercizio 1b: Latitudine 40º S
Azimut 130º, altezza 50º

Esercizio 2a: Latitudine 45º N
Agolo orario 230º, declinazioe 55º N

Esercizio 2b: Latitudine 45º S
Agolo orario 330º, declinazioe 15º S

Esercizio 3a: Latitudine 50º N
Tempo sidereo 3h 30m (52º 30')

Esercizio 3b: Latitudine 50º N
Tempo sidereo 20h (300º)





Soluzioni esercizi    (4)

(Sono date tutte e tre le soluzioni)

   ts = 122º

   ts = 244º

   ts = 296º



Soluzioni esercizi    (5)

[Sono date le soluzioni per i casi (2) e (4) ]


Ora locale ______   09h 36m 00s del 25.9.2003
Diff. GMT _____ + 06h
                             ---------------
GMT _________    15h 36m 00s del 25.9.2003

Calcolo variazione tempo sidereo per 15h 36m
Variazione giornaliera media tempo sidereo: 236s
1440m : 236s = 936m : X    da cui X = 2m 33s

GMT __________ 15h 36m 00s
Ts 00h GMT ____ 00h 13m 36s
Variaz. ts _______        02m 33s
                             ---------------
Ts _____________ 15h 52m 09s
Long. N.Y. ___ (-)  04h 55m 00s
                             ---------------
ts ______________ 10h 57m 09s


Ora locale ______   21h 17m 00s del 25.9.2003
Diff. GMT _____ + 06h
                             ---------------
GMT _________    03h 17m 00s del 26.9.2003

Calcolo variazione tempo sidereo per 3h 17m
Variazione giornaliera media tempo sidereo: 236s
1440m : 236s = 197m : X    da cui X = 00m 32s

GMT __________ 03h 17m 00s
Ts 00h GMT ____ 00h 17m 33s
Variaz. ts _______        00m 32s
                             ---------------
Ts _____________ 03h 35m 05s
Long. N.Y. ___ (-)  04h 55m 00s
                             ---------------
ts ______________ 22h 40m 05s