|
DAL SOLE NON SOLO ENERGIA Ecco un sintetico elenco dei benefici che riceviamo dal Sole:
|
|
NUCLEO DEL SOLE - FUSIONE NUCLEARE Fu soltanto verso la fine degli anni Trenta del secolo scorso che il fisico tedesco H. Bethe scoprì che l’energia solare era dovuta alle reazioni di fusione nucleare all’interno di sole e stelle. Nel nucleo del Sole ha sede la sua centrale energetica. Ha un raggio di circa un quinto di quello del Sole. In esso è prodotta l’80% dell’energia totale. La temperatura del nucleo varia da 10•106 K e 15•106 K. La densità raggiunge un valore di 150 volte quella dell’acqua. In queste condizioni, i nuclei di elementi leggeri possono giungere, per la compressione che subiscono, a distanze talmente piccole da produrre il fenomeno della fusione nucleare. |
Il 98% dell’energia del Sole è generato da una sequenza di reazioni nucleari detta catena protone-protone. Ecco i due passi della sequenza:
|
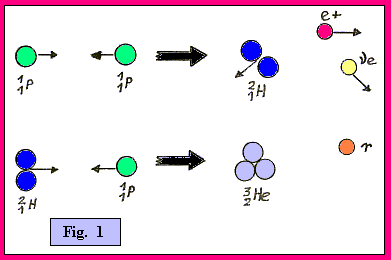 |
|
ELEMENTARI NOZIONI SULLE REAZIONI NUCLEARI Diamo alcune elementari nozioni sulle reazioni nucleari, per spiegare quanto detto nel paragrafo precedente. Quando si dà il simbolo di un elemento, lo si accompagna con due dati relativi al suo nucleo, secondo la notazione: SimboloAZ, dove:
Un'altra nozione che è opportuno dare è quella di particelle isotopi di uno stesso elemento: sono particelle tutte indicative dello stesso elemento, perchè aventi tutte lo stesso numero atomico (e quindi lo stesso numero di elettroni, e quindi le stesse proprietà chimiche). Ad esempio, sono isotopi dell'idrogeno: (1) l'idrogeno "normale", H11, (nucleo composto di un solo protone), (2) il deuterio, detto anche idrogeno pesante, H21, (un protone e un neutrone), (3) il trizio, H31, (un protone e due neutroni). La forza che costringe i nucleoni (protoni, neutroni) a rimanere coesi in un nucleo è la forza nucleare. E' estremamente intensa se i nucleoni sono a distanze molto piccole, ma diminuisce rapidamente se i nucleoni si trovano a distanza sensibilmente maggiore. Precisiamo meglio: due protoni che si trovino a una distanza compresa tra 0.5•10-15 m e 3•10-15 m si attraggono con una forza nucleare maggiore della forza coulombiana (elettrica) con cui si respingono, e quindi restano coesi. Se invece, vincendo la forza nucleare, vengono allontanati a distanza maggiore di quella sopra indicata, allora la forza coulombiana di repulsione ha il sopravvento sulla nucleare, e i due protoni si allontanano ulteriormente. Stabilito quanto sopra, quando protoni e neutroni sono legati in un nucleo, questo ha una massa minore rispetto alla somma delle masse dei componenti. Per esempio, il nucleo del deuterio (un protone + un neutrone) ha una massa di 3.3434•10-27 Kg, mentre la somma delle masse dei due nucleoni è: mp + mn = (1.725•10-27 + 1.748•10-27) Kg = 3.3473•10-27 Kg. Quei 0.039•10-27 Kg che sono scomparsi, (massa mancante, difetto di massa) dove sono andati a finire? Risposta: si sono trasformati in energia. Ogni volta che si forma un nucleo di deuterio, il difetto di massa del nucleo corrisponde all'energia che si rende disponibile nell'ambiente. E questo vale in tutte le reazioni di fusione nucleare, e quindi anche in quella descritta sopra che ha luogo nel nucleo del Sole. Questa energia sarà: E = m • c2 = 0.0039•10-27 • (3•108)2 = 3.51•10-13 joule = 2.2 MeV (mega elettronvolt), una notevole quantità di energia. E' importante che il lettore comprenda che questa energia viene conferita al fotone gamma che viene prodotto al termine della reazione nucleare detta di catena protone-protone, descritta sopra. Quindi, nell'interno del Sole l’idrogeno ha la funzione di carburante nucleare, mentre l’elio e gli elementi più pesanti (prodotti in altre reazioni di fusione) rappresentano la “cenere" che si ritrova alla fine del ciclo di produzione di energia. La massa attuale del Sole è composta per il 71% di idrogeno e per il 27% da elio, mentre i nuclei più pesanti non arrivano al 2%. Con il passare del tempo, la quantità di idrogeno nel Sole è destinata a diminuire mentre, di pari passo, deve aumentare quella di elio e dei nuclei più pesanti. E’ importante notare che la reazione di fusione nel Sole avviene con un consumo molto piccolo di idrogeno, e ciò spiega come mai il Sole riesce a produrre energia da miliardi di anni. |
|
STRUTTURA INTERNA DEL SOLE L’energia prodotta nel nucleo del Sole inizia così il suo cammino verso l’esterno, trasportata dai fotoni gamma. Nel corso di questo cammino, il fotone diminuisce progressivamente la propria frequenza fino a che questa giunge nell’ambito delle frequenze visibili. Dalla figura 2, si vede che il nucleo fa parte della zona radiativa, in cui temperatura e densità sono tali da permettere propagazione di energia per radiazione. L’ultimo quarto del raggio solare costituisce la zona convettiva (l'energia vi si trasmette per convezione). La “superficie” del Sole è detta fotosfera, un guscio di 600 Km di spessore, con temperatura di circa 6000 K. Tra i fenomeni che hanno luogo nella fotosfera c’è quello delle macchie solari, zone che appaiono scure perché si trovano a temperatura di 1000-1500 K minori di quelle delle zone circostanti. Hanno un periodo di manifestazione abbondante ciclico, di circa 11.2 anni. Al di sopra della fotosfera si trova l’atmosfera solare, divisa in cromosfera e corona. Le condizioni più favorevoli per studiare l’atmosfera solare si hanno durante le eclissi totali di Sole. Durante esse la cromosfera appare come un anello di colore rosso. Ha uno spessore di circa 6000 Km. La corona appare invece come un alone bianco che si estende all’esterno della cromosfera per diversi raggi solari. |
 | |
|
MASSA SOLARE CONSUMATA IN UN ANNO Calcoliamo la massa di Sole che si disperde ogni anno nello spazio a causa della sua emissione energetica, a partire da questo dato appreso dalla termologia: su una superficie di 1 m2, perpendicolare ai raggi solari e posta al di fuori dell’atmosfera terrestre, arriva ogni secondo un’energia di 1.35•103 watt. Cominciamo col calcolare l’energia totale E, emessa dal Sole in un anno, che arriva su una superficie sferica ideale avente centro nel centro del Sole e raggio 1 AU, (astronomic unit, 1.5•1011 metri): E = 1.35 • 103 W/m2 • 4•p • (1.5•1011 m)2 • (365•24•3.6•103 s) = 1.2 • 1034 joule Calcoliamo ora il valore assoluto della variazione della massa solare, Dm, dovuta all'emissione di energia, mediante la formula: Dm = E / c2 Dm = (1.2 • 1034) J / (3 • 108 m/s)2 = 1.34 • 1017 Kg cioè, il Sole perde ogni anno una massa di 134.000 miliardi di tonnellate. Si tratta di una frazione infinitesima della sua massa. |
|
EVOLUZIONE STELLARE Luminosità assoluta L0 di una stella è la potenza totale che essa irraggia. Il colore di una stella è funzione della sua temperatura superficiale Ts. Negli anni Venti gli astronomi E. Hertzsprung (danese, 1873 - 1967) e H. Russel (americano, 1877 - 1957) ebbero l’idea, l’uno indipendentemente dall’altro, di rappresentare le stelle in un unico diagramma (poi detto diagramma H-R), in cui ogni stella è posizionata in un punto che ha per ascissa il logaritmo della sua temperatura superficiale e per ordinata il logaritmo della sua luminosità assoluta (temperatura crescente verso sinistra e luminosità crescente verso l’alto). I punti rappresentativi delle stelle osservate si addensano in quattro zone :
|
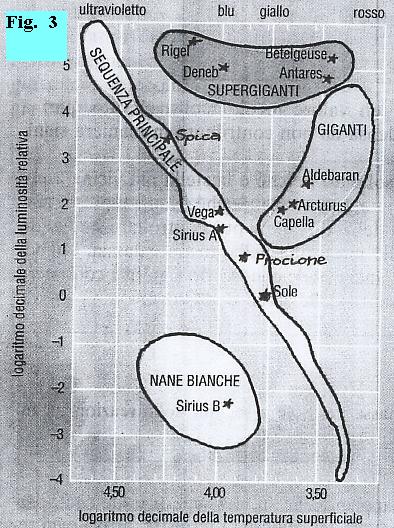 |
| Al momento della nascita, il punto rappresentativo di una stella sul diagramma H-R è posizionato tra la sequenza principale, la zona delle giganti e la zona delle supergiganti. Con il passare del tempo, l’evoluzione della stella è tale che il punto rappresentativo si sposta all'incirca verticalmente verso il basso (la luminosità decresce mentre la temperatura rimane pressochè costante). Poi l’evoluzione è tale che il punto rappresentativo si sposta più o meno orizzontalmente (luminosità costante e temperatura che cresce) fino a raggiungere la sequenza principale. Il punto rappresentativo della stella permane nella sequenza principale per circa il 70% della vita della stella (attuale situazione del Sole) fino a quando il combustibile nucleare (idrogeno) incomincia a scarseggiare. A questo punto, a seconda della massa della stella, sono possibili tre tipi di evoluzione. |
|
FASE FINALE DELL’EVOLUZIONE STELLARE Scarseggiando il combustibile nucleare, la forza di gravità che tende a far implodere la stella verso l’interno (collasso gravitazionale), non è più bilanciata dalla pressione energetica verso l’esterno prodotta dalle reazioni nucleari. La fase finale dell'evoluzione di una stella è dunque dipendente dal contrasto tra queste due forze e la modalità secondo la quale essa si svilupperà dipende dalla massa della stella:
|
|
MECCANICA NEWTONIANA E MOTI PLANETARI Mercurio, Venere, Marte e la stessa Terra sono detti pianeti terrestri, perché hanno dimensioni e densità paragonabili a quelle della Terra. Giove, Saturno, Urano e Nettuno sono detti pianeti giganti perché hanno dimensioni decisamente maggiori ma densità altrettanto decisamente minore (non hanno una "crosta" solida simile a quella terrestre). Il grande merito della meccanica newtoniana fu quello di aver finalmente dato una spiegazione teorica soddisfacente dei moti del sistema solare. Newton pervenne a questo risultato enunciando (1) le tre leggi della dinamica e (2) la legge della gravitazione universale: F = G • m1•m2 / r2 (4), essendo G la costante gravitazionale di Newton che vale 6.67•10-11 N•m2•Kg-2 E' importante che il lettore comprenda che utilizzando le leggi sopra dette, gli studiosi sono in grado di risolvere (con un accettabile grado di precisione) non solo tutti i problemi relativi ai posizionamenti planetari ma anche quelli relativi alle interazioni planetarie. Infatti, un vero trionfo della meccanica newtoniana si ebbe nel secolo XIX quando due matematici (J. Adams e U. Le Verrier) furono in grado di calcolare (l'uno indipendentemente dall'altro) la posizione di un nuovo pianeta (Nettuno), dalle perturbazioni riscontrate in Urano, appunto applicando le leggi di Newton. La posizione venne indicata da Le Verrier con successo all'astronomo J. Galle, nel 1846. Alla fine del secolo XIX però gli astronomi si trovarono di fronte ad un problema la cui soluzione non fu possibile ricorrendo alla meccanica newtoniana. Abbiamo visto infatti nel capitolo dedicato alla meccanica celeste che le linee degli apsidi delle orbite planetarie ruotano in senso diretto. Ebbene, per Mercurio, gli astronomi trovarono che c'era una discrepanza sensibile tra il valore annuo di rotazione della sua linea degli apsidi così come risultava dalle osservazioni, e il valore che risultava dal calcolo teorico secondo la meccanica newtoniana. Quest'ultima quindi manifestava per la prima volta una imperfezione. Dopo il 1916 invece si poté constatare che la teoria della relatività generale forniva un valore annuo della rotazione dell'asse afelio - perielio di Mercurio che coincideva con quello delle osservazioni. |
|
LA FASCIA DEGLI ASTEROIDI Tra gli oggetti che popolano il sistema solare vi sono anche:
La scoperta degli asteroidi fu facilitata dalla legge di Titius-Bode (due astronomi tedeschi). Si tratta di una relazione empirica data dalla formula: dn = (D / 3) • (2n-2 + 1), dove D è la distanza media Terra-Sole, che vale circa 1.5•1011 m, ed è detta unità astronomica (UA). Questa legge fornisce, con buona approssimazione, le distanze medie dn tra il Sole e i primi sette pianeti. Per n = 1 si ha la distanza di Mercurio, per n = 2 Venere, per n = 3 si ha dn = D, ovviamente la distanza Terra-Sole. Per n = 4, 6, 7 e 8, la formula permette di trovare le distanze rispettivamente di Marte, Giove, Saturno e Urano. Però, per n = 5 non si ha nessun pianeta. Proprio cercando nella zona di cielo relativa a questo “posto libero” il Piazzi scoprì il primo asteroide. Per molto tempo si credette che gli asteroidi fossero i resti di un pianeta, posto tra Marte e Giove, frantumato dall’azione gravitazionale di quest’ultimo. Oggi, la maggior parte degli astronomi ritiene che proprio la presenza del “gigante” Giove abbia impedito a tale ipotetico pianeta di formarsi. Secondo tale schema di pensiero, gli asteroidi non sarebbero altro che “materiale da costruzione” di un nuovo pianeta. |
|
LE COMETE Questi corpi hanno orbite caratterizzate da una fortissima eccentricità: al perielio si avvicinano molto al Sole, mentre l’afelio può essere molto più lontano dell’orbita di Plutone. Esiste una “riserva” di comete in una zona detta nube di Oort, posta a una distanza dal Sole compresa tra le 30.000 UA e le 50.000 UA. Le comete sono formate essenzialmente di ghiaccio e polveri. Per questa ragione sono spesso descritte come “palle di neve sporca”. Il loro studio è molto interessante proprio per la presenza delle polveri che si ritiene siano campioni della composizione del sistema solare all’epoca della sua formazione. Per la maggior parte del suo percorso una cometa è a noi invisibile. Soltanto quando si avvicina alla Terra, investita dalla radiazione solare, diviene abbastanza splendente da essere talvolta visibile anche ad occhio nudo. In tali condizioni essa risulta composta dalle seguenti parti:
|
|
LA FORMAZIONE DEL SISTEMA SOLARE I. Kant nel 1755, e P.S. de Laplace nel 1796, avevano proposto che il sistema solare avesse tratto origine da una nebulosa primordiale, cioè da una nube di gas e particelle in rotazione. La concentrazione della parte centrale della nebulosa avrebbe prodotto il Sole. A differenti distanze dal Sole si sarebbero avute concentrazioni di materia che avrebbero dato luogo ai pianeti. Il tutto causato dalla combinazione della gravità e del moto rotatorio della materia. Ci sono diverse ragioni che sostengono una tale ipotesi. La più notevole è che praticamente tutti i corpi del sistema solare orbitano nello stesso senso, nell'ambito di una fascia ampia meno di una decina di gradi. Altra ragione è che i moti di rotazione dei pianeti hanno tutti lo stesso senso dei moti di rivoluzione (tranne Urano). Sono stati eseguiti al computer dei modelli matematici di formazione del sistema solare, e da essi si è tratta una sorprendente analogia con la realtà. Oggi sappiamo che l'inizio della formazione del Sole avvenne circa 4.5 miliardi di anni fa. Il progressivo collasso di materia verso il centro ha fatto raggiungere al nucleo le condizioni di pressione e temperatura che hanno innescato il processo di fusione nucleare. All'incirca tra 5 miliardi di anni il Sole diverrà una supergigante rossa. A quel punto esso ingloberà le orbite di Mercurio, di Venere, della Terra e forse anche di Marte. |
|
LE GALASSIE Il primo a rendersi conto, osservandola tramite un cannocchiale, che la Via Lattea era costituita da un insieme sterminato di stelle, fu Galileo, nel 1610. Oggi sappiamo che la Via Lattea è una galassia. Essa è anche detta Galassia. Gli astronomi hanno stabilito che la distribuzione stellare ha una struttura gerarchica. Il primo raggruppamento di stelle è detto ammasso stellare (un esempio di ammasso stellare è quello delle Pleiadi). Una galassia è invece un insieme di ammassi stellari, tenuti insieme dalla forza di gravità. Il sistema solare fa parte di una galassia a spirale, la Via Lattea o Galassia, che ha la forma di un discoide schiacciato, del diametro di circa 100 miliardi di anni-luce, un'altezza di circa 13 miliardi di anni-luce, e che contiene circa 200 miliardi di stelle. La struttura gerarchicamente superiore alle galassie è quella dei raggruppamenti o ammassi di galassie. Un esempio di ammasso di galassie è quello detto Gruppo locale, costituito da una trentina di galassie, tra le quali sono notevoli la Via Lattea, la Grande e la Piccola Nube di Magellano e la galassia di Andromeda (quest'ultima anch'essa una galassia spirale, come la Via Lattea). Continuando nella struttura gerarchica, gli ammassi di galassie spesso sono riuniti in diversi ammassi, per dar luogo a un superammasso. Per gli astronomi i superammassi di galassie sono strutture molto importanti e interessanti perchè sono considerati delle specie di “universi in miniatura” o modelli in scala dell’intero universo. Studiando la dinamica e l'evoluzione di un superammasso si possono compiere progressi nelle conoscenze della evoluzione dell'intero universo. |
|
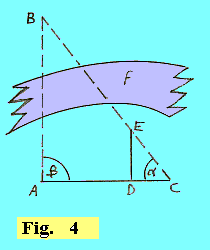
LA MISURA DI DISTANZE ASTRONOMICHE Oggi, tramite radar astronomici, è possibile misurare la distanza Terra-Luna con la precisione di qualche centimetro. Per misurare distanze grandi ma non enormi si usa il metodo della triangolazione, così chiamato perché basato sulla geometria del triangolo. la figura 4 mostra uno dei modi che può usare un osservatore posto in A per misurare, per triangolazione, la distanza, per esempio, di un campanile, posto in B, al di là del fiume f. |
 |
|
La base, AC, misurata con precisione, viene presa perpendicolare alla direzione della distanza AB. Il triangolo BAC è simile a un qualsiasi altro triangolo, per esempio EDC, che sia rettangolo in D, e che abbia lo stesso angolo a in C. Dalla similitudine dei due triangoli si ricava: AB/AC = DE/DC, da cui si deduce AB = AC•DE/CD, dove i tre segmenti che figurano al secondo membro possono essere tutti misurati agevolmente. In generale, per eseguire una triangolazione è sempre necessario fissare una base, cioè un lungo segmento AC, di lunghezza nota, e misurare gli angoli a e b. Anche per la misura delle distanze astronomiche si fa uso della triangolazione. Con questo metodo, maggiore è la distanza che si deve misurare, e più lungo deve essere il segmento che si fissa come base. Con una base lunga 250 metri si può misurare una distanza di 3 o 4 chilometri ma, evidentemente, una tale base è troppo corta per misurare, ad esempio, la distanza alla quale si trova la Luna. |
| La misura di questa distanza che fu eseguita per la prima volta nel 1751, si fa prendendo come estremi due lontanissime località, M e N, poste sullo stesso meridiano . Si è così trovato che il centro della Luna dista dal centro della Terra 384403 Km. basato essenzialmente su una triangolazione è anche il metodo per trovare la distanza Terra-Sole. Si è trovato che essa ha il valore medio di 149.599.000 Km, cioè 1.5•1011 m, distanza alla quale è stato dato il nome di unità astronomica (UA). | 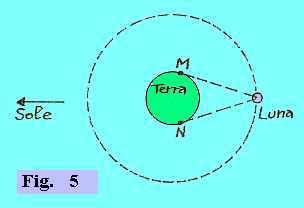 |
| IL METODO DELLA PARALLASSE | |
| Il metodo della parallasse è sostanzialmente analogo a quello della triangolazione. Anch'esso necessita di una base. E' stato ideato per misurare le distanze che ci separano da un certo numero di stelle. Evidentemente, trattandosi di distanze stellari, si deve ricorrere a una distanza lunghissima, talmente lunga da non essere contenuta sulla piccola Terra. | 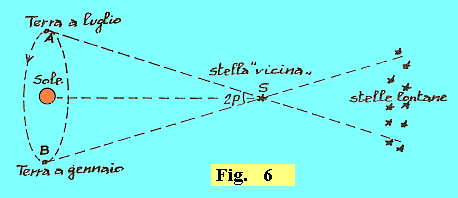 |
|
Si tratta dell'asse maggiore dell'orbita terrestre. Come risulta dalla figura 6, cambiando durante un anno la direzione secondo cui osserviamo una stella S, questa sembra descrivere, sullo sfondo del cielo stellato composto delle altre stelle molto più lontane, un piccolissimo ellisse (le stelle dello sfondo, invece, ci appaiono praticamente fisse, essendo impercettibile la loro ellisse apparente). Allora, la distanza Sole - stella S può essere determinata conoscendo la distanza AB = 2• AU e misurando l'angolo 2•p. L'angolo p, angolo sotto il quale dalla stella S è visto il semiasse maggiore dell'orbita terrestre, è detto parallasse annua della stella S. Le parallassi delle stelle sono piccolissime. Nessuna parallasse raggiunge il secondo di arco. Grazie al satellite astronomico Hipparcos, un satellite dell’Agenzia Spaziale Europea che è rimasto in orbita attorno alla Terra dal 1989 al 1993, sono state determinate le parallassi di circa 120.000 stelle, che sono quelle a noi più vicine. la più vicina, di nome Proxima centauri (si trova nella costellazione del Centauro), ha una parallasse di 0.782 secondi di arco. Si trova alla distanza di circa 40.000 miliardi di chilometri. Per le distanze di ordine stellare è stata definita una speciale unità di misura: il parsec che è la distanza alla quale si dovrebbe trovare una stella per avere la parallasse di un secondo di arco. Si indica con il simbolo pc. Si ha: 1 pc = 2.063•105 UA = 3.09•1013 Km = 3.26 anni-luce. Avendo detto che la parallasse di Proxima Centauri è p = 0".762, indicando con d0.762 la distanza corrispondente a questa parallasse, ed avendosi proporzionalità indiretta tra parallasse e corrispondente distanza, possiamo dire che: d0.762/1 pc = 1"/0".762, da cui d0.762 = (1/0.762) pc = 1.31 pc = 4.05•1013 Km, cioè Proxima Centauri dista da noi circa quattro anni-luce. Da quanto detto, dunque, se p è la parallasse di una stella, in secondi di arco, 1/p sarà la distanza della stella in parsec. |
|
ALTRI METODI PER MISURE DI DISTANZE ASTRONOMICHE Il metodo della parallasse non è applicabile alla misura delle distanze di galassie, perché sono tutte troppo lontane. Si fa uso delle proprietà di una famiglia di stelle pulsanti dette Cefeidi. La luminosità delle stelle di questa famiglia varia periodicamente nel tempo e il periodo di questa variazione di luminosità è legato alla potenza media irraggiata (energia luminosa irraggiata ad ogni secondo), secondo una ben precisa legge. Allora, si sfrutta la proprietà anzidetta secondo questa procedura: (1) Si misura accuratamente la durata di una oscillazione luminosa di una cefeide, (2) Dal periodo si ottiene la luminosità intrinseca della cefeide, applicando la legge di cui si è parlato. (3) Si misura quindi facilmente la luminosità apparente della cefeide. (4) Dal confronto tra le due luminosità si ottiene la distanza della stella, tenendo presente che essa varia in ragione inversa del quadrato della distanza stessa. Utilizzando questo metodo, si sono misurate distanze da galassie che distano fino a 10 milioni di parsec, cioè 10 Mpc. Per galassie più lontane si ricorre a un’altra proprietà che lega la luminosità assoluta di una galassia (cioè l’energia luminosa emessa ad ogni secondo) a una proprietà misurabile dalla Terra. In questo caso si tratta della velocità di rotazione della galassia, che con i potenti telescopi moderni si riesce a misurare fino a distanze di qualche centinaio di megaparsec. |
|
DIVERSE MODALITA' DI OSSERVAZIONE Per la maggior parte della sua storia l’umanità ha osservato il cielo soltanto nella banda della luce visibile, sia ad occhio nudo sia con l’uso di telescopi. Certamente questa tecnica di osservazione ha avuto enormi meriti e ha permesso, tra l’altro, la nascita stessa dell’astronomia e dell’astrofisica. Ma nei corpi celesti avvengono fenomeni dei quali la luce visibile non può darci alcuna testimonianza. Per questo, nel corso del ventesimo secolo si sono sviluppate tecniche osservative che permettono di scrutare il cielo in altro modo che non sia quello di utilizzare lo spettro della luce visibile:
La tecnologia dei satelliti artificiali permette di aprire nuove possibilità anche nella tecnica osservativa più antica, quella nella gamma dei raggi visibili. Infatti, il telescopio Hubble, lanciato nel 1990, e riparato in orbita nel 1993, dopo che si era reso evidente un difetto del suo specchio di 2.4 m di diametro, non risente delle turbolenze atmosferiche e permette di ottenere immagini che sarebbe ben difficile ottenere da terra. |