(13)

dove D q = k_p V_m detta deviazione di fase, indica il valore massimo della variazione di fase introdotta dalla modulazione.

Supponendo nulla q = 0 l'espressione del segnale modulato è

v(t) = Acos j (t)=A cos(w _c t+ q )= Acos(w _C t+D q cos w _m t)

(14)

Dalla relazione 14 si possono ricavare la pulsazione e la frequenza istantanea del segnale PM

w = dj /dt=w _C -D q _{w m}sen w _m t da cui f=f_C-D q f_msen w _m t

(15)

Si noti l'analogia fra l'espressione di f nella 15 e nella 7. Il fattore Dq f_m rappresenta la massima deviazione di frequenza (qui dipendente anche da f_m) che subisce la portante quando viene modulata in fase; questo fattore può dunque essere assimilato alla deviazione di frequenza D _f.

È interessante analizzare il legame tra la FM e la PM:

l’angolo istantaneo di fase per una PM vale

j (t)=w _C+k_p v_m (t)

(16)

per la modulazione di frequenza l’angolo di fase vale

j (t)=w _C+k_{f ò 0} ^t v_m (t) dt

(17)

confrontando la 16 con la 17 si deduce che un segnale modulato in frequenza si può ottenere da un modulatore di fase avente la modulante integrata; viceversa un segnale modulato in fase si può ottenere da un modulatore di frequenza derivando la modulante.

Nella figura 1 vengono sintetizzati tramite schemi a blocchi i concetti ora esposti.

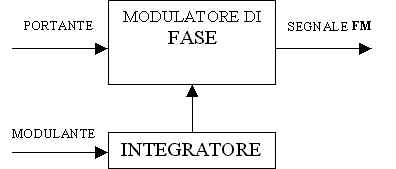
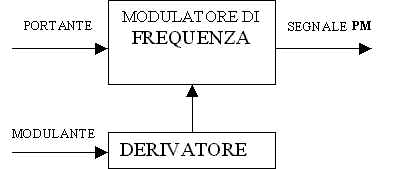
Fig. 1 a) Segnale FM ottenuto da un modulatore di fase; b)Segnale PM ottenuto da un modulatore di frequenza.