Struttura
La struttura di una fibra ottica di tale tipo è indicata nella fig. 5:
Profilo d'indice(si definisce profilo d'indice, l'andamento dell'indice di rifrazione al variare della distanza dal centro della fibra verso la periferia)
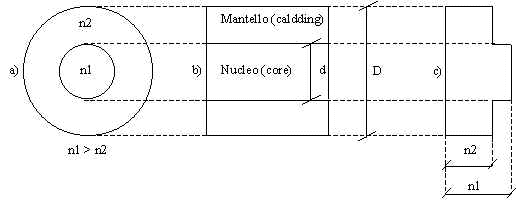
Fig. 5 Fibra ottica step index a) sezione trasversale b) sezione longitudinale c) profilo d'indice
Nella figura si osserva una struttura coassiale di due materiali dielettrici trasparenti. La regione più interna è un nucleo cilindrico sottile (in inglese core) avente un indice di rifrazione n1; il nucleo è circondato da un mantello (in inglese cladding) avente un indice di rifrazione n2 minore di n1.
All'esterno del cladding ci sono ancora due ulteriori strati, non indicati in figura che hanno essenzialmente funzioni di protezione e di irrobustimento.
Le dimensioni della fibra ottica sono mediamente le seguenti:
Il materiale base è la silice, sia per le buone proprietà meccaniche che persistono anche se il materiale è ridotto in fili molto sottili, sia per l'ottima trasparenza nello spettro visibile e nell'infrarosso. Per aumentare l'indice di rifrazione n1 del core si aggiungono impurità di ossido di fosforo; per diminuire l'indice di rifrazione n2 del cladding si aggiungono invece impurità di ossido di fluoro. Attualmente sono sul mercato anche fibre di plastica meno costose delle precedenti ma di prestazioni inferiori.
Dall'esame della fig. 5c si osserva che l'indice di rifrazione rimane costante all'interno sia del nucleo che del mantello e subisce una brusca variazione a gradino (da cui il nome) dal valore n1 al valore n2 passando dal nucleo al mantello.
Propagazione
Si vuole esaminare la propagazione della radiazione luminosa applicando le leggi di rifrazione e riflessione dell'ottica geometrica.
Si ha riflessione totale quando il raggio luminoso incide la superficie di separazione core cladding con un angolo di incidenza, a , maggiore dell'angolo limite, a 1L (fig. 6); il raggio viene pertanto intrappolato completamente nel core ed in esso si propaga per effetto di riflessioni successive. Un raggio che si propaga con queste modalità, si definisce raggio guidato e la propagazione si definisce propagazione guidata.
Viceversa se il raggio di luce incide la superficie di separazione core cladding con un angolo di incidenza minore dell'angolo limite, si ha riflessione nel core e rifrazione nel cladding.
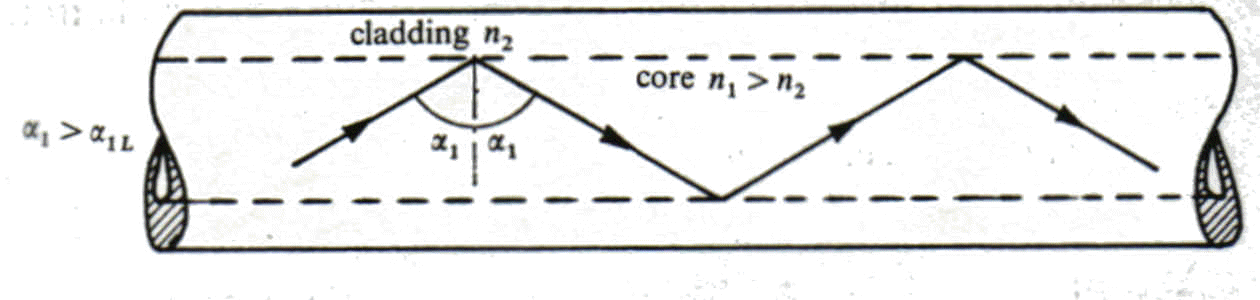
Fig. 6 Propagazione guidata nelle fibre ottiche step index

Fig. 7 Accoppiamento sorgente luminosa fibra ottica
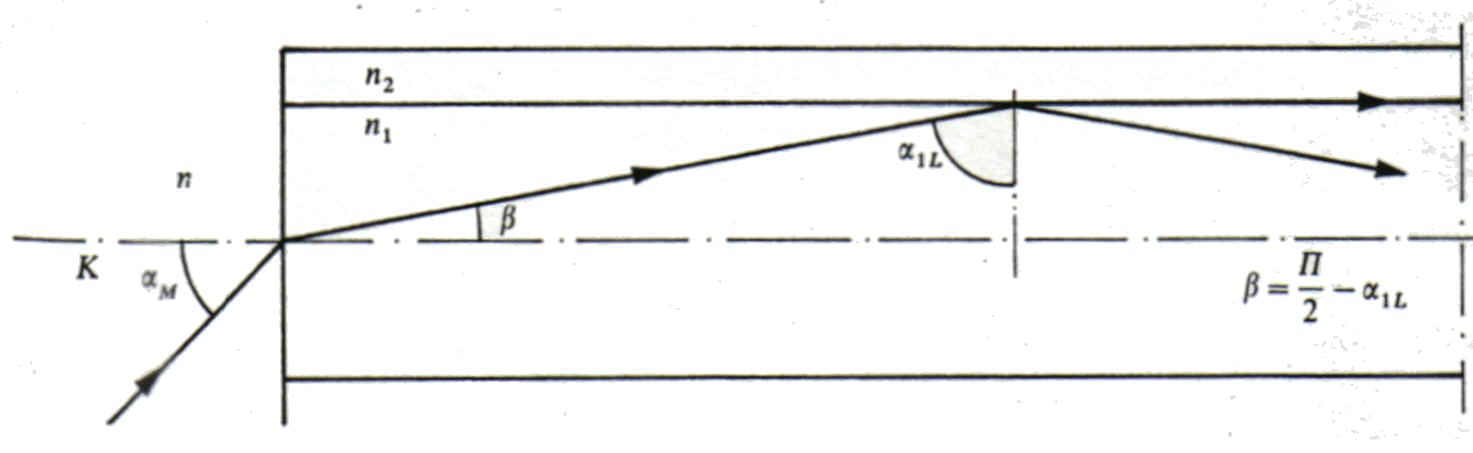
Fig. 8 angolo di accettazione ed angolo limite in una fibra ottica
L'energia connessa al raggio rifratto è perduta agli effetti della trasmissione; tale fenomeno ripentendosi ad ogni incidenza provoca, dopo poche riflessioni, la perdita totale della trasmissione.
Un raggio che si propaga con questa modalità, si definisce raggio irradiato.
Si prenda ora in esame l'accoppiamento sorgente fibra, cioè l'ingresso in fibra dei raggi luminosi prodotti da una sorgente luminosa esterna alla fibra, vedi fig. 7.
A tale riguardo si può definire una efficienza di accoppiamento:
h a=Pi/Ps
(5)
dove: Ps è la potenza emessa dalla sorgente; Pi è la potenza immessa e guidata nella fibra. Questa efficienza è legata a vari fattori: tipo di sorgente optoelettronica, rapporto fra superfici della sorgente e della fibra, profilo d'indice di rifrazione ed apertura numerica.
È importante determinare la condizione ottimale di accoppiamento sorgente fibra che permette la propagazione guidata dentro la fibra ottica dei raggi entranti in essa tale scopo si definiscono l'apertura numerica, NA (Numerical Aperture), e l'angolo di accettazione a M, che sono legati dalla relazione:
NA = n sen a M
(6)
dove n è l'indice di rifrazione del mezzo in cui avviene l'accoppiamento sorgente fibra; se tale mezzo è l'aria n ~ n0 = 1.
Osservando la fig. 8 si definisce angolo di accettazione, a M l'angolo che il raggio entrante forma con l'asse della fibra se, tale raggio se entrato nel core, incide sulla superficie di separazione con il cladding con un angolo pari a quello limite a L si ha propagazione guidata.
Si può quindi concludere che i raggi entranti in fibra e compresi in un cono d'angolo al vertice 2a M sono raggi guidati in quanto incidono sulla superficie di separazione core cladding con angoli maggiori od eguali all'angolo limite a L Tale cono si definisce cono di accettazione.
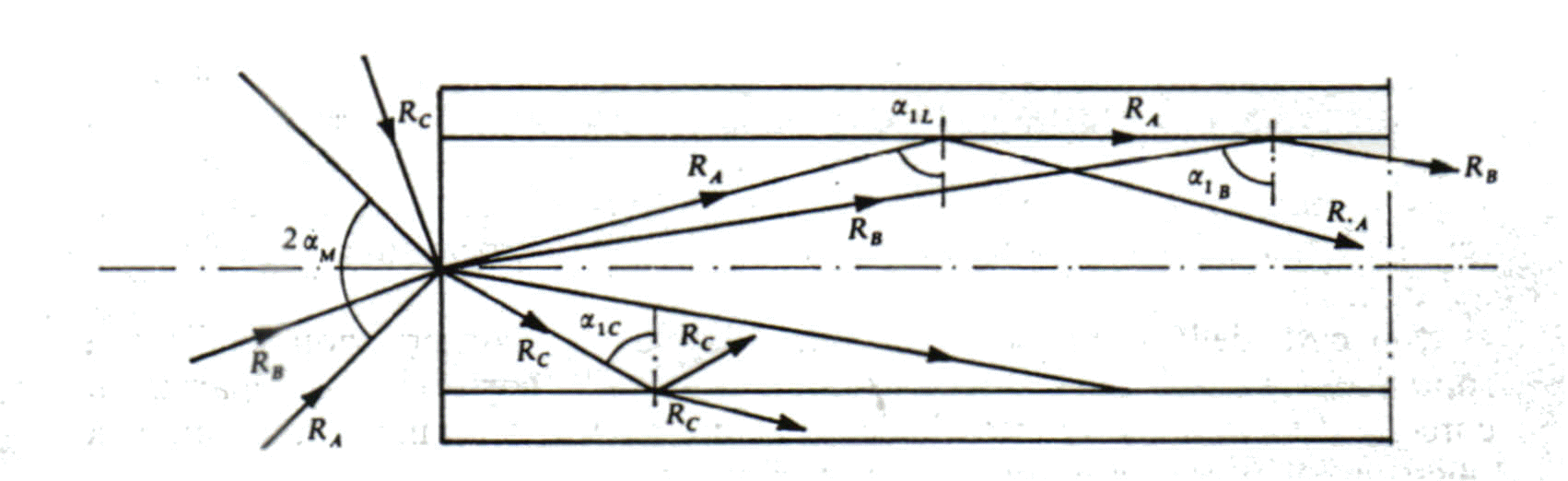
Fig. 9 Propagazione della radiazione nella fibra ottica
Invece i raggi che entrano in fibra e sono esterni al cono di accettazione sono del tipo irradiato, in quanto incidono la superficie di separazione core cladding con angolo minore dell'angolo limite; quanto sopra affermato si può osservare nella fig. 9.
In essa:
Esiste una relazione fra l'apertura numerica e gli indici di rifrazione della fibra
NA=Ö (n12- n22)
(7)
Infatti applicando la legge di Snell alla superficie di separazione aria core si ha, osservando la fig. 3.6:
NA = nsena M = n1 senb = n1 sen[(p /2)- a 1L]= n1cosa 1L
(8)
per l'aria, essendo n ~ n0 = 1 la relazione precedente può essere scritta:
NA = nsena M = n1 Ö (1- sen2a 1L)= n1 Ö (1- n22 /n12-)= Ö (n12- n22)
(9)
ordine di grandezza di NA: da 0,15 a 0,25 e quindi angoli al vertice del cono di accettazione 2a M compresi fra 17,2° e 28,9°.
L'angolo di accettazione e la corrispondente apertura numerica presentano quindi valori molto bassi che se da un lato riducono l'efficienza di accoppiamento dall'altra riducono un fenomeno da evitare: quello della dispersione.
Si potrebbe credere che la propagazione in fibra ottica possa avvenire per tutti i raggi guidati. In realtà non è cosi. Solo alcuni di essi riescono a propagarsi.
Infatti perché un raggio guidato si propaghi in tutta la lunghezza della fibra è necessario, vedi fig. 3.8, che dopo ogni riflessione si abbia uno sfasamento di 180° e quindi che dopo due riflessioni successive, il campo E.M. nel punto B abbia la stessa fase che aveva nel punto A; in tal modo il raggio che parte da B è nelle stesse condizioni di quello che è partito da A. Tale conservazione di fase dipende dall'apertura numerica, NA, dal diametro del core, d, (e quindi dalla lunghezza dei percorsi dei raggi riflessi) e dalla lunghezza d'onda, l , della radiazione entrante in fibra.
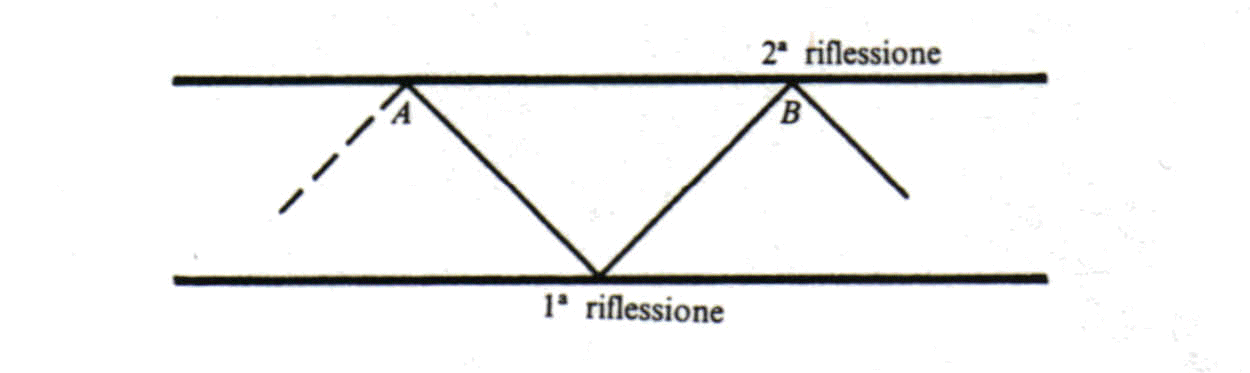
Fig. 10 Propagazione di raggio guidato entro il core
Il fatto che soltanto alcuni raggi guidati possono propagarsi si può spiegare in maniera semplificata ricordando quanto succede nelle linee di trasmissione chiuse in corto circuito. In tali linee si ha la riflessione totale poiché la tensione subisce una rotazione di fase di 180°; per una impedenza di carico diversa da zero si ha una riflessione soltanto parziale con assorbimento di energia da parte del carico.
Nel caso della fibra, se non viene rispettata la conservazione della fase sopraddetta, non si ha più riflessione totale sulla superficie di separazione core cladding ma una parte dell'energia passa nel cladding. Dopo qualche riflessione il raggio si esaurisce e non si ha più propagazione.
Riepilogando: l'energia luminosa si propaga secondo un numero discreto di "modi di propagazione". La direzione in cui viaggia il modo di propagazione, in ottica geometrica si definisce raggio.
Il numero dei modi possibili di propagazione di una radiazione luminosa di lunghezza d'onda;l , in una fibra ottica con un core di diametro "d" ed apertura numerica "NA" è definito approssimativamente dalla seguente relazione:
P ~ 0,5 (p dNA/l )2
(10)
Dispersione
Nelle fibre ottiche esiste il fenomeno della dispersione che provoca un allargamento temporale dell'impulso che si propaga dentro la fibra.
Si hanno due tipi di dispersione: dispersione modale e dispersione cromatica.
Si esamina ora la dispersione modale. Da quanto sopraddetto e dall'esame delle figure 7 e 9 si rileva che l'energia emessa da una sorgente impulsiva luminosa ed entrante in fibra con angolazioni diverse si propaga al suo internò con un numero discreto di modi di propagazione cioè percorrendo un numero discreto di traiettorie differenti, tutte con la stessa velocità u, in quanto l'indice di rifrazione, n1, è costante in tutto il core. I tempi di arrivo saranno quindi necessariamente diversi, si veda la fig. 11. Di conseguenza la durata, t , dell'impulso d'ingresso aumenterà in uscita al valore t ’.
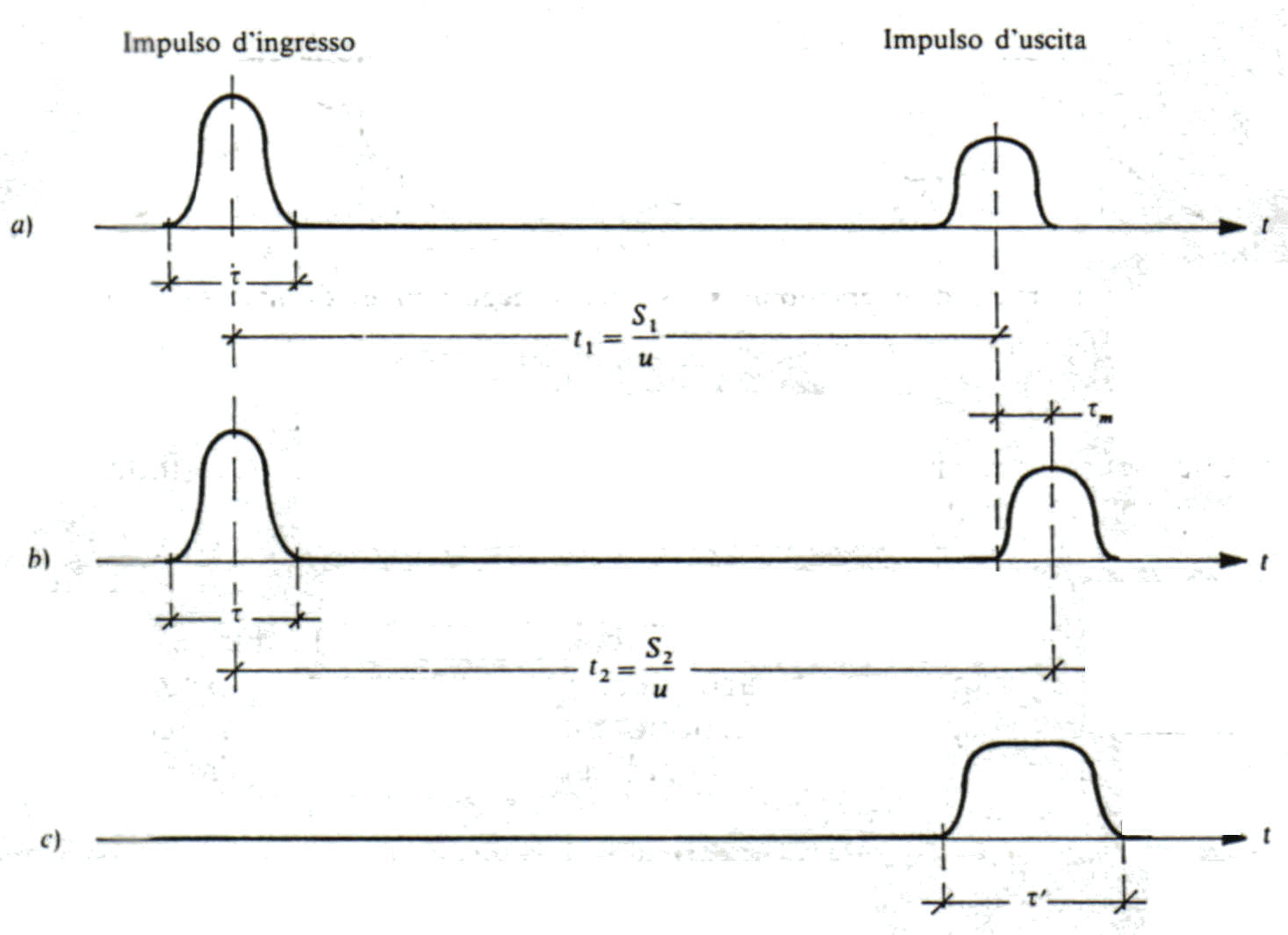
Fig. 11 Allungamento nel tempo dell'impulso d'ingresso dovuto alla dispersione modale a)t1: tempo impiegato dall'impulso luminoso a percorrere la traiettoria più breve b)t2 :tempo impiegato dall'impulso luminoso a percorrere la traiettoria più lunga c) impulso luminoso risultante d'uscita
Dalle 6 e l0 si ricava che se l'apertura numerica NA ha valori bassi, è anche basso il numero dei modi di propagazione, l'angolo di accettazione e quindi la dispersione modale.
Il valore della dispersione modale, t m, Si esprime in ns/km ed è legato alle caratteristiche della fibra dalla relazione:
t m=(n1/c)(n1-n2/n2)
(11)
Infatti il raggio che si propaga lungo l'asse della fibra ottica di lunghezza L è quello che compie il percorso più breve nel tempo
t1=L/u1=Ln1/c
Il raggio che incide sulla superficie di separazione core-cladding con l'angolo di incidenza a lL (è il raggio RA della fig. 9) è quello che compie il percorso lungo nel tempo: t2=(L/sena 1L)(n1/c)
Facendo la differenza di questi due tempi e ricordando la relazione 4 si ottiene, per una fibra di lunghezza unitaria, la relazione 11. Infatti
t m=t2-t1/l=(n1/c) (1/sena 1L-1)= (n1/c) (n1/n2-1)
L'ordine di grandezza di t m per questo tipo di fibra è 10¸ 70 ns/km.
L'allungamento nel tempo dell'impulso dovuto alla dispersione modale è un notevole inconveniente nel caso di trasmissione di tipo numerico. Infatti se gli impulsi si allargano troppo si possono sovrapporre gli uni agli altri con conseguente impossibilità di ricezione. Questo fenomeno va sotto il nome "interferenza di intersimbolo": fig. 12.
Tale fenomeno è tanto più elevato quanto maggiore è il tratto di linea e quanto maggiore è la velocità di trasmissione. Tutto questo limita ovviamente la capacità di informazione della fibra che si esprime in bit/s.
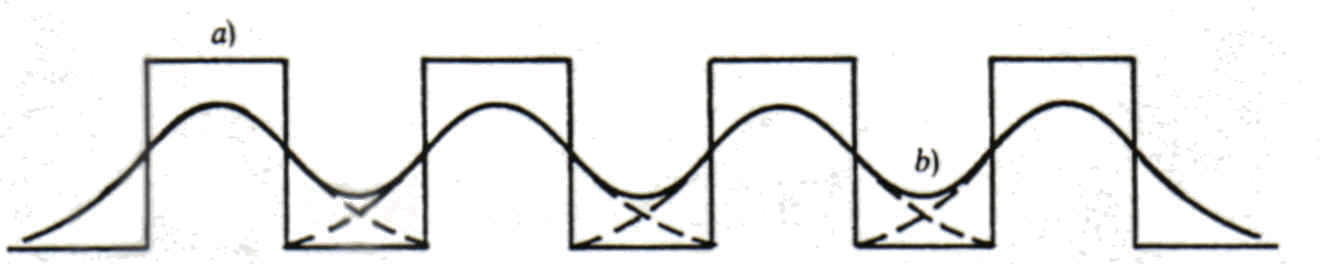
Fig. 12 Interferenza di intersimbolismo: a) Sequenza degli impulsi d'ingresso b)sequenza degli impulsi di uscita
In queste fibre multimodo con profilo d'indice a gradino (step-index) tale capacità è dell'ordine dei 100 Mbit/s per km. La capacità di informazione che si può trasmettere è legata alla lunghezza del collegamento, nel senso che se in un collegamento di 1 km è possibile trasmettere 100 Mbit/s, aumentando il collegamento a 10 km è possibile trasmettere solo 10 Mb/s; è necessario anche tenere conto della pezzatura dei cavi ottici e delle corrispondenti giunzioni; con l'aumentare della lunghezza del collegamento, aumenta il numero di tali giunzioni e quindi l'attenuazione introdotta dalle giunzioni stesse.
Si esamina ora la dispersione cromatica, t c che è dovuta a due effetti distinti:
la dispersione di materiale e la dispersione di guida.
Le sorgenti optoelettroniche non sono mai rigorosamente monocromatiche ma contengono componenti di frequenza diversa; al variare della frequenza variano sia le proprietà del materiale, sia i modi di guida. Pertanto si ha:
La dispersione cromatica da materiale in quanto l'indice di rifrazione del materiale (e quindi la velocità) è variabile al variare della frequenza: quindi componenti di frequenza diversa hanno velocità diversa e a parità di percorso hanno tempi diversi di percorrenza;
La dispersione cromatica da guida in quanto la fibra ottica è una guida d'onda anche se dielettrica; quindi l'energia elettromagnetica si propaga con un numero discreto di modi, ovvero con un numero discreto di percorsi.
Al variare della frequenza variano i modi di propagazione e quindi in termini di ottica geometrica variano gli angoli di incidenza dei raggi all'interno della guida e quindi i relativi percorsi.

Fig. 13 Dispersione cromatica al variare della lunghezza d'onda. a) Curva di dispersione cromatica da materiale; b) Curva di dispersione cromatica da guida; c) Curva di dispersione cromatica complessiva
I diagrammi della fig. 13 consentono di osservare l'andamento delle due dispersioni cromatiche in funzione della lunghezza d'onda ed il loro effetto complessivo.
Si ricava che:
La dispersione cromatica si esprime ps/nm km in quanto è definita per unità di banda (1 nm - nanometro) e per unità di lunghezza (1 km).
Il valore della dispersione cromatica è minore del corrispondente valore della dispersione modale.
Essendo la dispersione cromatica complessiva l'effetto di due dispersioni di andamento opposto, esiste una lunghezza d'onda, 1300 nm, alla quale la dispersione cromatica complessiva è praticamente nulla.
Si definisce dispersione globale, t , l'insieme degli effetti dovuti alla dispersione modale e cromatica, cioè t = t m + t c.