DAC A RESISTENZE PESATE

La figura 5 illustra lo schema circuitale di un generico DAC a resistenze pesate a n bit.

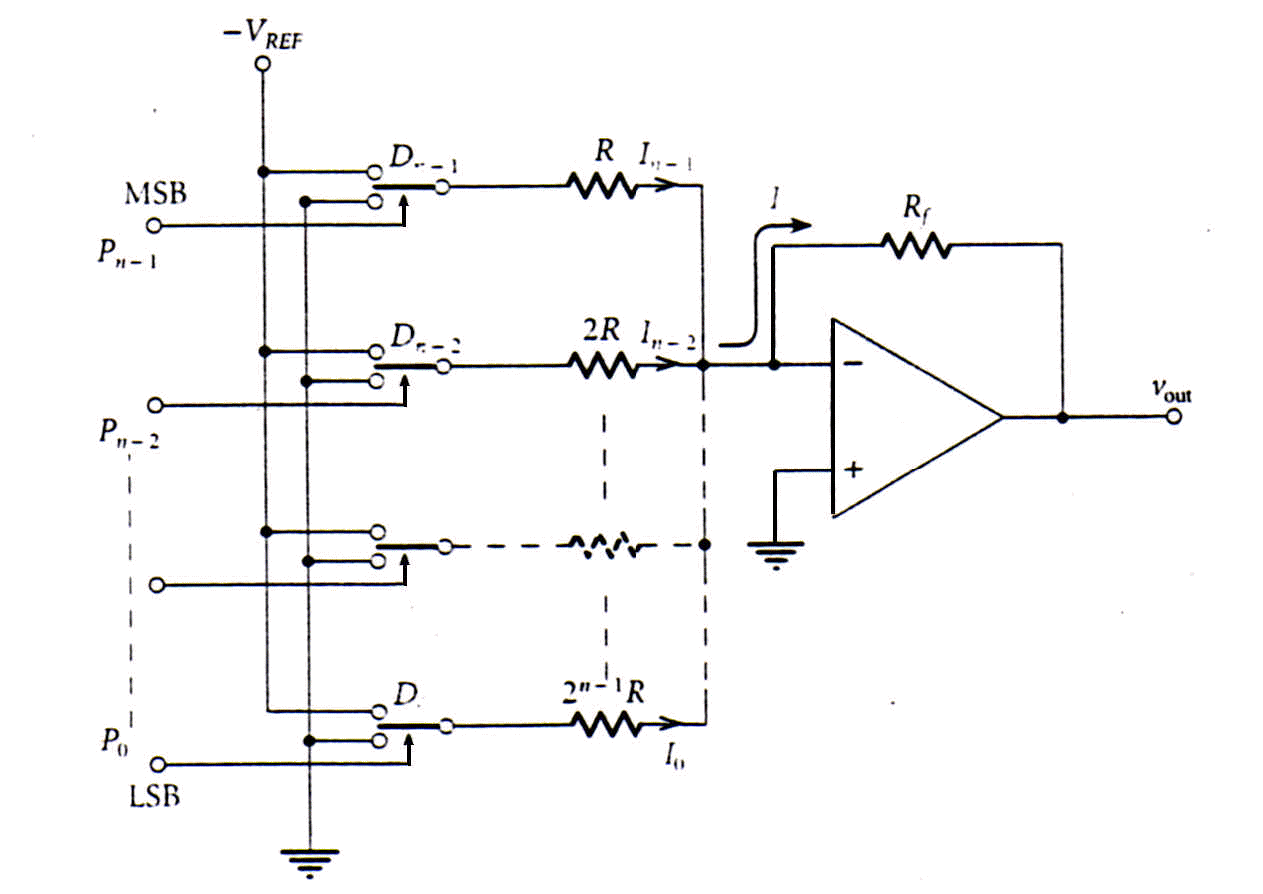
Fig. 5 Struttura circuitale di un DAC a resistenze pesate

Come si nota, il circuito è costituito da n deviatori pilotati e da un sommatore invertente i cui n ingressi sono le uscite dei deviatori. I deviatori D_n-1, D_n-1 ... D₀ sono pilotati dai corrispondenti bit P_n-1, P_n-2... P₀ della parola di ingresso in modo tale che:

• Quando il generico bit è a 1 il corrispondente deviatore viene collegato a -V_REF

• Quando lo stesso bit è a 0 il deviatore viene collegato a massa (0 V).

I rami di ingresso del sommatore sono costituiti da resistenze il cui valore è un multiplo di quello di riferimento R. Questi multipli sono "pesati" secondo potenze di 2 (da cui DAC a resistenze pesate). L'espressione di v_out in funzione della parola d’ingresso può essere determinata considerando la nota relazione di ingresso uscita di un sommatore invertente. Nel caso dei DAC, avendo presenti le topologie che verranno esaminate in seguito e le specifiche normalmente elencate nei data sheet, conviene procedere in modo diverso, cioè considerando le correnti della rete di resistenze pesate e l'operazionale retroazionato funzionante come convertitore corrente tensione. Le singole correnti si determinano facilmente a causa della massa virtuale imposta dall'operazionale. Infatti:

I_n-1=P_n-1(-V_REF/R) ; I_n-2=P_n-2(-V_REF/2R) ; ... ; I₀=P₀(-V_REF/2^n-1R)

Per effetto del convertitore corrente tensione si ha:

v_out=-Rf I

essendo:

I= I_n-1+I_n-2+... +I₀

Si ottiene, quindi, che:

v_out=V_REFRf/R(P_n-1+P_n-2/2²+... +P₀/2ⁿ)

Questa relazione può essere riscritta in forma più utile ottenendo:

v_out=V_REF(Rf/R)(2ⁿ/2^n-1)(P_n-1/2+P_n-2/2²+... +P₀/2ⁿ)=

=V_REF(Rf/R)2(P_n-1/2+P_n-2/2²+... +P₀/2ⁿ)

(9)

Questa equazione è nella stessa forma dell'equazione 4. Per confronto diretto, quindi, si ricava:

V_FS= V_REF(Rf/R)(2ⁿ/2^n-1)= V_REF(Rf/R)2

(10)

Q= V_REF(Rf/R)(1/2^n-1)

(11)

Inoltre, dalla 7 oppure dalla 8, si ricava:

V_outMAX=V_REF(Rf/R)(2ⁿ-1/2^n-1)  

(12)

L'equazione 9 definisce la relazione ingresso uscita di un DAC e, pertanto, il circuito esaminato è un DAC.

Questa soluzione circuitale, però, presenta un pesante inconveniente costruttivo. Affinché il dispositivo funzioni correttamente, le resistenze di ingresso devono assumere esattamente i valori pesati secondo le potenze di 2. In caso contrario, infatti, non è possibile ottenere la relazione 9 e il dispositivo non funziona correttamente. Il vincolo relativo ai valori delle resistenze d’ingresso è molto restrittivo, sia per le realizzazioni di questo DAC a componenti discreti (situazione rara nella quale, per attribuire a ciascuna resistenza l'esatto valore richiesto, occorre scegliere tra quelle commercialmente disponibili e di valore prossimo a quello necessario il quale, a sua volta, deve essere comunque compensato, per esempio mediante trimmer che ne permettano la taratura, con evidente compromissione della precisione) sia, soprattutto, per le soluzioni integrate. In quest'ultimo caso, infatti, l'esatta taratura dei valori resistivi comporta processi costruttivi costosi e poco convenienti anche in termini di precisione. Si pensi all'insieme di valori da attribuire alle resistenze per un normale DAC a 8 bit (n = 8). Per questi motivi sono state individuate per i DAC altre soluzioni circuitali. La più diffusa è quella della cosiddetta rete a scala R-2R.