

La logica funzionale dei DAC.
Dal punto di vista funzionale un DAC viene simbolicamente rappresentato nel modo illustrato in figura 1.
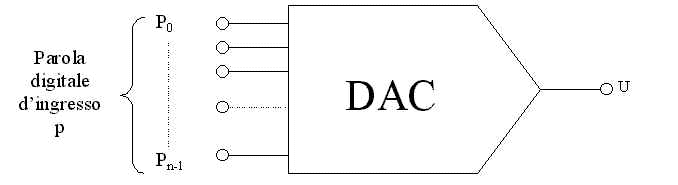
Fig. 1 Simbolo funzionale del DAC
Un DAC accetta come ingresso una parola digitale di n bit e fornisce come uscita un livello di tensione o di corrente proporzionale al valore della parola digitale di ingresso. Ripetendo questa operazione per ogni parola digitale applicata al suo ingresso, il DAC genera un’uscita costituita da livelli, per esempio di tensione, il cui valore è proporzionale alla corrispondente parola di ingresso. La figura 2 descrive in termini qualitativi un possibile andamento dell’uscita di un DAC corrispondente a diverse combinazioni di una parola digitale di ingresso di n = 3 bit. Come si nota, affinché il DAC possa generare un livello dell'uscita è necessario mantenere applicata la generica combinazione d’ingresso per un intervallo di tempo finito. Parole d’ingresso uguali (evidenziate in colore nella figura 2) producono uguali livelli di uscita.
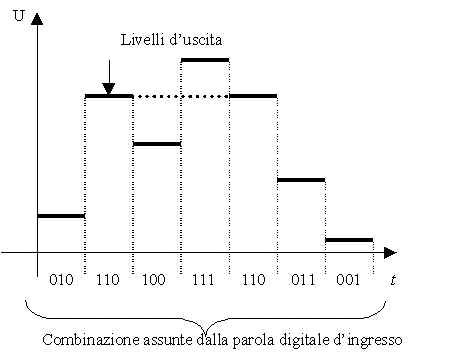
Fig. 2 Andamento di uscita di un DAC
Poiché l'uscita U di un DAC è proporzionale alla parola di ingresso P allora in termini generali si può scrivere:
U=kP
(1)
Il termine k è una costante che esprime la proporzionalità che il DAC genera tra ogni generico livello di uscita e la corrispondente parola di ingresso. Come vedremo, l'espressione e il valore di k dipendono sostanzialmente dalla topologia circuitale del DAC.
Nell'ipotesi che la parola P sia espressa in codice binario naturale a n bit, la precedente relazione risulta così esplicitata:
P=Pn-12n-1+Pn-22n-2+Pn-32n-3+...+P121+ P020
dove il generico termine P indica il bit, nella corrispondente posizione all'interno della parola, il cui valore può essere O oppure 1. In particolare, P0 è il bit meno significativo (LSB) e Pn-1 è quello più significativo (MSB).
La relazione 1, pertanto, diventa:
U=k(Pn-12n-1+Pn-22n-2+Pn-32n-3+...+P121+ P020)
(2)
Quest'ultima equazione esprime in termini generali, e per un qualsiasi DAC, la relazione tra l'ingresso digitale e il corrispondente livello di uscita.
Le principali caratteristiche funzionali di un DAC possono essere ricavate esaminando tale equazione in corrispondenza di particolari combinazioni della parola d’ingresso P. Consideriamo, infatti, le situazioni in cui:
Tutti i bit assumono valore nullo (Pn-1=Pn-2=Pn-3=... =P1=P0)
U= 0
Il bit LSB vale 1 e tutti gli altri sono nulli (Pn-1=Pn-2=Pn-3=¼ =P1=0) In questo caso l'ingresso equivale al decimale 1. Tale situazione definisce il caso più semplice di variazione minima (un solo bit) della parola di ingresso. Dalla 2 si ricava che:
U= k
Consideriamo ora la configurazione successiva, cioè quando P1 = 1 e tutti gli altri bit sono nulli. L'ingresso ora equivale al decimale 2. In questo caso, sempre dalla 2, si ottiene:
U=2k
Ne deriva che la variazione dell'uscita, prodotta dalla commutazione dell'ingresso da una configurazione a quella successiva, è:
U2-U1= k
A questo stesso risultato si giunge considerando una qualunque combinazione d’ingresso e la sua successiva.
Ciò significa che k è la variazione minima dell'uscita perché generata dalla commutazione di una combinazione d’ingresso a quella immediatamente successiva. Tale variazione minima viene anche chiamata quanto e indicata con Q. Poiché il numero delle diverse combinazioni di una parola di n bit è 2n, e k è la variazione minima dell'uscita, si definisce Fondo Scala FS (Full Scale Range) di un DAC il prodotto tra i suddetti parametri, cioè:
FS= k2n
(3)
L'equazione 2, pertanto, può essere riformulata raccogliendo il termine 2n. In tal modo si ottiene:
U = k2n(Pn-1/2+Pn-2/22+Pn-3 /23+... +P1/2n-1+ P0/2n) =
=FS(Pn-1/2+Pn-2/22+Pn-3 /23+... +P1/2n-1+ P0/2n)
(4)
Questa equazione esprime l'andamento dell'uscita in funzione anche del Fondo Scala che, in genere, è un valore (di corrente o di tensione) reperibile nei data sheet.
Dalla 3 si ricava, quindi, l'espressione del quanto Q:
Q = k = FS/2n
(5)
Il bit MSB vale 1 e tutti gli altri sono nulli (Pn-1=1 ; Pn-2=Pn-3=¼ =P1=P0=0)
Un-1 = FS/2
(6)
L'uscita si assesta a metà del Fondo Scala.
Tutti i bit sono ad 1(Pn-1=Pn-2=Pn-3=¼ =P1= P0=1).
UMAX = (FS/2n) (2n-1+2n-2+2n-3+¼ +21+20) = (FS/2n) (2n-1)
Questa relazione si comprende facilmente facendo riferimento, per esempio, al caso in cui n=3. Infatti (2n-1+2n-2+2n-3+... +21+20)=7, cioè (2n-1) = 8 - 1 = 7. Considerando l'espressione del quanto si conclude che:
UMAX= (FS/2n) (2n-1) = Q(2n-1)
(7)
Si tenga presente che il Fondo Scala non coincide con il massimo valore dell'uscita. Dalla 7, infatti, si ha:
UMAX= FS-(FS/2n)=FS-Q
(8)
Ne deriva che:
FS> UMAX