Escluso dunque il numero 2, tutti i numeri primi sono dispari.

Il controllo della primalità di un numero è la classificazione di quest'ultimo come primo o come composto.

Un "veloce" algoritmo di controllo della quasi certa primalità di numeri con un elevato numero di cifre, si basa sul cosiddetto piccolo teorema di Fermat.

Il teorema stabilisce che se p è un numero primo, allora per ogni numero naturale b appartenente all'intervallo aperto (0,p) è:

I numeri 2, 3 e 5 sono primi, e per essi è infatti:

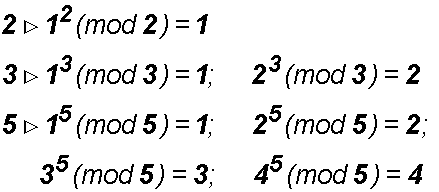
L' equivalenza logica del teorema è che: se esiste un numero naturale b appartenente all'intervallo aperto (0,p), per il quale:

è diverso da b, allora p è un numero composto.

Così ad esempio per il numero p=4 è:

per cui 4 è, come ci attendeva, composto.

E' lecito a questo punto chiedersi: se per ogni b, appartenente all'intervallo aperto (0,p), è:

si può affermare che p è un numero primo ?

Purtroppo no.

Esistono infatti numeri composti come:

- 561 (il prodotto di 3, 11 e 17)
- 1729 (il prodotto di 7, 13 e 19)

che, in relazione al piccolo teorema di Fermat, si comportano come se fossero primi.

Siffatti numeri sono detti numeri di Carmichael.

Esistono anche numeri composti che, in relazione al piccolo teorema di Fermat, si comportano come se fossero primi, ma non per tutti i valori di b dell'intervallo aperto (0,p).

Per il numero composto 341 (il prodotto di 11 e 31), è infatti:

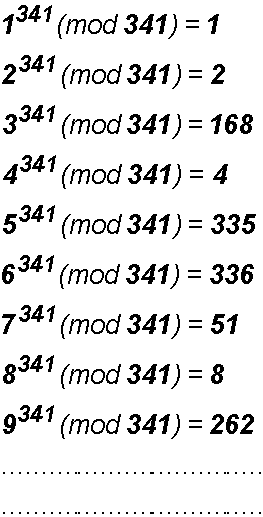
In tal caso si dice che 341 è uno pseudoprimo in base 1 - 2 - 4 - 8 - 15 - 16 - 23 - 27 - 29 - 30 - 31 - 32 - 33 - 35 - 39 - 46 - 47 - 54 - 58 - 60 - 61 - 62 - 63 - 64 - 66 - 70 - 77 - 78 - 85 - 89 - 91 - 92 - 93 - 94 - 95 - 97 - 101 - 108 - 109 - 116 - 120 - 122 - 123 - 124 - 125 - 126 - 128 - 132 - 139 - 140 - 147 - 151 - 153 - 154 - 155 - 156 - 157 - 159 - 163 - 170 - 171 - 178 - 182 - 184 - 185 - 186 - 187 - 188 - 190 - 194 - 201 - 202 - 209 - 213 - 215 - 216 - 217 - 218 - 219 - 221 - 225 - 232 - 233 - 240 - 244 - 246 - 247 - 248 - 249 - 250 - 252 - 256 - 263 - 264 - 271 - 275 - 277 - 278 - 279 - 280 - 281 - 283 - 287 - 294 - 295 - 302 - 306 - 308 - 309 - 310 - 311 - 312 - 314 - 318 - 325 - 326 - 333 - 337 - 339 - 340.

In tutto dunque 120 basi su 340.

Il numero composto 91 (il prodotto di 7 e 13), è uno pseudoprimo in base 1 - 3 - 4 - 9 - 10 - 12 - 13 - 14 - 16 - 17 - 22 - 23 - 25 - 26 - 27 - 29 - 30 - 35 - 36 - 38 - 39 - 40 - 42 - 43 - 48 - 49 - 51 - 52 - 53 - 55 - 56 - 61 - 62 - 64 - 65 - 66 - 68 - 69 - 74 - 75 - 77 - 78 - 79 - 81 - 82 - 87 - 88 e 90.

In tutto dunque 48 basi su 90.

Il numero composto 15 (il prodotto di 3 e 5), è uno pseudoprimo in base 1 - 4 - 5 - 6 - 9 - 10 - 11 e 14.

In tutto dunque 8 basi su 14.

Fortunatamente, se confrontati con i numeri primi, i numeri di Carmichael, numeri pseudoprimi in ogni base, sono molto rari, non altrettanto i numeri pseudoprimi per alcune basi (come i numeri di cui sopra: 341, 91 e 15).

Scegliamo adesso a caso una base, ad esempio del numero pseudoprimo 15.

La probabilità che quest'ultimo non venga riconosciuto come numero composto dal test di Fermat vale: 8/14=0,57.

Se risottoponiamo al test di Fermat, con una nuova base, di nuovo il numero pseudoprimo 15, la probabilità che quest'ultimo non venga ancora una volta riconosciuto come numero composto vale ora: 7/13=0,54.

Se si continua, le probabilità che si ottengono sono:
- 6/12=0,5
- 5/11=0,45
- 4/10=0,4
- 3/9=0,3
- 2/8=0,25
- 1/7=0,14.

Che, come si vede, tendono a decrescere.

E' importante a questo punto chiedersi:

se il numero pseudoprimo 15 non viene riconosciuto come numero composto per 4 volte consecutive, che probabilità ha di superare per la quinta volta il test di Fermat ?

La risposta è: 0,07=0,57*0.54*0.5*0,45.

Esclusi i numeri di Carmichael, risulta che i numeri pseudoprimi per alcune basi, sono tali, per un numero di basi b, che, al più, è circa la metà di quelli compresi nell'intervallo aperto (0,p).

Se dunque il controllo della primalità è su un numero p molto grande, scegliendo a caso 100 basi differenti, la probabilità che un numero pseudoprimo non venga riconosciuto come numero composto, nemmeno al 101-esimo test, è all'incirca minore o uguale di:

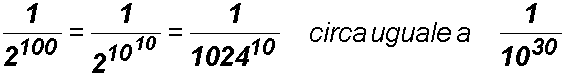
Un numero dunque che non venga, dopo 100 tentativi, riconosciuto come numero composto, dal test di Fermat, è quasi certamente un numero primo.