La struttura di una funzione modulare è la seguente
C=EP(mod m)
dove:
- E ed m sono delle costanti numeriche
- C è la variabile dipendente
- P è la variabile indipendente.

Siccome C è un resto, e dato che pensiamo di dover far ricorso alla funzione modulare inversa, in cui essendo P la variabile dipendente, anche P è un resto, allora C e P sono due numeri (0, 1, 2, 3, .....) naturali, con valori compresi fra 0 ed (m-1).

Come vedremo, la funzione C=EP(mod m) è invertibile solo se E ed m sono primi fra loro, ovvero solo se E ed m non hanno alcun fattore in comune.

Ecco un esempio: C=4P(mod 7) e relativa tabella di valori:

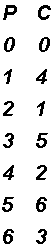
con il tipico andamento disordinato delle funzioni modulari.

La funzione inversa, che impareremo a ricavare successivamente, vale viceversa: P=2C(mod 7), come può essere verificato, "entrando", nella tabella dei valori di cui sopra, questa volta dalla colonna di destra.