Vediamo qualche esempio:
- 10(mod 4)=2
- 21(mod 45)=21
- 74(mod 7)=4
- 57(mod 57)=0
- 37(mod 36)=1 .

Con riferimento alla notazione: X(mod m)=R, valgono le seguenti proprietà:

- è sempre R < m

- tutti i possibili resti sono una quantità pari ad m e con valori compresi fra 0 ed m-1

- se X < m allora X(mod m)=X

- X(mod X)=0 ovvero m(mod m)=0

- X(mod (X-1))=1 ovvero (m+1)(mod m)=1

- X(mod 1)=0

- 0(mod m)=0.

Di notevole interesse sono le seguenti equivalenze:

- (X+Y)(mod m)=X(mod m)+Y(mod m), e cioè: il resto di una somma è pari alla somma dei resti

- (X Y)(mod m)=X(mod m) Y(mod m), e cioè: il resto di un prodotto è pari al prodotto dei resti.

Essendo resti, se uno dei due membri di un'equivalenza è maggiore o uguale a m, vuol dire che non è un resto, per cui occorre ancora dividerlo per m.

Vediamo qualche esempio:

- 17(mod 5)=2=(10+7)(mod 5)=10(mod 5)+7(mod 5)=0+2=2

- 17(mod 5)=2=(9+8)(mod 5)=9(mod 5)+8(mod 5)=4+3=7=
7(mod 5)=2

- 24(mod 5)=4=(6*4)(mod 5)=6(mod 5) 4(mod 5)=1*4=4

- 24(mod 5)=4=(8*3)(mod 5)=8(mod 5) 3(mod 5)=3*3=9=
9(mod 5)=4 .

L'equivalenza sul prodotto, conduce alla notevole equivalenza sul quadrato: il resto di un quadrato è pari al quadrato del resto. E' infatti:

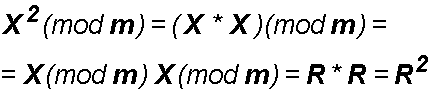
Questa proprietà sul resto di un quadrato, è di importanza fondamentale nell'ambito della crittografia a chiave pubblica con numeri primi. Come vedremo sarà grazie ad essa che sarà possibile determinare resti di divisioni fra numeri con un incalcolabile numero di cifre.

Vediamo qualche esempio:
-
-