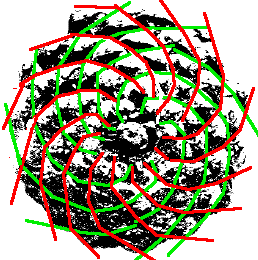
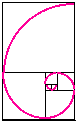
“La divina proporzione”
1/2, 1/3, 2/5, 3/8, 5/13, 8/21, 13/34…non sto dando i numeri e capisco che a prima vista queste frazioni non ci dicono granché. Vedrete invece che a volte la matematica ci circonda in maniere molto bizzarre. Cominciamo col dire il numeratore di ciascuna di esse è somma dei due numeratori delle due frazioni precedenti, ed altrettanto vale per i denominatori. I numeri che compaiono in tali frazioni: 1, 2, 3, 5, 8, 13, 21, 34…costituiscono la cosiddetta serie di Fibonacci (Leonardo, matematico pisano del 1100-1200). Ciascuno dei numeri di tale serie è la somma dei due precedenti. Tale serie è infinita e si può verificare che la serie di frazioni con cui ho aperto il mio articolo è convergente ed il valore a cui converge o tende è 0,381966… Usando questo valore si può calcolare l’angolo limite di divergenza :
0,381966 x 360°= 137° 30’ 28”
possiamo immaginare che tale angolo corrisponda ad una frazione m/n in fondo alla serie…praticamente infiniti.Il valore 0,381966… è ben noto in matematica. Infatti rappresenta la radice dell’equazione della sezione aurea.Cosa si intende per sezione aurea? Tale sezione permette di dividere un segmento in due parti tali che il rapporto tra il segmento intero e la parte più grande sia uguale al rapporto tra la parte più grande del segmento e quella più piccola, si dice così che sono medi proporzionali.Vediamo di fare due conti: supponiamo che la lunghezza del segmento sia uguale ad uno e chiamando x la parte più piccola avremo la proporzione:
da cui si ricava l’equazione di 2° grado:
Le soluzioni di questa equazione sono rappresentate dalla formula:
considerando la radice negativa abbiamo x = 0,381966…che è proprio il valore dell’angolo limite trovato prima.Per trovare la relazione che lega la sezione aurea alla serie di Fibonacci andiamo a considerare nuovamente la serie di frazioni di prima
(a) 1/2, 1/3, 2/5, 3/8, 5/13, 8/21, 13/34
e con gli stessi numeri di Fibonacci costruiamone una nuova :
(b) 1/2, 2/3, 3/5, 5/8, 8/13, 13/21, 21/34
Questa serie è complementare alla precedente infatti ciascun termine della serie (b) sommato col suo corrispondente della serie (a) da 1 (1/2+1/2; 2/3+1/3, ecc.).C’è un modo per ottenere i termini della serie (b) e cioè il numeratore di ogni frazione è uguale al denominatore della frazione precedente mentre il denominatore è uguale alla somma del numeratore e del denominatore della precedente.Più semplicemente dato un termine a/b, il successivo sarà b/(a + b).Abbiamo visto che la serie (a) tende al valore Ø = 0,381966…per cui la serie (b) dovrà tendere al valore ß =1- 0,381966…= 0,618033… più la serie progredisce e più i termini che la compongono diventano più vicini.Se uno di questi “lontanissimi termini” è x/y il successivo sarà y/(x + y).Avremo per cui:
ma questa non è altro che Ø,
la
proporzione tipica della sezione aurea scritta in maniera leggermente
diversa. In questo caso x rappresenta la parte più piccola del segmento
ed y la parte più grande. All’inizio dell’articolo avevo attirato
l’attenzione dicendo che la matematica non è solo nei libri, ed è
proprio così, infatti dopo avervi annoiato (…chi è arrivato fin qui ha
veramente pazienza) vi alcune delle forme naturali e non che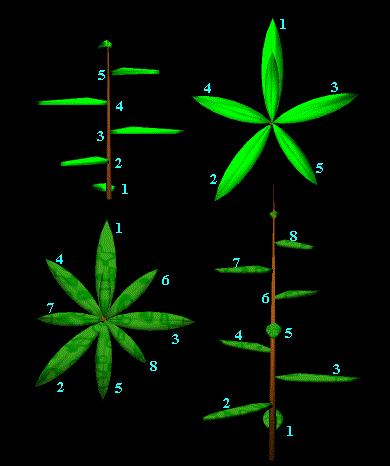
gravitano intorno a questo rapporto aureo che nel Rinascimento era
definita addirittura “divina proporzione”.Ad esempio la fillotassi
(greco phyllon
= foglia; taxis = ordine) rappresenta l’ordine con cui le foglie
sono disposte su un fusto, ordine rappresentato da una spirale che si
avviluppa in altezza non casualmente ma guarda caso seguendo la serie
creata dai numeri di Fibonacci :Un albero con fillotassi 3/8
ci indica che salendo (o scendendo) lungo la spirale abbiamo compiuto 3
giri e nel cammino incontrato 8 foglie, e tale risultato è sempre lo
stesso partendo da qualsiasi punto e il valore 3/8 x 360° è l’angolo
compreso tra due foglie consecutive. Lo scopo della natura è in questo
caso non togliere luce dalla sovrapposizione delle foglie…niente è
lasciato al caso. E le proporzioni del nostro corpo, chi più chi meno,
rispettano proprio una serie di sezioni auree. Ma vi lascio ad alcune
immagini che meglio vi faranno comprendere tutto il discorso:
