Prove a Carico
6.1 Introduzione
In questa prova il motore viene fatto funzionare come un generatore sincrono a magneti permanenti. Il prototipo, fissato su un banco di prova, viene portato in rotazione da una macchina a corrente continua. Misurando l’angolo di carico con cui il generatore è portato a lavorare, è possibile determinare i parametri della macchina. Per la prova si sono utilizzati due tipi di carico, uno puramente resistivo, ed uno di tipo ohmico induttivo, per ognuno di questi carichi si sono eseguite sia misure a velocità di rotazione costante, sia misure a velocità variabile.
La difficoltà maggiore, incontrata in questa prova, è legata alla determinazione dell’angolo di carico ![]() , definito come differenza di fase tra la forma d’onda di tensione a vuoto e quella a carico. Per rilevare quest’angolo, è stato necessario effettuare due misure in due istanti diversi nelle quali è stato necessario riprodurre la stessa velocità di rotazione. Per verificare che le due velocità fossero uguali è stato utilizzato un encoder ottico a quattro intagli.
, definito come differenza di fase tra la forma d’onda di tensione a vuoto e quella a carico. Per rilevare quest’angolo, è stato necessario effettuare due misure in due istanti diversi nelle quali è stato necessario riprodurre la stessa velocità di rotazione. Per verificare che le due velocità fossero uguali è stato utilizzato un encoder ottico a quattro intagli.
In questo capitolo si descrivono le varie prove a carico effettuate, partendo dalla descrizione dei circuiti utilizzati. Infine, dopo un’opportuna analisi critica del procedimento seguito si riportano i parametri del motore ottenuti con questa prova.
6.2 Misure su carico puramente resistivo
Per la misura su carico resistivo il circuito utilizzato è illustrato in figura 6-1. Il carico è costituito da tre resistenze uguali connesse a stella, in modo da garantire che le tre fasi del motore siano caricate allo stesso modo. Le caratteristiche delle tre resistenze sono riportate in tabella 6-1.

Figura 6-1. Schema di principio del circuito utilizzato per la prova su carico resistivo, a velocità variabile.

Tabella 6-1. Valori delle tre resistenze costituenti il carico.
Consideriamo dapprima la prova a velocità angolare variabile. Per ogni valore della velocità, si sono registrate con l’utilizzo di un oscilloscopio digitale, le forme d’onda della tensione, della corrente e del segnale dell’encoder. Con un wattmetro vettoriale si sono misurati, i valori efficaci e di fondamentale di tensione, corrente, potenza attiva e fattore di potenza ai capi del carico. Si sono inoltre rilevati con un tachimetro ed un cuplometro, i valori di velocità e coppia. Per tenere conto dell’effetto della temperatura nella determinazione dei parametri, per ogni serie di misure si è monitorata la temperatura sulla fase 3 del motore. Poiché non è possibile associare l’angolo ![]() alla differenza di fase tra gli attraversamenti a zero delle forme d’onda di tensione campionate, in quanto tali grandezze sono fortemente distorte (figura 6-2), si è dovuto ricorrere alla determinazione numerica delle fondamentali di tensione, corrente e f.e.m. a vuoto. Per tali fondamentali, si è considerato, un andamento del tipo:
alla differenza di fase tra gli attraversamenti a zero delle forme d’onda di tensione campionate, in quanto tali grandezze sono fortemente distorte (figura 6-2), si è dovuto ricorrere alla determinazione numerica delle fondamentali di tensione, corrente e f.e.m. a vuoto. Per tali fondamentali, si è considerato, un andamento del tipo:
![]() (6-1)
(6-1)
dove si è indicato con ![]() una grandezza generica. Abbiamo così determinato l’angolo
una grandezza generica. Abbiamo così determinato l’angolo ![]() come:
come:
![]() . (6-2)
. (6-2)
Nelle figure 6-2, 6-5 sono riportati gli andamenti misurati delle f.e.m. a vuoto, della tensione e della corrente sul carico, unitamente alle loro fondamentali.
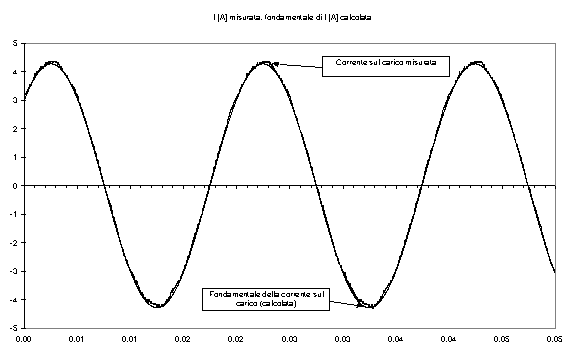
Figura 6-2. Andamento grafico della corrente misurata sul carico e della sua fondamentale.
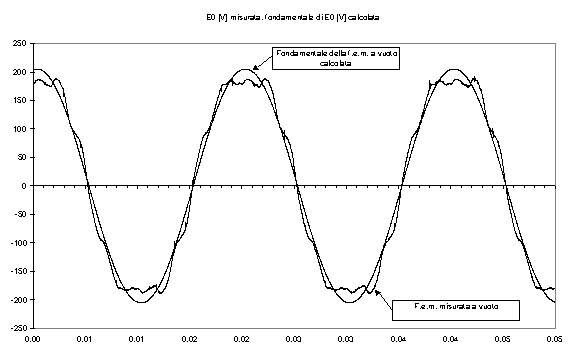
Figura 6-3. Andamento grafico della f.e.m. a vuoto misurata e della sua fondamentale.
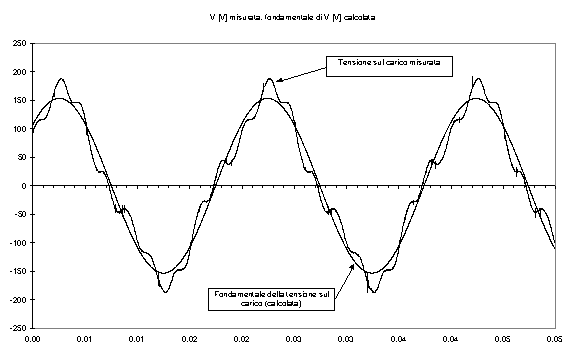
Figura 6-4. Andamento grafico della tensione misurata sul carico e della sua fondamentale.
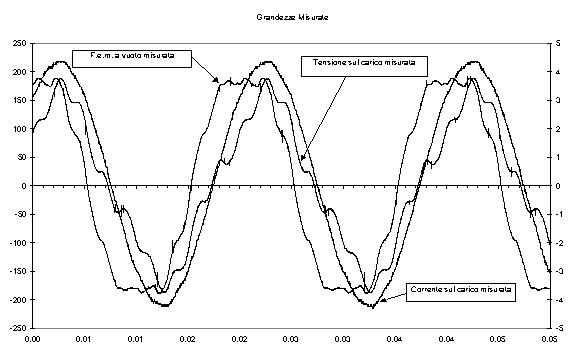
Figura 6-5. Andamento grafico della f.e.m. a vuoto, della tensione e della corrente sul carico, riferite allo stesso istante.
Ricordando il diagramma vettoriale della macchina sincrona anisotropa, riportato in figura 6-6 nell’ipotesi di carico puramente resistivo, siamo in grado di risalire alle componenti ![]() ed
ed ![]() della corrente ed alle reattanze
della corrente ed alle reattanze ![]() ed
ed ![]() .
.
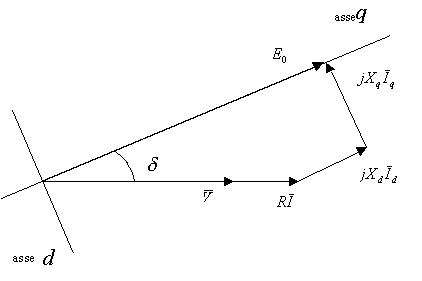
Figura 6-6. Diagramma vettoriale della macchina sincrona anisotropa, tracciato nell’ipotesi di tensione e corrente in fase.
Dal grafico, utilizzando semplici relazioni trigonometriche, si trovano immediatamente i valori di ![]() ed
ed ![]() , cioè:
, cioè:
![]() (6-3)
(6-3)
e osservando che:
![]() (6-4)
(6-4)
trovo i valori dei parametri ![]() ed
ed ![]() , in formule:
, in formule:
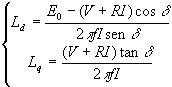 (6-5)
(6-5)
Nella tabella 6-2 sono riportati i risultati delle elaborazioni relative alla prova in esame.
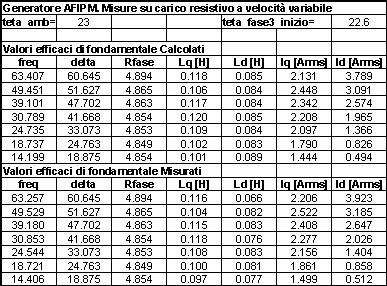
Tabella 6-2. Tabella riassuntiva dei parametri determinati con la prova su carico resistivo a velocità variabile.
Per quanto riguarda la prova fatta a velocità costante (750 rpm), il circuito usato per la misura è leggermente diverso da quello usato per la prova a velocità variabile. Tale circuito è riportato in figura 6-7.
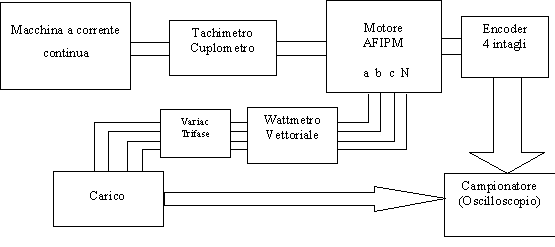
Figura 6-7. Schema di principio del circuito utilizzato per le prove su carico resistivo a velocità costante.
In particolare, è stato necessario l’utilizzo di un carico variabile in modo da poter richiedere al motore varie correnti a pari velocità. Questo è stato possibile, non disponendo di un carico resistivo variabile, con l’utilizzo di un variac trifase posto tra il motore ed il carico resistivo. In questo modo il variac è stato fatto funzionare come semplice adattatore d’impedenza. Ovviamente, l’introduzione del variac ha portato il motore a lavorare con tensione e corrente non in fase, di questo si è dovuto tenerne conto nell’elaborazione dei dati per la ricerca dei parametri. Nella figura 6-8 riportiamo il diagramma vettoriale della macchina sincrona anisotropa nell’ipotesi di ![]() .
.
Dalla figura si vede subito che l’angolo ![]() influenza i parametri
influenza i parametri ![]() ed
ed ![]() . Utilizzando lo stesso procedimento prima esposto si arriva alle seguenti espressioni:
. Utilizzando lo stesso procedimento prima esposto si arriva alle seguenti espressioni:
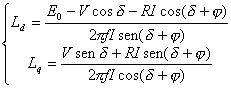 (6-6)
(6-6)
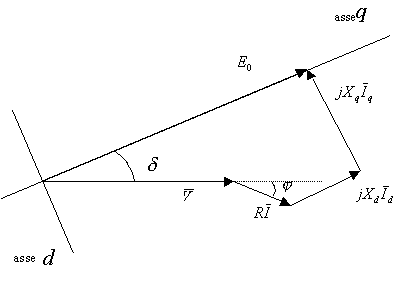
Figura 6-8. Diagramma vettoriale della macchina sincrona anisotropa, tracciato nell’ipotesi di tensione e corrente non in fase.
In tabella 6-3 sono riportati i risultati delle elaborazioni relative alla prova in esame.
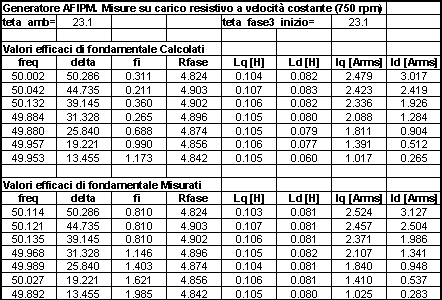
Tabella 6-3. Tabella riassuntiva dei risultati ottenuti con la prova su carico resistivo a frequenza costante.
Infine esaminiamo la prova fatta su carico R-L. In questo caso l’angolo ![]() era dell’ordine dei 60, 65 gradi, mentre l’angolo
era dell’ordine dei 60, 65 gradi, mentre l’angolo ![]() risultava dell’ordine dei 6, 7 gradi, questo ha provocato una forte sensitività dei parametri
risultava dell’ordine dei 6, 7 gradi, questo ha provocato una forte sensitività dei parametri ![]() ed
ed ![]() al valore dell’angolo
al valore dell’angolo ![]() .
.
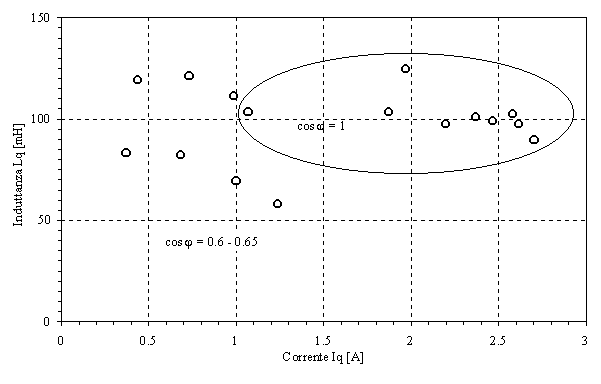
Figura 6-9. Valori dell’induttanza in asse q calcolati con due valori diversi di ![]()
La ragione di questa dipendenza dei parametri dall’angolo di carico è da ricercarsi nella definizione di angolo di carico, infatti nella determinazione di una grandezza definita come differenza di altre due grandezze molto prossime tra loro è molto facile commettere degli errori. In figura 6-9 sono riportati in modo grafico i valori dei parametri determinati utilizzando il carico R-L. Analizzando tale figura si vede come per ![]() i valori trovati sono molto variabili e non è possibile individuare un valore univoco a cui si avvicinano i punti rilevati sperimentalmente.
i valori trovati sono molto variabili e non è possibile individuare un valore univoco a cui si avvicinano i punti rilevati sperimentalmente.
6.4 Analisi dei risultati ottenuti con le prove a carico
In linea di massima con queste prove si sono ottenuti risultati coerenti con quelli ottenuti con la prova di risposta al gradino. I risultati migliori si sono ottenuti con le prove eseguite a velocità costante, in quanto in questo tipo di prove le perdite nei materiali, che dipendono dalla frequenza di lavoro, giocano sostanzialmente allo stesso modo per ogni valore di corrente. L’unico inconveniente, come già accennato nell’introduzione del capitolo, è legato al fatto che per determinare l’angolo ![]() , sono state necessarie due prove distinte nelle quali si è dovuto riprodurre la stessa velocità di rotazione. Non disponendo di un controllo di velocità, la sincronizzazione tra le velocità nelle due prove è stata condotta manualmente. Questo ha sicuramente comportato un ulteriore errore nella individuazione dell’angolo d che si è quindi ripercosso sulla determinazione dei parametri. Da notare, comunque, che con la prova a velocità costante i valori dei parametri ottenuti numericamente, risultano molto vicini a quelli ottenuti utilizzando i valori di fondamentale misurati, soprattutto per quanto riguarda i valori in asse q. Altro aspetto importante da tenere in considerazione, è legato al fatto che sia nella determinazione dei parametri utilizzando i valori di fondamentale misurati, sia utilizzando i valori calcolati, il valore dell’angolo
, sono state necessarie due prove distinte nelle quali si è dovuto riprodurre la stessa velocità di rotazione. Non disponendo di un controllo di velocità, la sincronizzazione tra le velocità nelle due prove è stata condotta manualmente. Questo ha sicuramente comportato un ulteriore errore nella individuazione dell’angolo d che si è quindi ripercosso sulla determinazione dei parametri. Da notare, comunque, che con la prova a velocità costante i valori dei parametri ottenuti numericamente, risultano molto vicini a quelli ottenuti utilizzando i valori di fondamentale misurati, soprattutto per quanto riguarda i valori in asse q. Altro aspetto importante da tenere in considerazione, è legato al fatto che sia nella determinazione dei parametri utilizzando i valori di fondamentale misurati, sia utilizzando i valori calcolati, il valore dell’angolo ![]() utilizzato è stato sempre quello calcolato numericamente, quindi l’errore commesso sull’angolo di carico ha avuto lo stesso peso nei due casi. Per quel che riguarda i risultati ottenuti con la prova a frequenza variabile, possiamo dire che anche questi sono stati soddisfacenti, in quanto indicano chiaramente quali sono i valori da considerare per
utilizzato è stato sempre quello calcolato numericamente, quindi l’errore commesso sull’angolo di carico ha avuto lo stesso peso nei due casi. Per quel che riguarda i risultati ottenuti con la prova a frequenza variabile, possiamo dire che anche questi sono stati soddisfacenti, in quanto indicano chiaramente quali sono i valori da considerare per ![]() ed
ed ![]() . L’unica prova che non ha dato un’indicazione chiara per i valori dei parametri della macchina è stata quella eseguita su carico ohmico-induttivo.
. L’unica prova che non ha dato un’indicazione chiara per i valori dei parametri della macchina è stata quella eseguita su carico ohmico-induttivo.
In tabella 6-4, sono riportati i valori numerici dei parametri del prototipo determinati con le prove a carico.

Tabella 6-4. Valori dei parametri del motore AFIPM determinati con la prova a carico.
E’ possibile, infine, fare un’osservazione legata all’influenza della temperatura su questo tipo di prova. Visto che, per la determinazione dei parametri è stato necessario effettuare due prove in istanti di tempo diversi, la temperatura raggiunta dalla macchina nelle due prove è stata sicuramente diversa. Questo significa che i materiali, le cui proprietà elettriche e magnetiche sono funzione della temperatura, hanno avuto un’influenza diversa nelle due prove. Poiché, per determinare l’angolo d si è fatto riferimento alle fondamentali di queste due grandezze calcolate in istanti diversi, si può pensare di aver commesso un errore di misura legato alla temperatura. Considerando, comunque, che questo salto termico è dell’ordine di pochi gradi, si può ritenere che l’errore legato alla temperatura sia trascurabile nella determinazione dei parametri.
Determinazione della Caratteristica
di Coppia a Velocità Nulla
7.1 Introduzione.
Con questo tipo di misure si vuole determinare la caratteristica di coppia del motore a velocità nulla, al variare dell’angolo di carico ![]() su tutti i 360° elettrici. Nota la caratteristica di coppia è possibile fare una ulteriore stima dei parametri del motore AFIPM. In questo test il motore viene portato a lavorare con correnti prossime a quelle reali di funzionamento.
su tutti i 360° elettrici. Nota la caratteristica di coppia è possibile fare una ulteriore stima dei parametri del motore AFIPM. In questo test il motore viene portato a lavorare con correnti prossime a quelle reali di funzionamento.
In questo capitolo si esaminerà il procedimento utilizzato per eseguire tale prova. In particolare si descriverà la procedura seguita per il posizionamento del motore in asse ![]() ed il metodo utilizzato per la stima della componente isotropa della coppia, del parametro
ed il metodo utilizzato per la stima della componente isotropa della coppia, del parametro ![]() e del parametro
e del parametro ![]() . Infine si farà un’analisi critica dei risultati ottenuti.
. Infine si farà un’analisi critica dei risultati ottenuti.
7.2 Posizionamento del motore in asse d.
Per il posizionamento in asse d del motore si è proceduto secondo lo schema riportato in figura 7-1. Collegate a stella le tre fasi del motore, si è alimentato con un generatore sinusoidale la fase ![]() del motore. Per verificare il posizionamento corretto in asse
del motore. Per verificare il posizionamento corretto in asse ![]() del motore, è stato necessario avere tra le fasi
del motore, è stato necessario avere tra le fasi ![]() e
e ![]() una tensione nulla. La principale difficoltà incontrata in questa fase era legata alla presenza del cogging, che rendeva difficile variare
una tensione nulla. La principale difficoltà incontrata in questa fase era legata alla presenza del cogging, che rendeva difficile variare
finemente la posizione del rotore per un corretto posizionamento in asse ![]() . Per ottenere una buona regolazione si è utilizzato il meccanismo illustrato in figura 7-2. Dopo aver portato il motore in posizione prossima all’asse
. Per ottenere una buona regolazione si è utilizzato il meccanismo illustrato in figura 7-2. Dopo aver portato il motore in posizione prossima all’asse ![]() , si sono utilizzate le due viti di regolazione in modo tale da permettere una piccola rotazione angolare dell’albero motore, garantendo contemporaneamente una coppia resistente adeguata a compensare la coppia di cogging.
, si sono utilizzate le due viti di regolazione in modo tale da permettere una piccola rotazione angolare dell’albero motore, garantendo contemporaneamente una coppia resistente adeguata a compensare la coppia di cogging.
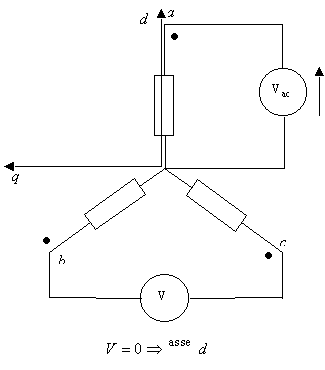
Figura 7-1. Schema di principio utilizzato per il posizionamento in asse d del motore.
Ovviamente tale posizionamento è stato possibile solo con una certa tolleranza, in quanto a bloccaggio completato, si è ottenuto tra i rami ![]() e
e ![]() una tensione dell’ordine del millivolt.
una tensione dell’ordine del millivolt.
Nella tabella 7-1, sono indicati i valori finali di tensione e corrente, risultanti dal posizionamento in esame.
|
Posizionamento del motore in asse d |
|
|
Corrente iniettata nella fase |
0,6 A |
|
Tensione indotta tra le fasi |
5 mV |
Tabella 7-1. Posizionamento in asse ![]() e conseguente errore rappresentato dai millivolt di f.e.m. indotta tra le fasi
e conseguente errore rappresentato dai millivolt di f.e.m. indotta tra le fasi ![]() e
e ![]() del motore.
del motore.
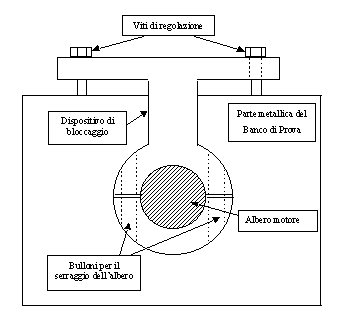
Figura 7-2. Schema indicativo utilizzato per regolare in modo fine il posizionamento dell’albero in asse ![]() .
.
Dopo aver posizionato il rotore in asse ![]() , si è proceduto ad una verifica del posizionamento, alimentando il motore in asse
, si è proceduto ad una verifica del posizionamento, alimentando il motore in asse ![]() con una corrente continua, secondo lo schema illustrato in figura 7-3. I risultati di tale verifica sono riportati in tabella 7-2.
con una corrente continua, secondo lo schema illustrato in figura 7-3. I risultati di tale verifica sono riportati in tabella 7-2.
Analizzando tali valori si può osservare che, essendo il rotore non perfettamente posizionato in asse ![]() , il motore produce coppia. Questa coppia è dovuta alla presenza di una piccola componente di corrente sull’asse
, il motore produce coppia. Questa coppia è dovuta alla presenza di una piccola componente di corrente sull’asse ![]() .
.
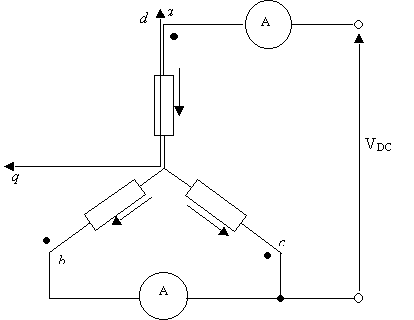
Figura 7-3. Schema di principio per l’alimentazione del motore in asse ![]() .
.
|
Coppia [Nm] |
Ia [A] |
VDC [V] |
Ic [A] |
Temp. [°C] |
|
+0,03 |
1,027 |
7,152 |
0,511 |
20,8 |
|
+0,01 |
1,998 |
13,927 |
0,996 |
20,8 |
|
0 |
3,067 |
21,419 |
1,529 |
21 |
|
-0,02 |
4,040 |
28,305 |
2,013 |
21,4 |
|
-0,04 |
4,980 |
35,110 |
2,475 |
22,4 |
|
Alimentazione invertita |
||||
|
+0,05 |
-1,010 |
-7,109 |
-0,505 |
22,6 |
|
+0,05 |
-2,005 |
-14,094 |
-1,001 |
22,6 |
|
+0,05 |
-3,007 |
-21,156 |
-1,500 |
22,7 |
|
+0,05 |
-4,020 |
-28,363 |
-2,005 |
23 |
|
+0,05 |
-4,950 |
-35,040 |
-2,468 |
23,4 |
Tabella 7-2. Misura di coppia con alimentazione DC in asse ![]() , per la verifica del posizionamento.
, per la verifica del posizionamento.
7.3 Misura del contributo di coppia isotropa del motore.
Dall’espressione (7-1), che esprime la coppia in un motore sincrono anisotropo a magneti permanenti, riferita ad un sistema di riferimento ![]() sincrono con il rotore,
sincrono con il rotore,
![]() (7-1)
(7-1)
si vede che in assenza di corrente in asse ![]() è possibile stimare il contributo di coppia isotropa del motore e successivamente il flusso
è possibile stimare il contributo di coppia isotropa del motore e successivamente il flusso ![]() dovuto al magnete.
dovuto al magnete.
Per effettuare questa misura si è alimentato il motore come indicato in figura 7-4. Per vari valori di tensione si sono rilevati i corrispondenti valori di corrente nella fase b, di coppia prodotta dal motore e di temperatura sulla fase 3. Da questi dati, ricordando che
![]() (7-2)
(7-2)
si è potuto risalire al valore di flusso ![]() prodotto dal magnete, cioè:
prodotto dal magnete, cioè:
![]() . (7-3)
. (7-3)
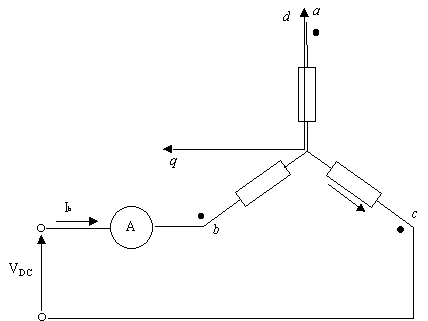
Figura 7-4. Schema di principio utilizzato per alimentare il motore in asse d per la misura della componente isotropa di coppia.
Per questa misura, il motore è stato alimentato prima con una tensione ![]() positiva, come indicato in figura 7-4, poi con una tensione
positiva, come indicato in figura 7-4, poi con una tensione ![]() negativa. Tra le due misure si è riscontrata una leggera differenza sui valori di coppia misurati, tale differenza è probabilmente legata alla presenza di attrito sui cuscinetti ed alla coppia di cogging che, nei due casi hanno contribuito in maniera diversa al valore complessivo di coppia misurata.
negativa. Tra le due misure si è riscontrata una leggera differenza sui valori di coppia misurati, tale differenza è probabilmente legata alla presenza di attrito sui cuscinetti ed alla coppia di cogging che, nei due casi hanno contribuito in maniera diversa al valore complessivo di coppia misurata.
Nelle tabelle 7-3, 7-4 sono riportati i risultati delle misure effettuate, mentre le figure 7-5, 7-6 riportano l’andamento grafico della coppia isotropa in funzione della corrente ![]() , nei due casi di alimentazione sopra citati.
, nei due casi di alimentazione sopra citati.
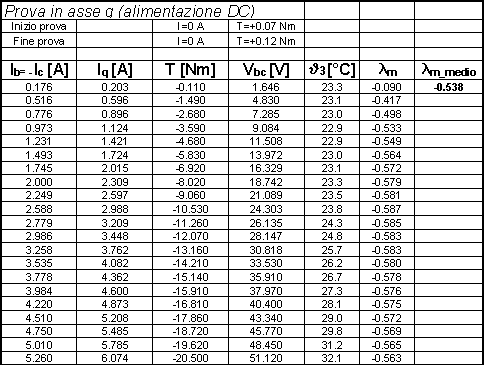
Tabella 7-3. Valori misurati della coppia in funzione della corrente ![]() e valore calcolato del flusso prodotto dal magnete, nel caso di tensione
e valore calcolato del flusso prodotto dal magnete, nel caso di tensione ![]() positiva.
positiva.
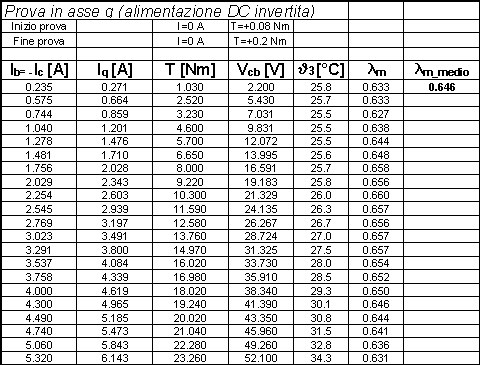
Tabella 7-4. Valori misurati della coppia in funzione della corrente ![]() e valore calcolato del flusso prodotto dal magnete, nel caso di tensione
e valore calcolato del flusso prodotto dal magnete, nel caso di tensione ![]() negativa.
negativa.
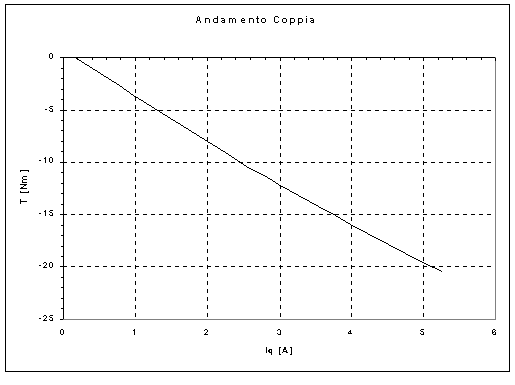
Figura 7-5. Andamento grafico della componente isotropa di coppia prodotta dal motore AFIPM in funzione della corrente ![]() , riportata nel caso di alimentazione
, riportata nel caso di alimentazione ![]() positiva.
positiva.
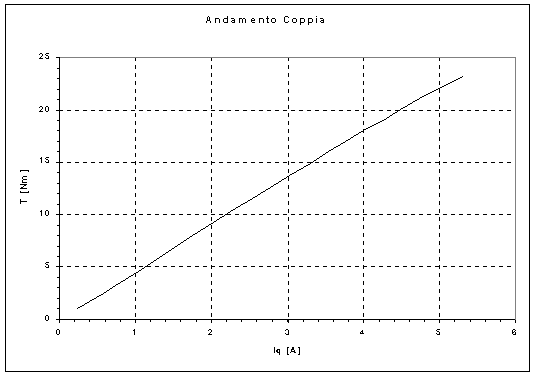
Figura 7-6. Andamento grafico della componente isotropa di coppia prodotta dal motore AFIPM in funzione della corrente ![]() , riportata nel caso di alimentazione
, riportata nel caso di alimentazione ![]() negativa.
negativa.
7.4 Determinazione della coppia in funzione dell’angolo di carico
d .Alimentando le tre fasi del motore in corrente continua è possibile misurare la coppia prodotta dal motore a velocità nulla. Elaborando tali dati è poi possibile risalire ai parametri ![]() ed
ed ![]() della macchina. In figura 7-7 è riportato lo schema di principio utilizzato per la misura.
della macchina. In figura 7-7 è riportato lo schema di principio utilizzato per la misura.
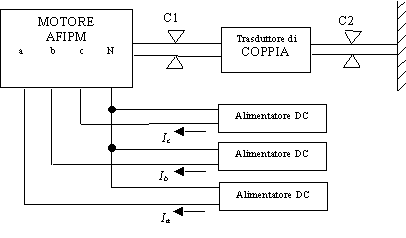
Figura 7-7. Schema di principio utilizzato per la misura della coppia al variare dell’angolo di carico d .
Per esplorare l’andamento della coppia al variare dell’angolo di carico d in tutti i 360° elettrici, bisogna alimentare le tre fasi del motore con tre correnti tali da realizzare un vettore corrente costante in modulo e rotante su tutti i 360°, vedi figura 7-8. Deve inoltre, risultare nulla la somma delle correnti iniettate nelle tre fasi, questo è importante per simulare in modo corretto il funzionamento del motore.
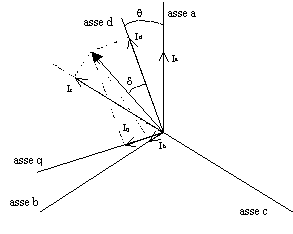
Figura 7-8. Vettore spaziale I e sue componenti in assi (a, b, c) ed in assi (d, q).
La figura 7-9 illustra lo schema elettrico di principio, necessario per realizzare tale misura.
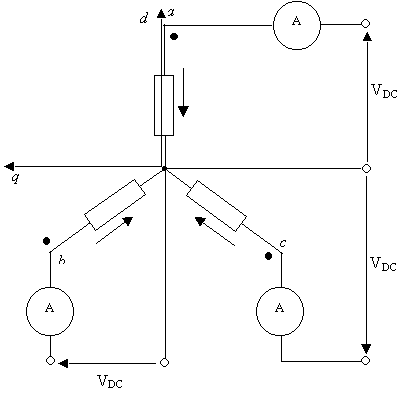
Figura 7-9. Schema elettrico utilizzato per alimentare il motore con il vettore spaziale di corrente I.
Dopo aver determinato i valori che dovevano assumere le tre componenti del vettore I sulla terna di assi ![]() in modo da ottenere il vettore spaziale corrente di modulo costante desiderato, si è proceduto praticamente ad alimentare il motore con questi valori di corrente. Tale operazione è stata condotta manualmente, ed il livello di precisione ottenuto è stato dell’ordine del milliampere. In queste misure abbiamo rilevato, per ogni posizione del vettore I, i valori corrispondenti di coppia e di temperatura. I dati sperimentali così ottenuti sono stati elaborati al fine di determinare i parametri del motore
in modo da ottenere il vettore spaziale corrente di modulo costante desiderato, si è proceduto praticamente ad alimentare il motore con questi valori di corrente. Tale operazione è stata condotta manualmente, ed il livello di precisione ottenuto è stato dell’ordine del milliampere. In queste misure abbiamo rilevato, per ogni posizione del vettore I, i valori corrispondenti di coppia e di temperatura. I dati sperimentali così ottenuti sono stati elaborati al fine di determinare i parametri del motore ![]() ed
ed ![]() . Partendo dalle componenti di corrente in assi
. Partendo dalle componenti di corrente in assi ![]() si è risalito utilizzando le trasformazioni trifase-bifase, illustrate in appendice 1, alle componenti in assi
si è risalito utilizzando le trasformazioni trifase-bifase, illustrate in appendice 1, alle componenti in assi ![]() . Da questo riferimento utilizzando le trasformazioni di rotazioni, anch’esse illustrate in appendice 1, si è arrivati alle componenti in assi
. Da questo riferimento utilizzando le trasformazioni di rotazioni, anch’esse illustrate in appendice 1, si è arrivati alle componenti in assi ![]() . Ricordando la relazione 7-1, che esprime la coppia per una macchina sincrona anisotropa a magneti permanenti in assi
. Ricordando la relazione 7-1, che esprime la coppia per una macchina sincrona anisotropa a magneti permanenti in assi ![]() , si può risalire ai valori dei parametri desiderati utilizzando dei procedimenti numerici. Possiamo ora osservare che, se il rotore fosse stato posizionato con precisione in asse d, la trasformazione di rotazione sarebbe stata superflua, in quanto in questo caso l’angolo d e l’angolo J sarebbero risultati coincidenti. I risultati ottenuti con queste misure sono riportati in tabella 7-5.
, si può risalire ai valori dei parametri desiderati utilizzando dei procedimenti numerici. Possiamo ora osservare che, se il rotore fosse stato posizionato con precisione in asse d, la trasformazione di rotazione sarebbe stata superflua, in quanto in questo caso l’angolo d e l’angolo J sarebbero risultati coincidenti. I risultati ottenuti con queste misure sono riportati in tabella 7-5.
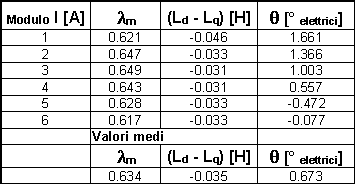
Tabella 7-5. Risultati ottenuti dalla determinazione dei parametri attraverso la misura di coppia con rotore bloccato in asse d.
Nelle elaborazioni di questi dati, è stato necessario tenere presente che queste misure di coppia sono state eseguite a motore fermo, questo ha necessariamente determinato degli errori legati alla presenza degli attriti nei cuscinetti ed alla presenza del cogging. Per tenere conto di questi errori nelle elaborazioni dei dati si sono considerate le grandezze misurate depurate dall’offset. Questo in quanto si può immaginare che gli errori sopra citati, abbiano influito sulle misure sempre allo stesso modo (stesso segno).
Si è infine tentato di stimare il contributo di coppia dovuto all’anisotropia del motore. Ricordando che in una macchina sincrona anisotropa, l’andamento della coppia in funzione dell’angolo di carico si può pensare come somma di due sinusoidi, una fondamentale dovuta in questo caso alla presenza del magnete ed una seconda armonica dovuta alla presenza dell’anisotropia. Tale andamento è riportato in figura 7-10. Per estrapolare dai dati misurati i valori di fondamentale e di seconda armonica, si è considerato per la coppia un andamento del tipo:
![]() (7-2)
(7-2)
Elaborando i dati con l’utilizzo del metodo dei minimi quadrati ed ottimizzando con il risolutore di Excel si sono ottenuti per ![]() ed
ed ![]() i valori riportati in tabella 7-6.
i valori riportati in tabella 7-6.
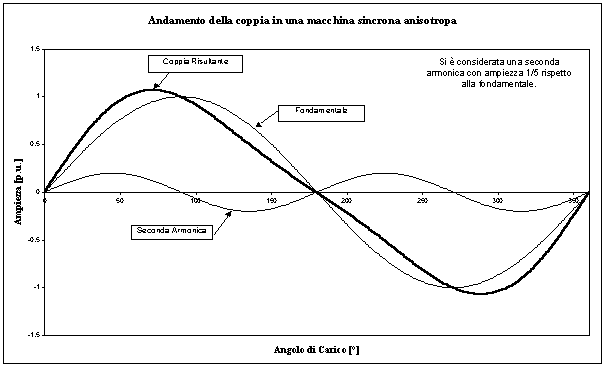
Figura 7-10. Andamento qualitativo della coppia in una macchina sincrona anisotropa.

Tabella 7-6. Valori ottenuti per A1 ed A2 e loro rapporto (A1/A2) al variare del modulo della corrente I, nel caso in cui il rotore era bloccato in asse d.
Osservando i dati riportati in tabella 7-6 si può notare come, al crescere della corrente il rapporto tra le due ampiezze decresce, questo indica che per correnti maggiori l’anisotropia del motore da un contributo sempre crescente al valore della coppia prodotta dalla macchina. Riportiamo in figura 7-11 l’andamento grafico della coppia misurata e di quella stimata con l’utilizzo della relazione 7-1, ed in figura 7-12 l’andamento grafico della coppia misurata e di quella stimata con la relazione 7-2.
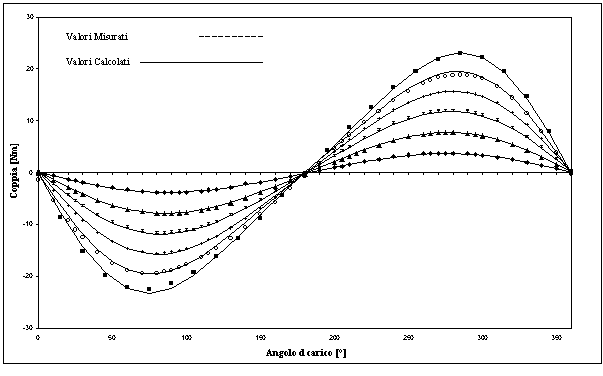
Figura 7-11. Andamento della coppia misurata e della coppia stimata con la relazione X-1, per correnti di 1 A, 2A, 3A, 4A, 5A, 6A.
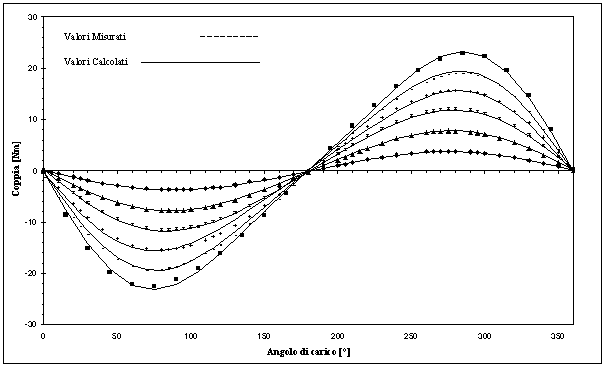
Figura 7-12. Andamento della coppia misurata e della coppia stimata considerando una fondamentale ed una seconda armonica, per correnti di 1 A, 2A, 3A, 4A, 5A, 6A.
Dopo aver completato questa prima serie di prove, effettuate con il motore bloccato in asse d, si proceduto ad una seconda serie di prove del tutto identiche a quelle appena illustrate, con l’unica differenza che il rotore non era più posizionato in asse d, ma era stato bloccato in una posizione generica e diversa dall’asse d. Lo scopo fondamentale di questa seconda serie di prove è stato essenzialmente quello di verificare i risultati ottenuti con il rotore bloccato in asse d, partendo da una condizione iniziale diversa.
Si riportano di seguito le tabelle con i risultati ottenuti in questa prova ed i grafici relativi.
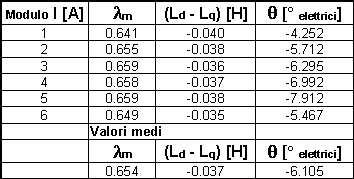
Tabella 7-7. Risultati ottenuti dalla determinazione dei parametri attraverso la misura di coppia con rotore bloccato in una posizione generica diversa dall’asse d.

Tabella 7-8. Valori ottenuti per A1 ed A2 e loro rapporto (A1/A2) al variare del modulo della corrente I, nel caso in cui il rotore era bloccato in una posizione diversa dall’asse d.
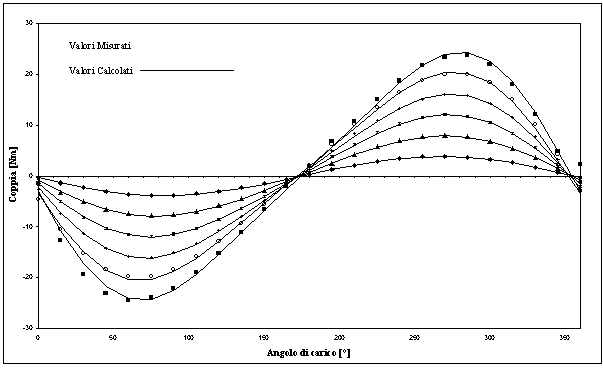
Figura 7-13. Andamento della coppia misurata e della coppia stimata con la relazione X-1, per correnti di 1 A, 2A, 3A, 4A, 5A, 6A, nel caso in cui il rotore si trovi in posizione diversa dall’asse d.
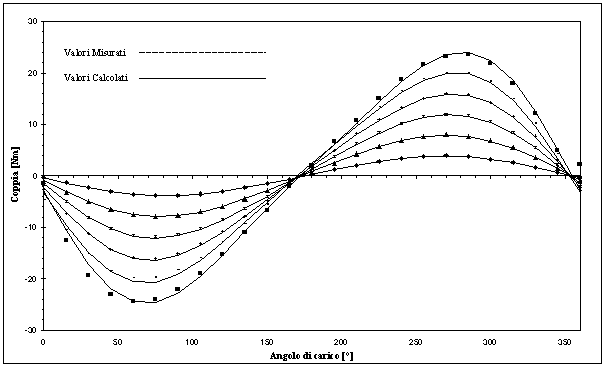
Figura 7-14. Andamento della coppia misurata e della coppia stimata considerando una fondamentale ed una seconda armonica, per correnti di 1 A, 2A, 3A, 4A, 5A, 6A, nel caso in cui il rotore si trovi in una posizione diversa dall’asse d.
7.5 Analisi dei risultati ottenuti.
Dall’analisi dei risultati, si può osservare che i valori dei parametri determinati con queste prove, confermano sostanzialmente i risultati ottenuti con le altre prove effettuate, eccezion fatta per i risultati trovati con i test in frequenza. Si può infatti osservare che la differenza ![]() è in buon accordo con i valori di
è in buon accordo con i valori di ![]() ed
ed ![]() , trovati con i test a carico.
, trovati con i test a carico.
Per agevolare tale confronto si riportano nella tabella 7-9 i valori determinati nelle due prove.

Tabella 7-9. Tabella riassuntiva dei risultati ottenuti con la prova a carico e le misure di coppia da fermo del motore AFIPM.
Non bisogna però dimenticare che nelle misure di coppia da fermo, gli errori commessi sono sicuramente maggiori rispetto a quelli commessi nelle prove a carico. Questo è da ricercarsi nella natura stessa della definizione di misura di coppia da fermo.
Quando si misura una coppia con motore fermo, in realtà quello che si misura non è proprio la coppia prodotta dal motore, ma è una coppia che comprende anche gli attriti. Purtroppo l’influenza di questi attriti sulla misura non sono facilmente valutabili, in quanto le variabili da considerare sono molteplici. Ne consegue che, anche se i risultati sono buoni, tale prova risulta meno attendibile ai fini della determinazione dei parametri del motore.
Misura Del Cogging
8.1 Introduzione
La presenza dei magneti sul rotore del prototipo in esame, pone problemi dovuti alla presenza del cogging. Tale coppia è presente anche con motore non alimentato, in quanto è dovuta a condizioni energetiche, massima e minima riluttanza del percorso magnetico, legate alla posizione reciproca tra rotore e statore. In questo capitolo si analizzeranno con maggiore dettaglio le cause che provocano tale disturbo, il procedimento utilizzato per la misura ed infine si farà un’analisi critica dei risultati ottenuti.
Per spiegare in modo più o meno semplificato le cause che portano alla nascita del cogging in una macchina a magneti permanenti, facciamo riferimento ad una macchina a flusso radiale. La figura 8-1 illustra lo schema di principio di tale macchina.
Guardando la figura 8-1b, si vede chiaramente che quando il rotore è in posizione A il percorso magnetico, risulta a riluttanza minima in quanto il flusso del magnete vede un dente di statore. Quando invece il rotore si trova in posizione B il percorso magnetico è a riluttanza massima, in quando il flusso del magnete vede di fronte a se una cava di statore. Da questo si capisce che il sistema è in una condizione di minima energia quando il rotore è in posizione A. Quindi, non appena si cerca di spostare il rotore dalla posizione A, nasce una coppia (cogging) che dapprima tende a riportare il sistema nella posizione A di minima energia, mentre non appena supera un certo angolo tende a portare il sistema in una posizione diversa dalla A ma analoga energeticamente, in pratica sotto il dente successivo. Si può infatti osservare che le posizioni A e B sono periodiche con periodo pari al passo di dentatura.
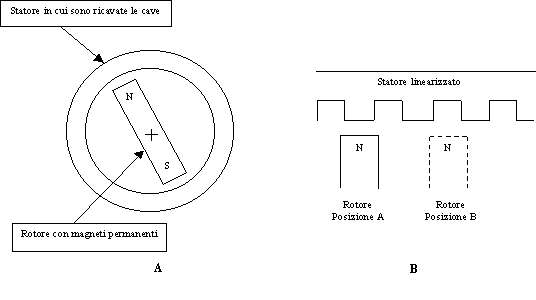
Figura 8-1. A) Schema di principio di una macchina a flusso radiale con rotore a magneti permanenti;
B) Modello linearizzato della macchina di figura A.
L’effetto descritto sopra si riferisce ad una sezione infinitesima ortogonale all’asse della macchina, bisogna tenere conto che lo stesso fenomeno si ripete per ogni sezione lungo tutto l’asse della macchina. Quindi la coppia risultante che ne deriva ha un’ampiezza non trascurabile. Bisogna allora prendere dei provvedimenti per rendere tale coppia minima compatibilmente con le applicazioni cui è destinata la macchina. Questo è possibile facendo in modo che i denti di statore, tra le due sezioni estreme della macchina, risultino ruotati di circa un passo-cava. La figura 8-2 illustra graficamente tale procedimento.
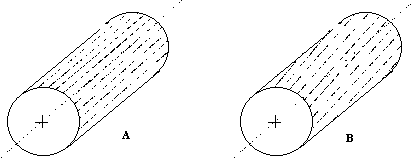
Figura 8-2. A) Esempio di statore con cave disposte assialmente;
B) Esempio di statore in cui sono stati presi provvedimenti per ridurre il cogging, le cave
sono state ruotate di un passo di dentatura.
Ovviamente tutto quello che è stato detto per la macchina a flusso radiale, può essere ripetuto, tenendo conto delle diversità costruttive, per la macchina a flusso assiale.
Una differenza sostanziale che vale la pena ricordare, riguarda il provvedimento utilizzato per ridurre il cogging. Nel prototipo AFIPM in studio, per la riduzione del cogging non si sono ruotate le cave di statore ma si sono presi provvedimenti sul rotore stesso. In particolare, i tagli sulle ferriti che ricoprono i magneti sono stati fatti in direzione non radiale, sperando di avere lo stesso effetto di riduzione del cogging ottenuto con il metodo illustrato in figura 8-2. La figura 8-3 illustra schematicamente il provvedimento adottato per la macchina AFIPM in studio.
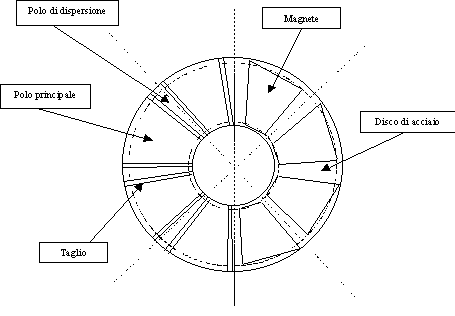
Figura 8-3. La figura illustra il rotore del prototipo AFIPM, in particolare il lato sinistro della
figura mostra il rotore completo con le ferriti, mentre il lato destro mostra la
struttura interna del rotore, in assenza delle ferriti.
Per la misura del cogging a motore non alimentato, si è proceduto secondo lo schema di principio illustrato in figura 8-4.
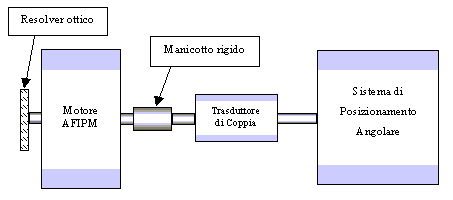
Figura 8-4. Schema di principio utilizzato per la misura del cogging del prototipo AFIPM.
Il motore è stato collegato tramite un manicotto rigido ad un trasduttore di coppia. Il trasduttore di coppia a sua volta è stato collegato ad un sistema di posizionamento angolare, necessario per ruotare l’albero del motore con piccoli angoli. Il sistema di posizionamento angolare, illustrato in figura 8-5, consiste in una puleggia in cui sono ricavate delle scanalature in direzione ortogonale all’asse di rotazione, un sottile filo d’acciaio, un sistema di pesi ed una barra filettata. La barra filettata è stata vincolata tramite una filettatura su di un supporto precedentemente fissato al banco di prova. Sull’estremità superiore della barra filettata è stato realizzato un sistema con dado e controdado, per permettere la regolazione angolare dell’albero mediante rotazione destrosa o sinistrosa della barra stessa. A tale barra è stata fissata un’estremità del filo d’acciaio, che dopo un certo numero di giri attorno alla puleggia è stato vincolato con l’altra estremità al sistema di pesi. La funzione del sistema di pesi è stata quella di compensare la coppia di cogging.
Noto il passo di filettatura (1 mm), noto il numero di giri fatti dalla barra filettata e noto il diametro della puleggia (120 mm), è stato immediato risalire all’angolo di cui si era mosso l’albero del motore, cioè:
![]() (8-1)
(8-1)
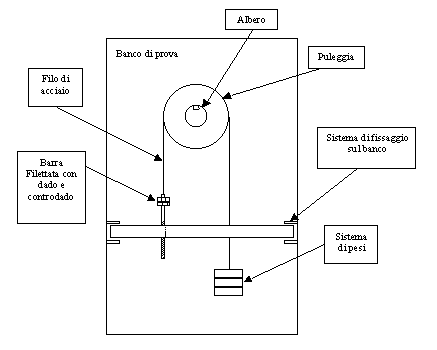
Figura 8-5. Sistema di posizionamento angolare utilizzato per il rilevare la posizione dell’albero motore nella misura del cogging.
Per la misura si è proceduto facendo avanzare la barra filettata per quarti di giro, in modo da avere un numero sufficientemente elevato di punti per descrivere adeguatamente la forma e l’ampiezza del cogging. In ogni posizione assunta dal rotore si è misurata la coppia prodotta. Per avere una descrizione migliore della forma d’onda si sono esplorati circa quattro periodi, sia facendo ruotare la puleggia in senso orario che in senso antiorario. La figura 8-6 mostra l’andamento del cogging in funzione dell’angolo tra rotore e statore.
Analizzando la figura 8-6, è evidente la presenza di una coppia costante, dovuta alla presenza di attriti, che trasla verso l’alto o verso il basso la forma d’onda misurata del cogging. A conferma di quanto detto, si è proceduto a depurare dall’offset le grandezze misurate, il risultato è stato una discreta sovrapposizione delle due forme d’onda. La figura 8-7 mostra le forme d’onda senza l’offset. Ovviamente partendo da dati affetti da un errore, non è stato possibile arrivare con una semplice elaborazione numerica ad un risultato soddisfacente. Si è allora proceduto ad un’ulteriore misura.
Posizionato il rotore in una posizione diversa da quella in cui è stata svolta la precedente misura, si è allentata la presa del manicotto in modo da ridurre al minimo l’effetto degli attriti sui cuscinetti, dovuti ad un eventuale disassamento tra l’albero motore e l’albero del banco.
Le figure 8-8, ed 8-9 mostrano i risultati di tale misura.
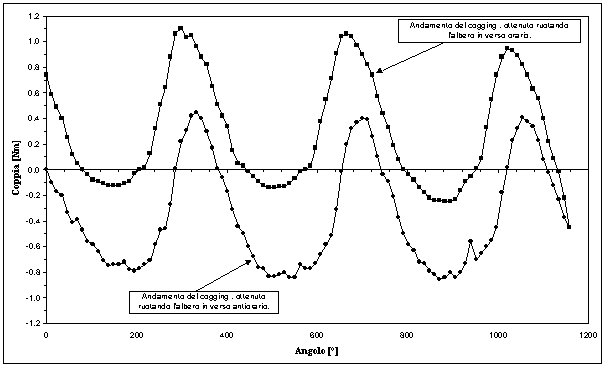
Figura 8-6. Andamento della coppia di cogging in funzione della posizione reciproca tra rotore e statore, determinato nel caso di manicotto completamente inserito.
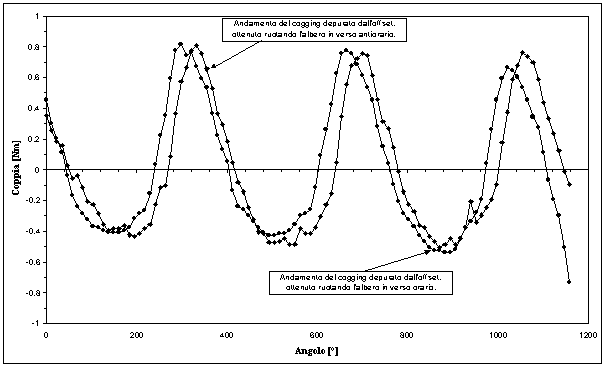
Figura 8-7. Andamento della coppia di cogging, depurata dall’offset, in funzione della posizione reciproca tra rotore e statore, determinato nel caso di manicotto completamente inserito.
Dall’analisi della figura 8-8 si vede un netto miglioramento dei risultati, in particolare l’effetto dell’attrito è stato notevolmente ridotto. Questo risultato ha confermato sostanzialmente il procedimento utilizzato per la misura, e ne ha messo in evidenza i suoi limiti. Purtroppo nelle misure a motore fermo gli attriti giocano un ruolo importante e non è possibile fare una stima accurata del loro effetto per poterne tenere conto.
Da queste misure si vede che pur adottando i provvedimenti illustrati nel paragrafo precedente, il motore mostra una coppia di cogging il cui valore (circa ![]() picco-picco) non è affatto trascurabile.
picco-picco) non è affatto trascurabile.
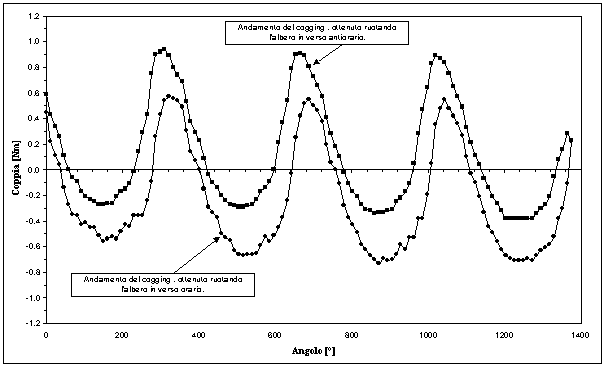
Figura 8-8. Andamento della coppia di cogging in funzione della posizione reciproca tra rotore e statore, determinato nel caso di manicotto non completamente inserito.
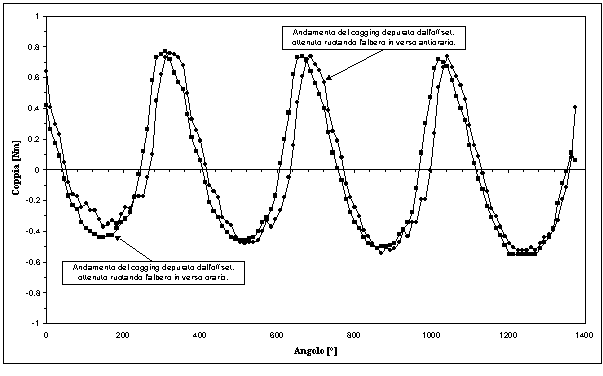
Figura 8-9. Andamento della coppia di cogging, depurata dall’offset, in funzione della posizione reciproca tra rotore e statore, determinato nel caso di manicotto non completamente inserito.
Caratterizzazione Magnetica del Materiale SomalloyTM 500
9.1 Introduzione
L’impiego di un materiale ferromagnetico, nella costruzione di macchine elettriche, richiede la conoscenza delle sue caratteristiche magnetiche. Di fondamentale importanza è la conoscenza della relazione che lega l’induzione magnetica al campo magnetico nel materiale. Questa relazione è generalmente fornita in forma grafica.
In figura 9-1, è riportato in modo qualitativo l’andamento di tali curve, tracciate nell’ipotesi di materiale inizialmente smagnetizzato e sottoposto ad un campo magnetico H variabile tra due valori simmetrici. In tale grafico, si distingue la curva di prima magnetizzazione (rappresentata con la linea tratteggiata) ed il ciclo d’isteresi statico del materiale (curva polidroma non lineare).
In figura 9-2 è riportata la caratteristica di normale magnetizzazione, definita come luogo geometrico degli estremi di cicli d’isteresi simmetrici di ampiezza via via crescente. Tale curva ha un andamento poco diverso dalla curva di prima magnetizzazione, in essa si possono distinguere tre zone rettilinee raccordate con due archi di circonferenza. Un primo tratto di estensione molto limitata in cui la permeabilità non è molto elevata, un secondo tratto in cui la permeabilità è molto elevata ed il comportamento del materiale è pressoché lineare ed un terzo tratto con pendenza molto ridotta e quindi con permeabilità molto bassa.
In riferimento ad un punto P sulla curva di normale magnetizzazione, si definisce permeabilità normale l’inclinazione, rispetto all’asse delle ascisse, della retta passante per il punto P e per l’origine degli assi. Da questa definizione, si capisce che in un materiale ferromagnetico la permeabilità normale è funzione del punto P in cui il materiale è portato a lavorare.
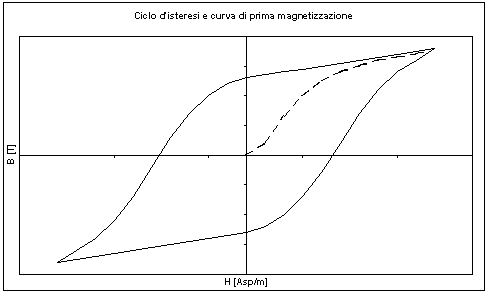
Figura 9-1. Ciclo d’isteresi statico e curva di prima magnetizzazione (linea tratteggiata) per un materiale ferromagnetico.
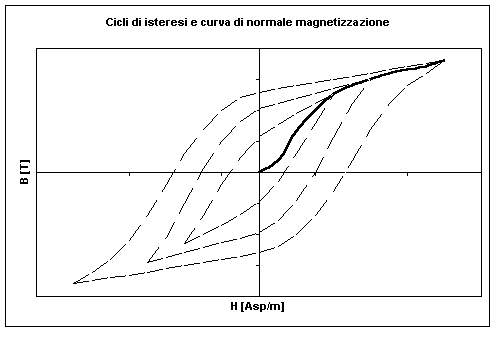
Figura 9-2. Curva di normale magnetizzazione (luogo geometrico degli estremi di cicli d’isteresi simmetrici di ampiezza crescente).
9.2 Perdite nei materiali ferromagnetici
Quando un materiale ferromagnetico è chiamato a lavorare in regime variabile, diventa sede di perdite. In questi materiali le perdite possono essere attribuite a due cause, la prima dovuta all’isteresi magnetica, la seconda alla presenza di correnti parassite.
Abbiamo visto che un materiale ferromagnetico, soggetto ad un campo variabile tra due valori simmetrici, descrive nel piano B-H un ciclo d’isteresi statico. L’area del ciclo rappresenta l’energia perduta, per isteresi, dal materiale per unità di volume nel ciclo considerato. Per cicli simmetrici, la relazione che lega le perdite per isteresi all’area del ciclo, o meglio al valore massimo dell’induzione, è data in maniera empirica dalla seguente relazione:
![]() (9-1)
(9-1)
dove kh è una costante dipendente dal materiale ed n una costante di valore compreso tra 1,6 e 2,2.
Poiché i materiali ferromagnetici, sono anche dei discreti conduttori di corrente, le variazioni di flusso inducono delle f.e.m. che a loro volta provocano la circolazione di correnti che danno luogo a perdite per effetto Joule (perdite per correnti parassite). La relazione che esprime le perdite per correnti parassite è la seguente:
![]() (9-2)
(9-2)
dove kcp è una costante che dipende dalla natura del materiale e kf è il fattore di forma dell’induzione (o della tensione), espresso come rapporto tra il valore efficace ed il valore medio dell’induzione. Queste perdite dipendono dal fattore di forma dell’induzione in quanto sono legate al valore efficace della f.e.m. indotta.
Da notare che il ciclo d’isteresi può anche essere rilevato dinamicamente con l’uso di un oscilloscopio e di una eccitazione alternata, in tal caso il ciclo di isteresi risulta più grande del ciclo d’isteresi rilevato staticamente e la sua area rappresenta le perdite totali per isteresi e correnti parassite, in un ciclo e per unità di volume.
Per ridurre tali perdite nelle applicazioni non si utilizza il ferro massiccio, ma in genere le parti in ferro sono laminate, inoltre per aumentare la resistività del ferro e ridurre l’area del ciclo d’isteresi viene aggiunto del silicio.
9.3 Provino utilizzato per le misure
Il materiale testato è costituito da polveri di ferro opportunamente pressate, i cui granuli sono singolarmente isolati l’uno dall’altro allo scopo di ridurre il percorso delle correnti indotte.
Per le misure magnetiche si sono utilizzati tre toroidi incollati insieme (come mostrato in figura 9-3), le cui caratteristiche sono riportate nella tabella 9-1. Il tutto è stato poi ricoperto con un sottile strato di nastro, il cui scopo era semplicemente quello di proteggere l’isolante dei conduttori, costituenti l’avvolgimento, contro eventuali abrasioni.

Tabella 9-1. Caratteristiche geometriche dei toroidi utilizzati per le misure.
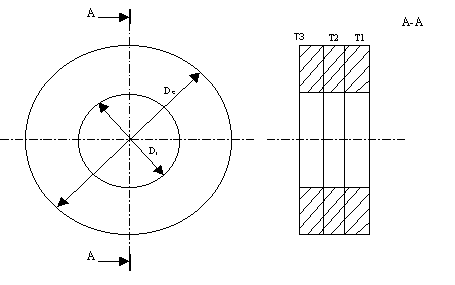
Figura 9-3. Disegno costruttivo del provino utilizzato per le misure.
Sul provino toroidale sono stati realizzati tre avvolgimenti sovrapposti e distribuiti uniformemente, un avvolgimento di misura, uno di eccitazione ed uno di polarizzazione, le cui caratteristiche sono riportate nella tabella 9-2. L’avvolgimento di misura è stato realizzato a strettissimo contatto con il materiale da testare per ridurre al minimo la quantità di flusso disperso, gli altri due sono stati realizzati al di sopra dell’avvolgimento di misura.
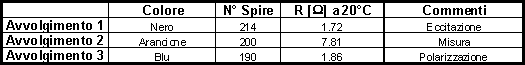
Tabella 9-2. Caratteristiche degli avvolgimenti utilizzati per le misure.
L’avvolgimento di polarizzazione, necessario per simulare la presenza del magnete, è giustificato dalla necessità di studiare il comportamento del materiale in presenza di polarizzazione e di piccolo segnale di eccitazione. Questo, in quanto i test in frequenza effettuati sul motore, sono stati fatti con un segnale molto piccolo, ed in presenza dei magneti del motore che portano il materiale ferromagnetico a lavorare in presenza di polarizzazione.
9.4 Rilievo della curva B-H e determinazione della cifra di perdita
Le misure effettuate sul toroide possono essere suddivise in due gruppi, il primo gruppo volto a determinare la permeabilità relativa e le perdite nel materiale, il secondo volto a determinare la permeabilità differenziale del materiale.
Il circuito di misura è riportato in fig. 9-4, da notare che nel blocco di eccitazione è presente sia un variac che un gruppo generatore di funzione-amplificatore di potenza, che verranno utilizzati alternativamente in funzione del tipo di alimentazione richiesto dalle varie misure.
In realtà, la forma d’onda in uscita dal blocco di eccitazione, sia nell’uno che nell’altro caso, non è perfettamente sinusoidale ma leggermente distorta, questo può provocare qualche errore nella valutazione delle grandezze, che sono state ricavate nell’ipotesi di grandezze sinusoidali.
Nell’ipotesi fatta, di grandezze sinusoidali, si può supporre che il flusso concatenato con l’avvolgimento di misura sia esprimibile come:
![]() (9-3)
(9-3)
dove ![]() e c è il fattore di impacchettamento. Con l’utilizzo della legge di Lenz, trovo:
e c è il fattore di impacchettamento. Con l’utilizzo della legge di Lenz, trovo:
![]() (9-4)
(9-4)
da questa relazione si vede subito che, poiché la v(t) misurata non è esprimibile con la sopra scritta (9-4), nella valutazione della BM si commette un errore che è legato al fatto che si trascurano le armoniche di ordine superiore. L’espressione da noi utilizzata per il calcolo della Bm deriva, infatti, dalla seguente considerazione:
![]() (9-5)
(9-5)
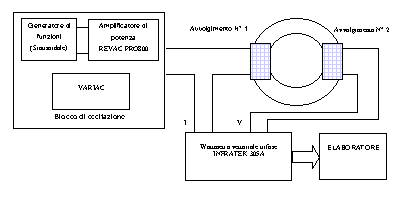
Figura 9-4. Schema di principio utilizzato per le misure in assenza di polarizzazione.
Un altro errore di stima è dovuto al fatto che il valore di campo magnetico da noi considerato non è quello effettivamente presente in ogni punto del toroide, ma quello che in realtà è presente solo su un valore particolare di raggio e che chiameremo Rm**. Dalla legge della circuitazione magnetica, trovo:
![]() dove
dove ![]() (9-6)
(9-6)
posso allora esprimere il flusso magnetico come:
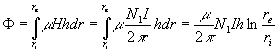 dove h è lo spessore del toroide (9-7)
dove h è lo spessore del toroide (9-7)
ma il flusso è anche esprimibile come:
![]() (9-8)
(9-8)
da cui, uguagliando la (9-8) e la (9-7), trovo:
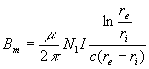 (9-9)
(9-9)
ricordando che ![]() , posso determinare l’espressione del campo magnetico:
, posso determinare l’espressione del campo magnetico:
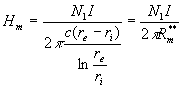 (9-10)
(9-10)
dalla relazione sopra scritta si ricava immediatamente il valore del raggio considerato Rm**.
Per la determinazione della permeabilità relativa del materiale, nello schema di figura 9-4 abbiamo utilizzato come blocco di eccitazione il variac in quanto in questo caso la frequenza richiesta per la misura era quella industriale a 50Hz, inoltre questo tipo di alimentazione garantiva una migliore sinusoidalità della corrente in uscita. Per effettuare la misura abbiamo poi eccitato il circuito con diversi valori di corrente, e quindi di campo magnetico, in modo da portare il materiale a lavorare con diversi valori di campo ed abbiamo rilevato, con l’ausilio di un elaboratore interfacciato con il wattmetro, varie grandezze allo scopo di determinare la curva di normale magnetizzazione del materiale e la permeabilità relativa.
Utilizzando le relazioni viste nel paragrafo precedente e con l’ausilio di un foglio elettronico, abbiamo determinato i valori di campo ed induzione per ogni valore di corrente di eccitazione. I risultati ottenuti sono riportati nel grafico di figura 9-5.
Per quanto riguarda la determinazione delle perdite nel materiale, lo schema di principio utilizzato per effettuare le misure è quello di figura 9-4. In questo caso ci siamo dovuti servire della coppia generatore di funzione-amplificatore in quanto la prova è stata effettuata a frequenza variabile. In particolare i valori di frequenza utilizzati sono stati: 10Hz, 20Hz, 30Hz, 40Hz, 50Hz, 60Hz, 70Hz, 80Hz, 90Hz e 100Hz. Per ogni valore di frequenza sono state misurate tensione, corrente e frequenza. Elaborando i dati delle misure abbiamo poi ricavato, per ogni valore di frequenza e con le approssimazioni viste nei paragrafi precedenti, i valori di campo, induzione, permeabilità e perdite nel materiale.
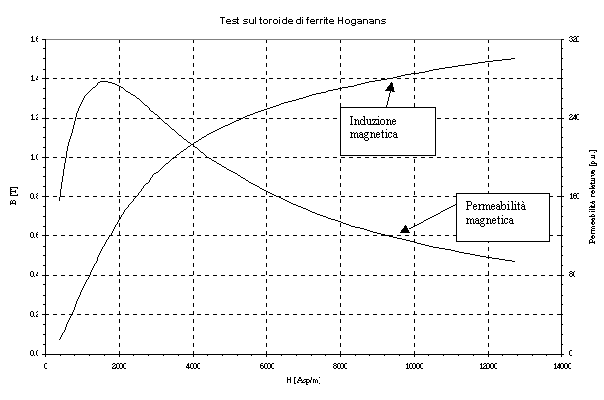
Figura 9-5. Andamento grafico della permeabilità e dell’induzione in funzione del campo magnetico, per il materiale in esame (Dati Sperimentali).
Abbiamo poi proceduto alla determinazione della cifra di perdita ed alla suddivisione delle perdite determinando, tramite opportuna ottimizzazione numerica, la quota di perdite da attribuire all’isteresi magnetica e quella da attribuire alle correnti parassite. Vediamo ora in dettaglio il procedimento per la determinazione della cifra di perdita. Consideriamo il nostro toroide e scriviamo l’equazione elettrica al circuito voltmetrico dell’avvolgimento 2,
![]() in quanto,
in quanto, ![]() (9-11)
(9-11)
ricordando, ora, la relazione che lega la f.e.m. indotta in un avvolgimento, percorso da una corrente sinusoidale, ed il flusso, abbiamo:
![]() (regime sinusoidale) (9-12)
(regime sinusoidale) (9-12)
e
![]() …..con:
…..con: ![]() (regime non sinusoidale). (9-13)
(regime non sinusoidale). (9-13)
Dalla definizione di cifra di perdita di un materiale, alla frequenza ![]() ,, facendo variare la
,, facendo variare la ![]() , diagrammo l’andamento delle perdite nel ferro (riferite all’unità di peso) in funzione dell’induzione max, e su tale curva per
, diagrammo l’andamento delle perdite nel ferro (riferite all’unità di peso) in funzione dell’induzione max, e su tale curva per ![]() vado a leggere il valore della cifra di perdita, la figura 9-6 mostra graficamente tale procedimento.
vado a leggere il valore della cifra di perdita, la figura 9-6 mostra graficamente tale procedimento.
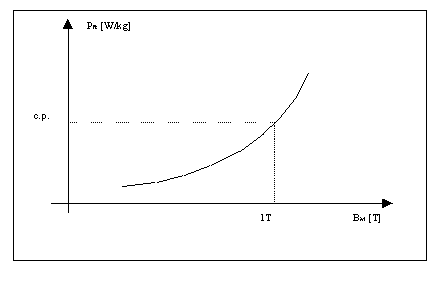
Figura 9-6. La figura illustra graficamente il procedimento da seguire per la determinazione della cifra di perdita.
Questo è il procedimento classico per la determinazione della cifra di perdita. Nel nostro caso, invece, la cifra di perdita è stata determinata a partire direttamente dai valori riportati nelle tabelle sopra citate, con l’ausilio di una funzione Visual Basic che non fa altro che individuare i due valori di campo entro cui si trova il valore, ![]() , e ricava il valore della cifra di perdita interpolando linearmente tra i due valori di potenza specifica ad essi associati. Riportiamo di seguito il listato Visual Basic di tale funzione.
, e ricava il valore della cifra di perdita interpolando linearmente tra i due valori di potenza specifica ad essi associati. Riportiamo di seguito il listato Visual Basic di tale funzione.
Function CifraDiPerdita(Indice_di_riga, N_colonne)
B1 = 0
B2 = 5
For i = 0 To N_colonne
If Range("E" & (Indice_di_riga + i)) > 0 Then
If (Range("D" & (Indice_di_riga + i)) > B1) And (Range("D" & (Indice_di_riga + i)) < 1) Then
Pfe1 = Range("E" & (Indice_di_riga + i))
B1 = Range("D" & (Indice_di_riga + i))
End If
If (Range("D" & (Indice_di_riga + i)) < B2) And (Range("D" & (Indice_di_riga + i)) > 1) Then
Pfe2 = Range("E" & (Indice_di_riga + i))
B2 = Range("D" & (Indice_di_riga + i))
End If
End If
Next i
CifraDiPerdita = InterLin(B1, Pfe1, B2, Pfe2, 1)
End Function
Riportiamo inoltre nella figura. 9-7 l’andamento grafico della cifra di perdita in funzione della frequenza.
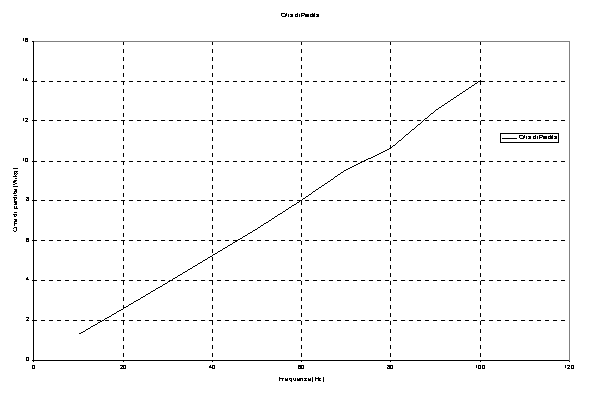
Figura 9-7. Andamento grafico della cifra di perdita, per il materiale studio, in funzione della frequenza.
Facciamo ora, come abbiamo già fatto per la determinazione della cifra di perdita, un discorso prima teorico e poi pratico per la separazione delle perdite. Fissato un certo valore di induzione, ad es. ![]() , faccio variare l’alimentazione a frequenza variabile, nota la relazione che esprime le perdite totali in un materiale ferromagnetico, e scrivendola come:
, faccio variare l’alimentazione a frequenza variabile, nota la relazione che esprime le perdite totali in un materiale ferromagnetico, e scrivendola come:
![]() (9-14)
(9-14)
trovo che su un piano (![]() ), tale relazione è l’equazione di una retta, la cui inclinazione rispetto all’asse delle
), tale relazione è l’equazione di una retta, la cui inclinazione rispetto all’asse delle ![]() , mi da l’
, mi da l’![]() . La figura 9-8 mostra graficamente quanto enunciato.
. La figura 9-8 mostra graficamente quanto enunciato.
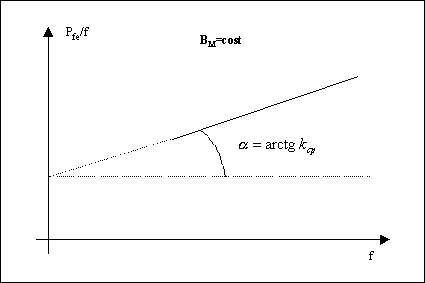
Figura 9-8. La figura illustra il procedimento da seguire per la separazione delle perdite.
Dalla curva ![]() , a
, a ![]() e per un certo valore di
e per un certo valore di ![]() , determino il valore delle perdite totali nel ferro, ed essendo noto
, determino il valore delle perdite totali nel ferro, ed essendo noto ![]() , determino il valore delle perdite per correnti parassite,
, determino il valore delle perdite per correnti parassite,
![]() da cui:
da cui: ![]() (9-15)
(9-15)
In questo modo ho separato le perdite per isteresi da quelle per correnti parassite, se voglio determinare anche il valore dell’esponente n delle perdite per isteresi, devo ripetere il procedimento visto sopra per altri valori di ![]() , ottenendo la curva
, ottenendo la curva ![]() per
per ![]() , ma poiché:
, ma poiché:
![]() , (9-16)
, (9-16)
che in coordinate logaritmiche mi da una retta, posso determinare l’esponente ![]() come l’arcotangente dell’angolo che tale retta forma con l’asse delle ascisse.
come l’arcotangente dell’angolo che tale retta forma con l’asse delle ascisse.
Nella nostra prova la separazione delle perdite non è stata fatta seguendo questo procedimento, ma utilizzando un metodo numerico (attraverso il risolutore di Excel).
Nella figura 9-9 è riportato l’andamento grafico delle perdite nel ferro in funzione del campo magnetico, mentre la figura 9-10 riporta le perdite nel ferro separate per isteresi e correnti parassite, inoltre in tabella 9-3 si riportano i valori trovati per i coefficienti ![]() ,
, ![]() ed
ed ![]() necessari per la separazione delle perdite.
necessari per la separazione delle perdite.
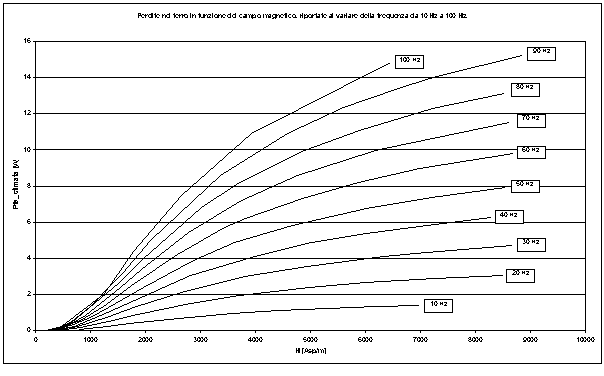
Figura 9-9. La figura mostra come variano le perdite nel ferro al variare del campo e della frequenza.

Tabella 9-3. Valori calcolati con procedimento numerico
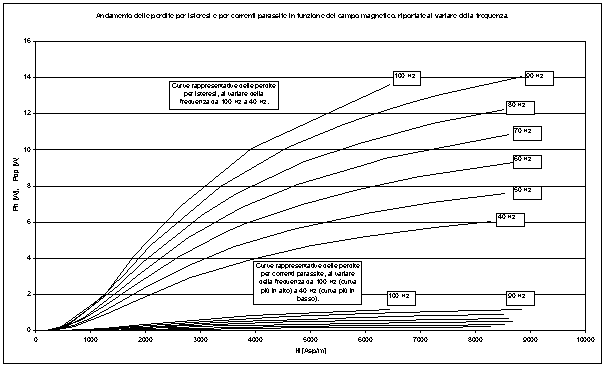
Figura 9-10. La figura mostra il contributo delle perdite per isteresi e per correnti parassite, al variare del campo e della frequenza, alle perdite totali nel ferro.
Dalle figure si vede subito che l’influenza maggiore sulle perdite totali nel ferro è data dalle perdite per isteresi. Questo era prevedibile, in quanto il materiale per come è fatto fisicamente non consente percorsi lunghi su cui possono richiudersi le correnti parassite.
9.6 Misura della permeabilità differenziale
Il secondo gruppo di misure effettuate sul provino, quelle più importanti ai fini del nostro studio, riguardano la determinazione della permeabilità differenziale.
Nei test in frequenza, come abbiamo visto, il motore era portato a lavorare in presenza della polarizzazione dovuta ai magneti con un segnale di eccitazione molto piccolo. In queste condizioni di lavoro non è esatto considerare nei calcoli la permeabilita normale del materiale, in quanto la presenza di polarizzazione porta il materiale a lavorare in un punto della caratteristica di normale magnetizzazione lontano dall’origine, ed inoltre in presenza di cicli d’isteresi molto ridotti. La figura 9-11 mostra graficamente tale concetto.
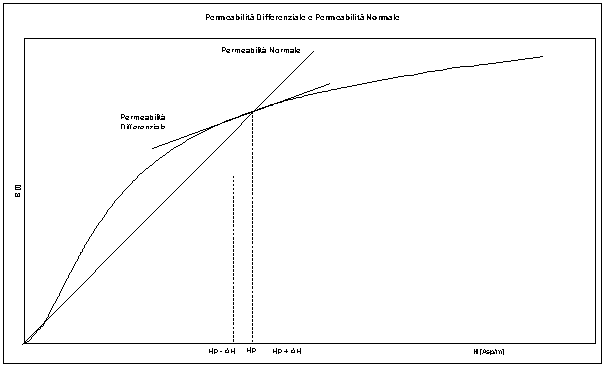
Figura 9-11. Effetto della polarizzazione del magnete sulla permeabilità del materiale in presenza di un piccolo segnale.
Dal grafico si vede chiaramente che la permeabilità differenziale del materiale in queste condizioni di lavoro risulta notevolmente più bassa della permeabilità normale.
In figura 9-12 è riportato lo schema di principio utilizzato per questa misura. Importante è sottolieare che per realizzare la polarizzazione necessaria alle misure si è dovuto ricorrere all’utilizzo di due alimentatori stabilizzati, in quanto il segnale di eccitazione contrastava tale polarizzazione.
Per determinare l’andamento della permeabilità differenziale si è calcolato il valore del ![]() dovuto all’eccitazione, noto il valore della corrente di polarizzazione si è calcolato il valore del campo di polarizzazione
dovuto all’eccitazione, noto il valore della corrente di polarizzazione si è calcolato il valore del campo di polarizzazione ![]() , la somma di questi due valori esprime il valore del campo a cui si riferisce la permeabilità differenziale che è calcolata come:
, la somma di questi due valori esprime il valore del campo a cui si riferisce la permeabilità differenziale che è calcolata come:
![]() (9-17)
(9-17)
In figura 9-13 è riportato l’anadamento grafico della permeabilità differenziale, calcolata per valori di campo prima crescenti e poi decrescenti, e l’andamento della permeablità normale.
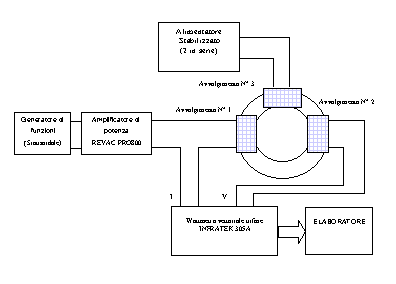
Figura 9-12. Schema di principio utilizzato per la misura della permeabilità differenziale.
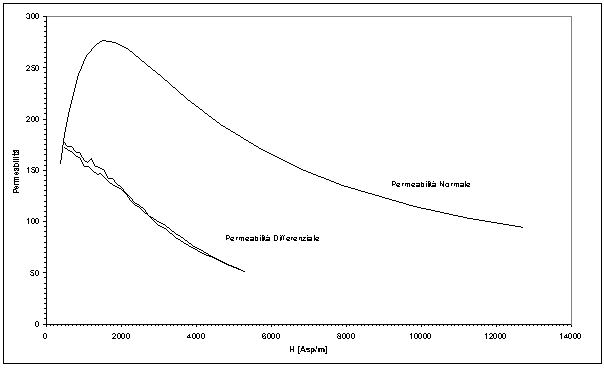
Figura 9-13. Andamento grafico della permeabilità differenziale e della permeabilità normale (Valori sperimentali).
Dalla figura 9-13 si vede chiaramente che i risultati sperimentali confermano quanto già osservato in modo teorico dall’analisi della figura 9-11. Questi risultati possono giustificare la discordanza dei risultati ottenuti con i test in frequenza, rispetto ai risultati ottenuti con le altre prove.
Analisi dei Risultati
10.1 Introduzione
In questo capitolo si cercherà di fare un’analisi critica dei risultati ottenuti nelle varie prove. Per quello che riguarda il modello in assi d e q della macchina, saranno chiariti i motivi dell’assenza dei circuiti smorzatori. Per quello che riguarda le misure, si procederà ad evidenziare i pregi ed i difetti delle varie prove effettuate per la determinazione dei parametri. Si cercheranno, inoltre, le cause che hanno portato nel caso dei test in frequenza a risultati diversi da quelli ottenuti nelle altre prove.
Lo scopo principale di questa tesi è la ricerca dei parametri del modello del motore AFIPM. Avendo a che fare con un motore a magneti permanenti, non è stato possibile utilizzare i metodi tradizionali per la ricerca dei parametri, in quanto non è possibile annullare il flusso di eccitazione. Inoltre, non avendo ancora a disposizione un sistema di controllo, non è stato possibile effettuare delle prove sul prototipo funzionante da motore. Si sono dovute, allora, effettuare delle prove a rotore bloccato, che purtroppo non rispecchiano le condizioni di alimentazione del funzionamento reale. Per questo motivo si è dovuto procedere ad ulteriori misure dei parametri ![]() ed
ed ![]() , facendo delle prove a carico.
, facendo delle prove a carico.
Essendo stati utilizzati, per la realizzazione del rotore del prototipo, materiali non convenzionali, è stato necessario procedere ad un’analisi preliminare volta alla individuazione del modello. Nel caso di macchine sincrone anisotrope a magneti permanenti, il modello generalmente adottato presenta uno o più rami smorzatori in parallelo all’induttanza di magnetizzazione, per tenere conto della presenza di correnti indotte nel ferro di rotore generate da funzionamenti asincroni o dalla presenza di armoniche sull’alimentazione.
Nel caso in esame si è visto (Capitolo 4), che nel circuito equivalente in assi d e q della macchina non sono presenti rami smorzatori. Ciò è dovuto alla scarsa circolazione di correnti indotte sul rotore, da attribuirsi all’utilizzo delle ferriti al posto dei tradizionali lamierini al ferro-silicio. Infatti, le ferriti essendo costituite da granuli di ferro elettricamente isolati, non consentono il passaggio della corrente da una particella all’altra. Ciò limita notevolmente la circolazione di correnti parassite e quindi l’influenza dei circuiti smorzatori sul modello della macchina. È utile ricordare, inoltre, che tali materiali sono indicati per l’utilizzo su nuclei magnetici per applicazioni in alta frequenza. Rimanendo sul tema delle ferriti, è interessante osservare come tale materiale allo stato attuale della tecnologia non è particolarmente indicato per l’impiego in applicazioni in bassa frequenza. Dai risultati emersi dalle misure fatte (Capitolo 9), è evidente che per applicazioni a frequenze industriali la cifra di perdita di tali materiali risulta ancora superiore a quella dei normali lamierini. Da notare, comunque, che la quasi totalità delle perdite è da attribuirsi all’isteresi magnetica, mentre l’influenza delle correnti parassite risulta assai ridotta.
Dopo aver motivato l’assenza dei circuiti smorzatori nel circuito equivalente della macchina, è importante chiarire quali problemi si sono incontrati nelle varie prove per la identificazione dei parametri. Cominciamo dalle prove effettuate a rotore bloccato.
Per quanto riguarda i test in frequenza (Capitolo 4), per arrivare alla determinazione dei parametri si è alimentata la macchina, prima in asse d e poi in asse q, con un segnale sinusoidale di piccola potenza nel campo di frequenze tra 10 mHz ed 1 kHz. Rilevando le forme d’onda di tensione e di corrente sugli avvolgimenti di statore della macchina, si è risaliti ai valori in modulo e fase dell’impedenza operazionale in funzione della frequenza. Per la determinazione dei parametri si è proceduto approssimando le curve misurate con quelle ottenute dalle equazioni del modello, variando i valori dei parametri ![]() ed
ed ![]() . Ottimizzando gli scarti tra le curve misurate e quelle calcolate si è risaliti ai valori dei parametri (
. Ottimizzando gli scarti tra le curve misurate e quelle calcolate si è risaliti ai valori dei parametri (![]() ed
ed ![]() ). Il limite nell’utilizzo di questo metodo, è legato al vincolo imposto dall’alimentazione. Essendo, infatti, richiesto un segnale sinusoidale su un ampio campo di frequenze e non avendo a disposizione generatori di potenza in grado di fornire, senza distorsioni, tali segnali si è vincolati all’utilizzo di segnali di piccola potenza. Questo comporta una sostanziale differenza tra il funzionamento reale della macchina e quello utilizzato per la determinazione dei parametri.
). Il limite nell’utilizzo di questo metodo, è legato al vincolo imposto dall’alimentazione. Essendo, infatti, richiesto un segnale sinusoidale su un ampio campo di frequenze e non avendo a disposizione generatori di potenza in grado di fornire, senza distorsioni, tali segnali si è vincolati all’utilizzo di segnali di piccola potenza. Questo comporta una sostanziale differenza tra il funzionamento reale della macchina e quello utilizzato per la determinazione dei parametri.
Cerchiamo di capire cosa cambia nella modellizzazione della macchina se si utilizzano segnali di piccola potenza. Durante il normale funzionamento della macchina, i materiali sono chiamati a lavorare con delle correnti notevoli, quindi sono sottoposti a cicli d’isteresi di non piccola ampiezza, ciò porta ad una lecita approssimazione della permeabilità del materiale con la permeabilità normale. In presenza di piccolo segnale ciò non è più vero, in quanto, avendo i cicli d’isteresi un’ampiezza ridotta, non è più possibile confondere la permeabilità del materiale con la permeabilità normale. Inoltre, la presenza dei magneti fa si che questi cicli d’isteresi siano polarizzati e quindi non più simmetrici rispetto all’origine. Per verificare il comportamento delle ferriti in presenza dei magneti e di un piccolo segnale di eccitazione, sono state condotte delle misure cercando di riprodurre le condizioni di lavoro del materiale all’interno del motore. I risultati di questa misura (Capitolo 9) hanno sostanzialmente confermato il diverso comportamento dei materiali in presenza di polarizzazione e di piccolo segnale. In particolare, si è verificato che la permeabilità differenziale è inferiore alla permeabilità normale anche per piccoli valori del campo di polarizzazione. Ricordando che tra induttanza e permeabilità c’è una relazione di diretta proporzionalità, si capisce perché i valori di induttanza in assi d e q trovati con questa prova risultano inferiori a quelli trovati con le altre prove.
Per avere una conferma della validità del modello, determinato con i test in frequenza, si è proceduto ad una verifica con delle prove nel tempo (Capitolo 5). Questa volta il motore è stato eccitato con correnti molto prossime a quelle che si hanno nel normale funzionamento. Per la determinazione dei parametri si è proceduto nel seguente modo: partendo dalla conoscenza del modello, della resistenza di fase degli avvolgimenti e del segnale di eccitazione, si sono ricercati i valori d’induttanza in assi d e q attraverso l’ottimizzazione, con il metodo dei minimi quadrati, delle equazioni del modello. Questa prova è stata condotta per cinque valori diversi di corrente; su ciascun asse i risultati ottenuti sono stati tutti coerenti tra loro. I valori medi ottenuti, con le diverse correnti, per le induttanze sui due assi sono: ![]() ed
ed ![]() .
.
Come già accennato all’inizio del paragrafo, non disponendo del controllo, per procedere alla determinazione dei parametri con la macchina in rotazione (Capitolo 6), è stato necessario far funzionare il prototipo come generatore sincrono a magneti permanenti trascinato in rotazione da un motore a corrente continua. Con tale generatore si sono alimentati due carichi diversi, uno puramente resistivo ed uno di tipo![]() . Per ogni tipo di carico sono state condotte sia prove a velocità costante, in cui si variava il carico per regolare la corrente, sia prove a velocità variabile in cui il carico era costante e si variava la velocità per regolare la corrente erogata. Per risalire ai parametri si è utilizzato il diagramma vettoriale della macchina. La parte più critica in questa prova è legata alla corretta valutazione dell’angolo di carico d . È noto che tale angolo è definito come la differenza di fase del vettore tensione sul carico ed il vettore f.e.m. a vuoto. Essendo, la tensione sul carico e la f.e.m. a vuoto, state ricavate in prove diverse, l’inconveniente maggiore era connesso alla esatta riproduzione della velocità di rotazione nelle prove a vuoto e a carico. Superato tale inconveniente, rimane il problema della stima dell’angolo d , in quanto la presenza di armoniche sulle forme d’onda campionate, non consente la determinazione di tale angolo come semplice differenza di fase tra gli attraversamenti a zero delle due forme d’onda campionate. Bisogna quindi determinare le fondamentali di tali forme d’onda, e poi risalire all’angolo d come differenza di fase tra gli attraversamenti a zero delle relative fondamentali. L’utilizzo del carico
. Per ogni tipo di carico sono state condotte sia prove a velocità costante, in cui si variava il carico per regolare la corrente, sia prove a velocità variabile in cui il carico era costante e si variava la velocità per regolare la corrente erogata. Per risalire ai parametri si è utilizzato il diagramma vettoriale della macchina. La parte più critica in questa prova è legata alla corretta valutazione dell’angolo di carico d . È noto che tale angolo è definito come la differenza di fase del vettore tensione sul carico ed il vettore f.e.m. a vuoto. Essendo, la tensione sul carico e la f.e.m. a vuoto, state ricavate in prove diverse, l’inconveniente maggiore era connesso alla esatta riproduzione della velocità di rotazione nelle prove a vuoto e a carico. Superato tale inconveniente, rimane il problema della stima dell’angolo d , in quanto la presenza di armoniche sulle forme d’onda campionate, non consente la determinazione di tale angolo come semplice differenza di fase tra gli attraversamenti a zero delle due forme d’onda campionate. Bisogna quindi determinare le fondamentali di tali forme d’onda, e poi risalire all’angolo d come differenza di fase tra gli attraversamenti a zero delle relative fondamentali. L’utilizzo del carico ![]() si è dimostrato poco adatto alla determinazione dei parametri, a causa dell’elevata sensitività dei parametri alla variazione dell’angolo di carico. Ciò in quanto, essendo in questo caso l’angolo di carico dell’ordine di pochi gradi, gli errori commessi nella determinazione di tale angolo, influenzano maggiormente la determinazione dei parametri. Per quanto riguarda, invece, la prova con carico puramente resistivo è possibile affermare che i risultati ottenuti (
si è dimostrato poco adatto alla determinazione dei parametri, a causa dell’elevata sensitività dei parametri alla variazione dell’angolo di carico. Ciò in quanto, essendo in questo caso l’angolo di carico dell’ordine di pochi gradi, gli errori commessi nella determinazione di tale angolo, influenzano maggiormente la determinazione dei parametri. Per quanto riguarda, invece, la prova con carico puramente resistivo è possibile affermare che i risultati ottenuti (![]() ed
ed ![]() ), confermano sostanzialmente i valori dei parametri determinati con i test nel tempo.
), confermano sostanzialmente i valori dei parametri determinati con i test nel tempo.
Dopo aver determinato i parametri della macchina, si è proceduto alla ricerca della caratteristica di coppia del motore (Capitolo 7). Questa misura è stata condotta a rotore bloccato alimentando il motore in continua. Iniettando nelle singole fasi del motore le tre componenti di un vettore corrente di modulo costante e facendo in modo che tale vettore ruotasse su tutti i 360 gradi elettrici, è possibile tracciare la caratteristica di coppia del motore. Ovviamente una misura di coppia fatta a motore fermo comporta notevoli problemi dovuti alla presenza degli attriti e della coppia di cogging. L’effetto di tali disturbi è difficilmente valutabile, in quanto le variabili che possono influenzare l’attrito sono molteplici, ciò costituisce un limite per tale tipo di prova. Per avere dei risultati attendibili, la caratteristica di coppia è stata stimata per sei valori diversi del modulo del vettore corrente, ed in due differenti posizioni del rotore. Per ognuna delle caratteristiche trovate si è risaliti al contributo dovuto alla prima armonica ed a quello dovuto alla seconda armonica (contributo di anisotropia). Ricordando la relazione che esprime la coppia in un motore sincrono anisotropo in un riferimento d-q sincrono con il rotore si è risaliti, con un’ottimizzazione ai minimi quadrati, ai valori dei parametri ![]() e
e ![]() . Questa prova ha confermato che la differenza
. Questa prova ha confermato che la differenza ![]() risulta sostanzialmente in linea con i valori trovati con le prove a carico e le prove nel tempo.
risulta sostanzialmente in linea con i valori trovati con le prove a carico e le prove nel tempo.
Restando sul tema della caratteristica di coppia, dopo aver determinato l’andamento in funzione dell’angolo di carico d , si è proceduto ad una stima, sia in termini di forma d’onda che in termini di ampiezza picco-picco, della coppia di cogging (Capitolo 8). Ruotando l’albero motore con incrementi angolari noti, si è misurata la coppia di cogging su un intervallo angolare di circa quattro passi di dentatura. Diagrammando i valori di coppia in funzione della posizione angolare, si è osservato che sulla coppia di cogging era sovrapposto un valore di coppia costante dovuta probabilmente agli attriti presenti. Per avere una conferma si è proceduto ad un’ulteriore misura della coppia di cogging partendo da una posizione angolare diversa. Questa volta, per ridurre l’effetto degli attriti dovuti alla presenza di un eventuale disassamento tra l’albero motore e l’albero su cui era montato il trasduttore di coppia, la prova è stata condotta con l’albero motore appena infilato nel manicotto di collegamento. Questa prova ha confermato l’andamento della forma d’onda del cogging e del suo valore picco-picco, ma il contributo degli attriti è stato visibilmente ridotto. Prendendo, quindi, le opportune precauzioni per ridurre l’influenza degli attriti, è possibile affermare che il metodo di misura utilizzato è idoneo per avere una stima della forma d’onda e dell’ampiezza picco-picco della coppia di cogging.
Ultima prova sperimentale cui vogliamo fare cenno, è il rilievo della forma d’onda di tensione prodotta dal motore nel funzionamento come generatore a vuoto (Capitolo 2). Con questa prova è stata fatta anche una stima delle perdite nel ferro e di quelle dovute agli attriti presenti nel normale funzionamento, nonché una stima del flusso concatenato con un avvolgimento di statore. Questa prova si è resa necessaria in quanto, si voleva confermare l’andamento della forma d’onda della f.e.m. a vuoto calcolata con l’Algoritmo di calcolo (Capitolo 3). I risultati ottenuti sono stati soddisfacenti, come dimostra la figura 10-1. La forma d’onda calcolata risulta leggermente più distorta di quella misurata sui fronti di salita e di discesa. Ciò è probabilmente dovuto al fatto che il programma di calcolo non tiene conto di effetti smorzanti (come ad esempio le correnti indotte nel ferro di statore), che in qualche misura tendono a limitare tale distorsione.
In conclusione si riporta in figura 10-2 il circuito equivalente della macchina in assi d e q, ed in tabella 10-1 i parametri trovati per il modello.
Come ulteriore sviluppo di questo lavoro è possibile pensare alla realizzazione del sistema di controllo, al fine di verificare il comportamento e le prestazioni dell’azionamento nel suo complesso. Per fare ciò i parametri calcolati con queste prove possono essere un valido punto di partenza, inoltre, avendo a disposizione il controllo sarà possibile effettuare ulteriori prove per la verifica dei parametri trovati. Per quello che riguarda l’algoritmo di calcolo, si potrà simulare il funzionamento a carico del motore e cercare di risalire ai parametri partendo dalla simulazione.
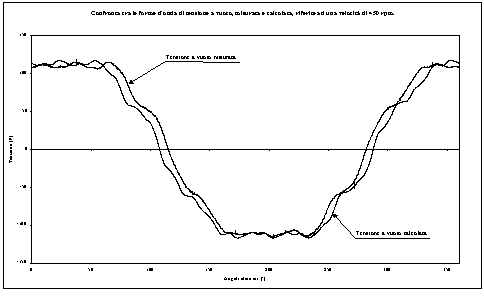
Figura 10-1. Confronto tra la f.e.m. a vuoto misurata e quella calcolata con l’Algoritmo.
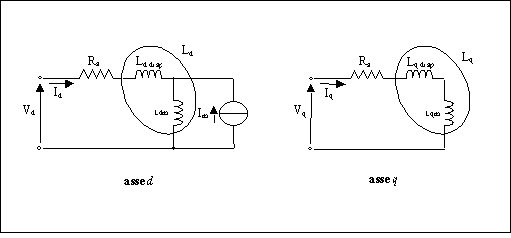
Figura 10-2. Circuito equivalente in assi d e q del prototipo AFIPM.

Tabella 10-1. Tabella riassuntiva dei parametri del motore determinati con le varie prove effettuate.
Trasformazioni di Variabili
A1.1 Introduzione
Per descrivere il funzionamento delle macchine elettriche rotanti in corrente alternata, vengono generalmente utilizzati sistemi di riferimento i cui assi coincidono con gli assi degli avvolgimenti. Rispetto a tali riferimenti sono poi descritte le varie funzioni, quali: distribuzione di conduttori, distribuzione di f.m.m. al traferro ecc. Considerando che le macchine elettriche hanno in genere tre o più avvolgimenti, è facile capire che la trattazione analitica del funzionamento diventa pesante.
Facendo uso delle trasformazioni di variabili, è possibile semplificare la trattazione analitica e rendere più semplice la comprensione dei principi alla base del funzionamento della macchina. Il vantaggio legato all’utilizzo di tali trasformazioni è quello di passare da una macchina più complessa la cui rappresentazione richiede un certo numero di equazioni, ad una equivalente a quella di partenza ma di più semplice modellizzazione, cioè descrivibile con un numero inferire di equazioni.
A1.2 Trasformazione trifase - bifase
Consideriamo un generico sistema di riferimento trifase i cui assi sono tra loro sfasati di 120 gradi. Si indichi con Xabc, tale sistema di riferimento. Si consideri, inoltre, un sistema di riferimento bifase ortogonale Xa b e si supponga che tale sistema di riferimento sia posizionato in modo che l’asse a del sistema Xabc, sia coincidente con l’asse a del sistema Xa b . La figura 1 illustra quanto detto.
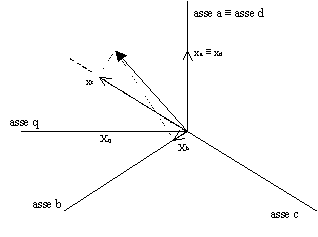
Figura 1. Rappresentazione di un vettore generico su un sistema di riferimenti trifase e su un sistema di riferimento bifase.
Le componenti del vettore rappresentato in figura 1, espresse nel sistema Xabc, possono essere espresse nel sistema Xa b , attraverso la seguente trasformazione:
![]() (1)
(1)
dove T è la matrice di trasformazione:
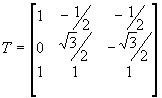 (2)
(2)
è importante osservare che la terza riga rappresenta l’eventuale componente omopolare presente nel sistema trifase.
Essendo T una matrice quadrata è possibile attraverso una trasformazione inversa passare dalle componenti nel sistema Xa b alle componenti nel sistema Xabc. Detta ![]() la matrice della trasformazione inversa, posso scrivere:
la matrice della trasformazione inversa, posso scrivere:
![]() dove, (3)
dove, (3)
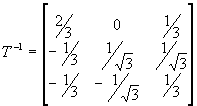
Questa trasformazione presenta, però, l’inconveniente di complicare l’espressione della potenza elettrica nel sistema Xa b . Ciò succede in quanto la matrice T non gode della proprietà di ortonormalità, cioè:
![]() (5)
(5)
Per evitare tale problema ed avere un’espressione della potenza invariata prima e dopo la trasformazione di variabili, si ricerca una matrice T0 che goda della proprietà di ortonormalità. Tale matrice è definita come:
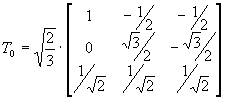 (6)
(6)
La trasformazione T0 espressa dalla (6), non altera il formalismo delle potenze nel cambio di sistema di riferimento, ed è la trasformazione utilizzata in questa tesi.
A1.3 Trasformazione di rotazione
La trasformazione di rotazione può essere utile, in alcuni casi, in quanto permette di trasformare grandezze in corrente alternata in grandezze in corrente continua.
Si consideri un generico sistema di riferimento Xdq, ruotato di un angolo J rispetto al sistema Xa b . La figura 2 mostra tali sistemi di riferimento.
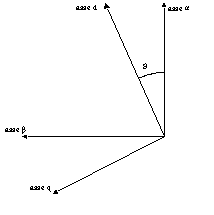
Figura 2. Sistemi di riferimento ruotati di un angolo J .
Dalla figura 2 è evidente che le coordinate di un generico vettore nel sistema Xa b , possono essere espresse nel sistema ruotato Xdq, mediante al relazione:
 (7)
(7)
L’inversa della matrice RJ si ottiene facilmente cambiando l’angolo J in -J .
Questa trasformazione conserva l’espressione della potenza, la matrice RJ risulta quindi ortonormale. Da notare che, se il sistema di riferimento Xdq ruota con una velocità istantanea ![]() rispetto al sistema Xa b , l’angolo J diventa una funzione del tempo esprimibile come l’integrale della velocità angolare istantanea.
rispetto al sistema Xa b , l’angolo J diventa una funzione del tempo esprimibile come l’integrale della velocità angolare istantanea.
A1.4 Considerazioni sulle trasformazioni di variabili
Si vogliono fare in questo paragrafo alcune osservazioni legate alle trasformazioni di variabili, nel caso di una macchina sincrona trifase a rotore avvolto.
Partendo dalla macchina trifase, utilizzando le trasformazioni di variabili, quale relazione intercorre tra i parametri della macchina di partenza e quelli della macchina bifase equivalente ?
Cominciamo col dire che la macchina bifase può essere ottenuta riavvolgendo in modalità bifase i circuiti di statore, rispettando il vincolo di utilizzare la stessa quantità di rame e di avere una macchina equivalente con la stessa potenza di quella trifase di partenza. Le caratteristiche della macchina dovranno, quindi, essere le seguenti:
rispetto ai conduttori della macchina trifase.
Con una macchina bifase equivalente fatta in questo modo, ci si aspetta che i parametri abbiano le seguenti caratteristiche.
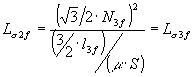 ;
;Determinazione dei Parametri:
Macchine a Campo Avvolto
A2.1 Introduzione
Si riporta, in questo appendice, una descrizione delle prove normalmente effettuate per la ricerca dei parametri nelle macchine a campo avvolto. Partiamo dalle equazioni della macchina, scritte con la convenzione di segno dei generatori per gli avvolgimenti di statore,
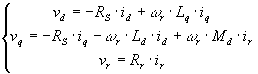 (1)
(1)
dove:
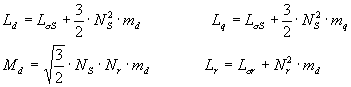 (2)
(2)
ed md ed mq sono dei coefficienti dipendenti dalla struttura geometrica della macchina.
In questa prova la macchina viene trascinata in rotazione ad una velocità nota w r da un motore primo. Per diversi valori della corrente di eccitazione si misura la f.e.m. a vuoto indotta sugli avvolgimenti di statore. Si ottiene così una curva affetta da saturazione, figura 1.
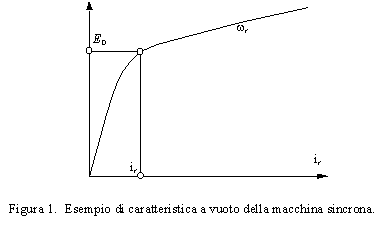
Il funzionamento della macchina in queste condizioni può essere descritto dalle (1), ponendo id = iq = 0. Noto il valore efficace di f.e.m. per un certo valore della ir, tenendo conto delle trasformazioni utilizzate, è possibile risalire al valore della Md (mutua induttanza tra statore e rotore), attraverso le seguenti relazioni:
![]() (3)
(3)
è importante osservare come questa prova sia fortemente influenzata dalla saturazione
In questa prova, portata la macchina in rotazione ad una certa velocità w r, si procede alla misura della corrente nelle fasi di statore, al variare della corrente di eccitazione.
La figura 2 riporta tale caratteristica.
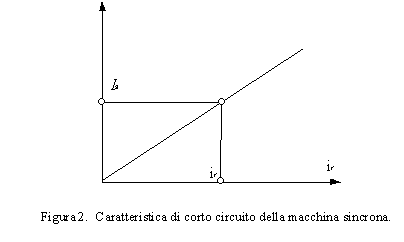
Il funzionamento della macchina in tale condizione può essere modellizzato ponendo nelle (1), vd = vq = 0. Se la resistenza di fase degli avvolgimenti di statore è piccola o la velocità w r è elevata, è possibile trascurare nelle prime due equazioni delle (1) il termine in cui compare la RS. Si ottiene, quindi, dalla prima delle (1) che iq = 0.
Noti i valori di Md, ir, id ed indicando con IS il valore efficace della corrente di cortocircuito di una fase, è possibile risalire tenendo conto delle trasformazioni usate al valore della induttanza sincrona in asse diretto. Quindi:
![]() (4)
(4)
In questa prova come si può vedere dalla figura 2, l’effetto della saturazione non è presente, infatti, la corrente di corto circuito tende a produrre un effetto magnetizzante opposto a quello prodotto dalla corrente di eccitazione, ciò elimina l’effetto della saturazione.
A2.4 Prova a corrente di armatura costante e cos
j = 0In questa prova la macchina sincrona viene portata al sincronismo attraverso un motore primo e connessa alla rete attraverso un autotrasformatore a rapporto variabile.
Regolando l'eccitazione della macchina e la coppia del motore primo, si fa in modo che la macchina scambi con la rete esclusivamente potenza reattiva. In queste condizioni si misurano i valori di corrente di eccitazione Ir1, di corrente di armatura Is1, e di tensione ai capi della macchina Vs1.
Tale misura viene ripetuta modificando la tensione ai capi della macchina sincrona variando il rapporto di trasformazione dell'autotrasformatore e si ritoccano conseguentemente i valori della corrente di eccitazione ed eventualmente della coppia del motore primo in modo che la corrente scambiata con la rete abbia lo stesso valore Is1 e sia ancora sfasata di 90° con la tensione. In queste condizioni si misurano i nuovi valori della corrente di eccitazione Ir2 e della tensione Vs2 ai capi della macchina. Ripetendo tale misura un certo numero di volte si ottiene una curva come quella riportata in figura 3.
Nell'ipotesi di poter trascurare le cadute di tensione resistive, il funzionamento della macchina può essere studiato con l’utilizzo delle seguenti equazioni:
![]() (5)
(5)
![]() (6)
(6)
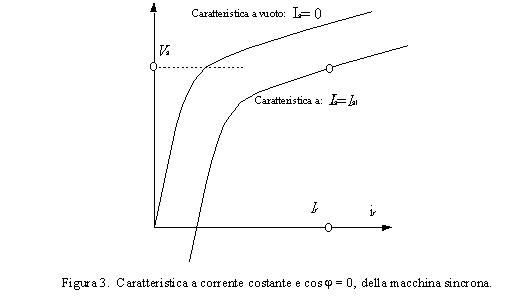
Nella (6), dividendo l'induttanza sincrona nella sua parte relativa alla dispersione e al flusso principale ed esplicitando in termini di numeri di spire i coefficienti induttivi, si arriva alle seguenti relazioni:
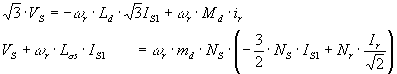 (7)
(7)
Il termine a primo membro indica la f.e.m. prodotta dalla macchina e dovuta al flusso di macchina realmente presente. Il termine a secondo membro, racchiuso dentro le parentesi tonde, rappresenta la f.m.m. risultante responsabile della produzione del flusso di macchina.
Indicando con E il valore efficace della f.e.m. e con Iecc_eq il valore di corrente di rotore che da solo produrrebbe a vuoto la f.e.m. E, si ottiene:
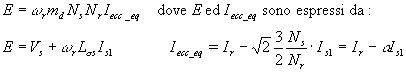 (8)
(8)
i valori di E ed Iecc_eq individuano dei punti sulla caratteristica a vuoto della macchina, mentre i corrispondenti punti della caratteristica a corrente di armatura costante e cos j = 0, risultano traslati di un vettore u, le cui componenti consentono di individuare sia a che Ls S.
Con a si è indicato il rapporto tra i numeri di spire equivalenti di statore e rotore.
A2.5 Misura della resistenza di fase
In genere la misura delle resistenze di fase è condotta con il metodo volt-amperometrico, per motori di potenza non troppo elevata. Per motori di potenza più elevata (superiore alla decina di kW), possono essere utilizzati metodi di maggiore precisione come i metodi di confronto.
La misura deve essere condotta a macchina in condizioni di riposo da un tempo sufficientemente lungo, per garantire che la temperatura degli avvolgimenti sia quella dell’ambiente circostante, ed inoltre deve essere condotta in tempi ridotti onde evitare far riscaldare gli avvolgimenti e quindi falsare la misura.
Tale misura deve essere condotta su tutte e tre le fasi, come valore di resistenza si considera la media dei valori ottenuti.
Listato dell’Algoritmo per il Calcolo
della Forma d’Onda della F.e.m. a Vuoto
In questa appendice è riportato il listato, Visual Basic per Excel, dell’Algoritmo descritto al capitolo 3.
***************************************************************************
Definizione delle costanti e delle variabili utilizzate nelle varie funzioni dell’Algoritmo.
***************************************************************************
Public Const pi_greco As Double = 3.141592654 ‘Costante
pPublic Const mu_zero = 4 * pi_greco * 0.0000001 ‘Permeabilità del vuoto
Public Const PaiaPoli As Single = 1 'N° di coppie polari della macchina equivalente
Public Const Ampiezza_fmm As Single = 551.21 'Ampiezza della fmm di rotore
Public Const N_Conduttori_Statore As Integer = 55 'Conduttori/Cava
Public Const N_Cave_macc_eq As Integer = 12 ‘Numero di cave della macchina equivalente
Public Const Apertura_cava_statore As Single = 0.0029 'IN METRI
Public Const Lung_traf_sr_min As Single = 0.001 'IN METRI
Public Const Lung_barr_flux As Single = 0.00205 'IN METRI
Public Leq_x(7) As Single 'Vettore che memorizza i 7 valori rappresentativi della
‘Lunghezza equivalente
Public H_x(7) As Single 'Vettore che memorizza i 7 valori rappresentativi della H(x)
Public x(7) As Single 'Vettore che memorizza i 7 valori rappresentativi della x
Public Lt_simm(15) As Single 'Vettore che memorizza i 15 valori rappresentativi
‘della Lt equivalente simmetrica
Public xt(15) As Single 'Vettore che memorizza i 15 valori rappresentativi della
‘coordinata di traferro x simmetrica cui si riferisce la Lt
‘Vari vettori necessari per la suddivisione della macchina
‘in corone circolari per il calcolo del flusso
Public Lung_tegolo(1000) As Double
Public Lung_polo_disp(1000) As Double
Public R1(1000) As Double
Public R2(1000) As Double
Public f1(999) As Double
Public f2(999) As Double
Public R1m(999) As Double
Public R2m(999) As Double
Public delta_teta(999) As Double
Public N_settori As Integer
Public Elem_vett_alfa As Integer
Public Incr_vett_alfa As Single
Public Elem_vett_teta As Integer
Public Incr_vett_teta As Single
Public Flux As Double
Public ang2 As Double
Public ang3 As Double
Public a(0 To 3600) As Double ' N.B. Il minimo incremento di angolo possibile
Public ls(0 To 3600) As Double ' è 0,1 gradi elettrici
Public lr(0 To 3600) As Double ' Questo è legato al fatto di aver definito
Public N1(0 To 3600) As Double ' i vettori con soli 3600 elementi
Public N2(0 To 3600) As Double
Public N3(0 To 3600) As Double
***************************************************************************
Definizione di alcune funzioni elementari utilizzate dalle Funzioni dell’Algoritmo.
***************************************************************************
'Definizione di una funzione che fa l'interpolazione lineare tra due punti A(xa,ya) e B(xb,yb)
'Si considera un triangolo rettangolo di vertici A, B, C(angolo retto), dove:
'AC è la base, e BC è 'altezza
Public Function InterLin(xa, ya, xb, yb, x_pto_incognito)
InterLin = (((x_pto_incognito - xa) * (yb - ya)) / (xb - xa)) + ya
End Function
'Definizione della funzione che fa il riporto di un angolo qualunque all'angolo "teta"
'Vengono fatti i riporti anche per gli angoli negativi "FUNZIONE PARI"
Public Function RipTeta(angolo, teta)
If angolo < 0 Then angolo = -angolo
While angolo > teta
angolo = angolo - teta
Wend
RipTeta = angolo
End Function
'La funzione fa il riporto in gradi elettrici di grandezze della macchina espresse in METRI
Public Function Rip_m_grad_elt(lung_circ_m, grand_da_trasf)
Rip_m_grad_elt = (360 * grand_da_trasf) / lung_circ_m
End Function
***************************************************************************
Routine che calcola la lunghezza equivalente magnetica in prossimità di una cava.
***************************************************************************
'Quaesta procedura crea due vettori Lt_simm ed xt (di 16 elementi) che contengono rispettivamente
'la lunghezza equivalente di traferro e la coordinata x spaziale ad essa corrispondente
'Questa funzione tiene conto che la lunghezza equivalente di traferro non è costante
'Se la ROUTINE viene chiamata con il perimetro della macchina equivalente Coppie_Polari deve
'essere impostato a 1 se il perimetro è quello della macchina reale Coppie_Polari deve essere
'uguale al numero di coppie polari della macchina reale
Public Sub crea_vettore(Diff_Pot_Magnetico, Apertura_Cava, Spessore_Traf, Coppie_Polari, perimetro_m)
c1 = Apertura_Cava / (2 * Spessore_Traf)
c2 = (2 * c1 * Spessore_Traf) / pi_greco
c3 = 1 / (2 * c1 * Log(10#))
Hmax = Diff_Pot_Magnetico / Spessore_Traf
For i = 0 To 7 Step 1
Select Case i
Case 0
w = 0
Case 1
w = 0.2
Case 2
w = 0.4
Case 3
w = 0.7
Case 4
w = 0.9
Case 5
w = 0.96
Case 6
w = 0.99
Case 7
w = 0.999
End Select
H_x(i) = Hmax * (1 / Sqr(1 + c1 ^ 2 * (1 - w ^ 2)))
c4 = Sqr(1 + c1 ^ 2 * (1 - w ^ 2))
c5 = (c1 * w / (Sqr(1 + c1 ^ 2)))
x(i) = c2 * (Atn(c5 / Sqr(-c5 * c5 + 1)) + c3 * Log((c4 + w) / (c4 - w)))
Leq_x(i) = (Hmax * Spessore_Traf) / H_x(i)
Next
For j = 0 To 7
Lt_simm(j) = Leq_x(7 - j)
xt(j) = Coppie_Polari * ((-x(7 - j) + x(7))) * 360 / perimetro_m
Next
For j = 8 To 15
Lt_simm(j) = Leq_x(j - 8)
xt(j) = Coppie_Polari * ((x(j - 8) + x(7)) * 360) / perimetro_m
Next
End Sub
***************************************************************************
Funzione f.m.m di rotore al traferro (Paragrafo 3.5).
***************************************************************************
'La funzione Ar descrive la distribuzione di fmm generata dai magneti del rotore
'note le grandezze geometriche della macchina e l'ampiezza della fmm (Ampiezza_fmm)
'La macchina considerata presenta due tegoli a copertura dei magneti, due poli di dispersione
'e quattro barriere di flusso. Il periodo elettrico della funzione è 360°
'I parametri rappresentativi di grandezze meccaniche (lunghezze) vanno espressi in mm
Public Function Ar(Lung_tegolo, Lung_polo_disp, Lung_barr_flux, angolo_elt)
If angolo_elt < 0 Then angolo_elt = -angolo_elt
Const d = 0.00000001 'Serve a descrivere il minore nell'istruzione Case
'Calcolo del perimetro
perimetro_macc_eq = 2 * (Lung_tegolo + Lung_polo_disp) + 4 * Lung_barr_flux
'Conversione delle grandezze da m a gradi elettrici
tegolo_elt = Rip_m_grad_elt(perimetro_macc_eq, Lung_tegolo)
polo_disp_elt = Rip_m_grad_elt(perimetro_macc_eq, Lung_polo_disp)
barr_flux_elt = Rip_m_grad_elt(perimetro_macc_eq, Lung_barr_flux)
a1 = tegolo_elt / 2 '- delta_angolo
a2 = a1 + barr_flux_elt
a3 = a2 + polo_disp_elt 'Calcolo dei punti necessari alla rappresentazione
a4 = a3 + barr_flux_elt 'della funzione
a5 = a4 + tegolo_elt
a6 = a5 + barr_flux_elt
a7 = a6 + polo_disp_elt
a8 = a7 + barr_flux_elt
a9 = a8 + a1 '+ 2 * delta_angolo
If angolo_elt > 360 Then angolo_elt = RipTeta(angolo_elt, 360) 'Riporto dell'angolo a 360° elt
Select Case angolo_elt 'Calcolo della funzione
Case 0 To a1 - d
Ar = Ampiezza_fmm
Case a1 To a2
Ar = InterLin(a2, 0, a1, Ampiezza_fmm, angolo_elt)
Case a2 - d To a3 - d
Ar = 0
Case a3 To a4
Ar = InterLin(a3, 0, a4, -Ampiezza_fmm, angolo_elt)
Case a4 - d To a5 - d
Ar = -Ampiezza_fmm
Case a5 To a6
Ar = InterLin(a6, 0, a5, -Ampiezza_fmm, angolo_elt)
Case a6 - d To a7 - d
Ar = 0
Case a7 To a8
Ar = InterLin(a8, Ampiezza_fmm, a7, 0, angolo_elt)
Case a8 - d To 360
Ar = Ampiezza_fmm
End Select
End Function
***************************************************************************
Funzione lunghezza di traferro vista da un osservatore solidale con il rotore
(Paragrafo 3.3).
***************************************************************************
Public Function lt_s(N_Cave_macc_eq, Lung_tegolo, Lung_polo_disp, Lung_barr_flux, angolo_elt)
If angolo_elt < 0 Then angolo_elt = -angolo_elt
Const d = 0.00000001 'Serve a descrivere il minore nell'istruzione Case
'Calcolo del perimetro
perimetro_macc_eq = 2 * (Lung_tegolo + Lung_polo_disp) + 4 * Lung_barr_flux
Call crea_vettore(Ampiezza_fmm, Apertura_cava_statore, Lung_traf_sr_min, PaiaPoli, perimetro_macc_eq)
‘Determina l'ampiezza in gradi elettrici di una coppia dente-cava della macchina equivalente bipolare
cava_dente_gra_elt = 360 / N_Cave_macc_eq
a1 = (cava_dente_gra_elt - xt(15)) / 2 'Inizio della perturbazione dovuta alla cava
If angolo_elt > cava_dente_gra_elt Then angolo_elt = RipTeta(angolo_elt, cava_dente_gra_elt)
Select Case angolo_elt
Case 0 To a1 - d
lt_s = Lung_traf_sr_min
Case a1 + xt(0) To a1 + xt(1) - d
lt_s = InterLin(a1 + xt(0), Lt_simm(0), a1 + xt(1), Lt_simm(1), angolo_elt)
Case a1 + xt(1) To a1 + xt(2) - d
lt_s = InterLin(a1 + xt(1), Lt_simm(1), a1 + xt(2), Lt_simm(2), angolo_elt)
Case a1 + xt(2) To a1 + xt(3) - d
lt_s = InterLin(a1 + xt(2), Lt_simm(2), a1 + xt(3), Lt_simm(3), angolo_elt)
Case a1 + xt(3) To a1 + xt(4) - d
lt_s = InterLin(a1 + xt(3), Lt_simm(3), a1 + xt(4), Lt_simm(4), angolo_elt)
Case a1 + xt(4) To a1 + xt(5) - d
lt_s = InterLin(a1 + xt(4), Lt_simm(4), a1 + xt(5), Lt_simm(5), angolo_elt)
Case a1 + xt(5) To a1 + xt(6) - d
lt_s = InterLin(a1 + xt(5), Lt_simm(5), a1 + xt(6), Lt_simm(6), angolo_elt)
Case a1 + xt(6) To a1 + xt(7) - d
lt_s = InterLin(a1 + xt(6), Lt_simm(6), a1 + xt(7), Lt_simm(7), angolo_elt)
Case a1 + xt(8) To a1 + xt(9) - d
lt_s = InterLin(a1 + xt(9), Lt_simm(9), a1 + xt(8), Lt_simm(8), angolo_elt)
Case a1 + xt(9) To a1 + xt(10) - d
lt_s = InterLin(a1 + xt(10), Lt_simm(10), a1 + xt(9), Lt_simm(9), angolo_elt)
Case a1 + xt(10) To a1 + xt(11) - d
lt_s = InterLin(a1 + xt(11), Lt_simm(11), a1 + xt(10), Lt_simm(10), angolo_elt)
Case a1 + xt(11) To a1 + xt(12) - d
lt_s = InterLin(a1 + xt(12), Lt_simm(12), a1 + xt(11), Lt_simm(11), angolo_elt)
Case a1 + xt(12) To a1 + xt(13) - d
lt_s = InterLin(a1 + xt(13), Lt_simm(13), a1 + xt(12), Lt_simm(12), angolo_elt)
Case a1 + xt(13) To a1 + xt(14) - d
lt_s = InterLin(a1 + xt(14), Lt_simm(14), a1 + xt(13), Lt_simm(13), angolo_elt)
Case a1 + xt(14) To a1 + xt(15) - d
lt_s = InterLin(a1 + xt(15), Lt_simm(15), a1 + xt(14), Lt_simm(14), angolo_elt)
Case a1 + xt(15) To cava_dente_gra_elt
lt_s = Lung_traf_sr_min
End Select
End Function
***************************************************************************
Funzione lunghezza di traferro vista da un osservatore solidale con lo statore
(Paragrafo 3.4).
***************************************************************************
Public Function lt_r(Lung_tegolo, Lung_polo_disp, Lung_barr_flux, angolo_elt)
If angolo_elt < 0 Then angolo_elt = -angolo_elt
Const d = 0.00000001 'Serve a descrivere il minore nell'istruzione Case
'Calcolo del perimetro
perimetro_macc_eq = 2 * (Lung_tegolo + Lung_polo_disp) + 4 * Lung_barr_flux
'Conversione delle grandezze da mm a gradi elettrici
tegolo_elt = Rip_m_grad_elt(perimetro_macc_eq, Lung_tegolo)
polo_disp_elt = Rip_m_grad_elt(perimetro_macc_eq, Lung_polo_disp)
barr_flux_elt = Rip_m_grad_elt(perimetro_macc_eq, Lung_barr_flux)
Call crea_vettore(Ampiezza_fmm, Lung_barr_flux, Lung_traf_sr_min, PaiaPoli, perimetro_macc_eq)
'Questa funzione ha un periodo di 180 gradi elettrici
If angolo_elt > 180 Then angolo_elt = RipTeta(angolo_elt, 180)
'Allungamento virtuale della cava
b1 = (xt(15) - barr_flux_elt) / 2
b2 = tegolo_elt / 2 - b1
b3 = b2 + xt(15) + polo_disp_elt - b1
Select Case angolo_elt
Case 0 To b2 - d
lt_r = Lung_traf_sr_min
Case b2 + xt(0) To b2 + xt(1) - d
lt_r = InterLin(b2 + xt(0), Lt_simm(0), b2 + xt(1), Lt_simm(1), angolo_elt)
Case b2 + xt(1) To b2 + xt(2) - d
lt_r = InterLin(b2 + xt(1), Lt_simm(1), b2 + xt(2), Lt_simm(2), angolo_elt)
Case b2 + xt(2) To b2 + xt(3) - d
lt_r = InterLin(b2 + xt(2), Lt_simm(2), b2 + xt(3), Lt_simm(3), angolo_elt)
Case b2 + xt(3) To b2 + xt(4) - d
lt_r = InterLin(b2 + xt(3), Lt_simm(3), b2 + xt(4), Lt_simm(4), angolo_elt)
Case b2 + xt(4) To b2 + xt(5) - d
lt_r = InterLin(b2 + xt(4), Lt_simm(4), b2 + xt(5), Lt_simm(5), angolo_elt)
Case b2 + xt(5) To b2 + xt(6) - d
lt_r = InterLin(b2 + xt(5), Lt_simm(5), b2 + xt(6), Lt_simm(6), angolo_elt)
Case b2 + xt(6) To b2 + xt(7) - d
lt_r = InterLin(b2 + xt(6), Lt_simm(6), b2 + xt(7), Lt_simm(7), angolo_elt)
Case b2 + xt(8) To b2 + xt(9) - d
lt_r = InterLin(b2 + xt(9), Lt_simm(9), b2 + xt(8), Lt_simm(8), angolo_elt)
Case b2 + xt(9) To b2 + xt(10) - d
lt_r = InterLin(b2 + xt(10), Lt_simm(10), b2 + xt(9), Lt_simm(9), angolo_elt)
Case b2 + xt(10) To b2 + xt(11) - d
lt_r = InterLin(b2 + xt(11), Lt_simm(11), b2 + xt(10), Lt_simm(10), angolo_elt)
Case b2 + xt(11) To b2 + xt(12) - d
lt_r = InterLin(b2 + xt(12), Lt_simm(12), b2 + xt(11), Lt_simm(11), angolo_elt)
Case b2 + xt(12) To b2 + xt(13) - d
lt_r = InterLin(b2 + xt(13), Lt_simm(13), b2 + xt(12), Lt_simm(12), angolo_elt)
Case b2 + xt(13) To b2 + xt(14) - d
lt_r = InterLin(b2 + xt(14), Lt_simm(14), b2 + xt(13), Lt_simm(13), angolo_elt)
Case b2 + xt(14) To b2 + xt(15) - d
lt_r = InterLin(b2 + xt(15), Lt_simm(15), b2 + xt(14), Lt_simm(14), angolo_elt)
Case b2 + xt(15) To b3 - d
lt_r = Lung_traf_sr_min
Case b3 + xt(0) To b3 + xt(1) - d
lt_r = InterLin(b3 + xt(0), Lt_simm(0), b3 + xt(1), Lt_simm(1), angolo_elt)
Case b3 + xt(1) To b3 + xt(2) - d
lt_r = InterLin(b3 + xt(1), Lt_simm(1), b3 + xt(2), Lt_simm(2), angolo_elt)
Case b3 + xt(2) To b3 + xt(3) - d
lt_r = InterLin(b3 + xt(2), Lt_simm(2), b3 + xt(3), Lt_simm(3), angolo_elt)
Case b3 + xt(3) To b3 + xt(4) - d
lt_r = InterLin(b3 + xt(3), Lt_simm(3), b3 + xt(4), Lt_simm(4), angolo_elt)
Case b3 + xt(4) To b3 + xt(5) - d
lt_r = InterLin(b3 + xt(4), Lt_simm(4), b3 + xt(5), Lt_simm(5), angolo_elt)
Case b3 + xt(5) To b3 + xt(6) - d
lt_r = InterLin(b3 + xt(5), Lt_simm(5), b3 + xt(6), Lt_simm(6), angolo_elt)
Case b3 + xt(6) To b3 + xt(7) - d
lt_r = InterLin(b3 + xt(6), Lt_simm(6), b3 + xt(7), Lt_simm(7), angolo_elt)
Case b3 + xt(8) To b3 + xt(9) - d
lt_r = InterLin(b3 + xt(9), Lt_simm(9), b3 + xt(8), Lt_simm(8), angolo_elt)
Case b3 + xt(9) To b3 + xt(10) - d
lt_r = InterLin(b3 + xt(10), Lt_simm(10), b3 + xt(9), Lt_simm(9), angolo_elt)
Case b3 + xt(10) To b3 + xt(11) - d
lt_r = InterLin(b3 + xt(11), Lt_simm(11), b3 + xt(10), Lt_simm(10), angolo_elt)
Case b3 + xt(11) To b3 + xt(12) - d
lt_r = InterLin(b3 + xt(12), Lt_simm(12), b3 + xt(11), Lt_simm(11), angolo_elt)
Case b3 + xt(12) To b3 + xt(13) - d
lt_r = InterLin(b3 + xt(13), Lt_simm(13), b3 + xt(12), Lt_simm(12), angolo_elt)
Case b3 + xt(13) To b3 + xt(14) - d
lt_r = InterLin(b3 + xt(14), Lt_simm(14), b3 + xt(13), Lt_simm(13), angolo_elt)
Case b3 + xt(14) To b3 + xt(15) - d
lt_r = InterLin(b3 + xt(15), Lt_simm(15), b3 + xt(14), Lt_simm(14), angolo_elt)
Case b3 + xt(15) To 180
lt_r = Lung_traf_sr_min
End Select
End Function
***************************************************************************
Funzione distribuzione di conduttori (Paragrafo 3.2).
***************************************************************************
'Definizione di una funzione che restituisce il numero di conduttori
'di una fase di statore in un punto
Public Function Ns(alfa)
If alfa < 0 Then alfa = -alfa
If alfa > 360 Then alfa = RipTeta(alfa, 360) 'Questa funzione è periodica di 360° elettrici
If ((alfa >= 0) And (alfa < 15) Or (alfa >= 345) And (alfa < 360) Or (alfa >= 165) And (alfa < 195)) _
Then Ns = 0 Else _
If (alfa >= 15) And (alfa < 165) _
Then Ns = N_Conduttori_Statore Else _
If (alfa >= 195) And (alfa < 345) _
Then Ns = -N_Conduttori_Statore
End Function
***************************************************************************
Funzione che calcola la lunghezza del polo principale, del polo di dispersione e delle barriere di flusso in funzione del raggio.
***************************************************************************
'Questa funzione calcola la lunghezza del Tegolo e del Polo di Dispersione ai vari raggi.
'Il parametro (a) passato alla funzione indica il raggio come frazione del settore circolare.
'I valori delle lunghezze restituiti dalla funzione sono in metri.
Sub Calcola_lunghezze(a As Integer)
Const Xn As Double = 39.823
Const Yn As Double = 30.234
Const Xm As Double = 75.999
Const Ym As Double = 72.451
Const Xe As Double = 49.964
Const Ye As Double = 1.883
Const Xf As Double = 102.864
Const Yf As Double = 21.071
Dim X1a(1000) As Double
Dim X2a(1000) As Double
Dim Y1a(1000) As Double
Dim Y2a(1000) As Double
inc_X1a = (Xm - Xn) / a
inc_Y1a = (Ym - Yn) / a
inc_X2a = (Xf - Xe) / a
inc_Y2a = (Yf - Ye) / a
For i = 0 To a
Select Case i
Case 0
X1a(i) = Xn
Y1a(i) = Yn
X2a(i) = Xe
Y2a(i) = Ye
R1(i) = Sqr(X1a(i) ^ 2 + Y1a(i) ^ 2) * 0.001
R2(i) = Sqr(X2a(i) ^ 2 + Y2a(i) ^ 2) * 0.001
Case 1 To a
X1a(i) = X1a(i - 1) + inc_X1a
Y1a(i) = Y1a(i - 1) + inc_Y1a
X2a(i) = X2a(i - 1) + inc_X2a
Y2a(i) = Y2a(i - 1) + inc_Y2a
R1(i) = Sqr(X1a(i) ^ 2 + Y1a(i) ^ 2) * 0.001
R1m(i - 1) = Sqr(((X1a(i) + X1a(i - 1)) / 2) ^ 2 + ((Y1a(i) + Y1a(i - 1)) / 2) ^ 2) * 0.001
R2(i) = Sqr(X2a(i) ^ 2 + Y2a(i) ^ 2) * 0.001
R2m(i - 1) = Sqr(((X2a(i) + X2a(i - 1)) / 2) ^ 2 + ((Y2a(i) + Y2a(i - 1)) / 2) ^ 2) * 0.001
f1(i - 1) = Atn((Y1a(i) + Y1a(i - 1)) / (X1a(i) + X1a(i - 1)))
f1(i - 1) = (360 * f1(i - 1)) / (2 * pi_greco)
f2(i - 1) = Atn((Y2a(i) + Y2a(i - 1)) / (X2a(i) + X2a(i - 1)))
f2(i - 1) = (360 * f2(i - 1)) / (2 * pi_greco)
delta_teta(i - 1) = ((((f1(i - 1) - f2(i - 1)) / 2) + f2(i - 1)) - (f1(0) - f2(0)) / 2 - f2(0)) * 4
End Select
Next i
For i = 0 To a - 1
Circ = (2 * pi_greco * (R1m(i) + R2m(i)) / 2)
Lung_tegolo(i) = Circ / 360 * (f1(i) - f2(i))
Lung_polo_disp(i) = ((Circ - (16 * Lung_barr_flux + 8 * Lung_tegolo(i))) / 8)
Next i
End Sub
***************************************************************************
Parte principale del programma, dove vengono calcolati e memorizzati nei rispettivi vettori i valori delle varie routine in funzione dell’angolo. Il tale routine vengono calcolati anche i flussi concatenati con gli avvolgimenti.
***************************************************************************
'Le grandezze meccaniche vanno espresse in metri
'Rx raggio considerato per la misura
'Re raggio esterno del settore considerato
'Ri raggio interno del settore considerato
'Cell è il numero relativo alla colonna in cui devo visualizzare il flusso
Sub Inizializza_Vettori(Lung_tegolo, Lung_polo_disp, Re, Ri, delta_ang, Cell)
Elem_vett_alfa = 360 / Incr_vett_alfa
Elem_vett_teta = 360 / Incr_vett_teta
delta_ang = Int(delta_ang * 10) 'Devo impostare sempre Incr_vett_alfa=0,1
For i = 0 To Elem_vett_alfa
'IMPORTANTE
'Devo sempre passare ang2 come parametro alle funzioni, perchè durante l'esecuzione
'del codice le funzioni chiamate modificano l'angolo passato come parametro (ang3)
'Evidentemente Visual Basic passa come parametri alle funzioni l'indirizzo
'delle variabili e non il valore (copia)
ang2 = i * Incr_vett_alfa
ang1 = i * Incr_vett_teta
ang3 = ang2
a(i) = Ar(Lung_tegolo, Lung_polo_disp, Lung_barr_flux, ang3)
ang3 = ang2
ls(i) = lt_s(N_Cave_macc_eq, Lung_tegolo, Lung_polo_disp, Lung_barr_flux, ang3)
ang3 = ang2
lr(i) = lt_r(Lung_tegolo, Lung_polo_disp, Lung_barr_flux, ang3)
ang3 = ang2
N1(i) = Ns(ang3)
ang3 = ang2
N2(i) = Ns(ang3 + 120)
ang3 = ang2
N3(i) = Ns(ang3 + 240)
Cells(i + 7, 1).Value = ang2
Cells(i + 7, 2).Value = ang1
Cells(i + 7, 3).Value = a(i)
Cells(i + 7, 4).Value = ls(i)
Cells(i + 7, 5).Value = lr(i)
Cells(i + 7, 6).Value = N1(i)
Cells(i + 7, 7).Value = N2(i)
Cells(i + 7, 8).Value = N3(i)
Next i
For j = 0 To Elem_vett_teta
Flux = 0
For k = 0 To Elem_vett_alfa
teta = j '* ((Elem_vett_alfa) / (Elem_vett_teta))
ang4 = k - teta - delta_ang
alfa = k
If (ang4 < 0) Or (ang4 > Elem_vett_alfa) Then ang4 = RipTeta(ang4, Elem_vett_alfa)
fluxN = a(ang4) * N1(alfa)
FluxD = ls(alfa) + lr(ang4) - Lung_traf_sr_min
Flux = (fluxN / FluxD) * Incr_vett_alfa + Flux
Next k
Flux = Flux * mu_zero * ((Re + Ri) / 2) * (Re - Ri)
Cells(j + 7, Cell).Value = Flux
Next j
End Sub
***************************************************************************
Ruotine principale (da chiamare per eseguire l’Algoritmo), in cui viene inizializzato il foglio Excel "Foglio di Calcolo". Tale routine, esegue il calcolo della forma d’onda della f.e.m. a vuoto in funzione della velocità di rotazione.
Nella scelta del numero di settori, in cui dividere la macchina, si consideri che il tempo di calcolo del flusso concatenato in ogni settore richiede circa 4 minuti con gli attuali sistemi di elaborazione.
***************************************************************************
Sub Start()
'Cancella il contenuto del foglio
Worksheets("Foglio di Calcolo").Activate
Range("A1:T3620").Select
Selection.RowHeight = 12
Selection.ColumnWidth = 12
Selection.ClearContents
With Selection.Font
.Name = "Arial"
.Size = 8
.Strikethrough = False
.Superscript = False
.Subscript = False
.OutlineFont = False
.Shadow = False
End With
Range("A1:H5").Select
With Selection
.HorizontalAlignment = xlGeneral
.VerticalAlignment = xlBottom
.WrapText = False
.Orientation = 0
.ShrinkToFit = False
.MergeCells = False
End With
With Selection
.HorizontalAlignment = xlLeft
.VerticalAlignment = xlBottom
.WrapText = False
.Orientation = 0
.IndentLevel = 0
.ShrinkToFit = False
.MergeCells = False
End With
With Selection.Font
.Name = "Arial"
.Size = 11
.Strikethrough = False
.Superscript = False
.Subscript = False
.OutlineFont = False
.Shadow = False
.Underline = xlUnderlineStyleNone
End With
Selection.Font.Bold = True
Selection.Font.ColorIndex = 5
'Imposta i nomi delle colonne
Rows("6:1").Select
Selection.RowHeight = 14
With Selection.Font
.Name = "Arial"
.Size = 11
.Strikethrough = False
.Superscript = False
.Subscript = False
.OutlineFont = False
.Shadow = False
.ColorIndex = xlAutomatic
End With
Selection.Font.Bold = True
Selection.Font.ColorIndex = 5
Range("D2,F3,G5").Select
Range("G5").Activate
With Selection.Font
.Name = "Arial"
.Size = 11
.Strikethrough = False
.Superscript = False
.Subscript = False
.OutlineFont = False
.Shadow = False
.Underline = xlUnderlineStyleNone
.ColorIndex = 5
End With
Selection.Font.Bold = True
With Selection
.HorizontalAlignment = xlCenter
.VerticalAlignment = xlBottom
.WrapText = False
.Orientation = 0
.ShrinkToFit = False
.MergeCells = False
End With
Selection.Font.ColorIndex = 3
Selection.NumberFormat = "0"
Range("A6").Select
ActiveCell.FormulaR1C1 = "Teta"
Range("B6").Select
ActiveCell.FormulaR1C1 = "Alfa"
Range("C6").Select
ActiveCell.FormulaR1C1 = "Ar"
Range("D6").Select
ActiveCell.FormulaR1C1 = "ls"
Range("E6").Select
ActiveCell.FormulaR1C1 = "lr"
Range("F6").Select
ActiveCell.FormulaR1C1 = "N1"
Range("G6").Select
ActiveCell.FormulaR1C1 = "N2"
Range("H6").Select
ActiveCell.FormulaR1C1 = "N3"
Range("I6").Select
ActiveCell.FormulaR1C1 = "Flux_R1"
Range("J6").Select
ActiveCell.FormulaR1C1 = "Flux_R2"
Range("K6").Select
ActiveCell.FormulaR1C1 = "Flux_R3"
Range("L6").Select
ActiveCell.FormulaR1C1 = "Flux_R4"
Range("M6").Select
ActiveCell.FormulaR1C1 = "Flux_R5"
Range("N6").Select
ActiveCell.FormulaR1C1 = "Flux_R6"
Range("O6").Select
ActiveCell.FormulaR1C1 = "Flux_R7"
Range("P6").Select
ActiveCell.FormulaR1C1 = "Flux_R8"
Range("Q6").Select
ActiveCell.FormulaR1C1 = "Flux_R9"
Range("R6").Select
ActiveCell.FormulaR1C1 = "Flux_R10"
Range("S6").Select
ActiveCell.FormulaR1C1 = "Flux_SUM"
Range("T6").Select
ActiveCell.FormulaR1C1 = "F.e.m."
'
Range("A7:W3620").Select
Selection.NumberFormat = "0.00E+00"
Range("A2").Select
'
'Crea una casella di dialogo
'
Incr_vett_alfa = 0.1
Incr_vett_teta = 0.1
N_giri = Application.InputBox("Indicare a quale velocità [rpm] si vuole fare la simulazione.", "N° di GIRI del MOTORE [rpm]")
N_settori = Application.InputBox("Inserire un valore compreso tra [1,10] per specificare il N° di settori in cui dividere il rotore per il calcolo del flusso concatenato.", "N° di settori angolari.")
N_giri_Hertz = 4 * (N_giri / 60) '4 è il numero di coppie polari del motore
'
'
'
Range("A1").Select
ActiveCell.FormulaR1C1 = "Simulazione del motore AFIPM"
Range("E4").Select
ActiveCell.FormulaR1C1 = "Sto calcolando il flusso"
Range("E5").Select
ActiveCell.FormulaR1C1 = "nel settore N°"
Range("A2").Select
ActiveCell.FormulaR1C1 = "in rotazione ad una velocità di"
Range("A3").Select
ActiveCell.FormulaR1C1 = "corrispondente ad una frequenza elettrica di [Hz]"
Range("E2").Select
ActiveCell.FormulaR1C1 = "giri/min"
Range("D2") = N_giri
Range("F3") = N_giri_Hertz
Range("G5").Select
'Inizializza i vettori
Call Calcola_lunghezze(N_settori)
For i = 0 To N_settori - 1
Range("G5") = i + 1 'indica durante il calcolo quale settore sta calcolando
Call Inizializza_Vettori(Lung_tegolo(i), Lung_polo_disp(i), R1(i + 1), R1(i), delta_teta(i), 9 + i)
Next i
'’Calcolo del flusso totale e della f.e.m. a vuoto
For k = 7 To Elem_vett_teta + 7
Range("S" & k) = Range("I" & k) + Range("J" & k) + Range("K" & k) + Range("L" & k) + Range("M" & k)
Range("S" & k) = Range("S" & k) + Range("N" & k) + Range("O" & k) + Range("P" & k) + Range("Q" & k) + Range("R" & k)
Next k
For k = 7 To Elem_vett_teta + 7
Range("T" & k) = ((Range("S" & (k + 1)) - Range("S" & k)) / Incr_vett_teta) * (2 * pi_greco * N_giri_Hertz)
Next k
'
Range("E4").Select
ActiveCell.FormulaR1C1 = " "
Range("E5").Select
ActiveCell.FormulaR1C1 = " "
Range("G5").Select
ActiveCell.FormulaR1C1 = " "
End Sub