Scopo di questa tesi è di illustrare alcuni metodi per la determinazione dei parametri di macchine sincrone a magneti permanenti. Tali metodi saranno applicati al caso particolare di una macchina a flusso assiale a struttura anisotropa. Com’è noto, i metodi convenzionali per la ricerca dei parametri delle macchine sincrone, richiedono la possibilità di regolare l’eccitazione. Ciò non è possibile se la macchina è a magneti permanenti, in quanto i magneti sono dei generatori di flusso costante.
Ai problemi legati alla non regolabilità dell’eccitazione, nel caso del motore studiato in questa tesi, bisogna aggiungere le difficoltà legate alla mancanza del controllo, infatti, non potendo comandare il motore con correnti solo in asse d o solo in asse q, si complica notevolmente il procedimento per la misura delle induttanze Ld ed Lq.
Dopo una breve panoramica, a carattere generale, sulle macchine a flusso assiale ed un rapido confronto con quelle a flusso radiale, si farà una descrizione dettagliata del prototipo di motore a flusso assiale utilizzato (Capitolo 1). Nel secondo capitolo sarà analizzata la prova fatta sul prototipo funzionante come generatore sincrono a vuoto. Scopo di questa prova sarà, oltre a fare una prima stima delle perdite e del flusso concatenato con un avvolgimento di statore, quello di determinare la forma d’onda di tensione a vuoto. Nel terzo capitolo, partendo dalla semplice conoscenza della geometria della macchina e delle caratteristiche dei materiali, sarà descritta una procedura di calcolo per risalire alla forma d’onda di tensione a vuoto, tale forma d’onda sarà poi confrontata con quella misurata.
Nel capitolo quattro sarà descritto un metodo, per la ricerca del modello e la stima dei parametri del motore, basato sull’analisi della risposta in frequenza a rotore bloccato ed alimentato con un piccolo segnale a frequenza variabile, prima in asse d e poi in asse q. Come si vedrà con questa prova non si arriverà a dei risultati validi per la simulazione della macchina in condizione di lavoro reale, essenzialmente per motivi legati alle diverse condizioni di alimentazione del motore durante la prova. Partendo dal modello ottenuto nella prova in frequenza si procederà, nel capitolo cinque, alla determinazione dei parametri mediante l’analisi della risposta al gradino, effettuata a rotore bloccato ed alimentando, come per la prova in frequenza, prima in asse d e poi in asse q. In tale prova il motore sarà chiamato a lavorare con correnti prossime a quelle di reale funzionamento.
In presenza di risultati discordanti, ottenuti con le prove a rotore bloccato, si procederà nel capitolo sei alla descrizione di un’ulteriore prova, volta sostanzialmente a verificare quale delle due prove, effettuate a rotore bloccato, forniva i risultati più attendibili. Tale prova è stata eseguita sulla macchina funzionante da generatore, alimentando due diversi tipi di carico. I risultati ottenuti in questa prova hanno sostanzialmente confermato i risultati ottenuti con la prova di risposta al gradino. Per cercare di capire quali fossero i motivi che hanno portato, nel caso della prova in frequenza, a risultati diversi, sono state effettuate delle prove magnetiche sui materiali utilizzati nella realizzazione del prototipo. In particolare, si è cercato di capire come variava la permeabilità delle ferriti, utilizzate sul rotore della macchina, in presenza di polarizzazione e di piccolo segnale di eccitazione, in pratica, come variava la permeabilità dei materiali nella prova in frequenza. Dai risultati ottenuti dalle prove magnetiche (Capitolo 9), si è riusciti a dare una motivazione ai diversi risultati ottenuti nella prova in frequenza.
Dopo aver trovato il modello della macchina ed aver determinato i valori dei parametri, si è cercato (Capitolo 7) di fare una stima dell’andamento della coppia prodotta dal motore in funzione dell’angolo di carico. Come accennato all’inizio, non avendo un sistema di controllo, la misura di coppia è stata condotta a motore bloccato, variando manualmente i tre valori di corrente rappresentativi di un vettore corrente di modulo costante e rotante su tutti i 360 gradi elettrici, in modo da avere una visione completa dell’andamento della coppia al variare dell’angolo di carico su tutti i 360 gradi elettrici. Con questa prova, utilizzando l’equazione che esprime la coppia in un riferimento bifase sincrono con il rotore, si è risaliti ai parametri della macchina. I risultati ottenuti hanno confermato nuovamente i valori trovati con la prova a carico e con i test di risposta nel tempo. A completamento dello studio fatto per la determinazione dell’andamento della coppia, si è proceduto (Capitolo 8) alla determinazione dell’andamento della coppia di cogging in funzione della posizione angolare del rotore rispetto allo statore.
Nell’ultima parte di questo lavoro, sono riportati due appendici nelle quali si descrivono brevemente: le trasformazioni di variabili e le prove convenzionali utilizzate per la ricerca dei parametri nelle macchine sincrone a campo avvolto. In appendice tre, invece, è riportato il listato dell’algoritmo per la stima della forma d’onda di tensione a vuoto.
Il lavoro per la realizzazione di questa tesi è stato interamente svolto con i mezzi e le apparecchiature messi a disposizione dal Dipartimento di Ingegneria Elettrica Industriale. In particolare la parte sperimentale e la parte relativa alle elaborazioni delle misure è stata svolta presso il Laboratorio di Enertronica del Dipartimento.
Oltre al continuo contatto con i relatori prof. M. Lazzari, prof. F. Profumo ed ing. A. Tenconi, cui volgo i più cordiali ringraziamenti, di particolare aiuto sono stati i consigli ed i chiarimenti dell’ing. A. Cavagnino, soprattutto per quanto riguarda la parte sperimentale.
Per quanto riguarda la stesura della presente, un ringraziamento particolare va a mia moglie, per l’enorme pazienza mostrata durante tutto questo periodo.
Infine, ringrazio i miei genitori, per il loro fondamentale contributo al raggiungimento di questo importante traguardo.
Macchine a Flusso Assiale:
Descrizione del Prototipo AFIPM
1.1 Introduzione
Nella prima parte di questo capitolo, partendo da una panoramica sulle principali differenze esistenti tra i motori a flusso radiale e quelli a flusso assiale, saranno illustrate le varie possibilità realizzative delle macchine a flusso assiale.
La seconda parte sarà dedicata alla descrizione del prototipo studiato in questa tesi. Di seguito per fare riferimento a questo motore verrà spesso utilizzato l’acronimo AFIPM, che è l’abbreviazione della definizione inglese: Axial Flux Interior Permanent Magnet. Tra le principali caratteristiche di questo prototipo vale la pena ricordare che, oltre ad essere una macchina a flusso assiale a struttura anisotropa, questo motore è stato realizzato per applicazioni di deflussaggio, pur essendo un motore a magneti permanenti. Ciò è dovuto alla particolare struttura del rotore che presenta i magneti ricoperti di ferriti per evitare problemi di smagnetizzazione legati alle operazioni di deflussaggio.
1.2 Confronto tra motori a flusso radiale e motori a flusso assiale
In teoria qualsiasi macchina elettrica rotante può essere realizzata, o utilizzando una struttura a flusso radiale oppure utilizzando una struttura a flusso assiale. La figura 1-1 riporta gli schemi principio per la realizzazione di queste due strutture.
Da tali schemi, è facile capire che il nome attribuito alle due strutture è legato alla direzione in cui il flusso magnetico passa dallo statore al rotore. In particolare nelle macchine a flusso radiale il flusso è diretto in direzione radiale, mentre nelle macchine a flusso assiale il flusso è diretto assialmente. Con ciò cambiano, però, anche le superfici utili per la produzione di coppia, in pratica le superfici dove sono disposti i conduttori.
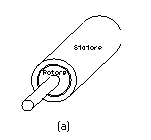
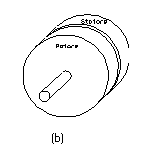
Figura 1-1. Possibili strutture per la realizzazione di macchine elettriche rotanti:
(a) struttura a flusso radiale, (b) struttura a flusso assiale.
Da notare che per le macchine a flusso assiale, è possibile realizzare strutture multistadio, cioè macchine aventi uno o più statori ed uno o più rotori. Ciò porta ad un aumento delle superfici utili per la produzione di coppia e quindi ad una maggiore densità di coppia.
Questo motore, nato in America intorno agli anni ’40, non ha avuto una notevole diffusione, essenzialmente per gli svantaggi economici legati alla produzione in serie dei pacchi lamellari. L’utilizzo è quindi stato confinato a particolari applicazioni in cui era richiesto un ridotto ingombro assiale. Negli ultimi anni grazie alla comparsa di nuovi materiali, ed al progresso in termini di prestazioni e costo degli azionamenti, lo scenario applicativo di queste macchine sta cambiando.
Con riferimento ai motori a magneti permanenti si vogliono ora elencare alcuni vantaggi e svantaggi per le due strutture in esame.
Per i motori a flusso radiale a fronte dei vantaggi rappresentati dal bilanciamento delle forze attrattive tra statore e rotore, alla facilità di asportazione del calore dalla superficie esterna di statore e del basso momento d’inerzia, vi sono gli svantaggi legati alla presenza di un unico traferro disponibile per la generazione della coppia, alla necessità di avere magneti con un lato curvo se affacciati al traferro, alla non regolabilità del traferro in fase di montaggio ed all’aggiunta al traferro dello spessore di collante necessario al fissaggio dei magneti.
Per quanto riguarda i motori a flusso assiale, a fronte dei vantaggi legati alla presenza di più superfici utili alla produzione di coppia (strutture multistadio), alla presenza di magneti con superfici piane anche se direttamente affacciati al traferro, al traferro regolabile durante l’assemblaggio ed alla relativa facilità di realizzazione degli avvolgimenti di statore che è una superficie piana, ci sono gli svantaggi legati alla scarsa utilizzazione degli avvolgimenti (eccessiva lunghezza delle testate esterne), alla difficoltà di posizionamento delle testate al raggio interno (spazio limitato), alla laminazione dei pacchi lamellari in direzione circonferenziale ed alla impossibilità di eliminare il cogging con un skewing lineare.
1.3 Tipologie costruttive per macchine a flusso assiale
Sostanzialmente le tipologie costruttive per le macchine a flusso assiale sono tre. In particolare, sono:
Il prototipo da noi studiato rientra in un caso particolare della struttura AFPM-21, in quanto è una macchina con due statori ed un rotore anisotropo, in cui i magneti sono ricoperti da uno strato di ferriti che hanno la funzione di proteggere i magneti da eventuali rischi di smagnetizzazione. Descriviamo rapidamente le tre strutture prima elencate.
Questa è la più semplice struttura per la realizzazione di motori a flusso assiale. Lo statore ha sostanzialmente la forma di un toro a sezione rettangolare. Le cave sono ricavate su un solo lato dello statore e sono disposte radialmente. Talvolta possono essere disposte in modo leggermente obliquo allo scopo di attenuare la coppia di cogging. Il rotore è costituito da un disco metallico dove, sul lato che si affaccia verso lo statore, sono posizionati i magneti (magnetizzati in direzione assiale).
Questa struttura prevede uno statore e due rotori. Lo statore può essere visto come due statori del tipo AFPM-11, incollati tra loro sui lati privi di cave. I rotori sono perfettamente identici a quello della struttura AFPM-11 e sono disposti sui due lati esterni dello statore. In questa struttura i magneti (magnetizzati assialmente) dei due rotori si possono presentare o con i due poli nord affacciati oppure con un polo nord ed un polo sud affacciati. Nel primo caso è come avere due macchine AFPM-11 attaccate, quindi a parità di diametro del motore si ha una coppia doppia, nel secondo caso il flusso attraversa lo statore assialmente e non circonferenzialmente, quindi l’estensione assiale dello statore non è più dipendente dal flusso che lo attraversa (può causare problemi di saturazione), ciò porta alla realizzazione di macchine più compatte assialmente e quindi a parità di diametro presentano una maggiore densità di coppia.
Questa struttura prevede due statori ed un rotore. Ognuno dei due statori e realizzato in modo identico a quello del motore AFPM-11. Il rotore invece è costituito da un disco di materiale amagnetico sul quale sono ricavati gli alloggiamenti per i magneti, che in questo caso sporgono da entrambi i lati. Il rotore è sistemato tra i due statori. Questa struttura a parità di diametro, avendo due superfici utili alla produzione di coppia, presenta una densità di coppia maggiore rispetto alla struttura AFPM-11.
1.4 Descrizione del motore AFIPM
La struttura AFIPM utilizzata nel prototipo in studio, come accennato all’inizio del paragrafo precedente, è sostanzialmente la stessa adottata nei motori AFPM-21. L’unica differenza consiste nella ricopertura dei magneti, cerchiamo di capire a cosa serve. Una caratteristica importante richiesta al prototipo è la possibilità di essere comandato al di sopra della velocità base e fino ad una velocità massima in modo tale da fornire una potenza costante. In questo modo è possibile ridurre la potenza apparente nominale dell’inverter di alimentazione. Ciò richiede che il motore sia deflussabile, cioè che sia possibile diminuire opportunamente il flusso concatenato con gli avvolgimenti di statore. Come è facilmente intuibile, quest’operazione è assai difficile con un motore tradizionale a magneti permanenti. Essendo i magneti dei generatori ideali di flusso, per definizione non è possibile variare tale flusso agendo sulle correnti di statore, a meno che non si accetti di smagnetizzare il magnete. Viceversa, ricoprendo opportunamente i magneti con del materiale ferromagnetico, si creano dei percorsi alternativi, per il flusso prodotto dai magneti, quando si è in presenza di correnti smagnetizzanti statoriche, ciò permette una buona deflussabilità della macchina.
La figura 1-2 mostra la struttura del prototipo AFIPM in studio.
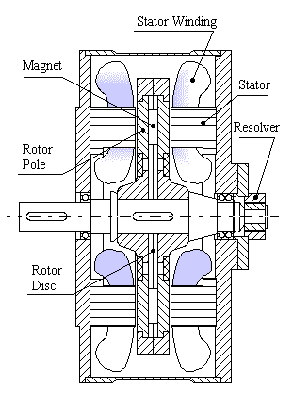
Figura 1-2. Struttura del prototipo AFIPM in studio.
In questo prototipo, gli statori sono realizzati con un lamierino avvolto a nastro e le cave sono realizzate in direzione radiale su una delle due facce di ciascuno statore. Tali statori sono stati collegati agli scudi esterni in modo che le cave risultino tra loro affacciate. Gli avvolgimenti di statore sono stati realizzati in modo che il rotore non debba garantire la richiusura del flusso. Così facendo non è necessario il giogo rotorico e quindi la lunghezza assiale del motore è ulteriormente ridotta. La figura 1-3 mostra una sezione rettificata al raggio medio del motore AFIPM.
Vediamo ora com’è stato realizzato il rotore della macchina. Sul disco di acciaio amagnetico che costituisce la parte portante del rotore, sono stati ricavati degli alloggiamenti per i magneti permanenti. Dopo aver sistemato i magneti negli alloggiamenti, il disco è stato ricoperto con due anelli di ferriti dolci per applicazioni in bassa frequenza. Ovviamente, per evitare di cortocircuitare il flusso prodotto dai magneti si sono realizzate in ogni passo polare, due tagli negli anelli di ferrite.
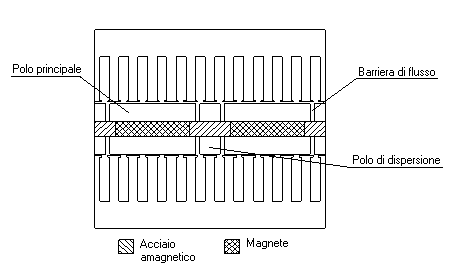
Figura 1-3. Sezione rettificata del prototipo AFIPM.
Questi tagli, chiamati barriere di flusso, dividono i poli principali da quelli di dispersione.
La funzione dei poli principali è, oltre a proteggere i magneti dal pericolo di smagnetizzazione, quella di creare un’adatta distribuzione di induzione al traferro. Si noti, infatti, che quando viene inviata una corrente smagnetizzante in asse d, il flusso prodotto dai magneti viene deviato attraverso i poli di dispersione. I poli di dispersione hanno il compito di creare una salienza apprezzabile nella macchina. Poiché, i magneti sono ricoperti dalle ferriti, il traferro è piccolo, quindi le induttanze della macchina sono elevate. I valori di tali induttanze dipendono dalla geometria della macchina, di conseguenza la posizione delle barriere di flusso influenza tali parametri. Ne consegue che volendo ottenere determinati valori dei parametri per garantire la coppia richiesta nell’intervallo desiderato, è necessario posizionare opportunamente le barriere di flusso.
Tenendo conto che la macchina è a magneti permanenti e che sugli statori sono presenti delle cave, ci sarà sicuramente una coppia parassita di cogging. Conoscendo questo inconveniente già in fase di progetto, si è cercato di ridurre l’effetto di questa coppia agendo sulla direzione delle barriere di flusso. In particolare, tali barriere sono state inclinate di circa un passo di dentatura, con la speranza di ridurre la coppia di cogging. La figura 1-4 mostra lo schema del rotore del prototipo AFIPM e riporta le equazioni dei tagli (rette) riferite ai riferimenti rappresentati nella figura stessa. La figura 1-5 riporta un particolare del rotore e le coordinate, riferite al riferimento X-Y, dei vari elementi che lo costituiscono.
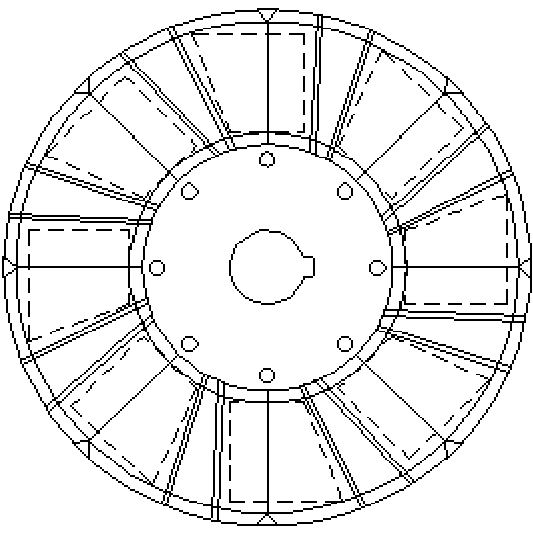
Figura1-4. Schema del rotore del prototipo AFIPM. Con le linee tratteggiate si sono rappresentati i magneti posizionati sotto gli anelli di ferrite.
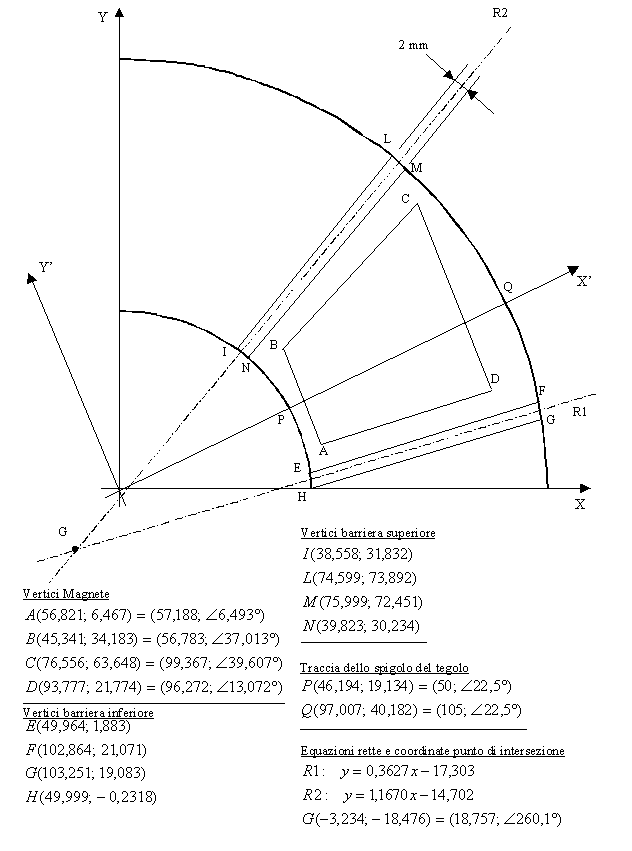
Figura 1-5. Particolare costruttivo del rotore e coordinate dei vari elementi rispetto al sistema di riferimento X-Y.
Funzionamento a Vuoto
2.1 Introduzione
In questa prova il prototipo AFIPM è fatto funzionare come generatore sincrono a magneti permanenti, trascinato in rotazione da un motore a corrente continua. Gli avvolgimenti corrispondenti dei due statori della macchina, sono stati collegati in serie in modo da ottenere la massima tensione in uscita.
Lo scopo di questa prova, oltre a verificare la forma d’onda di tensione generata dalla macchina, è quello di fare una prima stima del flusso concatenato con gli avvolgimenti di statore. È inoltre possibile, in questa prova, fare una valutazione delle perdite nel ferro e delle perdite dovute agli attriti, misurando la potenza meccanica nelle varie prove a vuoto.
2.2 Rilevazione della f.e.m. a vuoto
Collegati in serie gli avvolgimenti corrispondenti dei due statori, si è portato in rotazione il prototipo con un motore a corrente continua. Tra l’albero della macchina a collettore e quello del prototipo è stato interposto un sensore di coppia, in modo da poter verificare quale coppia veniva trasmessa al motore in prova alle varie velocità di funzionamento. Le tre fasi del motore sono state collegate ai tre canali d’ingresso di un oscilloscopio digitale. Al variare della velocità della macchina si sono rilevate le varie forme d’onda di f.e.m. a vuoto. La figura 2-1 mostra un esempio di f.e.m. a vuoto rilevate sulle tre fasi del motore e le corrispondenti fondamentali, relative ad una velocità di rotazione di 450 rpm.
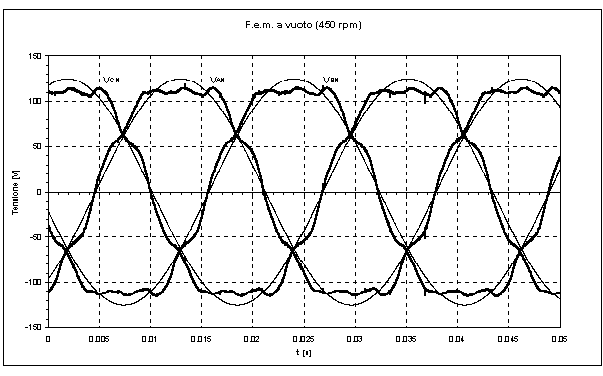
Figura 2-1. Forme d'onda rilevate sulle tre fasi del motore AFIPM alla velocità di 450 rpm.
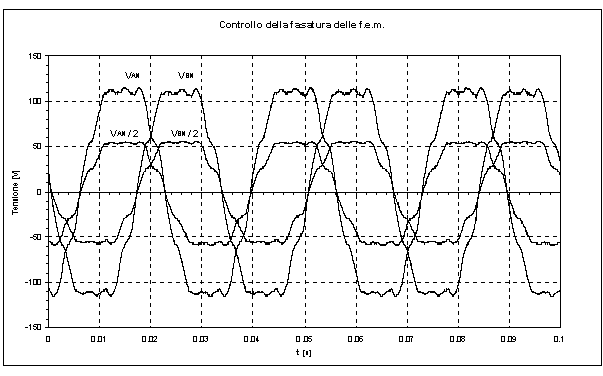
Figura 2-2. F.e.m. a vuoto rilevate ai capi degli avvolgimenti dei due statori collegati in serie, e f.e.m. a vuoto rilevate ai capi degli avvolgimenti dei singoli statori.
Determinate le forme d’onda delle f.e.m. sulle tre fasi, si è proceduto a verificare se tali forme d’onda erano date dalla semplice somma algebrica delle corrispondenti tensioni sugli avvolgimenti dei singoli statori, oppure erano dovute ad una somma vettoriale. Per fare ciò si sono rilevate nello stesso istante le forme d’onda delle f.e.m. sia come somma delle tensioni sugli avvolgimenti corrispondenti dei singoli statori che come tensione indotta sull’avvolgimento del singolo statore. La figura 2-2 riporta un esempio di tale misura. Da tale figura si può notare che le tensioni risultano perfettamente in fase, quindi la tensione totale corrisponde alla somma algebrica delle tensioni sugli avvolgimenti corrispondenti dei singoli statori.
Dall’analisi delle forme d’onda di tensione a vuoto, si può verificare una certa asimmetria tra i fronti di salita della tensione e quelli di discesa. Tale asimmetria è funzione del verso di rotazione, in particolare invertendo il verso di rotazione la forma d’onda di tensione che si ottiene, risulta ribaltata a specchio (lungo le ordinate) rispetto a quella di figura 2-1. Ciò e da attribuirsi probabilmente alla forma delle barriere di flusso, che non avendo il centro di taglio coincidente con il centro di rotazione (si pensi a com’è fatto il rotore della macchina), influiscono diversamente sulla forma d’onda di tensione in funzione del verso di rotazione.
2.3 Determinazione delle perdite
Facendo funzionare la macchina come generatore a vuoto, e nota la coppia fornita dal motore a corrente continua, è immediato risalire alle perdite nel ferro e per attrito del prototipo AFIPM.
Infatti, nell’ipotesi di trascurare la piccolissima potenza assorbita dallo strumento di misura, si può affermare che tutta la potenza meccanica fornita in ingresso al motore si trasforma in perdite. In formule:
![]() (2-1)
(2-1)
La figura 2-3 mostra l’andamento di tali perdite in funzione della velocità angolare.
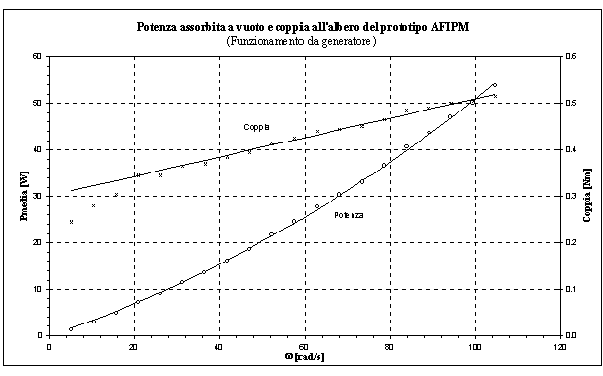
Figura 2-3. La curva relativa alla potenza assorbita coincide, nelle ipotesi fatte, con le perdite nel ferro e per attrito del prototipo AFIPM.
2.4 Flusso concatenato con gli avvolgimenti di statore
Note le forme d’onda di tensione a vuoto, si può risalire facilmente per via numerica alla fondamentale. Riportando su un grafico in funzione della velocità angolare i valori efficaci di tali fondamentali, è immediato risalire all’equazione che lega il valore efficace di f.e.m. al numero di giri, cioè:
![]() (2-2)
(2-2)
Ricordando che la ![]() si può esprimere anche come:
si può esprimere anche come:
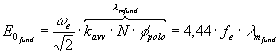 (2-3)
(2-3)
e la relazione che lega la frequenza elettrica al numero di giri espresso in rpm è:
![]() (2-4)
(2-4)
dove p è il numero di coppie polari della macchina, posso determinare ![]() uguagliando la (2-2) con la (2-3), cioè:
uguagliando la (2-2) con la (2-3), cioè:
![]() (2-5)
(2-5)
In figura 2-4 è riportato l’andamento della ![]() in funzione del numero di giri.
in funzione del numero di giri.
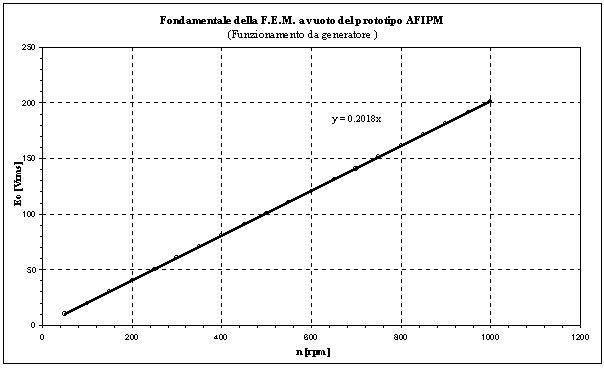
Figura 2-4. Valore efficace della fondamentale della F.E.M. a vuoto in funzione del numero di giri, e retta interpolante con relativa equazione.
Nel nostro caso KE = 0,2018 e p = 4, quindi sostituendo nella (2-5), trovo per ![]() il valore di 0,68 Wb.
il valore di 0,68 Wb.
Stima della Forma d’Onda della F.e.m. a Vuoto
3.1 Introduzione
In questo capitolo si descriverà il procedimento (d’ora in poi Algoritmo) seguito per determinare la forma d’onda di tensione prodotta dal motore AFIPM nel funzionamento a vuoto, partendo dalla sola conoscenza della geometria del motore. Questo può essere un passo importante in fase di progettazione, in quanto può dare una stima della forma d’onda della tensione prodotta dal motore prima ancora della realizzazione del prototipo.
Non essendo un procedimento utilizzato frequentemente, si è reso necessario un confronto dei risultati ottenuti con questo metodo con i risultati ottenuti sperimentalmente (vedi capitolo precedente). Nei prossimi paragrafi verranno descritte le varie funzioni elementari utilizzate nell’Algoritmo. Si farà infine un confronto con la forma d’onda di tensione a vuoto ottenuta sperimentalmente.
3.2 Funzione distribuzione di conduttori N(
a )La macchina in esame è una macchina a 4 coppie polari con due statori ed un rotore. Su ogni statore sono ricavate 48 cave per l’alloggiamento dei conduttori, questo significa che ad ogni avvolgimento di uno statore, sono riservate 2 cave per polo per fase. La figura 3-1 mostra lo schema di principio utilizzato per descrivere la distribuzione di conduttori in funzione dell’angolo di traferro a . Tale distribuzione di conduttori è stata ricavata nell’ipotesi di avvolgimenti concentrati, si è quindi considerata in ogni cava una singola spira equivalente.
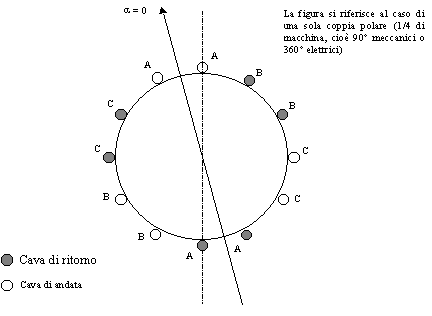
Figura 3-1. Macchina semplificata ad una sola coppia polare utilizzata per descrivere la distribuzione di conduttori in funzione dell’angolo di traferro
a .
Partendo dalla figura 3-1, nota la geometria dello statore, è immediato determinare la distribuzione di conduttori con le ipotesi fatte. La figura 3-2 mostra la distribuzione NA(a ), determinata con l’utilizzo della routine, Visual Basic, utilizzata nell’Algoritmo.
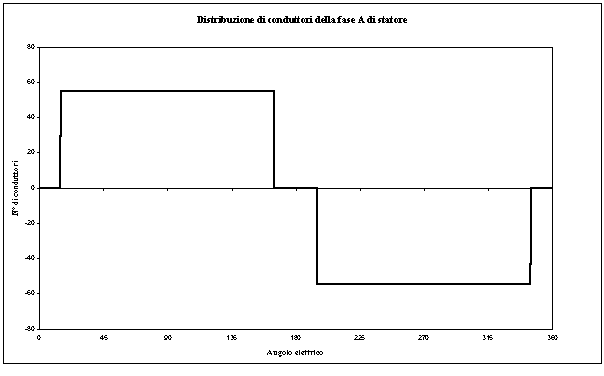
Figura 3-2. La figura mostra la funzione distribuzione di conduttori, NA (
a ), calcolata con il l’algoritmo di simulazione.
Le distribuzioni NB(a ) ed NC(a ) hanno lo stesso andamento ma risultano sfasate rispetto ad NA(a ), rispettivamente di 120 e 240 gradi elettrici.
3.3 Funzione lunghezza di traferro vista da rotore
Per determinare la lunghezza di traferro vista da rotore è necessario porsi come un osservatore solidale con il rotore. Da tale posizione si può osservare che la lunghezza di traferro è una funzione periodica, con periodo pari a 30 gradi elettrici.
La figura 3-3 mostra l’andamento in funzione dell’angolo a della lunghezza di traferro meccanica, riferita ad un raggio Rx.
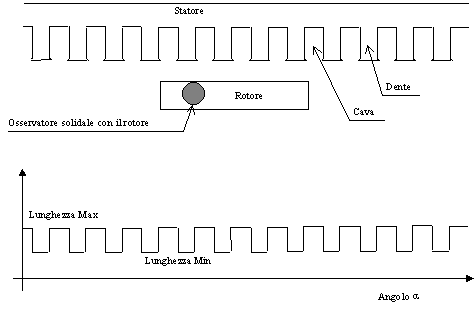
Figura 3-3. La figura mostra l’andamento in funzione dell’angolo
a della lunghezza meccanica di traferro, calcolata su una circonferenza di raggio Rx, relativa ad un quarto di macchina (360° elettrici).è importante osservare che essendo la macchina a flusso assiale, cambiando il raggio Rx a cui si riferisce la figura 3-3 cambiano anche le proporzioni, intese come estensione angolare, tra denti e cave.
Dal punto di vista magnetico quello che interessa è una lunghezza diversa da quella meccanica, ed in particolare è la lunghezza equivalente di traferro che vedono le linee di campo magnetico. Per fare ciò, si sono formulate le seguenti ipotesi:
Con le ipotesi fatte, definita una coordinata lineare x di traferro con origine nella mezzeria della cava, è possibile ricavare la componente perpendicolare alla superficie di rotore del campo magnetico all’interno della cava con le seguenti relazioni:
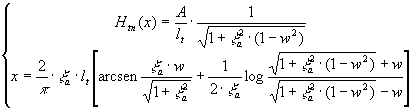 (3-1)
(3-1)
dove ![]() mentre w è una variabile che assume tutti i valori compresi tra 0 ed 1 quando x varia tra 0 ed infinito. Definito
mentre w è una variabile che assume tutti i valori compresi tra 0 ed 1 quando x varia tra 0 ed infinito. Definito ![]() , è possibile risalire alla lunghezza equivalente di traferro dal punto di vista magnetico attraverso la seguente relazione:
, è possibile risalire alla lunghezza equivalente di traferro dal punto di vista magnetico attraverso la seguente relazione:
![]() (3-2)
(3-2)
La figura 3-4 mostra l’andamento della lunghezza equivalente di traferro, calcolata secondo questo procedimento da una routine dell’Algoritmo. Si ricorda, inoltre, che tale lunghezza è funzione esclusivamente dell’angolo di traferro a .
3.4 Funzione lunghezza equivalente di traferro vista da statore
Per determinare la lunghezza equivalente di traferro vista da statore, è necessario porsi come un osservatore solidale con lo statore. Da tale posizione si può osservare che la lunghezza equivalente di traferro è una funzione periodica, con periodo pari a 180 gradi elettrici.
La figura 3-5 mostra l’andamento in funzione dell’angolo a della lunghezza di traferro meccanica vista da statore.
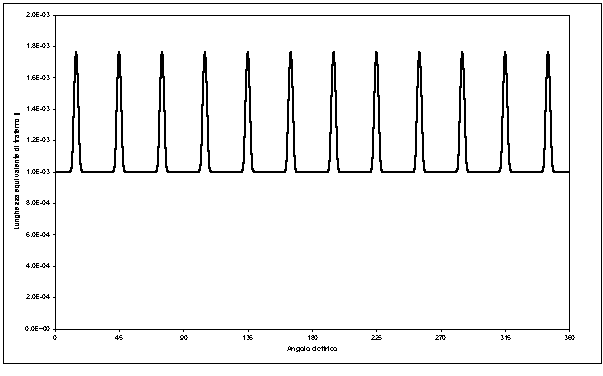
Figura 3-4. Andamento della lunghezza equivalente magnetica di traferro vista da un osservatore solidale con il rotore, calcolata con l’algoritmo di simulazione.
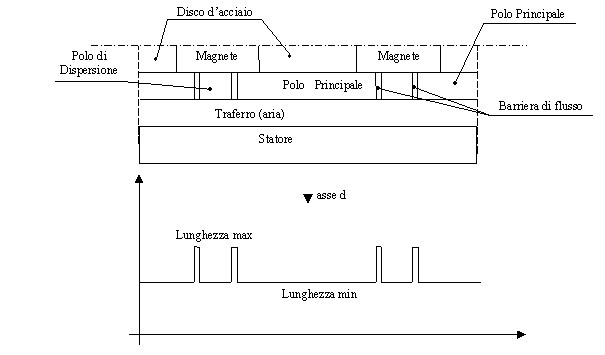
Figura 3-5. La figura mostra l’andamento in funzione dell’angolo
a della lunghezza meccanica di traferro vista da statore, calcolata su una circonferenza di raggio Rx, relativa ad un quarto di macchina (360° elettrici).
Anche per questa lunghezza quello che interessa è la lunghezza equivalente magnetica, che si calcola con lo stesso procedimento visto al paragrafo precedente.
In figura 3-6 si riporta l’andamento in funzione dell’angolo a della lunghezza equivalente magnetica, calcolata con una routine dell’Algoritmo.
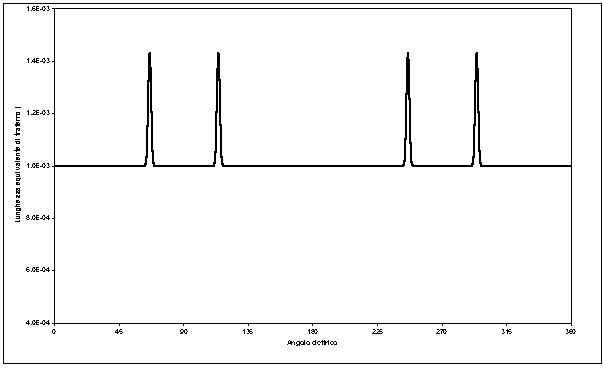
Figura 3-6. Andamento della lunghezza equivalente magnetica di traferro vista da un osservatore solidale con lo statore, calcolata con l’algoritmo di simulazione.
In questo caso, tale lunghezza equivalente non è funzione solo dell’angolo a ma dipende dalla differenza a - J , dove J è l’angolo tra la coordinata a = 0 di statore e l’asse d di rotore.
Nell’Algoritmo non si utilizza singolarmente l’una o l’altra lunghezza, ma una lunghezza magnetica equivalente che risulta dalla somma delle due lunghezze prima citate, depurate del valore della lunghezza al traferro sotto i denti, cioè:
![]() (3-3)
(3-3)
3.5 Funzione f.m.m. di rotore al traferro
Per individuare la forma d’onda di f.m.m. al traferro, consideriamo come al solito solo un quarto di macchina, nella restante parte della macchina le cose si ripetono periodicamente allo stesso modo.
Si facciano le seguenti ipotesi:
Con queste ipotesi è immediato determinare l’andamento della f.m.m. al traferro. La figura 3-7 mostra tale andamento, riportato in funzione della geometria del motore.
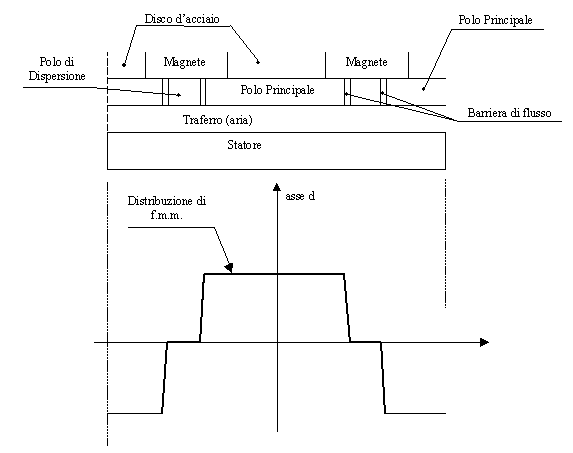
Figura 3-7. Distribuzione di f.m.m. al traferro.
Da notare che anche tale forma d’onda dipende dall’angolo a -J .
La figura 3-8 mostra l’andamento della f.m.m. al traferro, determinata utilizzando la funzione Visual Basic utilizzata nell’Algoritmo. È importante osservare che tale funzione non è l’unica possibile ipotizzabile, inoltre di tale funzione non si è ancora calcolato il valore numerico che ne rappresenta l’ampiezza.
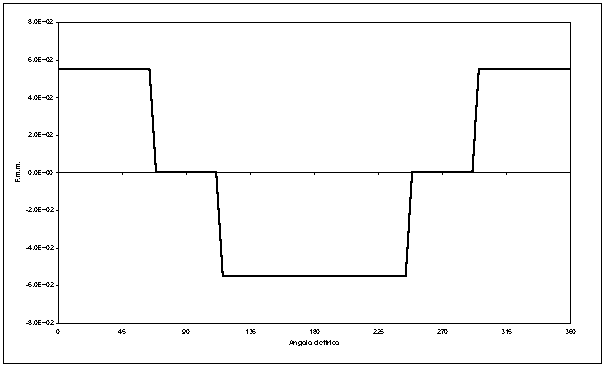
Figura 3-8. Andamento della distribuzione di f.m.m. calcolata con l’utilizzo dell’algoritmo ipotizzando un ampiezza
pari a 551 Asp, risultato del procedimento illustrato nel paragrafo 3-6.
3.6 Determinazione dell’ampiezza della f.m.m. al traferro
Per determinare l’ampiezza di f.m.m. al traferro è necessario conoscere il valore di campo magnetico al traferro, e quindi d’induzione. Partendo dai dati ottenuti dalla prova a vuoto e ricordando che:
![]() (3-3)
(3-3)
è possibile dire, ricordando l’espressione analitica della ![]() , che:
, che:
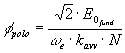 (3-4)
(3-4)
dove ![]() e
e ![]() . Sostituendo i valori numerici nella (3-4) trovo:
. Sostituendo i valori numerici nella (3-4) trovo:
![]() (3-5)
(3-5)
Ma ![]() può essere espresso analiticamente, nell’ipotesi semplificativa di distribuzione ad onda quadra, come:
può essere espresso analiticamente, nell’ipotesi semplificativa di distribuzione ad onda quadra, come:
![]() (3-6)
(3-6)
dove ![]() è l’estensione del passo polare, e nel nostro caso al raggio medio vale:
è l’estensione del passo polare, e nel nostro caso al raggio medio vale:
![]() (3-7)
(3-7)
Esplicitando dalla (3-6) la ![]() e sostituendo i valori reali (
e sostituendo i valori reali (![]() e
e ![]() ) trovo:
) trovo:
![]() (3-8)
(3-8)
La (3-8) esprime il valore d’induzione magnetica al traferro determinata partendo dai dati sperimentali. Quello che interessa, però, è un metodo che porti ad una valutazione realistica del campo al traferro partendo dalla sola conoscenza della geometria della macchina e delle caratteristiche dei materiali. Si ricorda, infatti, che lo scopo dell’Algoritmo è la ricerca della forma d’onda di f.e.m. a vuoto in fase di progetto, in pratica prima della realizzazione fisica del prototipo.
Per fare ciò si è fatta l’ipotesi che il ferro abbia permeabilità infinita, e l’induzione al traferro abbia l’andamento riportato in figura 3-9.
Trascurando le dispersioni laterali del magnete il circuito equivalente si può ricavare facilmente dallo schema di figura 3-9. Per maggiore chiarezza si riporta in figura 3-10 il circuito equivalente considerato.
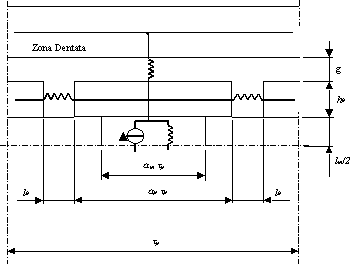
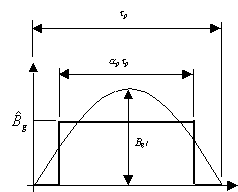
Figura 3-9. Schema di riferimento per il calcolo dell’induzione al traferro. La figura si riferisce ad un solo polo della macchina e metà lunghezza assiale.
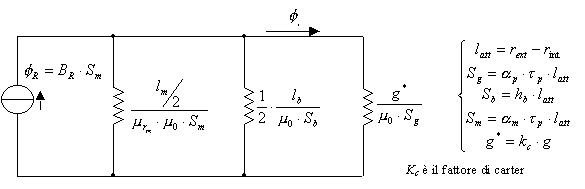
Figura 3-10. Circuito elettrico equivalente, per la determinazione dell’induzione al traferro.
Definite le quantità 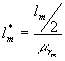 e
e ![]() con alcuni passaggi matematici il circuito di figura 3-10 diventa quello riportato in figura 3-11. Dall’analisi di tale circuito si perviene alla relazione:
con alcuni passaggi matematici il circuito di figura 3-10 diventa quello riportato in figura 3-11. Dall’analisi di tale circuito si perviene alla relazione:
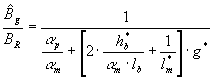 (3-9)
(3-9)
sostituendo in tale relazione i valori relativi alla geometria ed ai materiali utilizzati nel prototipo AFIPM (vedi tabella 3-1) si ottiene 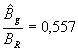 da cui
da cui ![]() .
.
Si vede subito che con tale procedimento si sovrastima il valore d’induzione al traferro, bisognerà quindi perfezionare tale metodo tenendo conto dei flussi dispersi.
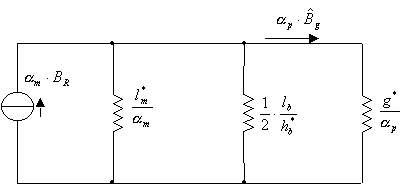
Figura 3-11. Circuito equivalente elettrico semplificato.
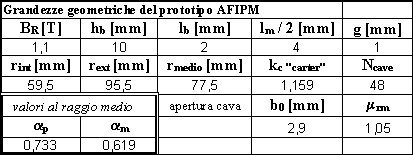
Tabella 3-1. Valori numerici delle grandezze geometriche del prototipo AFIPM.
In particolare è possibile considerare i flussi dispersi dovuti all’area tratteggiata di figura 3-12. Tali flussi dispersi si traducono nel circuito elettrico equivalente di figura 3-11 in un ulteriore ramo resistivo in parallelo, il cui valore è:
![]() (3-10)
(3-10)
Risolvendo tale circuito, come è già stato fatto per il circuito di figura 3-11, si arriva ad una espressione simile alla (3-9) e sostituendo in tale equazione i valori tipici della macchina si ottiene un valore di flusso leggermente più vicino a quello misurato (![]() ).
).
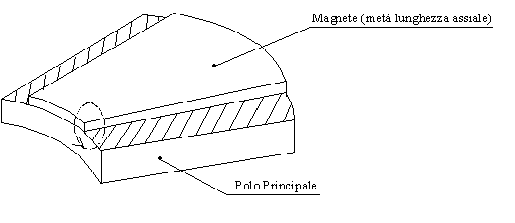
Figura 3-12. La figura mostra una parte del rotore alla quale si può attribuire parte del flusso disperso.
La differenza tra valore calcolato e il valore misurato, può dipendere dall’aver sviluppato tutti questi calcoli facendo riferimento al raggio medio. Si è allora proceduto, con l’ausilio di un foglio elettronico, alla suddivisione del motore in mille settori circolari ed in ognuno dei settori si sono ripetuti i calcoli prima esposti. Dal valore di ![]() trovato, utilizzando la relazione:
trovato, utilizzando la relazione: ![]() , si è ottenuto un valore di f.m.m. pari a 551 Aasp.
, si è ottenuto un valore di f.m.m. pari a 551 Aasp.
3.7 Calcolo del flusso concatenato e della f.e.m. a vuoto
Dopo aver descritto le varie funzioni utilizzate nell’Algoritmo, si descrive il procedimento seguito per la ricerca del flusso concatenato con un avvolgimento di statore. Partiamo dalla relazione che esprime il flusso concatenato con un avvolgimento A di statore in funzione della posizione assunta dal rotore:
![]()
![]() (3-11)
(3-11)
dove:
è la superficie infinitesima attraverso la quale viene valutato il flusso.
Per il calcolo numerico della forma d’onda del flusso concatenato si è proceduto calcolando per ogni posizione J del rotore la relazione (3-11). In particolare si è fatto ruotare l’angolo J di 0,1 gradi elettrici fino ad esplorare tutti i 360 gradi elettrici, e per ogni posizione occupata dal rotore si è valutata numericamente la (3-11). Per la valutazione numerica della (3-11) si è proceduto, per ognuna delle 3600 diverse posizioni assunte dal rotore, al calcolo dell’integrando della (3-11) come sommatoria dei 3600 flussi infinitesimi legati ad altrettanti settori angolari di ampiezza pari a 0,1 gradi elettrici. In formule, tale ragionamento può essere espresso come:
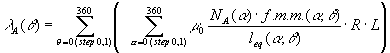 (3-12)
(3-12)
Per tenere conto, nel calcolo del flusso concatenato, dell’effetto delle barriere di flusso sulla forma d’onda di f.e.m. indotta negli avvolgimenti, si è proceduto alla suddivisione della parte attiva della macchina in dieci settori circolari e in ognuno dei dieci settori si è valutata la (3-12). Il flusso totale concatenato con l’avvolgimento di statore è, quindi, dato dalla somma dei vari flussi calcolati nei dieci settori. La figura 3-13 mostra, sia l’andamento dei flussi nei vari settori circolari, che il flusso totale dato dalla somma dei dieci flussi. Dall’analisi di tale figura si vede subito che i flussi nei dieci settori non sono in fase tra loro, ciò è dovuto alla presenza delle barriere di flusso che spostano, di fatto, il baricentro della parte attiva considerata in funzione del raggio e quindi del settore angolare considerato.
Nota la forma d’onda del flusso concatenato con l’avvolgimento, è immediato risalire alla forma d’onda di f.e.m. indotta, attraverso la relazione:
![]() (3-13)
(3-13)
La figura 3-14 mostra l’andamento di tale forma d’onda.
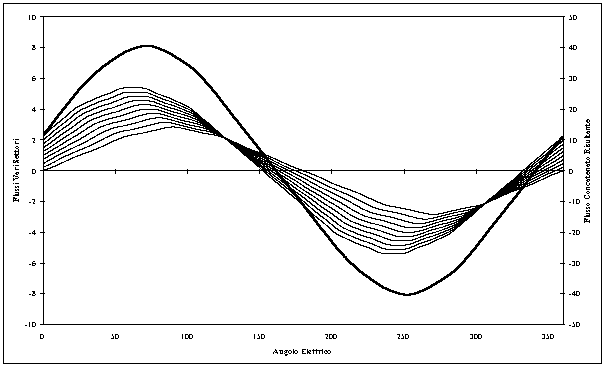
Figura 3-13. Andamento dei flussi concatenati relativi ai vari settori e flusso risultante (in neretto).
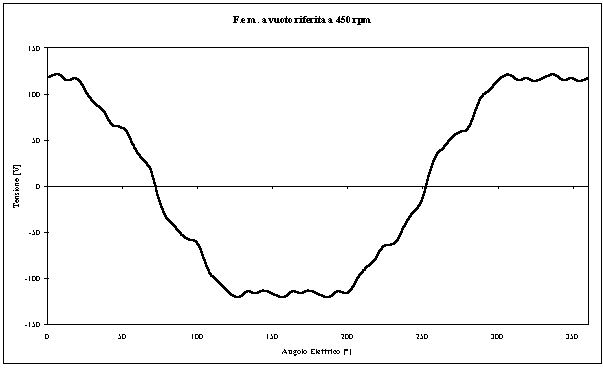
Figura 3-14. Andamento della f.e.m. indotta in un avvolgimento di statore a vuoto.
3.8 Confronto tra la forma d’onda misurata e quella calcolata
Dopo aver illustrato il procedimento seguito dall’Algoritmo per il calcolo della forma d’onda di tensione, si procede ad un confronto tra la forma d’onda di tensione misurata e quella calcolata. La figura 3-15 mostra tali forme d’onda a confronto.
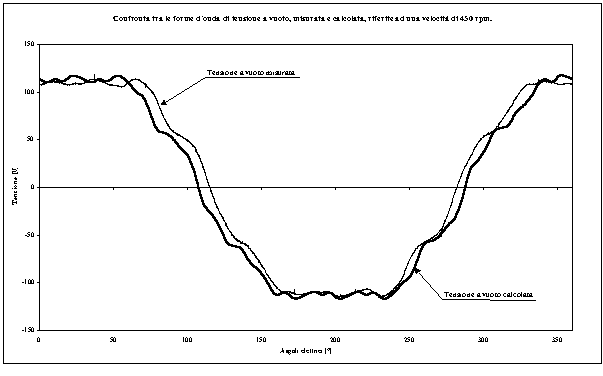
Figura 3-15. Confronto tra la forma d’onda di tensione a vuoto misurata e calcolata.
Dall’analisi della figura 3-15, trascurando la leggera differenza di frequenza tra le due forme d’onda, da attribuirsi alla scarsa affidabilità della regolazione manuale della velocità durante la misura, è possibile notare una maggiore distorsione nella forma d’onda calcolata. Tale effetto era prevedibile, infatti, nell’Algoritmo sono state fatte delle ipotesi semplificative, tra le quali quella di non considerare l’influenza del ferro. Ciò ha portato a non considerare gli effetti dovuti alla presenza di correnti parassite indotte nel ferro di statore, che nella realtà contribuiscono alla riduzione della distorsione della forma d’onda agendo come dei circuiti smorzatori. È interessante osservare, inoltre, come l’Algoritmo riesca a simulare bene l’effetto dovuto alla presenza delle barriere di flusso che generano una piccola punta nella parte terminale della zona di massimo/minimo nel verso di rotazione.
Alla luce di tali risultati è possibile affermare che il procedimento utilizzato per simulare la forma d’onda di tensione a vuoto, ha portato a risultati soddisfacenti.
Prove di Risposta in Frequenza
4.1 Introduzione
La prima fase, quella più importante, per lo studio del comportamento dinamico di una macchina è la ricerca del modello che meglio approssima il comportamento reale. Essendo la macchina ancora in fase di studio, è stato necessario procedere con delle prove direttamente sul prototipo. Per fare ciò si sono effettuate delle prove in frequenza a rotore bloccato. Dall’analisi del comportamento del prototipo AFIPM in queste prove, si è risalito ad un primo modello della macchina.
Il passo successivo all’individuazione del modello, è quello della determinazione dei parametri. Cioè, noto il modello è stato necessario determinare i valori da assegnare ai parametri per ottenere la migliore approssimazione del comportamento reale della macchina, in ogni condizione di funzionamento.
In questo capitolo si descriverà il procedimento seguito per eseguire la prova, si cercherà di analizzare i risultati ottenuti e si procederà in modo ragionato alla ricerca del modello, infine si farà una prima stima dei parametri della macchina AFIPM.
4.2 Posizionamento del rotore in asse d
Il primo passo, nell’eseguire questa prova, consiste nel corretto posizionamento del motore in asse d. Questa fase è molto importante, in quanto un piccolo errore nel posizionamento può avere come conseguenza una significativa variazione dell’impedenza della macchina. La figura 4-1 mostra lo schema elettrico di principio utilizzato per eseguire il posizionamento.
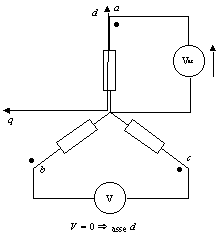
Figura 4-1. Schema elettrico di principio utilizzato per il posizionamento del rotore in asse d.
Collegate le tre fasi del motore a stella, è stata alimentata la fase a con una tensione sinusoidale (![]() a
a ![]() ), ottenuta da una coppia generatore di funzioni, amplificatore lineare di potenza. Per la ricerca dell’asse d, è stato necessario ruotare il rotore in modo da ottenere tra le fasi b e c una tensione nulla.
), ottenuta da una coppia generatore di funzioni, amplificatore lineare di potenza. Per la ricerca dell’asse d, è stato necessario ruotare il rotore in modo da ottenere tra le fasi b e c una tensione nulla.
Il problema principale nel fare ciò è stato la presenza del cogging, che rendeva difficile variare finemente la posizione angolare del rotore. Raggiunto tra le fasi b e c un valore di qualche millivolt si è proceduto a bloccare il rotore. Tenuto conto delle difficoltà di posizionamento e volendo ottenere risultati comparabili tra le misure in asse d ed in asse q, non è stato ritenuto opportuno variare fisicamente la posizione del rotore per alimentare il prototipo in asse q ma si è proceduto cambiando opportunamente i collegamenti delle fasi del motore. La figura 4-2 mostra gli schemi utilizzati per alimentare il motore in asse d ed in asse q mantenendo il rotore bloccato in asse d.
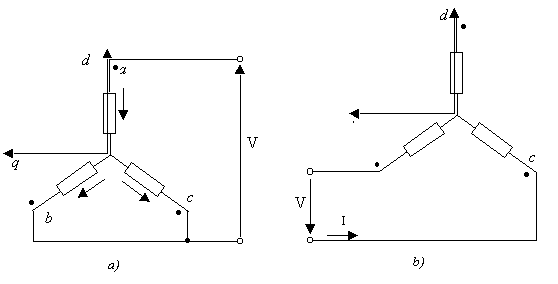
Figura 4-2. a) Schema utilizzato per alimentare il motore in asse d, con rotore bloccato in asse d; b) Schema utilizzato per alimentare il motore in asse q, con rotore bloccato in asse d.
Alimentando il prototipo in regime sinusoidale a frequenza variabile, nell’intervallo da 10 mHz fino ad 1 kHz prima in asse d e poi in asse q, si è cercato di determinare l’impedenza operazionale del motore espressa per i due assi, tenendo conto dei collegamenti, dalle seguenti relazioni:
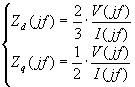 (4-1)
(4-1)
Nel campo di frequenze da 1 kHz fino a 10 Hz tale impedenza è stata misurata utilizzando un impedenzimetro vettoriale, mentre nel restante intervallo di frequenze, ![]() (basse frequenze), si è proceduto manualmente. Lo schema di principio utilizzato per le misure a bassa frequenza è riportato in figura 4-3.
(basse frequenze), si è proceduto manualmente. Lo schema di principio utilizzato per le misure a bassa frequenza è riportato in figura 4-3.
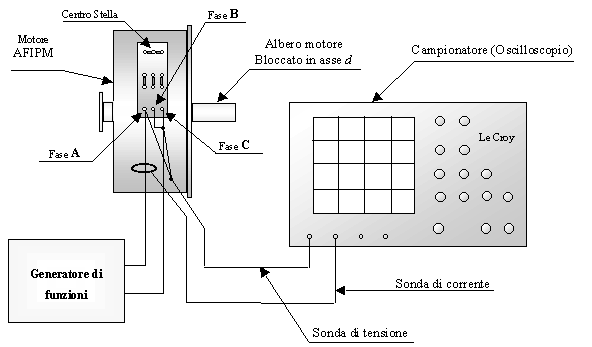
Figura 4-3. Circuito utilizzato per rilevare l’impedenza operazionale in asse d del prototipo AFIPM, per i valori di frequenza compresi tra 10 mHz e 10 Hz.
Il generatore di funzioni utilizzato era in grado di generare forme d’onda sinusoidali poco distorte fino a circa 10 mHz, con correnti di circa 100 mA (circa il 2 % della corrente nominale del motore). Come campionatore di segnale si è utilizzato un oscilloscopio digitale ad elevata frequenza di campionamento (Le Croy).
Partendo da 10 Hz e diminuendo di volta in volta la frequenza di alimentazione di 10 mHz fino ad arrivare al valore minimo di frequenza, si sono rilevate le forme d’onda di tensione e di corrente ai capi del motore. In figura 4-4 è stato riportato un esempio di forme d’onda campionate.

Figura 4-4. Andamento grafico di tensione e corrente ai capi del motore e relative fondamentali. Tale figura si riferisce ad una misura fatta in asse d alla frequenza di 90 mHz.
Analizzando la figura 4-4 si può notare la notevole l’influenza dei disturbi ad alta frequenza sul segnale misurato. Poiché in questa misura interessa determinare l’impedenza operazionale in modulo e fase, e ricordando che per ogni valore di frequenza tali grandezze sono definite come:
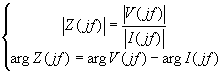 (4-2)
(4-2)
si capisce che la presenza dei disturbi può influire negativamente sulla stima delle ampiezze e delle fasi delle grandezze misurate. È quindi necessario tenere conto di ciò nell’elaborazione dei dati. Questo è stato fatto per via numerica utilizzando il metodo dei minimi quadrati e ricercando le fondamentali delle grandezze tensione e corrente.
Seguendo lo schema logico di figura 4-5, si è arrivati a determinare l’andamento in funzione della frequenza, nell’intervallo 10 Hz – 10 mHz, del modulo e della fase dell’impedenza operazionale.
I risultati ottenuti con i test in frequenza sono mostrati nelle figure 4-6 ed 4-7.
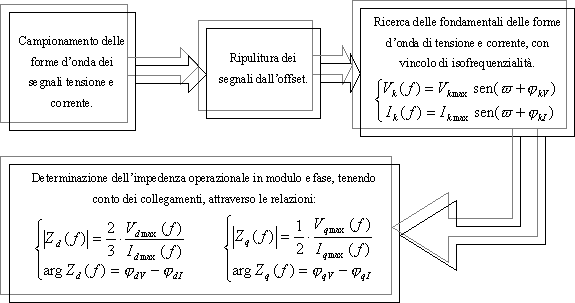
Figura 4-5. Schema logico seguito per la determinazione dell’impedenza operazionale in assi d e q, nell’intervallo di frequenza tra 10 Hz e 10 mHz.
Dopo aver effettuato questa prova si è cercato, utilizzando l’impedenzimetro vettoriale, ad analizzare il comportamento del motore per valori di frequenza fino ad 1 MHz . La figura 4-8 mostra l’andamento grafico dei risultati ottenuti con tale prova.
Analizzando tale figura si può osservare come per valori di frequenza superiori ai 20 kHz, il comportamento del motore è caratterizzato dalla presenza di capacità parassite. Si possono, infatti, notare due picchi di risonanza dovuti alla presenza di coppie di poli e zeri complessi e coniugati che entrano in gioco a quelle frequenze, e da attribuirsi sicuramente alle capacità parassite.
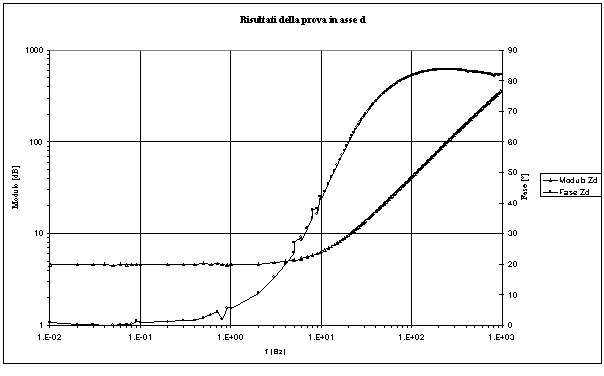
Figura 4-6. Andamento grafico del modulo e della fase dell’impedenza in asse d, in funzione della frequenza.
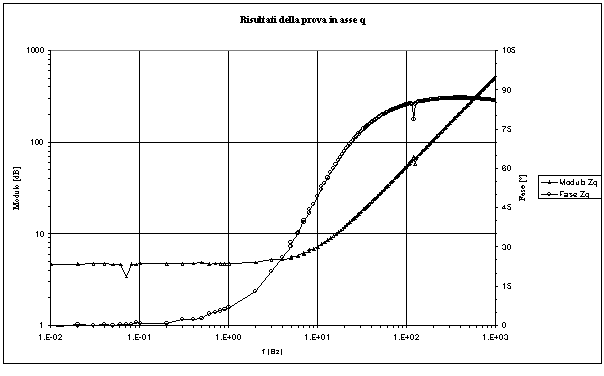
Figura 4-7. Andamento grafico del modulo e della fase dell’impedenza in asse q, in funzione della frequenza.
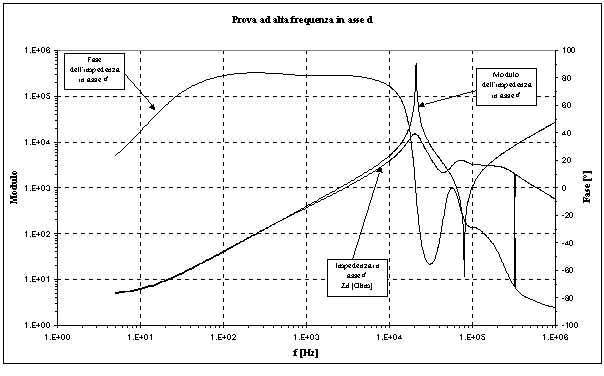
Figura 4-8. Risposta (in asse d) del motore per frequenze fino ad 1 MHz.
4.4 Elaborazione delle misure e ricerca del circuito equivalente
I grafici riportati nelle figure 4-6 e 4-7 altro non sono che i diagrammi di Bode della impedenza operazionale del motore in assi d e q. In particolare è possibile osservare su entrambi gli assi, in prossimità dei 10 Hz, la presenza di uno zero. Per la ricerca del modello della macchina, si è cercato di approssimare la funzione di trasferimento dell’impedenza operazionale con una funzione del tipo:
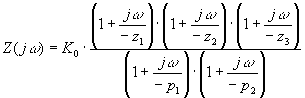 (4-3)
(4-3)
Esprimendo la (4-3) nella forma semplificata (4-4), ed ottimizzando con il metodo dei minimi quadrati si vede che il contributo di due coppie polo-zero è trascurabile, in quanto i loro valori sono molto prossimi. La tabella 4-1 riporta tali valori.
![]() (4-4)
(4-4)
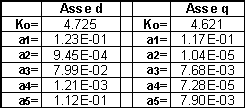
Tabella 4-1. Valori determinati per poli e zeri utilizzando il modello con tre zeri e due poli.
Abbiamo quindi proceduto ad una ulteriore ottimizzazione utilizzando una funzione contenente un solo zero:
![]() (4-5)
(4-5)
Come c’era d’aspettarsi tale funzione approssimava molto bene l’andamento dell’impedenza operazionale misurata, soprattutto per valori di frequenza inferiori ai 100 Hz.
Dai valori di ![]() ,
, ![]() ed
ed ![]() , ricordando la definizione di impedenza:
, ricordando la definizione di impedenza:
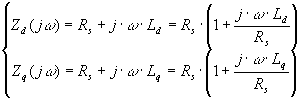 (4-6)
(4-6)
è possibile determinare uguagliando la (4-5) e la (4-6) i valori di ![]() ed
ed ![]() , in particolare:
, in particolare:
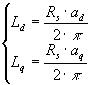 (4-7)
(4-7)
La tabella 4-2 riporta i valori determinati con tale procedimento.
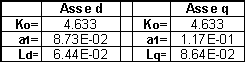
Tabella 4-2. Valori determinati per poli e zeri utilizzando il modello con un solo zero.
In questa prova il valore di ![]() è stato imposto uguale al valore della resistenza di fase di statore, in quanto dall’analisi dei risultati della tabella 4-1 si vede chiaramente che tale valore è molto vicino al valore misurato della resistenza di fase (si veda paragrafo 5-2). Questo è facilmente spiegabile anche per via teorica, in quanto nella (4-5)
è stato imposto uguale al valore della resistenza di fase di statore, in quanto dall’analisi dei risultati della tabella 4-1 si vede chiaramente che tale valore è molto vicino al valore misurato della resistenza di fase (si veda paragrafo 5-2). Questo è facilmente spiegabile anche per via teorica, in quanto nella (4-5) ![]() rappresenta il valore di Z a frequenza nulla, quindi una resistenza.
rappresenta il valore di Z a frequenza nulla, quindi una resistenza.
Le figure 4-9 ed 4-10 riportano gli andamenti grafici dell’impedenza operazionale in assi d e q misurati, ed i relativi andamenti ottenuti utilizzando il modello con un solo zero. Dalle figure è possibile osservare la buona approssimazione dei dati misurati ottenuta con tale modello.
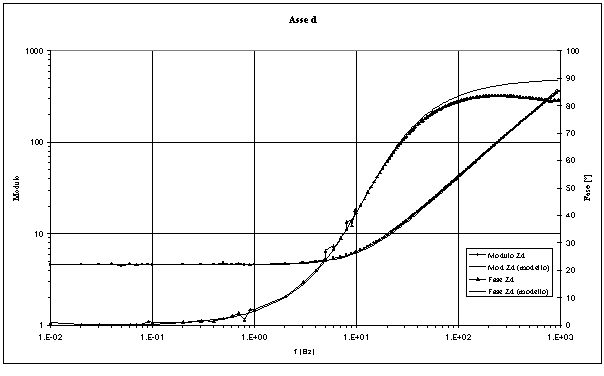
Figura 4-9. Il grafico riporta i risultati ottenuti sperimentalmente ed i risultati ottenuti con l’utilizzo del modello con un solo zero.
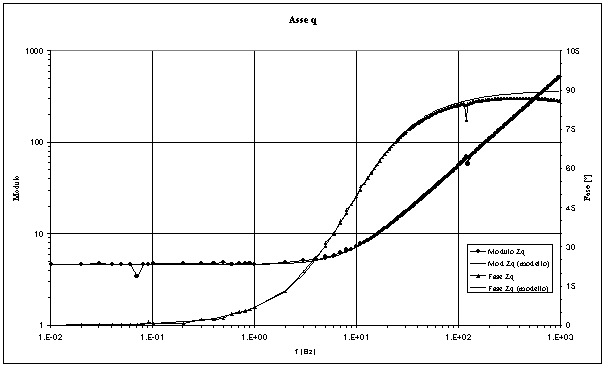
Figura 4-10. Il grafico riporta i risultati ottenuti sperimentalmente ed i risultati ottenuti con l’utilizzo del modello con un solo zero.
Siamo ora in grado di dare alla macchina un circuito equivalente. Nella figura 4-11 è riportato il modello in assi d e q per il prototipo AFIPM.
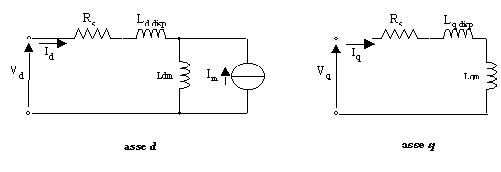
Figura 4-11. Circuito elettrico equivalente della macchina AFIPM i assi d e q.
In realtà con le misure effettuate non si è realmente risaliti ai valori di ![]() ed
ed ![]() in quanto non è facile separare il flusso disperso, a cui si riferisce la
in quanto non è facile separare il flusso disperso, a cui si riferisce la ![]() , dal flusso di magnetizzazione a cui si riferisce la
, dal flusso di magnetizzazione a cui si riferisce la ![]() . Si può quindi dire che i valori di induttanza
. Si può quindi dire che i valori di induttanza ![]() ed
ed ![]() calcolati, rappresentano la somma di
calcolati, rappresentano la somma di ![]() ed
ed ![]() sui due assi d e q.
sui due assi d e q.
Dall’analisi del circuito equivalente si può notare la mancanza dei rami smorzatori che tengono conto degli effetti delle correnti parassite. Questo può essere giustificabile se si pensa che il rotore del prototipo non è stato realizzato con lamierini in ferro ma utilizzando delle ferriti, che per come sono fatte non consentono la circolazione di significative correnti parassite. Nel circuito equivalente non si è inoltre tenuto conto dei generatori di tensione ![]() ed
ed ![]() , rispettivamente per gli assi d e q, in quanto le prove sono state effettuate a motore fermo, quindi
, rispettivamente per gli assi d e q, in quanto le prove sono state effettuate a motore fermo, quindi ![]() .
.
Prova di Risposta nel Tempo
5.1 Introduzione
Con questa prova si vuole avere una conferma del modello e dei parametri determinati con la prova in frequenza. A differenza dei test in frequenza questa prova richiede un ridottissimo tempo di esecuzione, inoltre per alimentare il motore si sono utilizzati segnali di notevole potenza. Questo va senz’altro a garanzia di una minore sensibilità ai disturbi delle forme d’onda campionate e quindi dei parametri calcolati.
In questa prova di particolare importanza è la conoscenza del valore della resistenza di fase degli avvolgimenti di statore alle varie temperature di misura. Ciò in quanto il procedimento di ottimizzazione utilizzato richiede, oltre alla conoscenza dei valori di tensione e di corrente nei vari istanti, anche la conoscenza del valore di tale resistenza.
In questo capitolo si cercherà di illustrare con maggiore dettaglio le misure effettuate e si analizzeranno i risultati ottenuti, cercando di spiegare i motivi che hanno portato a risultati diversi.
5.2 Misura della resistenza di fase
Come accennato nell’introduzione, la misura corretta della resistenza degli avvolgimenti di statore ha una particolare importanza ai fini della determinazione dei parametri del motore. La misura di resistenza è stata condotta con il metodo volt-amperometrico, rilevando la temperatura degli avvolgimenti durante la misura. Nella tabella 5-1 sono riportati i risultati delle misure della resistenza. Vista la piccolissima differenza tra i valori di resistenza delle tre fasi, si è considerato un valore unico per le resistenze dei tre avvolgimenti (![]() a
a ![]() ).
).
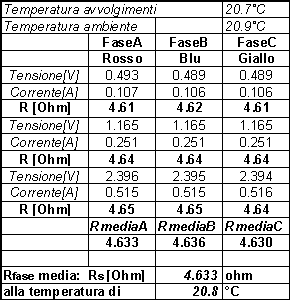
Tabella 5-1. Risultati ottenuti della misura di resistenza con il metodo volt-amperometrico.
Per tenere conto delle diverse temperature a cui i vari test si sono svolti si è effettuato, di volta in volta, il riporto della resistenza alla temperatura di prova mediante la relazione:
![]() (5-1)
(5-1)
dove ![]() e
e ![]() sono rispettivamente i valori di resistenza e temperatura alla quale si esegue il test, mentre
sono rispettivamente i valori di resistenza e temperatura alla quale si esegue il test, mentre ![]() e
e ![]() sono rispettivamente i valori di resistenza e temperatura alla quale si è misurata la resistenza (
sono rispettivamente i valori di resistenza e temperatura alla quale si è misurata la resistenza (![]() e
e ![]() ).
).
5.3 Risposta, in assi d e q, ad un ingresso a gradino
In questa prova si procede alla determinazione dei parametri del motore analizzando la risposta al gradino sui due assi d e q. Volendo avere una conferma del modello trovato con i test in frequenza, si è preferito non ripetere il posizionamento del motore in asse d, ma utilizzare lo stesso posizionamento utilizzato per la prova in frequenza. Ciò in quanto, non è possibile eliminare completamente l’errore di posizionamento e volendo, comunque, dei risultati confrontabili con quelli ottenuti nella prova in frequenza.
Alimentato il motore, prima in asse d e poi in asse q secondo gli schemi riportati in figura 5-1, si è proceduto all’acquisizione delle forme d’onda di tensione e di corrente mediante l’utilizzo di un campionatore (oscilloscopio Le Croy). Su ogni asse si è proceduto al campionamento dei segnali per valori di corrente di 1 A, 2 A, 3 A, 4 A, 5 A.
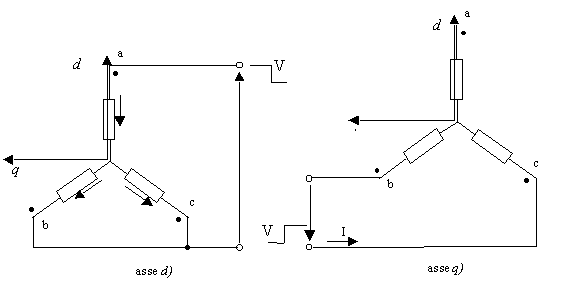
Figura 5-1. Schemi utilizzati per l’alimentazione del motore AFIPM in assi d e q.
Le figure 5-2 ed 5-3 riportano un esempio di risposta al gradino, rispettivamente in asse d ed in asse q, del motore.
5.4 Determinazione dei parametri del motore
Note le risposte al gradino, in assi d e q del motore, e utilizzando il modello ad un solo zero ottenuto dalla prova in frequenza, è possibile risalire ai parametri del motore.
Per fare ciò scriviamo le equazioni del modello in assi d e q tenendo conto dei collegamenti:
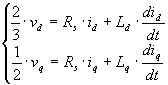 (5-2)
(5-2)
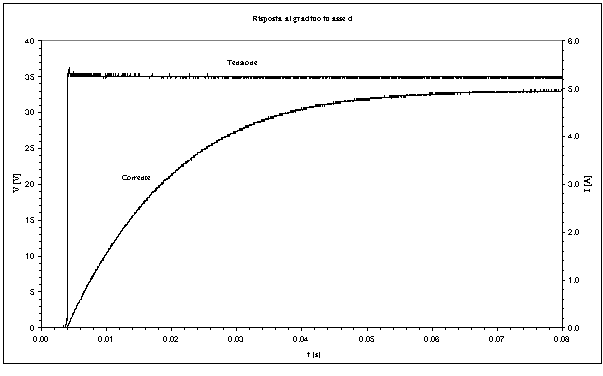
Figura 5-2. Andamento grafico della risposta al gradino per la macchina AFIPM relativa all’asse d (dati misurati).
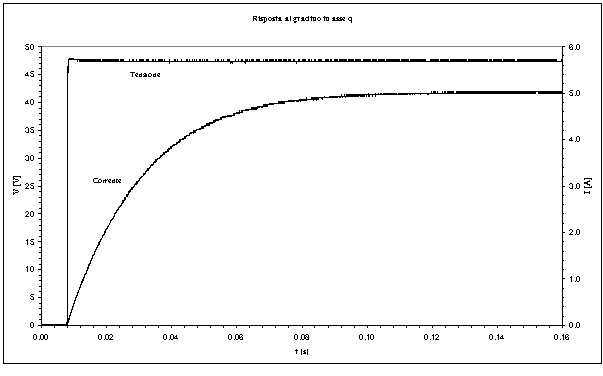
Figura 5-3. Andamento grafico della risposta al gradino per la macchina AFIPM relativa all’asse q (dati misurati).
Visto che le forme d’onda sono campionate, le grandezze sono date da un insieme, ordinato rispetto al tempo, di numeri che rappresentano tensione e corrente negli istanti di campionamento. Dalla (5-2) scritta in forma numerica, è possibile calcolare il valore assunto dalla corrente nell’istante successivo a quello considerato, mediante le relazioni (5-3).
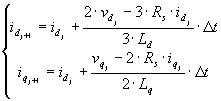 (5-3)
(5-3)
Determinata la colonna delle correnti calcolate, è possibile risalire ai valori di ![]() ed
ed ![]() ottimizzando con il metodo dei minimi quadrati rispetto ai parametri cercati.
ottimizzando con il metodo dei minimi quadrati rispetto ai parametri cercati.
La tabella 5-2 riporta i valori calcolati, seguendo questo procedimento, dei parametri ![]() ed
ed ![]() del motore.
del motore.
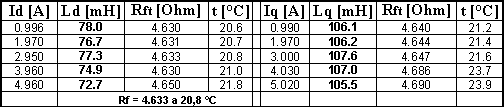
Tabella 5-2. Tabella riassuntiva dei parametri del motore AFIPM determinati con la prova di risposta al gradino.
Determinati i parametri del modello, e notata la notevole differenza dei valori determinati con i test in frequenza, si è proceduto ad una verifica del modello.
Tale verifica altro non era che un confronto grafico tra la risposta al gradino ottenuta sperimentalmente e quella ottenuta numericamente utilizzando il modello R-L della macchina.
Nelle figure 5-4 ed 5-5 sono riportati, rispettivamente per gli assi d e q, gli andamenti grafici della risposta al gradino misurata e calcolata.
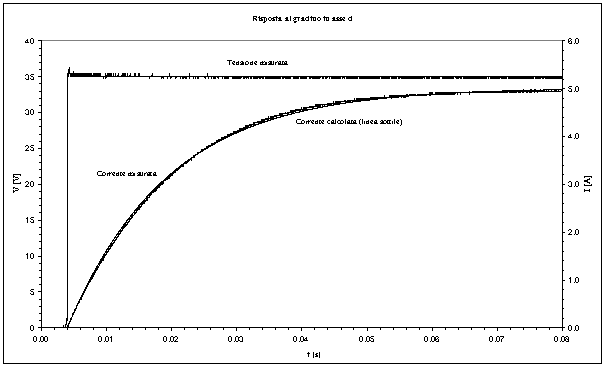
Figura 5-4. Confronto tra la risposta al gradino in asse d misurata e quella calcolata utilizzando il modello R-L, si può notare la buona approssimazione del modello in asse d.
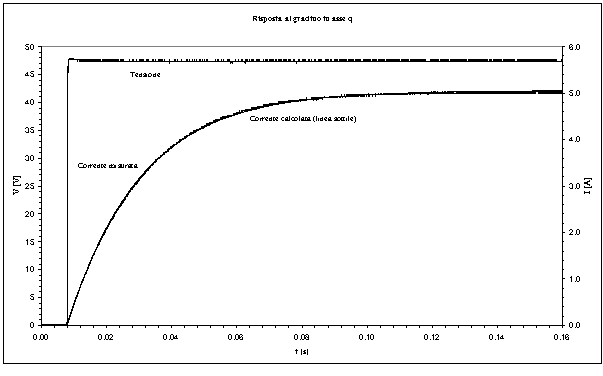
Figura 5-5. Confronto tra la risposta al gradino in asse q misurata e quella calcolata utilizzando il modello R-L, si può notare l’ottima approssimazione del modello in asse q.
5.5 Analisi dei risultati ottenuti
Analizzando le figure 5-4 ed 5-5 e immediato constatare che il modello R-L adottato per il motore, pur assumendo valori diversi per i parametri rispetto a quelli determinati con la prova in frequenza, approssima molto bene il comportamento reale della macchina. Questo può significare che nonostante il modello trovato sia idoneo a rappresentare il comportamento della macchina, i parametri determinati con le prove in frequenza e nel tempo, si riferiscono a condizioni di funzionamento diverse. Considerando i livelli di potenza dei segnali utilizzati come ingresso nelle due prove, si capisce che i parametri sono stati determinati con due prove in cui i materiali erano portati a lavorare in modo nettamente diverso.
Per avere una conferma dell’ipotesi fatta, non avendo a disposizione informazioni sul comportamento delle ferriti in presenza di polarizzazione e di piccoli segnali, si sono effettuate delle prove su un campione di ferrite allo scopo di trarre maggiori informazioni sul comportamento magnetico del materiale. Questa prova è descritta in dettaglio nel capitolo 9.
I risultati delle misure magnetiche sulle ferriti hanno confermato che, se il materiale viene fatto lavorare in condizione di polarizzazione (dovuta alla presenza dei magneti sul rotore) e di piccolo segnale come appunto si verifica nella prova in frequenza, la permeabilità del materiale scende notevolmente, ciò influisce direttamente sul valore delle induttanze ![]() ed
ed ![]() . Questo si può spiegare pensando che in presenza di polarizzazione il ciclo d’isteresi compiuto dal materiale non è simmetrico rispetto all’origine, inoltre se il segnale è piccolo tale ciclo è molto ridotto, questo porta a dire che non è giusto considerare in questo caso la permeabilità normale, ma bisogna considerare la permeabilità differenziale del materiale. Quanto detto è illustrato graficamente in figura 5-6.
. Questo si può spiegare pensando che in presenza di polarizzazione il ciclo d’isteresi compiuto dal materiale non è simmetrico rispetto all’origine, inoltre se il segnale è piccolo tale ciclo è molto ridotto, questo porta a dire che non è giusto considerare in questo caso la permeabilità normale, ma bisogna considerare la permeabilità differenziale del materiale. Quanto detto è illustrato graficamente in figura 5-6.
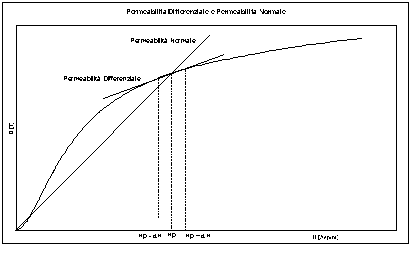
Figura 5-6. Rappresentazione grafica della permeabilità normale e differenziale.
Si riporta in figura 5-7, un grafico riassuntivo dei risultati ottenuti nelle misure magnetiche. Tali risultati sono in buon accordo con i dati dichiarati sul catalogo del produttore.
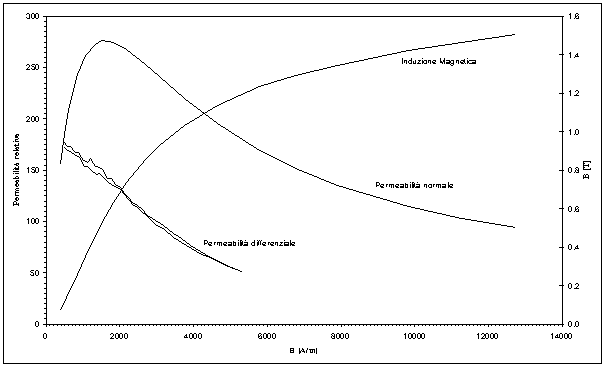
Figura 5-7. Caratteristiche magnetiche delle ferriti utilizzate nel prototipo AFIPM (dati sperimentali).
Per maggiori dettagli sulle caratteristiche magnetiche delle ferriti utilizzate nella realizzazione del prototipo si rimanda al capitolo 9.