Modulo 8 – Dal Problema al Programma

Scopo del modulo

Conoscere alcuni concetti fondamentali dell’informatica: algoritmo, automa, linguaggio formale.
Essere in grado di cogliere l’intreccio tra alcuni risultati della matematica e della logica dei primi decenni del secolo scorso ed i successivi sviluppi e applicazioni che questi hanno avuto in campo informatico.Il modulo non mira al raggiungimento di specifiche abilità operative, ma a costituire quel quadro di conoscenze che consenta di cogliere l’intreccio tra alcuni risultati della matematica e della logica dei primi decenni del secolo scorso e i successivi sviluppi e applicazioni che questi hanno avuto in campo informatico.

INDICE

8.1 Problemi e Algoritmi

8.1.1. Introduzione intuitiva del concetto di problema

8.1.2. Cenni sulle strategie per la risoluzione dei problemi

8.1.3. Soluzione di un problema

8.1.4. Gli algoritmi

8.1.4a I Diagrammi a Blocchi

8.1.4b Esempi di algoritmi rappresentati mediante diagrammi a blocchi

8.1.4c Il Linguaggio di progetto

8.1.4d Esempi di algoritmi rappresentati mediante Linguaggio di progetto

8.2 Automi Esecutori

8.2.1. Caratteristiche di un automa e meccanizzazione della soluzione di un problema

8.2.1a Il concetto di sistema

8.2.1b Il concetto di modello

8.2.1c Il concetto di automa

8.2.1d Esempi di automi a stati finiti

8.2.2. Automi e classi di problemi

8.3 Linguaggi

8.3.1. Sintassi e semantica dei linguaggi formali

8.3.1a I linguaggi nella comunicazione uomo-macchina

8.3.2. Linguaggi e automi

8.3.2a Rassegna dei principali software

8.3.3. Introduzione ai linguaggi di programmazione

8.3.4. Rassegna sui Principali Linguaggi

Approfondimento 1 - Aggregazione di sottosistemi

Approfondimento 2 – La macchina di Turing

Approfondimento 3 – Categorie dei linguaggi evoluti

Approfondimento 4 – Le istruzioni di controllo

Indice delle Figure

BIBLIOGRAFIA

8.1 Problemi e Algoritmi

Obiettivi (estratto dalla C.M. n.55 del 21-5-2002):

· Riconoscere e analizzare una situazione problematica.

· Conoscere alcuni dei procedimenti di riduzione di problemi complessi a sottoproblemi.

· Riconoscere le caratteristiche che una procedura risolutiva deve possedere.

· Rappresentare una procedura rigorosa e generale di soluzione di un problema.

8.1.1 Introduzione intuitiva del concetto di problema

Col termine problema o situazione problematica s’indica una situazione che pone delle domande cui si devono dare risposte. Risolvere il problema vuol dire uscire da tale situazione.

Un problema consta dei seguenti elementi:

· I dati, ossia ciò che è noto, l’istanza che si deve affrontare e che possiamo indicare col termine input.

· I risultati, ossia ciò che si deve determinare, gli elementi incogniti la cui determinazione fornisce l’output.

· Le condizioni, che sono in generale le limitazioni cui devono soggiacere i risultati.

La formulazione del problema determina la strategia risolutiva migliore da adottare per risolverlo.

Per cogliere il collegamento tra la struttura di un problema ed i metodi risolutivi per esso adottati, è opportuno tenere conto della seguente ripartizione dei vari tipi di problemi in classi:

· Problemi di decisione, in cui l’output è fornito dal valore vero o falso a seconda che l’input soddisfi o meno una determinata proprietà.

· Problemi di ricerca, in cui, nello spazio delle soluzioni possibili (spazio di ricerca), si vuole determinare quella soluzione che soddisfa le condizioni poste dal problema, che viene detta soluzione ammissibile.

· Problemi di ottimizzazione, in cui alle soluzioni ammissibili è associata una misura e si deve determinare la soluzione ammissibile la cui misura è massima o minima.

8.1.2. Cenni sulle strategie per la risoluzione dei problemi

Il primo passo da compiere è analizzare il problema col quale si ha a che fare.

Per compiere l’analisi di un problema il risolutore deve:

•interpretare l’enunciato del problema e definire gli obiettivi da realizzare;

•individuare i dati del problema e costruire un modello opportuno (modello è una rappresentazione della realtà privata degli aspetti superflui alla soluzione del problema);

•descrivere il procedimento risolutivo individuando le operazioni da compiere sui dati iniziali per ottenere i risultati finali;

•eseguire nell’ordine le operazioni descritte nel processo risolutivo (il risolutore in questa fase è detto esecutore);

•verificare se i risultati ottenuti rispondono alle finalità del problema reale (attendibilità).

Le fasi sopraelencate sono riassunte dallo schema che segue.

Fig.1 Analisi di un problema

La prima fase dell’analisi di un problema, ossia la definizione dell’obiettivo da raggiungere, può essere realizzata attraverso processi di affinamento sempre più dettagliati. Si tratta di scomporre un problema complesso in sottoproblemi più semplici, utilizzando la tecnica del top-down:

· il problema viene esaminato nelle direttrici generali;

· scomposto in sottoproblemi;

· di ciascun sottoproblema si determinano le operazioni specifiche;

· esso viene scomposto in ulteriori sotto-sottoproblemi, fino a giungere alle operazioni elementari.

La strategia risolutiva sopra descritta è illustrata dallo schema seguente:

Fig. 2 Tecnica del top-down

8.1.3. Soluzione di un problema

Non esistono metodi precisi che possano essere indicati per risolvere un problema, in quanto ogni problema va affrontato nella propria specificità e la sua soluzione dipende dalle conoscenze che si possiedono intorno a quel problema ed alle tecniche per risolverlo.

Compiuto il primo passo, quello dell’analisi del problema, si può far scaturire da essa una descrizione discorsiva del problema e delle varie fasi del processo risolutivo individuato.

L’esplicitazione di tale descrizione può avvenire mediante la formalizzazione dei passi elementari da effettuare, che può essere realizzata tramite una Pseudocodifica (Notazione Lineare Strutturata) o mediante la tecnica del Diagramma a Blocchi.

8.1.4. Gli algoritmi

Si dice algoritmo un insieme di istruzioni che definiscono una sequenza di operazioni mediante le quali si risolvono tutti i problemi di una determinata classe.

L’algoritmo deve essere:

•finito, costituito cioè da un numero limitato di passi (le istruzioni sono in numero finito e vengono eseguite un numero finito di volte);

•definito, ogni istruzione deve consentire un’interpretazione univoca;

•eseguibile, cioè la sua esecuzione deve essere possibile con gli strumenti di cui si dispone;

•deterministico, ad ogni passo deve essere definita una ed una sola operazione successiva.

Le caratteristiche sopraelencate caratterizzano un processo automatizzabile, che esclude la componente intuitiva propria dell’elaborazione governata dall’uomo.

Le istruzioni devono essere espresse informa comprensibile all’esecutore (cioè interpretabili dal sistema di elaborazione) e devono descrivere le azioni da compiere al livello di dettaglio delle capacità elementari dell’esecutore.

Per facilitare la stesura dell’algoritmo si ricorre a rappresentazioni grafiche e formalizzate, quali ad esempio i Diagrammi a Blocchi o il Linguaggio di progetto.

8.1.4.a I Diagrammi a Blocchi

Tra le tecniche utilizzate per rappresentare in maniera chiara e sintetica la struttura degli algoritmi, quella del Diagramma a Blocchi , anche detto flow-chart, ha il pregio di evidenziare visivamente l’avanzamento in sequenza e le varie strutture che compongono l’algoritmo.

Questa tecnica si basa sull’osservazione che le istruzioni di un qualunque algoritmo sono di uno dei seguenti tipi:

· istruzioni di calcolo o di elaborazione, che descrivono un’azione da compiere necessariamente dopo la precedente e prima della seguente nell’elenco ordinato;

· condizioni che pongono una domanda cui si può rispondere sì/no oppure vero/falso e che, a seconda della risposta, indicano due diverse azioni da compiere.

Le due tipologie di istruzioni vengono rappresentate convenzionalmente con le forme geometriche rettangolo e rombo, la logica di sequenza viene data da frecce che congiungono i vari blocchi nel senso di avanzamento dell’esecuzione.

Per le istruzioni di input e di output si usa un parallelogramma, per identificare l’inizio e la fine della sequenza di istruzioni si usa l’ellisse, la necessità di mutare la sequenza d’esecuzione passando ad un’istruzione che non sia quella immediatamente successiva (istruzioni di salto) è resa graficamente mediante le frecce.

Per meglio chiarire l’uso di questa tecnica di rappresentazione si vedano gli esempi di diagrammi a blocchi.

8.1.4.b Esempi di algoritmi rappresentati mediante diagrammi a blocchi

ALGORITMO 1 - Somma di una sequenza di numeri

Indicando con a_i il generico elemento da sommare, la formula matematica generale è S = a₁+ a₂ +…+ a_n . Bisogna fornire in input all’elaboratore i singoli valori a_i ed il numero n di tali valori. L’algoritmo utilizza una struttura iterativa, ossia un blocco d’istruzioni viene ripetuto un numero finito di volte.

Utilizzeremo una variabile N per l’input di n e per contare quante volte si deve ripetere l’iterazione; il valore di N si decrementa di un’unità nell’ambito dell’iterazione e l’iterazione termina quando N raggiunge il valore zero. La variabile A è usata per gli input degli a_i, S per le somme parziali e totale.

Fig. 3 Algoritmo 1 – Diagramma a blocchi

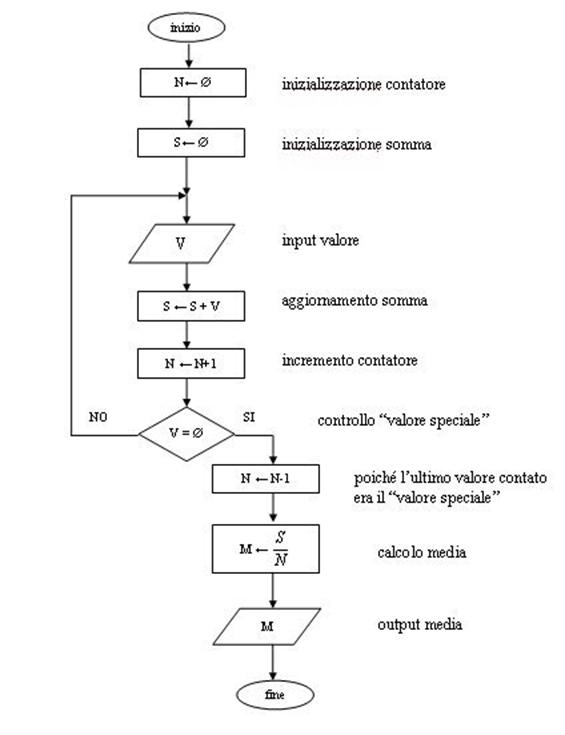
ALGORITMO 2 – Calcolo della media aritmetica di una sequenza di valori numerici

La formula matematica è M = .

Si consente all’utente di introdurre un numero qualsiasi di dati, utilizzando un valore speciale (lo zero) per indicare la fine della sequenza di input; l’algoritmo conta quanti elementi vengono introdotti.

Fig.4 Algoritmo 2 – Diagramma a blocchi

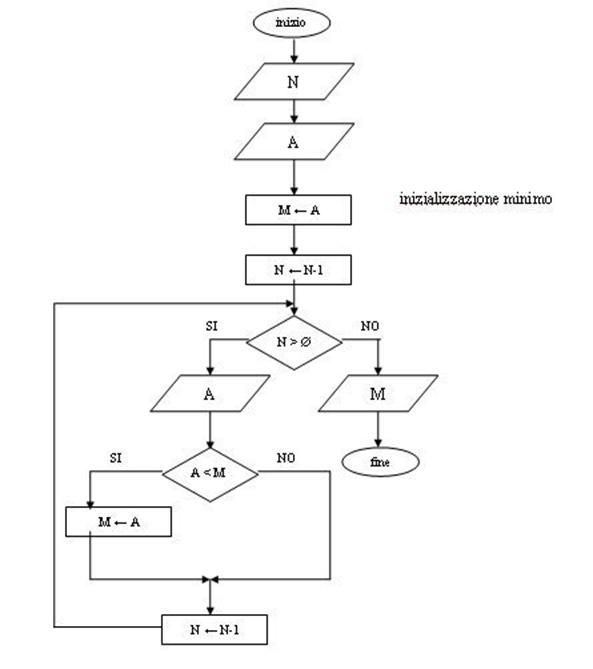
ALGORITMO 3 – Ricerca del minimo di una sequenza di valori numerici

Indicati con a_i i valori sui quali si deve effettuare la ricerca, si può risolvere il problema con un algoritmo iterativo che effettua confronti successivi: M₁=min(a₁,a₂); M₂=min(M₁,a₃); M₃=min(M₂,a₄);…; M_n-1=min(M_n-2, a_n). Al termine degli n-1 confronti, M_n-1 coincide col minimo cercato. La variabile A è usata per gli input degli a_i . N è il contatore delle iterazioni.

Fig. 5 Algoritmo 3 – Diagramma a blocchi

Esercizio proposto: in modo analogo, realizzare il diagramma per l’algoritmo di ricerca del massimo di una sequenza di valori.

ALGORITMO 4 – Ordinamento per scambio di una sequenza di numeri in modo crescente

Indicati con a_i i valori da ordinare, deve risultare a₁≤a₂≤a₃≤…≤a_n-1≤a_n . Si può sfruttare l’algoritmo per la ricerca del minimo, utilizzando un vettore per memorizzare gli n valori numerici da ordinare. Si inizierà applicando l’algoritmo di ricerca del minimo su tutti gli elementi del vettore e spostando il minimo in prima posizione, si procederà analogamente sui rimanenti n-1 elementi e il minimo tra essi si sposterà in seconda posizione, poi si ripeterà la procedura sui restanti n-2 elementi del vettore e così via. Il diagramma a blocchi illustra l’algoritmo in questione, supponendo di avere già a disposizione il vettore V(i) con i suoi n valori.

Fig. 6 Algoritmo 4 – Diagramma a blocchi

Esercizio proposto: in modo analogo, realizzare il diagramma per l’algoritmo di ordinamento per scambio di una sequenza di numeri in modo decrescente.

8.1.4.c Il Linguaggio di progetto

Un algoritmo può essere rappresentato anche mediante un linguaggio speciale che descrive le istruzioni e la logica di avanzamento dell’esecuzione con frasi anziché con un diagramma. Si parla in tal caso di pseudocodifica o notazione lineare strutturata.

Tale linguaggio formale, detto linguaggio di progetto, assomiglia al linguaggio naturale, ma è privo di ambiguità e segue regole prive di eccezioni. Esso utilizza parole riservate, spesso tratte dalla lingua inglese, mediante le quali vengono espressi i diversi tipi di istruzioni.

Gli esempi mostrano l’utilizzo di questa tecnica, in particolare mediante la codifica in linguaggio pseudopascal, cosiddetto perché simile al linguaggio di programmazione Pascal.

8.1.4.d Esempi di algoritmi rappresentati mediante Linguaggio di progetto

ALGORITMO 1 - Somma di una sequenza di numeri

Riguardo i dettagli dell’algoritmo si rimanda a quanto detto nella sua codifica mediante diagramma a blocchi.

Pseudocodifica algoritmo 1:

ALGORITMO 2 – Calcolo della media aritmetica di una sequenza di valori numerici

Riguardo i dettagli dell’algoritmo si rimanda a quanto detto nella sua codifica mediante diagramma a blocchi.

Pseudocodifica algoritmo 2:

ALGORITMO 3 – Ricerca del minimo di una sequenza di valori numerici

Riguardo i dettagli dell’algoritmo si rimanda a quanto detto nella sua codifica mediante diagramma a blocchi.

Pseudocodifica algoritmo3:

ALGORITMO 4 – Ordinamento per scambio di una sequenza di numeri in modo crescente

Riguardo i dettagli dell’algoritmo si rimanda a quanto detto nella sua codifica mediante diagramma a blocchi.

Pseudocodifica algoritmo 4:

8.2 Automi Esecutori

Obiettivi (estratto dalla C.M. n.55 del 21-5-2002):

· Essere in grado di costruire una procedura risolutiva di un problema sfruttando opportunamente le peculiarità dell’esecutore.

· Comprendere la rilevanza le caratteristiche di base di un automa per la soluzione di classi di problemi.

8.2.1. Caratteristiche di un automa e meccanizzazione della soluzione di un problema

La risoluzione di un problema è un processo di manipolazione di informazioni finalizzato a generare nuove informazioni.

Per informazione intendiamo un elemento di conoscenza significativa, che può essere utilizzata immediatamente oppure conservata per un utilizzo futuro.

Le attività cui si dà luogo per risolvere il problema possono essere distinte in:

· attività “intelligenti“ di elaborazione

· attività “routinarie” di esecuzione

Mentre il primo ruolo è riservato alla mente umana, il ruolo routinario viene delegato a strumenti capaci di svolgere in modo rapido ed esatto le operazioni logico-matematiche.

Tali strumenti sono macchine, dette automi, che compiono attività complesse in cui sono riconoscibili elementi propri delle attività superiori del comportamento umano. Queste macchine possono essere programmate per svolgere diverse mansioni e per modificare le proprie azioni in relazione ai mutamenti ambientali.

8.2.1.a Il concetto di sistema

Si dice sistema un insieme di elementi che interagiscono tra loro in modo da formare una unità ch,e al verificarsi di un dato evento (azione) proveniente dall’ambiente esterno (ecosistema), produce una risposta definita.

La risposta del sistema (output) agli input esterni dipende anche dallo stato in cui il sistema si trova in quell’istante. Un sistema è dotato di memoria, la sua storia è conservata nel suo stato.

Fig. 7 Rappresentazione schematica di un sistema:

Esempio: un ascensore che si trovi al piano terra, quando l’utente preme il pulsante 2 sale di due piani; se l’utente preme ancora il pulsante 2 una volta arrivato al secondo piano, l’ascensore non si muove. Il sistema ha prodotto uscite diverse in quanto si trovava in stati diversi.

Al suo interno, gli elementi detti sottosistemi, si comportano analogamente, ricevendo ingressi e fornendo uscite (risultati parziali rispetto allo scopo globale del sistema).

Fig. 8 Sistema e sottosistemi

8.2.1.b Il concetto di modello

Nella rappresentazione dei sistemi si devono descrivere gli input, gli output e i processi avviati dagli input. Tale rappresentazione di un sistema o di un processo deve permetterne lo studio senza realizzarlo fisicamente.

Un modello è uno schema teorico elaborato in molte discipline per rappresentare gli elementi fondamentali di fenomeni o enti.

In base all’uso i modelli vengono detti:

· modelli descrittivi o statici: riproducono con eventuali semplificazioni la realtà, senza presupporre l’uso che ne verrà fatto

· modelli predittivi: danno gli elementi di una certa realtà necessari per prevederne l’evoluzione, lasciando spazio ad eventuali scelte

· modelli prescrittivi: impongono un particolare comportamento in previsione dell’obiettivo da raggiungere

· modelli simbolici o matematici: danno una rappresentazione astratta della realtà cui si riferiscono, mediante un insieme di equazioni e/o disequazioni che legano le grandezze coinvolte

· modelli analogici: danno una rappresentazione fedele della realtà, tipici sono i modelli in scala ridotta, che riproducono qualitativamente un sistema pur riducendone proporzionalmente la dimensione

L’avvento degli elaboratori veloci ha reso possibile lo studio di sistemi complessi (sistemi sociali, sistemi di produzione,sistemi fisici ,…) effettuando in laboratorio esperimenti controllati attraverso gli elaboratori elettronici.

8.2.1.c Il concetto di automa

Un automa è un sistema dinamico, invariante, discreto nell’avanzamento e nelle interazioni.

· dinamico: evolve nel tempo passando da uno stato all’altro in funzione dei segnali d’ingresso e dello stato precedente;

· invariante: a parità di condizioni iniziali il comportamento del sistema è sempre lo stesso;

· discreto: le variabili d’ingresso, di stato, d’uscita, possono assumere solo valori discreti.

In termini formali, si definisce automa a stati finiti un sistema A = {I, U, S, f, g }, dove

· I = {i₁, i₂, …i_n} insieme finito dei possibili ingressi

· U = {u₁, u₂, …, u_m} insieme finito di possibili uscite

· S = {s₁, s₂, …, s_h} insieme finito di stati

· f = I × S U funzione delle uscite, che collega l’uscita al valore attuale dell’ingresso e dello stato, u_t=f (s_t, i_t)

· g = I ×S S funzione di transizione degli stati interni successivi, che collega lo stato nell’istante successivo al valore attuale dell’ingresso e dello stato, s_t+1=g(s_t, i_t)

L’espressione a stati finiti accanto al termine automa distingue quegli automi in cui anche l’insieme S è finito, mentre I ed U lo sono sempre.

Le funzioni f (delle uscite) e g (di transizione dello stato successivo) possono essere rappresentate mediante:

1. Tabelle di transizione, tabelle a doppia entrata in cui il numero delle righe è pari al numero degli stati e quello delle colonne è pari al numero degli ingressi.

2. Grafi di transizione, costituiti da cerchi (nodi) in numero pari agli stati, da ciascuno dei quali partono tanti archi quanti sono gli ingressi. Se le uscite sono riportate sugli archi sotto gli ingressi si dice automa di Mealy, se le uscite sono riportate all’interno dei nodi sotto lo stato si dice automa di Moore.

8.2.1.d Esempi di automi a stati finiti

Ascensore

Un ascensore di un palazzo a due piani accetta la richiesta del piano di destinazione (terra, 1, 2) e restituisce lo spostamento desiderato (su, giù, fermo). Si tratta di un automa in cui S={Pt, 1P, 2P}, Pt= p. terra, 1P= p. primo, 2P= p. secondo; I={T, 1, 2} possibilità offerte dalla pulsantiera; U={Su, Giù, Fermo} spostamenti dell’ascensore.

Tab.1 Tabella di transizione relativa all’automa dell’esempio:

Fig. 9 Grafo di Moore relativo all’automa dell’esempio

Gettoniera

Una gettoniera, dopo l’immissione successiva di due monete, emette un gettone.

L’insieme degli ingressi è I = {m,0}, dove m rappresenta la moneta e 0 indica che non è stata introdotta alcuna moneta.

L’insieme delle uscite è U = {0,g}, dove 0 è nessuna risposta perché la macchina, ricevuta la prima moneta, è in attesa della seconda o non ha ricevuto monete, g rappresenta un gettone.

L’insieme degli stati è S = { s₁,s₂}, dove s₁ è lo stato iniziale, quando la gettoniera è in attesa della prima moneta, s₂ è lo stato di attesa della seconda moneta.

Tab.2 Matrice degli stati: ad ogni coppia ingresso-stato presente associa lo stato successivo assunto dalla macchina

Tab.3 Matrice delle uscite: ad ogni coppia ingresso-stato presente associa una risposta in uscita

Sistema di regolazione di un orologio digitale

L'orologio è munito di tre pulsanti P1, P2, P3. P1 serve per passare dallo stato in cui il display mostra ore-minuti agli stati di regolazione, P2 serve per incrementare il valore attualmente presente sul display (inc=incrementa), il tasto P3 è un tasto bistabile tra le modalità del display ore-minuti e mese-giorno.

Fig. 10 Grafo dell’orologio digitale

Automa che riconosce un identificatore

Un identificatore è costituito da una lettera seguita da altre lettere o cifre.

L’insieme degli ingressi è I={LETTERA, CIFRA}, quello delle uscite è U={IDENTIFICATORE, NON IDENTIFICATORE}, l’insieme degli stati è S={A, X }. A è lo stato iniziale di attesa dell’inserimento del primo carattere (lettera o cifra), X è lo stato finale cui s’arriva se la stringa d’ingresso è un identificatore. Se il primo carattere introdotto non è una lettera, l’automa resta nello stato A, che corrisponde all’uscita NON IDENTIFICATORE, lo stato finale X corrisponde all’uscita IDENTIFICATORE.

Fig. 11 Grafo dell’automa che riconosce un identificatore

Automa che riconosce identificatori e numeri interi

Un identificatore è costituito da una lettera seguita da altre lettere o cifre. Un numero intero è una sequenza di cifre.

L’insieme degli ingressi è I={LETTERA, CIFRA}, quello delle uscite è U={IDENTIFICATORE, NUMERO, NE’ IDENTIFICATORE NE’ NUMERO}, l’insieme degli stati è S={A, X, Y }. A è lo stato iniziale di attesa dell’inserimento del primo carattere (lettera o cifra). Lo stato finale X è quello a cui si arriva se la stringa di ingresso è un identificatore. Lo stato Y corrisponde invece ai numeri interi.

Fig. 12 Grafo dell’automa che riconosce identificatori e numeri interi

8.2.2 Automi e classi di problemi

Molte macchine che usiamo quotidianamente sono automi: la lavatrice, la lavastoviglie, l’impastatrice, i sistemi di controllo degli ascensori, i distributori automatici di bevande, i distributori automatici di benzina, i bancomat.

In ambito più specialistico ci sono automi riconoscitori di sequenze, automi analizzatori di linguaggio, automi decodificatori, automi traduttori.

I computer sono automi, particolari automi a programma, possono cioè svolgere il ruolo di un automa o di un altro dipendentemente dal programma che si manda in esecuzione.

L’uso di automi è uno strumento di astrazione molto potente per individuare la soluzione di particolari classi problemi. Attraverso la rappresentazione del grafo di un automa si analizza il suo comportamento logico-funzionale senza la necessità di una sua realizzazione fisica.

Si tratta di una tecnica adatta allo studio di quelle categorie di sistemi che non necessitano del controllo umano, ma sono “autonomi” nel procedere all’espletamento delle loro funzioni (sistemi realizzati dall’uomo per compiere lavori specifici). L’uomo che li utilizza interviene solo nel fornire i comandi in ingresso o nell’azionare pulsanti e, senza interessarsi di cosa accade al loro interno, vede solo l’effettuazione della funzione in uscita. I processi avviati dagli input sono deterministici, univoci, previsti per qualunque caso in ingresso.

Un sistema automatico è un sistema in cui la componente umana è completamente eliminata nell’ambito dei processi, che sono ben determinati e prevedibili e ogni richiesta in ingresso può attivare uno di tutti e soli i processi eseguibili dal meccanismo interno.

Approfondimento: La Macchina di Turing.

Un sistema umano, al contrario, quale ad esempio un sistema aziendale, presenta un carattere probabilistico poiché l’uomo può assolvere a funzioni anche impreviste, in numero indeterminato, utilizzando ragionamento, ma anche creatività ed intuito.

8.3 Linguaggi

Obiettivi (estratto dalla C.M. n.55 del 21-5-2002):

· Riconoscere gli elementi che concorrono a definire un linguaggio (alfabeto, parola, grammatica, ...).

· Riconoscere l’estrema varietà di automi e relativi linguaggi contemporaneamente presenti in un calcolatore: il microprocessore, il sistema operativo, il word processor, il foglio di calcolo, ecc..

· Riconoscere i linguaggi di programmazione come interfaccia per codificare algoritmi.

· Riconoscere le strutture fondamentali dei linguaggi di programmazione.

8.3.1. Sintassi e semantica dei linguaggi formali

Il linguaggio consente la comunicazione, intesa come scambio di informazioni (elementi di conoscenza significativa).

Un’informazione può:

· essere acquisita tramite rilevamento diretto di un evento reale, mediante percezione sensoriale;

· essere trasmessa intenzionalmente (messaggio) da un emittente al ricevente per mezzo di un canale.

Nel secondo caso la sorgente dell’informazione sceglie la rappresentazione più opportuna dell’informazione, affinché il messaggio sia compreso in modo univoco ed obiettivo. L’emittente è colui dal quale parte l’informazione, il mezzo che trasporta l’informazione è detto canale. Il ricevente è il destinatario dell’informazione.

La funzione fondamentale del linguaggio è quella di sostituire ad oggetti o concetti dei simboli. Ogni parola (significante) rappresenta un oggetto concreto, una persona, un ente astratto (significato).

Distinguiamo tra:

· linguaggi naturali, utilizzati nella comunicazione quotidiana tra gli esseri umani, privi di una definizione rigorosa ed in continua evoluzione, spesso presentano ambiguità ma hanno enorme potenza espressiva;

· linguaggi formali, creati dall’uomo per scopi precisi, secondo regole convenzionali esplicite che non ammettono eccezioni e non consentono sinonimi e omonimie. Il significato di una frase di tali linguaggi è sempre privo di ambiguità, è sempre possibile determinarne la correttezza (grammaticale), ma essi hanno potere espressivo limitato.

Il linguaggio è un sistema di segni, sistema in quanto i vari elementi si cui è formato funzionano insieme in un tutto unitario. I segni sono le parole (stringhe) del linguaggio, che si usano per indicare l’associazione tra un dato percepibile ed un concetto. Ogni parola (significante) rappresenta un oggetto concreto, una persona, un ente astratto che la mente umana associa al messaggio (significato).

Elementi di un linguaggio:

•alfabeto: insieme finito e non vuoto di simboli convenzionali espressi con segni tipografici detti caratteri

•sintassi: insieme finito e non vuoto delle regole mediante le quali si formano le stringhe o le frasi di un linguaggio

•semantica: insieme finito e non vuoto di significati da attribuire alle stringhe

•grammatica: insieme finito e non vuoto di tutte le regole che servono per generare un linguaggio

8.3.1.a I linguaggi nella comunicazione uomo-macchina

L’utilizzo di un linguaggio formale consente di passare da un algoritmo al corrispondente programma.

Si dice programma una sequenza di istruzioni espresse in un linguaggio formale (linguaggio di programmazione) mediante le quali si può risolvere un problema.

L’esecuzione di un programma è un evento che trasforma dati in risultati.

Dal confronto tra la definizione di algoritmo data in precedenza e quella di programma, risulta evidente che la differenza sta nel modo in cui le istruzioni sono codificate.

Una prima distinzione può essere fatta tra:

1. linguaggi non evoluti o di basso livello (linguaggio macchina, linguaggi assemblativi);

2. linguaggi evoluti o di alto livello (algoritmici, speciali).

Ogni processore ha un proprio linguaggio, detto linguaggio macchina, che ad ogni stringa di bit fa corrispondere una operazione elementare. Questo tipo di linguaggio è molto lontano dal modo di ragionare dell'uomo. Inizialmente l’attività di codifica di algoritmi, lavoro lungo e difficile, era riservata solo a tecnici super specializzati. In seguito furono creati dei linguaggi intermedi con cui scrivere i programmi. Per l’utilizzo di un algoritmo codificato in questo modo è necessario un apposito programma traduttore che converte il programma originale (detto file sorgente) nelle corrispondenti istruzioni in linguaggio macchina (ottenendo così il file oggetto). Il primo di tali linguaggi fu il linguaggio Assembler, in cui al posto di ogni istruzione macchina viene usato un codice mnemonico ad esso associato. L'Assembler è ancora molto vicino alla logica del processore.

Successivamente sono stati ideati linguaggi non più orientati alla macchina, ma orientati alla soluzione di problemi. Con tali linguaggi, indipendenti dal processore e dalla particolare macchina, il lavoro del programmatore risulta semplificato. Le istruzioni e i dati da esse manipolati vengono rappresentati simbolicamente e viene delegato alla macchina il lavoro ripetitivo e deterministico della loro traduzione in codifiche binarie.

8.3.2. Linguaggi e automi

Per ottenere la soluzione di un problema, una volta individuata la strategia risolutiva (algoritmo), si affida la messa in atto delle operazioni che essa prevede ad un esecutore (automa).

Un automa è costruito per uno scopo determinato, ed è pertanto in grado di compiere il processo previsto per raggiungere l’obiettivo fissato, compiendo un numero finito di operazioni disposte, in reazione agli input che gli vengono forniti al momento dell’attivazione.

Ciò comporta un processo di comunicazione tra l’ideatore della strategia e il realizzatore della stessa, che è reso possibile dall’uso di opportuni linguaggi (linguaggi di programmazione).

Ciascun linguaggio di programmazione è indicato per una particolare classe di problemi, ossia per ogni campo di applicazione ci sono i linguaggi più adatti.

Un elaboratore elettronico è un automa programmabile, è possibile cioè comunicare con esso usando linguaggi diversi, ciascuno finalizzato alla soluzione di una particolare classe di problemi. Nel calcolatore sono pertanto presenti simultaneamente una grande varietà di automi, ciascuno dei quali utilizza un opportuno linguaggio.

8.3.2a Rassegna dei principali software

Il sistema operativo, che è il software di base ossia l’applicazione che controlla tutte le risorse del computer, necessita di un linguaggio il più possibile vicino al linguaggio macchina ed estremamente potente anche se complesso , ossia l’Assembler. Le parti del sistema operativo d’interfaccia con l’utente vengono generalmente scritte in C o C++.

Su un computer vengono comunemente installati programmi base di Office Automation:

· il word processor, per la realizzazione di testi scritti, che trasforma la macchina in un automa che ha sostituito le vecchie macchine da scrivere, con potenzialità assai più numerose e precise;

· il foglio di calcolo, per il calcolo di un’ampia gamma di funzioni, la realizzazione di tabelle per l’organizzazione e l’analisi di dati, la creazione di grafici descrittivi di fenomeni di varia natura (economici, statistici, fisici…);

· sistemi per la gestione di basi di dati, per la realizzazione di archivi di dati (insiemi organizzati di informazioni), la creazione di tabelle e la realizzazione di procedure per l’inserimento, la modifica e la consultazione dei dati archiviati secondo prefissati criteri;

· programmi per la realizzazione di presentazioni multimediali, utile supporto per l’attività d’insegnamento, per l’esposizione di una relazione in ambito aziendale, per la presentazione di un evento;

A questi possono essere aggiunti altri programmi secondo le specifiche esigenze:

· programmi di grafica computerizzata, per ottenere semplici disegni od anche immagini di precisione da utilizzare in ambito professionale;

· elaboratori digitali d’immagini e per la realizzazione di animazioni, con i quali è possibile ritoccare fotografie, realizzare fotomontaggi e immagini animate;

· editor di suoni, per la manipolazione e la realizzazione di file audio;

· editor di pagine web, ossia di file in formato HTML (HyperText Markup Language) pubblicabili sulla Internet, così da rendere i dati in essi contenuti consultabili direttamente con un programma di navigazione (browser).

Sono poi a disposizione per gli utenti una grande varietà di applicazioni che risolvono i più svariati problemi nell’ambito della gestione aziendale, dell’apprendimento, della ricerca scientifica.

8.3.3. Introduzione ai linguaggi di programmazione

Lo schema seguente illustra i passaggi che conducono dalla formulazione del problema alla sua soluzione.

Fig. 13 Dal problema alla sua soluzione

Il passaggio dall’algoritmo risolutore di un problema al corrispondente programma avviene mediante la codifica dell’algoritmo attraverso un linguaggio di programmazione.

I linguaggi di programmazione differiscono tra di loro per la simbologia adottata per descrivere le operazioni e per le regole sintattiche con cui si compongono le istruzioni.

Tutti i linguaggi riproducono una stessa serie di operazioni e processi effettivamente eseguibili dell’elaboratore elettronico, ossia utilizzano una stessa tipologia di istruzioni.

· Istruzioni di dichiarazione, descrivono dati e variabili utilizzati dal programma, definendone tipo e struttura. Quanto più è evoluto il linguaggio, tanto più sono semplici le istruzioni per definire strutture complesse.

· Istruzioni di assegnazione, consentono di assegnare ad una variabile un valore dello stesso tipo della variabile.

· Istruzioni di controllo, sono istruzioni che richiedono salti di sequenza nell’esecuzione del programma. Rientrano in questa categoria le istruzioni di selezione e di iterazione e i salti incondizionati.

· Istruzioni di input/output, richiedono l’ingresso di informazione da una periferica alla memoria centrale oppure l’uscita di una informazione dalla memoria centrale ad una periferica.

8.3.4. Rassegna sui Principali Linguaggi

FORTRAN (FORmula TRANslating system: sistema traduttore di formule)

Ideato nei primi anni ’50 da John Backus, dipendente IBM, per consentire a tecnici e scienziati di risolvere problemi matematici in maniera automatica, senza ricorrere ai programmatori e con l’uso di una simbologia affine a quella matematica. Ha subito successive evoluzioni ed è utilizzato attualmente in ambito matematico.

ALGOL (ALGOritmic Language: linguaggio algoritmico)

Nato alla fine degli anni ’50, è stato sviluppato da Backus e Naur per applicazioni scientifiche. Importante caratteristica innovativa è la strutturazione del programma in blocchi, delimitati da un begin iniziale e da un end finale, che sarà ripresa dalla programmazione strutturata e dal linguaggio Pascal.

LISP (LISt Processor: elaboratore di liste)

Linguaggio indirizzato alla manipolazione di espressioni simboliche e di dati strutturati ad albero, che risale alla fine degli anni ‘50. E’ applicato nella produzione di programmi traduttori, dato che le regole sintattiche di questi vengono rappresentate secondo una struttura ad albero.

COBOL (COmmon Business Oriented Language: linguaggio orientato alle applicazioni commerciali)

Ideato nel 1960 per sviluppare programmi per la soluzione di problemi aziendali nei campi dell’amministrazione e del commercio (fatturazione, contabilità, stipendi, organizzazione di dati, gestione di file,…), ha subito successive evoluzioni ed è tuttora utilizzato.

BASIC (Begginner’s All-purpose Symbolic Instruction Code: codice generale d’istruzioni simboliche per principianti)

Nato all’inizio degli anni ’60, è un linguaggio algoritmico di carattere generale non indirizzato ad alcuna applicazione specifica e di facile apprendimento ed utilizzo. La sua semplicità e versatilità ne ha determinata la rapida ed ampia diffusione e la realizzazione di successivi aggiornamenti migliorativi. Da esso discendono i linguaggi visuali orientati agli oggetti (visual BASIC), con interfaccia grafica di facile utilizzo (pulsanti, finestre,…).

PL1 (Programming Language/1: linguaggio di programmazione/1)

Ideato nel 1965 per implementare programmi appartenenti a diverse aree applicative, scientifiche e gestionali, riassume in sé le caratteristiche dei precedenti FORTRAN, ALGOL e COBOL.

LOGO (dal greco: pensiero, discorso)

Linguaggio adatto per l’apprendimento della logica della programmazione da parte dei bambini, fu ideato nel 1967. Il programmatore dispone di semplici comandi con i quali guida l’avanzamento di un cursore sullo schermo e riscontra gli effetti grafici del programma prodotto.

PASCAL (così denominato in onore del matematico francese Blaise Pascal)

Ideato da Niklus Wirth nel 1970, con l’intento di realizzare un linguaggio che facilitasse l’insegnamento della scrittura di programmi, ha trovato e trova tuttora ampia applicazione in ambito didattico. Tale linguaggio consente un alto livello di strutturazione degli algoritmi e dei dati ed offre la possibilità di definire tipi di dati diversi da quelli standard.

C (linguaggio di programmazione C)

La prima versione fu realizzata nel 1972 da Dennis Ritchie e si distingueva dai suoi predecessori per il fatto di implementare una vasta gamma di tipi di dato. E’ un linguaggio di alto livello che possiede un numero ristretto di parole chiave e di costrutti di controllo e un gran numero di operatori. Non possiede istruzioni di entrata/uscita né istruzioni per operazioni matematiche, ma questa sua apparente povertà di strumenti consente di realizzare qualsiasi programma in modo semplice. E’ stato definito “il linguaggio di più basso livello tra i linguaggi di alto livello”, perché è nato per lo sviluppo di sistemi operativi ossia software di basso livello, ma è un linguaggio potente come un linguaggio macchina e al tempo stesso di semplice utilizzo. Il sistema operativo UNIX è scritto con questo linguaggio.

C++

Nel 1983 Bjarne Stroustrup inventò C++, che, partendo dal linguaggio C del quale estende la sintassi, introduceva la programmazione Orientata agli Oggetti (Object Oriented), un modo innovativo di progettare un programma che rende il codice più semplice e riutilizzabile.

JAVA

Nato a metà degli anni ’90 ad opera della Sun Microsystem, è un linguaggio di programmazione Object Oriented utilizzabile su diverse piattaforme (Mac, PC, Unix e SGI) senza la necessità di modifiche o ricompilazioni. Si tratta di un linguaggio multipiattaforma, per il quale il compilatore non genera applicativi eseguibili dal computer, ma file che devono essere interpretati dalla JVM (Java Virtual Machine, un microprocessore virtuale) implementata sui vari sistemi. Ciò rende l’esecuzione di un’applicazione Java più lenta dei programmi normali.

Le applicazioni JAVA, eseguibili solo con la JVM, non vanno confuse con le applet Java, che sono programmi che si eseguono all’interno delle pagine web.

PHP (Hypertext Pre-Processor)

Linguaggio di scripting, si utilizza per scrivere programmi che vengono interpretati dal server su cui risiedono pagine web. Quando l’utente richiede una pagina web contenente uno script PHP, il server richiama un modulo PHP che interpreta ed esegue il codice, restituendo al server codice web semplice (HTML) che viene passato al browser dell’utente. Tale procedimento consente di costruire dinamicamente il contenuto della pagina web.

Approfondimento 1 – Aggregazione di sottosistemi

L’aggregazione di sottosistemi in un unico sistema può avvenire attraverso:

· Connessione a cascata: l’uscita di un sottosistema costituisce l’ingresso dell’altro.

Fig14 Connessione a cascata

· Connessione in parallelo: i due sottosistemi hanno lo stesso ingresso.

Fig. 15 Connessione in parallelo

· Connessione in retroazione: le uscite di uno influenzano gli ingressi dell’altro.

Fig. 16 Connessione in retroazione

Tale fenomeno di retroazione viene anche indicato col nome di feedback.

Un sistema utilizza gli input per effettuare delle azioni che comportano degli output. Una serie di azioni che concorrono al raggiungimento di un certo risultato viene chiamata processo.

Si dice processo sequenziale quando le singole azioni che lo compongono devono essere condotte in sequenza.

Gli input di un sistema avviano processi mediante i quali ottenere in uscita gli effetti a cui il sistema è stato finalizzato.

Un sistema è quindi un’entità atta ad eseguire processi per conseguire fissati obiettivi.

Possiamo distinguere:

· sistemi statici, che non si evolvono nel tempo

· sistemi dinamici, che si evolvono nel tempo

Approfondimento 2 - La Macchina di Turing.

In sostanza il concetto di automa è quello di una macchina capace di svolgere in maniera automatica, una volta sollecitata in modo opportuno, delle operazioni particolari più o meno complesse che portano a un preciso risultato.

Per le loro caratteristiche, gli automi a stati finiti sono in grado di risolvere solo quella tipologia di problemi in cui il numero di eventi da ricordare risulta essere finito e determinato a priori.

Molti matematici si sono cimentati nella ricerca di macchine computazionali astratte in grado di risolvere qualsiasi tipo di problema, o per lo meno tutti quelli risolvibili attraverso un algoritmo. Si deve a A.M. Turing nel 1936 l’identificazione formale delle caratteristiche che una macchina astratta (modello matematico) deve avere per poter rappresentare un algoritmo. Si tratta di pura astrazione matematica, ma che rappresenta un potente strumento logico-concettuale che ha posto le basi degli studi che hanno condotto alla realizzazione dei calcolatori programmabili.

La macchina di Turing è un automa composto di tre elementi:

· un nastro infinito, suddiviso in caselle, ciascuna delle quali può contenere un solo simbolo tra quelli appartenenti all’alfabeto finito d’ingresso/uscita o il carattere speciale blank;

· una testina di lettura/scrittura, con la quale l’unità di controllo legge e scrive sul nastro un simbolo per volta; parallelamente alla testina c’è un meccanismo che muove il nastro a destra o a sinistra una sola casella alla volta;

· un’unità di controllo a stati finiti.

Per simulare il funzionamento della macchina di Turing si:

1. definisce un alfabeto finito

2. sviluppano i vari stati attraverso la loro descrizione formale

3. risolve il problema mediante una tabella di transizione

La macchina ha un funzionamento ciclico: legge un simbolo dal nastro, da esso e dallo stato interno in quell’istante determina un simbolo in uscita, un nuovo stato interno e un movimento sul nastro, fino a raggiungere uno stato senza configurazione successiva, stato finale del processo.

Ad ogni operazione di un algoritmo viene associata univocamente una terna di azioni che la macchina di Turing può svolgere. Pertanto si può ipotizzare che ad ogni algoritmo corrisponde un automa risolutore, rappresentato da un’appropriata macchina di Turing.

Ogni problema risolvibile tramite un algoritmo porta alla progettazione di una specifica macchina di Turing.

Da ciò l’associazione tra problema, algoritmo risolutore del problema, macchina di Turing che calcola l’algoritmo.

Successivamente alla macchina di Turing, evidentemente legata allo specifico problema, i matematici hanno introdotto la macchina di Turing universale, la cui logica di funzionamento non è più legata all’algoritmo in esecuzione. Si tratta di una macchina programmabile in grado di memorizzare la descrizione di una qualsiasi macchina di Turing e di simularne il comportamento, in pratica una macchina di Turing capace d’interpretare un’altra macchina di Turing.

Facendo un parallelo tra teoria e realtà, la macchina di Turing è un calcolatore che svolge un solo programma, la macchina di Turing universale è un calcolatore con memorizzazione di più programmi, in grado di svolgere algoritmi diversi.

Approfondimento 3 - Categorie dei linguaggi evoluti

Sono elencate di seguito le principali categorie in cui si classificano i linguaggi di alto livello.

Linguaggi imperativi: il programma è costituito da una sequenza di istruzioni che modificano il contenuto della memoria dell'elaboratore o determinano le modalità di esecuzione di altre istruzioni; assume un ruolo fondamentale l'istruzione di assegnazione. Sono imperativi la maggior parte dei linguaggi più diffusi (Pascal, Basic, Fortran, C, Cobol, ecc.).

Linguaggi funzionali: il programma è considerato come il calcolo del valore di una funzione; in un linguaggio funzionale puro l'assegnazione esplicita è completamente assente e si utilizza solo il passaggio dei parametri. Rivestono particolare importanza la ricorsione, ossia l'utilizzo di funzioni che richiamano se stesse e, come struttura dati, la lista (sequenza ordinata di elementi). Il più importante rappresentante di questa categoria è il Lisp (LISt Processing).

Linguaggi dichiarativi: il programma è considerato come la dimostrazione della verità di una proposizione; il sorgente è costituito da una sequenza di asserzioni di fatti e regole. Non è indicato esplicitamente il flusso di esecuzione, ma dato un obiettivo di partenza (il goal) è il sistema che cerca di individuare i fatti e le regole rilevanti.

La parte dichiarativa (il cosa fare) e la parte procedurale (il come) sono nettamente separate, favorendo la leggibilità del programma.
I linguaggi logici risultano adatti a risolvere problemi che riguardano entità e le loro relazioni.

Linguaggi strutturati: la programmazione strutturata ha lo scopo di semplificare la struttura dei programmi, limitando l'uso delle strutture di controllo a pochi casi semplici. L'uso del salto incondizionato (GOTO) viene sostituito da istruzioni di controllo del flusso più strutturate (WHILE,FOR,UNTIL)

Linguaggi orientati ad oggetti:  il programma è considerato l'effetto dell'interazione di un insieme di oggetti (insiemi di dati e algoritmi che manipolano questi dati) che comunicano con l'esterno mediante messaggi. Oltre a linguaggi specializzati che implementano i principi di tale metodologia (Smalltalk), sono nate delle estensioni dei linguaggi già esistenti, che li integrano (ad es. C++ per il C, CLOS per il Lisp).

Linguaggi orientati agli eventi: in un ambiente event driven non esiste più una sequenza determinata di comandi da eseguire ma una serie di reazioni che il sistema ha rispondendo a determinati stimoli esterni o interni.

Approfondimento 4 - Le istruzioni di controllo

Di seguito con blocco intenderemo una sequenza di operazioni.

Selezione semplice

Un’istruzione di selezione semplice (istruzione condizionale) è costituita da una condizione il cui verificarsi o meno determina l’esecuzione delle operazioni di un blocco B1 oppure di un blocco B2. Lo schema può anche non prevedere una seconda alternativa.

La sintassi nei due casi è:

Fig. 17 Diagramma a blocchi della selezione semplice con e senza alternativa

Selezione multipla

L’esecuzione di uno dei blocchi alternativi B1, B2,…Bn dipende da una variabile di controllo V che può assumere uno qualunque dei valori dell’insieme {V1, V2, …Vn}. Se la variabile V non assume alcuno dei valori dell’insieme viene eseguito il blocco S.

La sintassi è:

Fig. 18 Diagramma a blocchi della selezione multipla

Iterazione enumerativa

Si fa ricorso a questa istruzione quando è noto a priori il numero N di iterazioni che l’esecutore deve svolgere. La variabile di controllo I all’ingresso del ciclo riceve il numero N e ogni volta, prima di eseguire il ciclo, si confronta il valore di I col valore finale M. Se I≤M si entra nel ciclo e I viene incrementato di un’unità. Quando il valore I supera M , il ciclo non viene eseguito e l’iterazione ha termine. Se N>M il blocco B non viene eseguito.

La sintassi è:

Fig. 19 Diagramma a blocchi dell’iterazione enumerativa

Iterazione a controllo iniziale

Un blocco di operazioni viene eseguito una o più volte mentre la condizione di controllo, posta all’inizio del ciclo, è vera. Quando la condizione è falsa si esce dal ciclo. Se la condizione di controllo è sempre falsa, il blocco P non viene mai eseguito.

La sintassi è:

Fig. 20 Diagramma a blocchi dell’iterazione a controllo iniziale

Iterazione a controllo finale

Il blocco d’istruzioni viene eseguito ripetutamente fino a quando la condizione di controllo, posta alla fine del ciclo, da falsa diventa vera. Il blocco P è eseguito almeno una volta.

La sintassi è:

Fig. 21 Diagramma a blocchi dell’iterazione a controllo finale

Indice delle Figure

Fig. 1 Analisi di un problema	pag. 6
Fig. 2 Tecnica del top-down	pag. 7
Fig. 3 Algoritmo 1 – Diagramma a blocchi	pag. 11
Fig. 4 Algoritmo 2 – Diagramma a blocchi	pag. 12
Fig. 5 Algoritmo 3 – Diagramma a blocchi	pag. 13
Fig. 6 Algoritmo 4 – Diagramma a blocchi	pag. 14
Fig. 7 Rappresentazione schematica di un sistema	pag. 19
Fig. 8 Sistema e sottosistemi	pag. 19
Fig. 9 Grafo di Moore relativo all’automa dell’esempio	pag. 22
Fig. 10 Grafo dell’orologio digitale	pag. 24
Fig. 11 Grafo dell’automa che riconosce un identificatore	pag. 24
Fig. 12 Grafo dell’automa che riconosce identificatori e numeri interi	pag. 25
Fig. 13 Dal problema alla sua soluzione	pag. 32
Fig. 14 Connessione a cascata	pag. 36
Fig. 15 Connessione in parallelo	pag. 36
Fig. 16 Connessione in retroazione	pag. 36
Fig. 17 Diagramma a blocchi della selezione semplice con e senza alternativa	pag. 41
Fig. 18 Diagramma a blocchi della selezione multipla	pag. 42
Fig. 19 Diagramma a blocchi dell’iterazione enumerativa	pag. 42
Fig. 20 Diagramma a blocchi dell’iterazione a controllo iniziale	pag. 43
Fig. 21 Diagramma a blocchi dell’iterazione a controllo finale	pag. 43
Tab. 1 Tabella di transizione relativa all’automa dell’esempio	pag. 22
Tab. 2 Matrice degli stati	pag. 23
Tab.3 Matrice delle uscite	pag. 23

BIBLIOGRAFIA

Linguaggi di programmazione

· Ballaben, Giovanna - Introduzione alla programmazione con linguaggi assemblativi / G. Ballaben - Roma - 1989

· Ausiello, Giorgio - Teoria e progetto di algoritmi fondamentali / Giorgio Ausiello, Alberto Marchetti-Spaccamela, Marco Protasi - Milano – 1990

· Baldi, Emanuele - Logo : potenza e semplicità / Emanuele Baldi e Maurizio Di Vizio - Milano – 1984

· Barrett, Dan - Javascript / Dan Barrett, Dan Livingston e Micah Brown - Milano – 2000

· Bartee, Thomas C. - Programmare in Basic / Thomas C. Bartee - Bologna – 1988

· Bellini, Alessandro - Linguaggio C / Alessandro Bellini, Andrea Guidi - Milano – 1995

· Berk, A. A. - Lisp : il linguaggio dell'intelligenza artificiale / A. A. Berk - Milano – 1988

· Biondi, Joelle - 1 : Algoritmi e linguaggi / Joelle Biondi, Gilles Clavel ; con la collaborazionedi S. Estrems ; prefazione di O. Lecarme ; edizione italiana e traduzione a cura di Alfi , Milano – 1985

· Boccato, Monica - Java : il nuovo linguaggio object oriented per le pagine WWW / Monica Boccato, Pierangelo Ferrari - Milano – 1996

· Bundy, Alan - L' automazione del ragionamento matematico : dalla dimostrazione dei teoremi alla formazione dei concetti / Alan Bundy ; edizione italiana a cura di Mauro Boscarol - Padova – 1986

· Cabodi, Gianpiero - Introduzione alla programmazione in linguaggio C : nozioni fondamentali, esempi ed esercizi / Gianpiero Cabodi, Stefano Quer, Matteo Sonza Reorda - Milano – 1995

· Casali, Aureliano - Logo / Aureliano Casali - Bologna – 1988

· Ceppatelli, Maria Grazia - Il Cobol : un linguaggio per la programmazione dei sistemi informativi aziendali / Maria Grazia Ceppatelli, Gianna Lastri - Padova – 1990

· Codonesu, Fernando - Programmare in Pascal : dalla programmazione strutturata alla programmazione orientata agli oggetti / Fernando Codonesu - Cagliari – 1993

· Crawford, Marshal A. - Cobol strutturato : corso di autoistruzione / Marshall A. Crawford, Robert T. Grauer - Milano - stampa 1989

· Crespi Reghizzi, Stefano - Compilatori interpreti : tecniche di traduzione / Stefano Crespi Reghizzi - Milano - 1990

· D'Antona, Gaetano - Linguaggio C / Gaetano D'Antona - Bologna – 1992

· Darnell, Peter A. - C : manuale di programmazione : linguaggio e tecniche di ingegnerizzazione del software / Peter A. Darnell, Philip E. Margolis - Milano – 1991

· David, Daniel Jean - Il linguaggio Ada / Daniel Jean David - Milano – 1985

· De Nicola, Rocco - Semantica operazionale e denotazionale dei linguaggi di programmazione / Rocco De Nicola, Adolfo Piperno - Torino – 1999

· Di Battista, Giuseppe - Dal linguaggio Pascal al linguaggio C / Giuseppe Di Battista, Francesco Vargiu - Milano – 1994

· Doretti, Roberto - Esercizi di Fortran / Roberto Doretti, Roberto Farabone - Milano – 1986

· Eckel, Bruce - Programmare in C++ / Bruce Eckel - Milano – 1993

· Fanelli, Biagio - Fortran, programmazione grafica ed elementi di Unix : strumenti per un laboratorio di calcolo / B. Fanelli, L. Lopez - Bari - stampa 1993

· Fasano Petroni, Margherita - Automi e linguaggi / di Margherita Fasano Petroni - Milano – 1984

· Fiorentini, Mauro - Programmare in C : standard ISO / Mauro Fiorentini, Carlo Tibaldi - Bologna – 1992

· Ghezzi, Carlo - Concetti dei linguaggi di programmazione / Carlo Ghezzi, Mehdi Jazayeri - Milano – 1989

· Ghezzi, Carlo - Informatica teorica / Carlo Ghezzi, Dino Mandrioli - Milano – 1989

· Goldberg, David Elliot - Programmare in Assembly / David E. Goldberg, Jacqueline A. Jones, Pat H. Sterbenz - Milano – 1989

· Gonnet, Gaston H. - Handbook of algorithms and data structures : in Pascal and C / G. H. Gonnet,R. Baeza-Yates - Wokingham – 1991

· Gottfried, Byron S. - Programmare in C / Byron S. Gottfried - Milano – 1992

· Gottfried, Byron S. - Programmare in Pascal / Byron S. Gottfried - Milano – 1987

· Gurewich, Nathan - Java : guida al linguaggio per creare pagine WEB interattive / Nathan Gurewich e Ori Gurewich - Milano – 1996

· Harold, Elliotte Rusty - Programmare in rete con Java / Elliotte Rusty Harold - Bresso – 1998

· Horowitz, Ellis - Fondamenti di strutture dati in C / Ellis Horowitz, Sartaj Sahni, Susan Anderson-Freed - Milano – 1993

· Hughes, Sheila - Lisp / Sheila Hughes – Milano-1987

· Jamsa, Kris - Programmare in C : segreti, scorciatoie e soluzioni / Kris Jamsa - Milano – 1991

· Koutchouk, Michel - Cobol / M. Koutchouk - Milano – 1985

· Lucas, Michel - Costruzione di algoritmi e rappresentazione dei dati : file, automi agli stati finiti / Michel Lucas, Jean-Pierre Peyrin, Pierre-Claude Scholl ; Milano – 1986

· Naughton, Patrick - Il manuale Java / Patrick Naughton - Milano – 1996

· Newcomer, Lawrence R. - Programmare in Cobol strutturato / Lawrence R. Newcomer - Milano – 1986

· Brien, Stephen K. - Turbo Pascal 7 / Stephen K. O'Brien, Steve Nameroff - Milano – 1993

· Pappas, Chris H. - Il manuale Visual C++ / Chris H. Pappas, William H. Murray, 3 - Milano – 1996

· Plauger, P.J. - Standard C library / P.J. Plauger - Milano – 1993

· Pratt, Terrence W. - Linguaggi di programmazione / Terrence W. Pratt; edizione italiana a cura di Paolo Ciancarini - Milano - c1988

· Rayward-Smith, Victor J. - Introduzione alla teoria dei linguaggi formali / V. J. Rayward-Smith ; presentazione a cura di Luigi Petrone - Torino – 1988

· Ridolfi, Pierluigi - Il nuovo Fortran : teoria, esercizi, applicazioni / Pierluigi Ridolfi - Milano -1990

· Risso, Mario - Java 2 : programmazione distribuita / Mario Risso ; Tecnes Milano - Milano – 1999

· Romani, Francesco - Appunti di teoria degli algoritmi / Francesco Romani - Genova -1989

· Rubini, Saverio - Java 1.2 senza fatica / Saverio Rubini - Milano – 1999

· Schildt, Herbert - C : Ansi C e C++ / Herbert Schildt - Milano - 1993

· Schildt, Herbert - Linguaggio C++ / Herbert Schildt - Milano – 1996

· Schildt, Herbert - Programmare in Turbo C++ / Herbert Schildt - Milano – 1991

· Schildt, Herbert - The art of C : elegant programming solutions / Herbert Schildt - Barkeley - 1991

· Schwarz, Ron - Il manuale VBScript / Ron Schwarz, Ibrahim Malluf - Milano – 1997

· Scorzoni, Fabrizia - Cobol / Fabrizia Scorzoni - Padova – 1989

· Sedgewick, Robert - Algoritmi in C++ / R. Sedgewick - Milano - 1993

· Sethi, Ravi - Linguaggi di programmazione / Ravi Sethi - Bologna – 1994

· Shammas, Namir Clement - Introduzione al C per i programmatori Turbo Pascal / Namir Shammas - Milano – 1992

· Stroustrup, Bjarne - Il linguaggio C++ / Bjarne Stroustrup - Milano– 1990

· Talo, Giuseppe - Dal Pascal al C : appunti / Giuseppe Talo ; prefazione di Cesare Mercinelli - Lecce – 1994

· Toupin, Edward B. - Programmare in C / Edward B. Toupin - Milano – 1995

· Touretzky, David S. - Common Lisp : un'introduzione graduale all'elaborazione simbolica / David S.Touretzky - Bologna – 1991

· Van der Linden, Peter - Proprio Java / Peter van der Linden - Milano – 1997

· Waldner, Flavio - Impariamo il Pascal / Flavio Waldner - Milano – 1989

· Welsh, Jim - Introduzione al Pascal / Jim Welsh, John Elder ; traduzione di Daniele Nardi, con la collaborazione di Paola Zenobi, Francesco Donini - Milano – 1989

· Wilensky, Robert - Common Lisp / Robert Wilensky - Milano -1988

· Winder, Russel - Guida al C++ : corso completo di programmazione / Russel Winder - Milano – 1993

· Zarrella, John - Traduttori di linguaggi : assemblatori, compilatori, interpreti / John Zarrella - Milano – 1987

· Zou, Luciana - Il Pascal : introduzione al linguaggio con la metodologia della programmazione strutturata / Luciana Zou - Roma - 1990

· Zou, Luciana - La programmazione in Lisp : il primo linguaggio dell'intelligenza artificiale /Luciana Zou - Roma – 1987

Automi

· Celati, Carlo - Automazione industriale : PLC, robot, intelligenza artificiale, sistemi flessibili di montaggio / Carlo Celati - Milano – 1995

· Fu, King Sun - Robotica / King-Sun Fu, Rafael C. Gonzales, C. S. George Lee - Milano – 1989

· Gini, Giuseppina - Robot : controllo, programmazione, interazione con l'ambiente / Giuseppina Gini, Maria Gini - Milano – 1983

· Isidori, Alberto - Il mondo dei robot / di Alberto Isidori - Firenze - 1986 rto Rovetta, Edmondo Turci - Milano – 1987

· Kafrissen, Edward - Industrial robots and robotics / Edward Kafrissen, Mark Stephans - Reston - c1984

· Knapp, Brian - Computer e robot / Brian Knapp - Trieste – 1996

· Hawkes, Nigel - Robot e computer / Nigel Hawkes - Brescia -1986 e - New York - c1987

· Rovetta, Alberto - Fondamenti di robotica : il rapporto uomo-macchina: aspetti scientifici, tecnologici e tecnici della robotica / Alberto Rovetta - Milano -1990

· Sciavicco, Lorenzo - Modelling and control of robot manipulators / L. Sciavicco, B. Siciliano - London - c2000

· Sciavicco, Lorenzo - Robotica industriale : modellistica e controllo di manipolatori / Lorenzo Sciavicco, Bruno Siciliano - Milano – 1995

· Scott, Peter B. - La rivoluzione robotica : automazione e trasformazione dei processi industriali/ Peter B. Scott - Padova – 1987

· Vukobratovic, Miomir - Applied dynamics of manipulation robots : modelling, analysis and examples /Miomir Vukobratovic - Berlin - c1989

home page