|
|
Teoria |
||||||
|
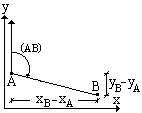
La tangente dell'angolo di direzione (AB) si ricava mediante l'espressione
|
|
||||||
|
|
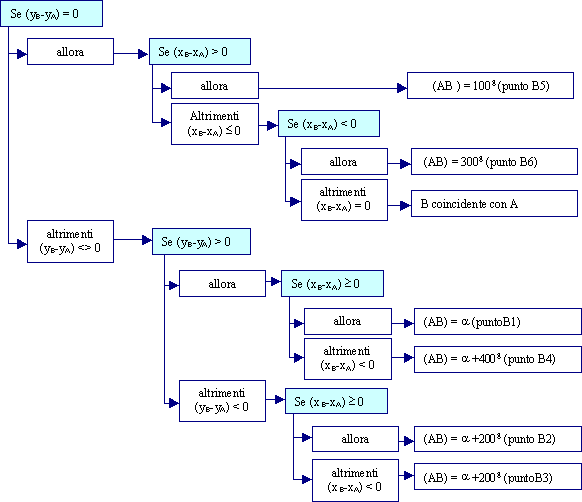
La funzione Excel ARCTAN() restituisce un angolo a nell'intervallo
con esclusione dei due estremi (punti B5 e B6 in figura). L'angolo a restituito dalla funzione è positivo se la tangente è positiva; è negativo nel caso opposto. Considerata la periodicità delle funzioni trigonometriche, ad un angolo positivo a possono corrispondere due diversi angoli di direzione (AB) collocati rispettivamente nel primo e nel terzo quadrante (punti B1 e B3 in figura). Analogamente, ad un angolo negativo a possono ricondursi due diversi valori dell'angolo di direzione (AB) collocati rispettivamente nel secondo e nel terzo quadrante (punti B2 e B4 in figura). Per stabilire il corretto valore dell'angolo (AB) a partire da a, si devono distinguere le sei diverse possibilità riportate di seguito. Ad esse bisogna aggiungere, per completezza, il caso improbabile che il punto B abbia le stesse coordinate del punto A. |
||||||
|
Punto |
(yB-yA) |
(xB-xA) |
tan (AB) |
Note |
(AB) |
||
|
B5 |
nullo |
positivo |
+¥ |
Il punto si trova sull'asse x positivo |
p / 2 |
||
|
B6 |
nullo |
negativo |
-¥ |
Il punto si trova sull'asse x negativo |
3p / 2 |
||
|
B = A |
nullo |
nullo |
Non definito |
Il punto B coincide con A |
|
||
|
B1 |
positivo |
positivo |
positivo |
Il punto si trova nel primo quadrante |
a |
||
|
B4 |
positivo |
negativo |
negativo |
Il punto si trova nel quarto quadrante |
a + 2p |
||
|
B2 |
negativo |
positivo |
negativo |
Il punto si trova nel secondo quadrante |
a + p |
||
|
B3 |
negativo |
negativo |
positivo |
Il punto si trova nel terzo quadrante |
a + p |
||