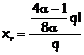Confronto
metodi di analisi. Trave a due campate uguali. Progetto IPE.
Problema. Progettare la trave continua in figura dopo aver confrontato
l’analisi elastica, l’analisi con ridistribuzione dei momenti e l’analisi plastica.
Noti: l = 4 m; q = 17,8 
; acciaio S235.
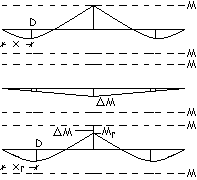
Analisi elastica.
Il momento elastico
sull’appoggio centrale vale
In campata per 
si ha
Il progetto
elastico si effettua calcolando il modulo di resistenza elastico della sezione
con la formula
Analisi con ridistribuzione dei
momenti.
Con
al tecnica della ridistribuzione dei momenti si progetta la struttura con
modalità elastica utilizzando un momento ridistribuito Mr minore di
M ed ottenendo in tal modo un profilo più piccolo:
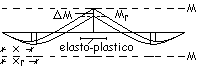
Poiché
in B il momento M è maggiore di Mr, il limite elastico viene
superato e la sezione assume un comportamento elasto-plastico al quale è
associata una quota aggiuntiva di rotazione originata dalla differenza di
momento
. Il comportamento elasto-plastico è esteso al tratto, posto
a cavallo di B, nel quale il momento risulta maggiore di Mr.
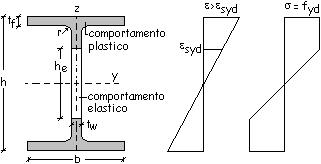
Affinché
il comportamento non diventi completamente plastico, con la conseguente formazione
di una cerniera plastica in B, il modulo di resistenza della sezione deve
essere tale da riuscire a far fronte al momento M utilizzando il calcolo
plastico
o, in altri
termini
Essendo
nella quale a è
il fattore di forma, pari a circa 1,14 per i profili IPE si ha
|
|
Tipo di sezione |
Fattore di forma |
|
|
1,14 |
|
|
|
1,27 |
|
|
|
1,50 |
|
|
|
1,70 |
|
|
|
2,00 |
|
|
|
2,37 |
|
|
Profilo IPE |
Fattore di forma |
|
80 |
1,16 |
|
|
100 |
1,15 |
|
|
120 |
1,15 |
|
|
140 |
1,14 |
|
|
160 |
1,14 |
|
|
180 |
1,14 |
|
|
200 |
1,14 |
|
|
220 |
1,13 |
|
|
240 |
1,13 |
|
|
270 |
1,13 |
|
|
300 |
1,13 |
|
|
330 |
1,13 |
|
|
360 |
1,13 |
|
|
400 |
1,13 |
|
|
450 |
1,13 |
|
|
500 |
1,14 |
|
|
550 |
1,14 |
|
|
600 |
1,14 |
|
|
Il
diagramma dei momenti dopo la ridistribuzione può essere ottenuto sommando al
diagramma elastico quello originato da DM. Contemporaneamente
alla formazione della cerniera plastica in B si ha un aumento del momento
positivo di campata con un contemporaneo avvicinamento del punto D verso
l’appoggio centrale.
La
reazione in A dopo la ridistribuzione può essere calcolata con l’equazione
La
distanza AD vale
Il momento in D
vale
|
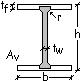
Analisi plastica.
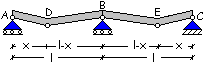
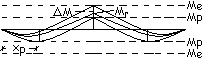
Progettando
la struttura con un momento Mp ancora più piccolo di Mr, la sezione assume un comportamento plastico con
la formazione di una cerniera plastica in B. La rotazione nel punto B aumenta
ulteriormente ed i momenti MD
ed ME crescono anch’essi.
Il
valore più piccolo che può essere assunto per Mp è quello
corrispondente ad un analogo valore per MD ed ME ; per
tale valore anche gli incastri interni in D e in E si trasformano in cerniere
plastiche e la struttura assume la forma di un meccanismo che anche un
piccolissimo ulteriore aumento del carico q porterebbe in movimento.
Raggiunto il meccanismo
le due campate AB e CD hanno lo stesso comportamento plastico di una trave con
appoggio e incastro per la quale è
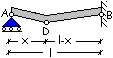
In campata per 
si ha
Per
l’equilibrio verticale del tratto AD si ha
|
|
La
reazione verticale in D è nulla perché nel punto D si ha il massimo momento
ed il taglio è nullo. |
Il
taglio nella sezione alla sinistra di B vale
Confronto tra le diverse analisi.
Riassumendo i
risultati finora ottenuti si ha
|
Caratteristica in esame |
Analisi elastica |
Analisi con ridistribuzione |
Analisi plastica |
|
MB |
|
|
|
|
xD |
|
|
|
|
MD |
|
|
|
Dal
confronto emergono dei valori più bassi delle sollecitazioni a favore
dell’analisi plastica.
Il
risparmio conseguibile è pari al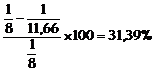 
rispetto al calcolo elastico e 
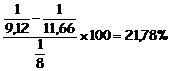rispetto al calcolo con ridistribuzione dei momenti.
|
|
In
realtà il confronto può condurre a risultati ancora più rilevanti se, oltre
alla flessione, si consideri anche il taglio. Soprattutto
in presenza di taglio trascurabile con
il metodo
plastico consente risparmi ancora più forti del metodo elastico per il quale
le Norme Tecniche non prevedono sconti. |
Tensioni di calcolo.
Le tensioni di
calcolo del materiale rispettivamente a flessione e a taglio valgono
Progetto della sezione (analisi
plastica).
Tutti
i profili della serie IPE sono di classe 1 per la quale le Norme Tecniche
consentono il calcolo plastico.
Il momento
originato dal carico q vale
Trascurando in
prima approssimazione il peso proprio incognito g1 della struttura
si ha
Il modulo di
resistenza plastico di progetto è dato da
Dal sagomario si
ricava
Wpl = 166415
mm3 ; IPE 180; g1 = 0,18 
; Av = 1125 mm2; Classe 1.
Verifica a taglio.
La resistenza di taglio
di progetto vale
Verificato
|
|
|
L’area
di taglio, per una sezione a I o ad H,
è ottenuta con l’espressione:
|
Verifica a
flessione.
Poiché
è risultato 
, le Norme Tecniche consentono di ritenere trascurabile
l’effetto del taglio: la tensione di calcolo del materiale può quindi essere
utilizzata pienamente per sopportare la flessione.
Il momento
resistente offerto dalla struttura vale
Collaudo della sezione (analisi
plastica).
Il momento a
disposizione per il carico q vale
Ad esso
corrisponde il carico variabile
Collaudo della sezione (analisi
elastica).
Dal sagomario si
ricava
Wel = 146329 mm3 ; Sy = 83208 mm3; tw
= 5,3 mm ; Iy = 13169590 mm4
La tensione di
taglio vale
Le Norme Tecniche
prevedono la verifica congiunta taglio-flessione mediante la diseguaglianza
(Von Mises)
dalla quale è
possibile ricavare
Il momento
sopportabile dalla struttura è
Il momento a
disposizione per il carico q vale
Ad esso corrisponde
il carico variabile
Confronto tra il carico limite
plastico e quello elastico.
In percentuale si
ha
|
|
La
notevole convenienza nell’adozione del metodo plastico nel calcolo agli stati
limite ultimi è in parte ridimensionata dalle maggiori richieste derivanti
dal calcolo agli stati limite di esercizio: spesso si è costretti ad
aumentare le dimensioni della sezione per limitarne le deformazioni. |
