Problema. Determinare le espressioni analitiche relative alle sollecitazioni e alle deformazioni di una trave semplicemente appoggiata con carico uniformemente distribuito.

Le reazioni vincolari della trave, considerata la simmetria del problema, valgono

Espressione analitica del taglio.

Essendo

per integrazione si ottiene

Tale espressione analitica rappresenta, com’è noto, una retta.

Per determinare il valore della costante C₁, si può porre la condizione che il taglio nella sezione A_d (cioè per x = 0) sia uguale a V_A.

L’espressione del taglio risulta, pertanto

Espressione analitica del momento flettente.

Poiché

integrando, si ottiene

Nel punto A, cioè per x = 0, si deve avere

Ciò comporta la nullità della costante C₂; il momento risulta, pertanto

espressione che geometricamente corrisponde a una parabola.

Il valore massimo del momento si verifica in corrispondenza del punto C, avente ascissa x_C, nel quale la sua derivata prima (ovvero il taglio) risulti nulla.

Il valore massimo del momento vale quindi

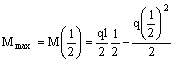
La funzione momento è crescente nel tratto AC nel quale la derivata prima, cioè il taglio, è positiva; la stessa funzione è decrescente nel tratto successivo CB caratterizzato da un taglio negativo.

Espressione analitica delle rotazioni e degli abbassamenti.

Gli abbassamenti risultano pari a

Le costanti C₃ e C₄ possono essere determinate esaminando le condizioni al contorno: gli abbassamenti dei punti A e B, all’estremità della trave, devono, infatti, risultare nulli.

Le rotazioni sono in definitiva date dalla

Le rotazioni all’estremità della trave valgono

L’equazione della linea elastica e data dalla

L’abbassamento in mezzeria vale