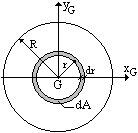
Problema. Determinare il momento di inerzia IxG di un cerchio rispetto agli assi xG e yG passanti per il baricentro G.
Momento di inerzia di un cerchio rispetto ad un asse baricentrico.
|
|
Problema. Determinare il momento di inerzia IxG di un cerchio rispetto agli assi xG e yG passanti per il baricentro G. |
I due momenti di inerzia IxG e IyG, per la simmetria del problema, risultano uguali; la loro somma è pari al momento di inerzia polare IG.
Il momento di inerzia polare IG è dato da
nella quale l’area elementare dA della corona circolare può essere calcolata come prodotto della lunghezza della circonferenza media
e dello spessore dr
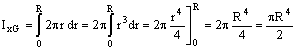
Posto D = 2 R, si ottiene
(c)
giugno 2001 Carlo PALATELLA