EC5. Esempio di calcolo a pressoflessione (h >
150 mm).
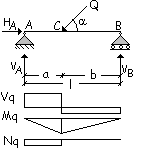
Problema. Progettare la trave in figura.
Noti: l = 3,6 m; a = 1,2 m; Q = 8 kN; a = 50°;
legno Abete/Nord S1, Classe di servizio 1, carichi variabili di lunga durata.
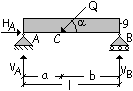
Le tensioni caratteristiche del materiale valgono
a flessione
a compressione
a taglio
Il peso specifico
medio risulta pari a 
Le
tensioni di
calcolo del materiale risultano
a flessione 
nella quale:
il coefficiente parziale di sicurezza relativo
al materiale (legno massiccio) vale 
il coefficiente
correttivo di modello per la Classe di servizio 1 e con carichi
variabili di lunga durata vale 
|
Valori di kmod |
||||||
|
Materiale |
Classe di servizio |
Classe di durata del carico |
||||
|
Permanente |
Lunga |
Media |
Breve |
Istantanea |
||
|
Legno massiccio Legno lamellare
incollato Microlamellare
(LVL) |
1 |
0,60 |
0,70 |
0,80 |
0,90 |
1,10 |
|
2 |
0,60 |
0,70 |
0,80 |
0,90 |
1,10 |
|
|
3 |
0,50 |
0,55 |
0,65 |
0,70 |
0,90 |
|
|
|
Nel
calcolo precedente si è ipotizzato
|
. In caso contrario la tensione va aumentata con la formula
. L’aumento è da effettuarsi solo per le tensioni di
calcolo a flessione e a trazione.
a
taglio
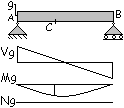
Calcolo delle sollecitazioni.
|
|
Le componenti
rispettivamente verticale ed orizzontale del carico valgono
|
Il momento di
progetto 
, trascurando in prima approssimazione il contributo del peso
proprio g (incognito), risulta
Progetto a flessione semplice.
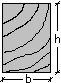
Trascurando
l’effetto della compressione, il modulo di resistenza di progetto è dato da
|
|
Trascurando
l’effetto della compressione la formula di verifica
diventa
e
quindi, in fase di progetto,
|
Imponendo il
rapporto tra le due dimensioni 
si ottiene
Assunte le
dimensioni 
il peso proprio risulta
Il modulo di
resistenza effettivo vale
Verifica a pressoflessione e taglio
|
|
Le
sollecitazioni prodotte dal peso proprio g valgono
|
A flessione si ha
A compressione si
ha
A pressoflessione
è
Verificato
|
|
Dall’analisi numerica dei valori il contributo della compressione si è rilevato di fatto trascurabile |
A taglio si
ottiene
Verificato
