EC5. Il calcolo delle deformazioni.

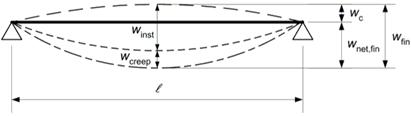
L’EC5 opera una distinzione tra le deformazioni istantanee e reversibili (w_inst) e le deformazioni differite (w_crep), irreversibili, originate da carichi permanenti a causa della viscosità (creep) e dell’umidità (Ü Classe di servizio). La deformazione netta finale (w_net,_inst) è data dalla somma della deformazione istantanea (w_inst) e della deformazione differita (w_crep) alle quali va sottratta l’eventuale deformazione impressa (w_c).

I limiti (consigliati) delle deformazioni, espressi come frazione della luce l della struttura, sono riassunti nella tabella seguente

Elemento strutturale	w_inst	w_net,fin	w_fin
Travi su due appoggi	da l/300 a l/500	da l/250 a l/350	da l/150 a l/300
Travi a sbalzo	da l/150 a l/250	da l/125 a l/175	da l/75 a l/150

In assenza di una deformazione impressa l’espressione precedente si semplifica nella

con i seguenti limiti

Elemento strutturale	w_inst	w_net,fin = w_fin
Travi su due appoggi	da l/300 a l/500	da l/150 a l/300
Travi a sbalzo	da l/150 a l/250	da l/75 a l/150

Per il calcolo delle deformazioni l’EC5 suggerisce il metodo semplificato che verrà illustrato nel seguito.

Le deformazioni istantanee.

Sono calcolate con le consuete tecniche della Scienza delle Costruzioni.

Ad esempio, gli abbassamenti in mezzeria di una trave semplicemente appoggiata assoggettata ad un carico variabile centrato valgono, rispettivamente per il peso proprio g e per il carico variabile Q

Il modulo elastico di progetto E_d fa riferimento al modulo elastico medio E_0,meansecondo l’espressione

I valori del coefficiente parziale relativo al materiale valgono

Stati limite ultimi	g_M
- combinazioni fondamentali
legno massiccio	1,30
legno lamellare incollato	1,25
pannelli di particelle o di fibre	1,30
microlamellare, compensato, pannelli di scaglie orientate	1,20
unioni	1,30
- combinazioni eccezionali	1,00

Vengono assunte per il loro intero valore le deformazioni originate dal peso proprio e dal carico variabile più importante (il carico dominante Q1); i valori per gli altri carichi variabili vengono ridotti con il coefficiente di combinazione y₀.

Categoria	y₀	y₁	y₂
Categoria A Ambienti ad uso residenziale	0,7	0,5	0,3
Categoria B Uffici	0,7	0,5	0,3
Categoria C Ambienti suscettibili di affollamento	0,7	0,7	0,6
Categoria D Ambienti ad uso commerciale	0,7	0,7	0,6
Categoria E Biblioteche, archivi, magazzini e ambienti ad uso industriale	1,O	0,9	0,8
Categoria F Rimesse e parcheggi (≤ 30 kN)	0,7	0,7	0,6
Categoria G Rimesse e parcheggi (> 30 kN)	0,7	0,5	0,3
Categoria H Coperture e sottotetti	0,0	0,0	0,0
Vento	0,6	0,2	0,0
Neve (a ≤ 1000 m)	0,5	0,2	0,0
Neve (a > 1000 m)	0,7	0,5	0,2
Variazioni termiche	0,6	0,5	0,0

Le deformazioni differite.

Le deformazioni differite sono calcolate a partire da quelle istantanee utilizzando il coefficiente di deformazione k_def ed eventualmente il coefficiente per la combinazione dei carichi y.

per il peso proprio

per il carico variabile Q₁ più importante (carico dominante)

per gli alti carichi variabili

I valori di k_def per i materiali di uso più frequente sono riportati nella tabella seguente

Valori di k_def
Materiale	Classe di servizio
	1	2	3
Legno massiccio Legno lamellare incollato Microlamellare (LVL)	0,60	0,80	2

Progetto a deformazione.

Se i limiti precedentemente indicati per le deformazioni non sono rispettati, occorre effettuare un progetto alle deformazioni aumentando le dimensioni della sezione per agire sul suo modulo di inerzia.

Ad esempio, se la deformazione istantanea w_inst calcolata con il momento di inerzia I_old supera il limite imposto w_inst,Rd la relazione che intercorre tra il precedente momento di inerzia e quello di nuovo progetto I_req è la seguente

Da essa si ricava facilmente il valore richiesto per il nuovo momento di inerzia

Le nuove dimensioni dipendono dal rapporto di progetto tra i due lati della sezione. Ad esempio, per una sezione rettangolare con

si ha