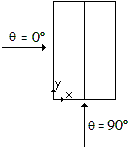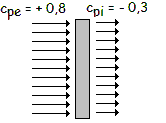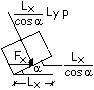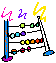EC1 Vento. Esempio di calcolo.

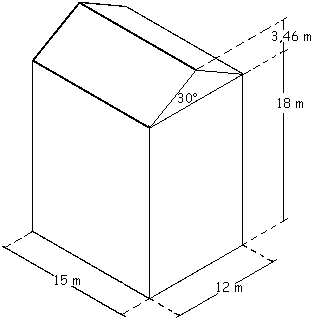
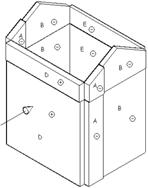
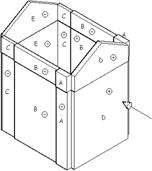
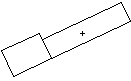
Problema. Determinare la spinta del vento sull’edificio in figura, situato a Grugliasco TO (altezza s.l.m. 293 m).

Dati progettuali:

La costruzione ha un’altezza alla linea di gronda pari a 18 m ed è collocata in un’area urbana caratterizzata da edifici di simile altezza.

La sua vita utile di progetto è pari a 50 anni (Struttura di Classe 1)

La pressione del vento p è ottenuta moltiplicando la pressione cinetica di riferimento q_b per i coefficienti di esposizione (c_e), di pressione netta (c_p) e dinamico (c_d)

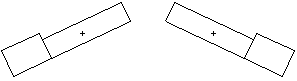
Il calcolo verrà condotto per le due direzioni del vento q = 0° e q = 90°.

Calcolo della pressione cinetica di riferimento q_b

L’edificio si trova nella zona 1 caratterizzata da Essendo l’altezza sul livello del mare pari a 293 m inferiore a a0 = 1000 m, si ha valore valido per un Periodo di Ritorno pari a 50 anni.

La pressione cinetica di riferimento vale quindi

nella quale è la densità assoluta dell’aria.

Calcolo della categoria di esposizione

L’edificio è collocato in un area urbana in un contesto di altri edifici di altezza media maggiore di 15 m: la sua classe di rugosità è, pertanto, la classe A.

La categoria di esposizione è la categoria V, corrispondente alla zona 1, con altitudine inferiore a 500 m e classe di rugosità A. A tale categoria di esposizione corrispondono zmin = 12 m z0 = 0,7 m kr = 0,23 Poiché la costruzione non è posta presso la sommità di colline o pendii isolati, il coefficiente di topografia ct è pari ad 1. L’altezza massima della costruzione è

Direzione del vento q = 0

La larghezza della parete esposta direttamente al vento vale

b = 15 m

Risulta

L’edificio verrà suddiviso in due fasce orizzontali caratterizzate da una pressione costante rispettivamente di altezza pari a b = 15 m e a .

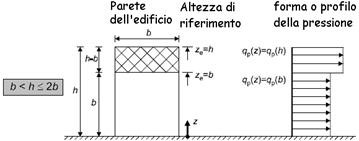
Il coefficiente di esposizione delle due fasce vale (quote superiori a z_min)

Calcolo del coefficiente dinamico c_d

Il coefficiente dinamico è assunto cautelativamente pari a 1.

Calcolo del coefficiente di pressione netta c_p

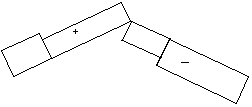
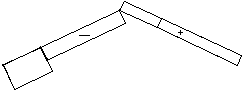
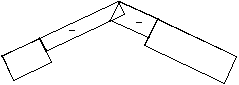
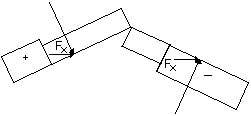
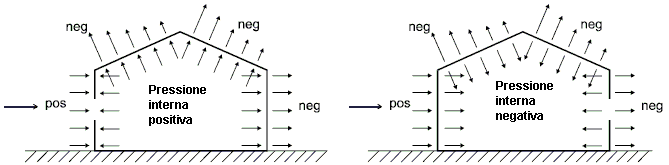
Con le convenzioni di segno rilevabili dalla figura seguente, il coefficiente di pressione netta è dato dalla differenza tra il coefficiente di pressione esterna c_pe ed il coefficiente di pressione interna c_pi, differenza effettuata considerando la condizione più sfavorevole di segno.

Il segno dei due coefficienti è positivo se il vento spinge contro la faccia della parete (pressione), negativo nel caso opposto (depressione). Nell’esempio in figura, considerando il verso delle azioni agenti sulle due facce della parete, la spinta risultante sarà data dalla loro somma. Algebricamente ciò si traduce in una differenza

Coefficiente di pressione interna c_pi

Il coefficiente di pressione esterna cpi dipende dalla quantità di aperture presenti (porte, finestre, camini, ecc … ), dalla permeabilità dell’edificio (fessure dei serramenti, ecc..) e dal rapporto tra l’altezza h e la profondità d dell’edificio.

Per edifici con permeabilità ed aperture uniformemente distribuite può assumersi il valore più oneroso tra

e

Coefficiente di pressione esterna c_pe per le pareti (direzione del vento q = 0)

Le pareti dell’edifico vengono suddivise verticalmente in zone contraddistinte dalle lettere A, B, C, D ed E.

D è l’intera parete investita dal vento;

E è l’intera parete sottovento;

A, B e C sono le zone nelle quali vengono suddivise le due pareti laterali. Il numero di divisioni dipende dal raffronto della dimensione e con la dimensione d.

La dimensione e è assunta quale valore minimo tra la larghezza b della parete investita dal vento e il doppio dell’altezza h (altezza della linea di colmo)

La profondità delle pareti laterali risulta pari a

d = 12 m

Essendo , le pareti laterali vengono suddivise nelle due sole zone A e B

Zona	Larghezza
A
B
D	15 m
E	15 m

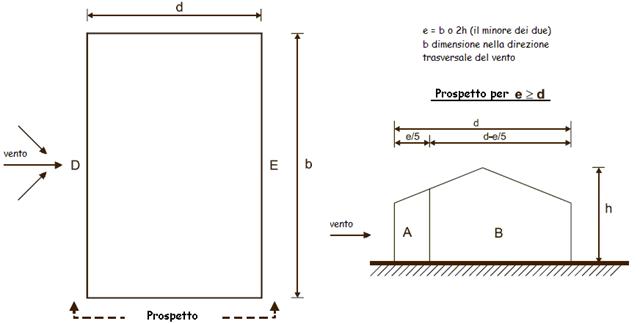
Il rapporto tra l’altezza dell’edificio (alla linea di colmo) e la sua profondità vale

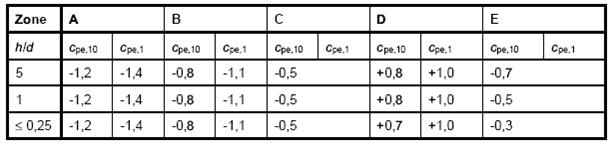
Dalla tabella 7.1 dell’EC1-2-4 si ricavano (per interpolazione) i valori del coefficiente c_pe corrispondenti al rapporto . I valori estratti dalla tabella sono riferiti ad aree investite dal vento aventi superficie minima di 10 m².

cpe per una direzione di vento Q = 0°
A	B	D	E
-1,20	-0,80	+0,80	-0,54

	per una direzione di vento Q = 0°
Zona	cpe	cpi	cp
A	-1,20	+0,2	-1,40
B	-0,80	+0,2	-1,00
D	+0,80	-0,3	1,10
E	-0,54	+0,2	-0,74

Coefficiente di pressione esterna c_pe per il tetto (direzione del vento q = 0)

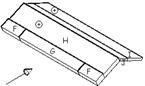
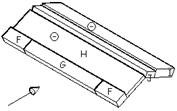
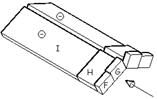
Le falde del tetto sono suddivise in aree di omogenea pressione del vento contraddistinte dalle lettere F, G, H, I, J.

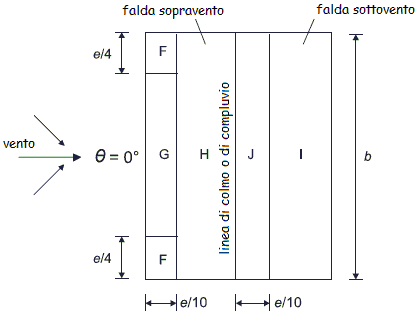
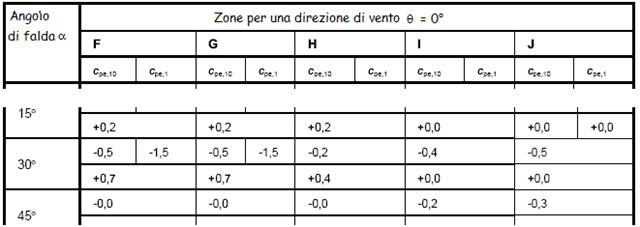
Dalla tabella 7.4 dell’EC1-2-4 si ricavano i valori del coefficiente c_pe corrispondenti all’angolo a = 30° di inclinazione delle falde del tetto. I valori riportati in seguito sono riferiti ad aree investite dal vento aventi superficie minima di 10 m².

Con una direzione del vento q = 0 la pressione può cambiare repentinamente da positiva a negativa per un angolo di falda a variabile da 5° a 45°. Sulla stessa faccia la pressione deve essere considerata tutta dello stesso segno (non è possibile cioè considerare, ad esempio un valore positivo per la zona F ed uno negativo per la zona G appartenenti alla stessa faccia). Al contrario, è necessario confrontare le quattro combinazioni di carico seguenti:

Faccia investita dal vento (sopravento)	Faccia non investita dal vento (sottovento)
positivo	positivo
positivo	negativo
negativo	positivo
negativo	negativo

cpe per una direzione di vento Q = 0° (valori negativi)					cpe per una direzione di vento Q = 0° (valori positivi)
F	G	H	I	J	F	G	H	I	J
-0,50	-0,50	-0,20	-0,40	-0,50	0,70	0,70	0,40	0,00	0,00

Zona	Dimensione nella direzione x	Dimensione nella direzione y
F
G
H		15 m
I		15 m
J		15 m

In sintesi si ha

	per una direzione di vento Q = 0° Valori positivi (pressione)
Zona	cpe	cpi	cp
F	0,7	-0,3	1,00
G	0,7	-0,3	1,00
H	0,4	-0,3	0,70
I	0	-0,3	0,30
J	0	-0,3	0,30

	per una direzione di vento Q = 0° Valori negativi(depressione)
Zona	cpe	cpi	cp
F	-0,5	0,2	-0,70
G	-0,5	0,2	-0,70
H	-0,2	0,2	-0,40
I	-0,4	0,2	-0,60
J	-0,5	0,2	-0,70

Coefficiente di pressione esterna c_pe per le pareti (direzione del vento q = 90°)

La dimensione e è assunta quale valore minimo tra la dimensione b della parete investita dal vento e il doppio dell’altezza h (altezza della linea di gronda)

La dimensione delle pareti laterali risulta pari a

d = 15 m

Essendo , le pareti laterali vengono suddivise nelle zone A, B e C

Zona	Larghezza
A
B
C
D	12 m
E	12 m

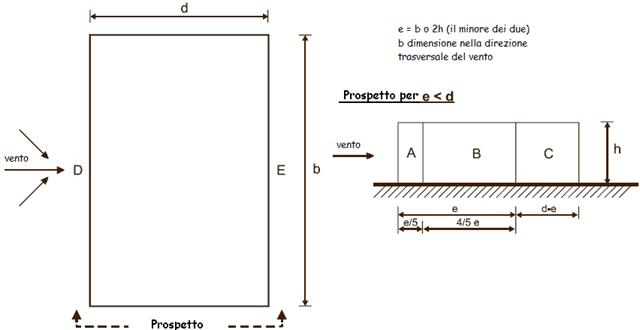
Il rapporto tra l’altezza dell’edificio (alla linea di gronda) e la sua profondità vale

Dalla tabella 7.1 dell’EC1-2-4 si ricavano (per interpolazione) i valori del coefficiente c_pe corrispondenti al rapporto . I valori estratti dalla tabella sono riferiti ad aree investite dal vento aventi superficie minima di 10 m².

cpe per una direzione di vento Q = 90°
A	B	C	D	E
-1,20	-0,80	-0,50	0,80	-0,5\

	per una direzione di vento Q =90°
Zona	cpe	cpi	cp
A	-1,20	0,20	-1,40
B	-0,80	0,20	-1,00
C	-0,50	0,20	-0,70
D	0,80	-0,30	+1,10
E	-0,51	0,20	-0,71

Coefficiente di pressione esterna c_pe per il tetto (direzione del vento q = 90°)

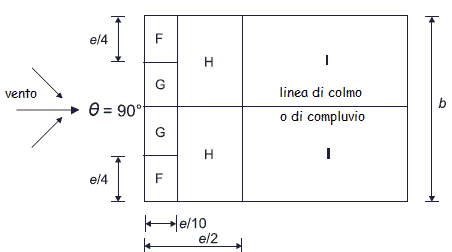
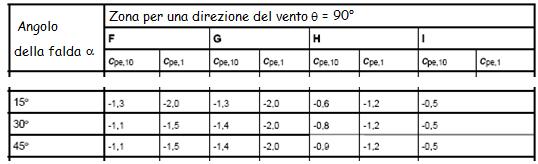
Dalla tabella 7.4 dell’EC1-2-4 si ricavano i valori del coefficiente c_pe corrispondenti all’angolo a = 30° di inclinazione delle falde del tetto. I valori riportati in seguito sono riferiti ad aree investite dal vento aventi superficie minima di 10 m².

cpe per una direzione di vento Q = 90° (valori negativi)
F	G	H	I
-1,10	-1,40	-0,80	-0,50

Per la distanza e, si assume come valore il minimo tra la dimensione b della falda investita dal vento e il doppio dell’altezza h

Zona	Dimensione nella direzione x	Dimensione nella direzione y
F
G
H	6 m
I	6 m

In sintesi si ha

	per una direzione di vento Q = 90° Valori negativi (depressione)
Zona	cpe	cpi	cp
F	-1,10	0,20	-1,30
G	-1,40	0,20	-1,60
H	-0,80	0,20	-1,00
I	-0,50	0,20	-0,70

Calcolo delle pressioni

Mentre nel progetto di una singola parete occorre prendere in considerazione il coefficiente di pressione netta cp in quello dell’intero edificio sarà utilizzato il solo coefficiente ce in quanto le pressioni interne si equilibrano reciprocamente.

In termini di pressione si ottiene

	Parete per una direzione di vento Q = 0°
Zona		ce	cd	Parete singola		Edificio
				cp		cpe
A (z ≤ 15 m)	390,63	1,63	1	-1,40	-0,89	-1,20	-0,76
A (z > 15 m)	390,63	1,89	1	-1,40	-1,03	-1,20	-0,89
B (z ≤ 15 m)	390,63	1,63	1	-1,00	-0,64	-0,80	-0,51
B (z > 15 m)	390,63	1,89	1	-1,00	-0,74	-0,80	-0,59
D (z ≤ 15 m)	390,63	1,63	1	+1,10	+0,70	+0,80	+0,51
D (z > 15 m)	390,63	1,89	1	+1,10	+0,81	+0,80	+0,59
E (z ≤ 15 m)	390,63	1,63	1	-0,74	-0,47	-0,54	-0,34
E (z > 15 m)	390,63	1,89	1	-0,74	-0,55	-0,54	-0,40

	Parete per una direzione di vento Q = 90°
Zona		ce	cd	Parete singola		Edificio
				cp		cpe
A (z ≤ 15 m)	390,63	1,63	1	-1,40	-0,89	-1,20	-0,76
A (z > 15 m)	390,63	1,89	1	-1,40	-1,03	-1,20	-0,89
B (z ≤ 15 m)	390,63	1,63	1	-1,00	-0,64	-0,80	-0,51
B (z > 15 m)	390,63	1,89	1	-1,00	-0,74	-0,80	-0,59
C (z ≤ 15 m)	390,63	1,63	1	-0,70	-0,45	-0,50	-0,32
C (z > 15 m)	390,63	1,89	1	-0,70	-0,52	-0,50	-0,37
D (z ≤ 15 m)	390,63	1,63	1	+1,10	+0,70	+0,80	+0,51
D (z > 15 m)	390,63	1,89	1	+1,10	+0,81	+0,80	+0,59
E (z ≤ 15 m)	390,63	1,63	1	-0,71	-0,45	-0,51	-0,32
E (z > 15 m)	390,63	1,89	1	-0,71	-0,52	-0,51	-0,38

	Tetto per una direzione di vento Q = 0° valori positivi (pressione)
Zona		ce	cd	Parete singola		Edificio
				cp		cpe
F	390,63	1,89	1	1,00	+0,74	+0,7	+0,52
G	390,63	1,89	1	1,00	+0,74	+0,7	+0,52
H	390,63	1,89	1	0,70	+0,52	+0,4	+0,30
I	390,63	1,89	1	0,30	+0,22	0	0,00
J	390,63	1,89	1	0,30	+0,22	0	0,00

	Tetto per una direzione di vento Q = 0° valori negativi (depressione)
Zona		ce	cd	Parete singola		Edificio
				cp		cpe
F	390,63	1,89	1	-0,70	-0,52	-0,5	-0,37
G	390,63	1,89	1	-0,70	-0,52	-0,5	-0,37
H	390,63	1,89	1	-0,40	-0,30	-0,2	-0,15
I	390,63	1,89	1	-0,60	-0,44	-0,4	-0,30
J	390,63	1,89	1	-0,70	-0,52	-0,5	-0,37

	Tetto per una direzione di vento Q = 90° valori negativi (depressione)
Zona		ce	cd	Parete singola		Edificio
				cp		cpe
F	390,63	1,89	1	-1,30	-0,96	-1,10	-0,81
G	390,63	1,89	1	-1,60	-1,18	-1,40	-1,03
H	390,63	1,89	1	-1,00	-0,74	-0,80	-0,59
I	390,63	1,89	1	-0,70	-0,52	-0,50	-0,37

	Pressioni di progetto sul tetto I valori ricavati per una direzione di vento Q = 0° sono alternativi a quelli ottenuti per una direzione di vento Q = 90°. Poiché questi ultimi sono negativi il confronto potrà essere effettuato solo con carichi di questo segno. La configurazione prevalente è quella che si verifica nella zona G per una direzione di vento Q = 90° con un carico Il carico negativo rappresenta una depressione di segno opposto a quella degli altri carichi. Esso non andrà considerata nel calcolo degli elementi strutturali in quanto tende ad alleggerirne gli effetti. Andrà, invece, attentamente preso in considerazione per l’equilibrio del manto di copertura che tende ad essere sollevato con il risultato di uno scoperchia mento del tetto. Per quanto riguarda la direzione di vento Q = 0°, per un tetto in legno, le quattro combinazioni che di solito occorre esaminare si riducono di fatto ad una sola: al contrario di un tetto in cemento armato che presenta una continuità tra le due falde, il tetto in legno presenta strutture indipendenti sulle due falde (i falsi puntoni) che devono essere valutate in maniera autonoma. Si considerano, allora, solo le configurazioni positive (quelle negative sono già state esaminate) e tra le due possibili risulta prevalente quella agente sulla falda direttamente investita dal vento, con valori delle pressioni pari rispettivamente a
	nelle zone F e G nella zona H
	Sempre per un tetto in legno, il calcolo condotto su una falda è analogo a quello sull’altra per un’evidente simmetria: una direzione di vento Q = 180° opposta alla direzione considerata Q = 0°, produce risultati invertiti sulle due falde.

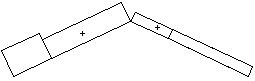
La direzione della pressione del vento è perpendicolare alle falde e risulta quindi inclinata rispetto alla verticale. Per poter essere confrontata con gli altri carichi agenti sulla struttura essa dovrà necessariamente scomposta nelle due componenti rispettivamente verticale ed orizzontale.

Calcolo delle forze

Forza agente sulla singola parete D (direzione di vento Q = 0°)

Forza orizzontale complessiva agente sull’intero edificio (direzione di vento Q = 0°)

Le forze agenti sulle due pareti laterali sono di verso opposto e si equilibrano. Verranno considerate le forze agenti sulle sole pareti D ed E oltre a quelle agenti sulla copertura.

La configurazione di carico sulla copertura prevede pressione sulla falda direttamente investita dal vento e depressione sull’altra falda: questa configurazione porta alla somma delle due componenti orizzontali Fx.

La forza agente sul tratto di falda inclinato di dimensione vale La componente orizzontale della forza F vale

Zona		Lx [m]	Ly [m]
D (z ≤ 15 m)	+0,51	15,00	15,00	114,75
D (z > 15 m)	+0,59	15,00	6,46	57,17
E (z ≤ 15 m)	-0,32	15,00	15,00	72,00
E (z > 15 m)	-0,38	15,00	6,46	36,82
F	+0,70	1,50	7,50	7,88
G	+0,70	1,50	7,50	7,88
H	+0,40	4,50	15,00	27,00
I	-0,30	1,50	15,00	6,75
J	-0,37	4,50	15,00	24,98
				355,23

Il calcolo è stato condotto per l’intero edificio. Nella pratica può risultare utile determinare le forze agenti sui singoli orizzontamenti, calcolandone, con lo stesso metodo, i valori relativi a fasce di altezza pari a quella di un singolo piano, poste a cavallo dei solai.

Effetti torsionali

Nel caso di edifici alti è consigliabile effettuare una verifica con una direzione del vento inclinata rispetto alla parete D. In questa situazione la pressione sulla parete direttamente investita dal vento può essere ipotizzata come variabile linearmente dal valore calcolato con il coefficiente c_pe fino al valore nullo.

Il valore totale della spinta del vento diminuisce ma essa presenta un’eccentricità in grado di produrre effetti torcenti sull’edificio.

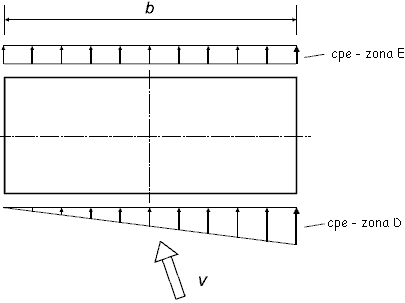
Nella tabella seguente la forza agente sulla zona D risulta dimezzata rispetto all’esempio precedente

Zona
D (z ≤ 15 m)	57,38
D (z > 15 m)	28,59
E (z ≤ 15 m)	72,00
E (z > 15 m)	36,82
F	7,88
G	7,88
H	27,00
I	6,75
J	24,98
	269,28