 NTC08. Progetto di un pilastro ad armatura minima.
NTC08. Progetto di un pilastro ad armatura minima.
Esempio di
calcolo.
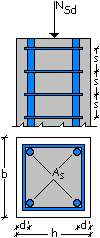
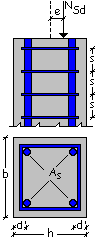
Progettare il pilastro ad armatura minima in figura
nelle seguenti ipotesi di carico:
a) carico
centrato NSd = 1600 kN;
b)
carico centrato NSd = 1600 kN e
momento MSd = 24 kNm;
c)
carico centrato NSd = 1600 kN e
momento MSd = 37,8 kNm.
Materiali
adoperati: calcestruzzo C25/30 (Rck = 30 N/mm2);
acciaio B450C.
Ambiente
di utilizzo ordinario XC1 (asciutto o permanentemente bagnato). Classe
strutturale S4 (vita nominale VN = 50 anni).
|
|
Tensioni di
calcolo. Le resistenze di calcolo per i due materiali
risultano:
Ricoprimento minimo. Per
ambiente ordinario (costruzioni con vita nominale VN = 50 anni) si ha Cmin = C25/30 ≤ C = C25/30
< C0 = C35/45 Il ricoprimento minimo per assicurare la durabilità è cmin,dur = Assunta una tolleranza di esecuzione pari a cnom = 25 + 10 = Condizione di
carico a). NSd = 1600 kN.
Progetto a
compressione semplice. La quantità minima di acciaio richiesta dalla
normativa è data da
|
|
|
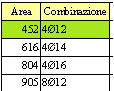
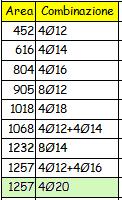
cui corrispondono in tabella 4 f 12 As = 452 mm²
Controllo del rapporto geometrico massimo di armatura: |
|
|
Fissate le dimensioni della sezione 35 ´ Ac
= 105000 mm² Controllo del rapporto geometrico minimo di armatura:
Le staffe, di diametro f 6 > f long. / 4 =
12 / 4 = s = 12 ´ 12 = L’interasse tra le armature risulta
L'eccentricità è il maggiore dei valori seguenti:
Come altezza h
è stato assunto il lato minore di Il momento di progetto risulta pari a MSd
= 1600 x 0,02 = 32,00 KNm La distanza delle armature rispetto al lembo della
sezione risulta
Lo sforzo normale ridotto vale
Il rapporto meccanico dell'armatura è dato da
|
|
|
Il rapporto meccanico dell'armatura è dato dal
rapporto tra la forza offerta dall’acciaio
e quella sopportata dal calcestruzzo
|
|
|
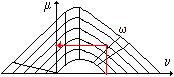
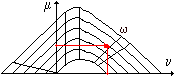
Dal diagramma di interazione si ricava m = 0,015. Il momento massimo sopportabile dalla sezione risulta
quindi
=
66666975 Nmm = 6,67 kNm < 32 kNm = MSd non
verificato. Occorre progettare nuovamente l‘armatura |
|
|
Il momento ridotto risulta pari a
Nel diagramma d’interazione la verticale condotta per n = -1,08
incrocia l’orizzontale per m = w = 0,30. |
|
|
L’armatura richiesta vale perciò
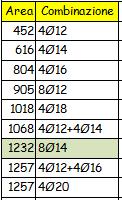
ad essi corrispondono 8 f 14 As
= 1232 mm² disposti a coppie sui quattro angoli del pilastro. Controllo del rapporto geometrico massimo di armatura:
Le staffe, di diametro f 6 > flong. / 4 =
14 / 4 = s = 12 ´ 14 = L’interasse tra le armature risulta
|
|
|
Condizione di
carico b). NSd = 1600 kN MSd = 24 kNm. E’ già
presente un’eccentricità del carico data da
L'eccentricità è il maggiore dei valori seguenti:
Il calcolo è
identico a quello sviluppato per il caso precedente. |
|
|
Condizione di
carico c). NSd = 1600 kN MSd = 37,8 kNm. E’ già
presente un’eccentricità del carico data da
L'eccentricità è il maggiore dei valori seguenti:
Il momento di progetto risulta pari a MSd
= 1600 x 0,024 = 37,8 KNm Come si è già visto, il pilastro progettato a compressione semplice è
in grado di sopportare un momento pari a MRd = 6,67 kNm < 37,8 kNm = MSd
non verificato. Occorre progettare un’armatura più grande. |
|
|
Il momento ridotto risulta pari a
Nel diagramma d’interazione la verticale condotta per n = -1,08
incrocia l’orizzontale per m = w = 0,33. |
|
|
L’armatura richiesta vale perciò
ad essi corrispondono 4Ø20 As
= 1257 mm² Controllo del rapporto geometrico massimo di armatura:
Le staffe, di diametro f 6 > flong. / 4 = 20
/ 4 = s = 12 ´ 20 = L’interasse tra le armature risulta
|