NTC08. Legno. Instabilitą. Esempio di calcolo.
Problema. Progettare il puntone in figura incernierato alle due
estremitą nelle seguenti ipotesi:
A) 
Sezione circolare
B) Sezione
quadrata
C) Sezione
rettangolare con rapporto tra i lati c = 1,4
Noti: l = 5 m; Qk = 53,2 kN; legno Abete/Nord S1,
Classe di servizio 2 (carichi variabili di media durata).
La tensione caratteristica del materiale a compressione
vale
La
tensione di
calcolo a compressione del materiale risulta
nella quale:
il coefficiente parziale di sicurezza relativo
al materiale (legno massiccio) vale 
il coefficiente
correttivo di modello per la Classe di servizio 2, con carichi
variabili di media durata vale 
|
Valori di kmod |
||||||
|
Materiale |
Classe di servizio |
Classe di durata del carico |
||||
|
Permanente |
Lunga |
Media |
Breve |
Istantanea |
||
|
Legno massiccio Legno lamellare
incollato |
1 |
0,60 |
0,70 |
0,80 |
0,90 |
1,00 |
|
2 |
0,60 |
0,70 |
0,80 |
0,90 |
1,00 |
|
|
3 |
0,50 |
0,55 |
0,65 |
0,70 |
0,90 |
|
Calcolo delle sollecitazioni.
Trascurando il peso proprio del puntone lo sforzo normale di
progetto vale
Lunghezza libera di inflessione.
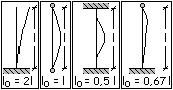
La lunghezza libera di inflessione per unasta incernierata ai due
estremi coincide con la sua altezza
A) SEZIONE CIRCOLARE
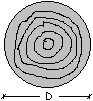
Progetto del puntone.
Dalla tabella per 
si
ricavano
e 
Larea di progetto vale
Verifica del puntone.
Il raggio di inerzia minimo risulta
La snellezza vale
Dalla tabella per 
si
ricava
Verificato
Collaudo del puntone.
B) SEZIONE QUADRATA
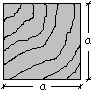
Progetto del puntone.
Dalla tabella per 
si
ricavano
e 
Larea di progetto vale
Verifica del puntone.
Il raggio di inerzia minimo risulta
La snellezza vale
Dalla tabella per 
si
ricava
Verificato
Collaudo del puntone.
C) SEZIONE RETTANGOLARE CON RAPPORTO TRA I
LATI c = 1,4
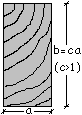
Progetto del puntone.
Dalla tabella per 
si
ricavano
e 
Larea di progetto vale
Verifica del puntone.
Il raggio di inerzia minimo risulta
La snellezza vale
Dalla tabella per 
si
ricava
Verificato
Collaudo del puntone.
©
2008 Carlo PALATELLA