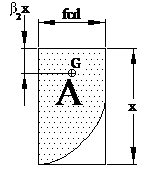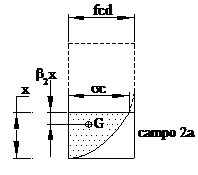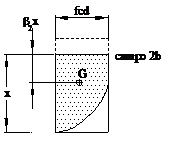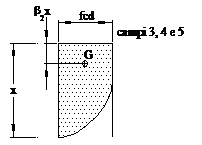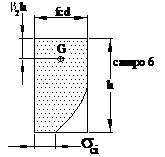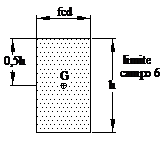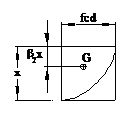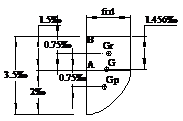NTC08. I coefficienti b1 e b2
|
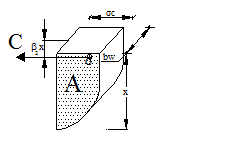
La
risultante C delle compressioni.
L'area A
del diagramma delle tensioni e la posizione del suo baricentro. |
Per la sezione
rettangolare, la risultante C delle tensioni di compressione può essere
calcolata come volume del diagramma delle tensioni, moltiplicando l'area A
per la profondità bw, larghezza della sezione. Detto b1 il rapporto tra l'area A e quella del rettangolo di lati x e
0,85fcd si ha
con b1 £ 1. Conoscendo il valore di b1 risulta
e il valore della forza C è dato da
Tale forza è
applicata nel baricentro dell'area A, ad una distanza dal bordo superiore
compresso pari a b2x, con b2 £ 0,5. I coefficienti
b1
e b2
variano con il valore di ec e possono essere tabulati per i diversi
campi. I valori massimi si presentano al limite del campo 6. In pratica si possono distinguere i seguenti casi: Ä Campo 2a (-2‰ £ ec) Ä Campo 2b (-3,5‰ £ ec < -2‰) Ä Campi 3 , 4 e 5 (ec = -3,5‰) Ä Campo 6 (-3,5‰ £ ecs < -2‰ ; -2‰ £ eci < 0 ) Ä Limite campo 6 (ec = -2 ‰) |
|
|
Campo 2a ( -2‰ £ ec) E' interessato
il solo tratto parabolico del diagramma s-e. La tensione
massima del calcestruzzo risulta sc £ fcd b1 £ 0,6667 b2 £ 0,3750. Il calcolo dei
valori di b1 e di b2 per ec = 2‰ è riportato nell'esempio 1. |
|
|
Campo 2b (-3,5‰ £ ec < -2‰) Oltre al tratto parabolico è interessato anche parte del tratto rettangolare del diagramma s-e. La tensione massima del calcestruzzo risulta sc
= fcd 0,6667 £ b1 £ 0,8095 0,3750 £ b2 £ 0,4160. |
|
|
Campi 3 , 4 e 5 (ec = -3,5‰) Il diagramma
s-e è
interessato al completo. La tensione
massima del calcestruzzo risulta sc = fcd b1 = 0,8095 b2 = 0,4160. Il calcolo dei valori di b1 e di b2 è riportato nell'esempio 2. |
|
|
Campo 6 (-3,5‰ £ ecs < -2‰
; -2‰ £ eci < 0 ) È il caso dei
pilastri in pressoflessione con debole eccentricità. La sezione è interamente
reagente e i valori sono riferiti ad h e non a x. Sono interessati una parte del tratto parabolico e l'intero tratto rettangolare del diagramma s-e. La tensione
massima del calcestruzzo risulta scs = fcd quella minima risulta sci £ fcd 0,8095 £ b1 £ 1 0,4160 £ b2 £ 0,5 |
|
|
Limite campo 6 (ec = -2‰) È il caso della
compressione semplice. La sezione è interamente reagente e i valori sono
riferiti ad h e non a x. Il diagramma
delle tensioni è costante con sc =
fcd Risulta b1 = 1 e b2 = 0,5 valori massimi dei due coefficienti. |
I coefficienti b1 e b2. Esempi di calcolo.
|
Il segmento
parabolico.
Il diagramma
delle tensioni per ec = -2‰. |
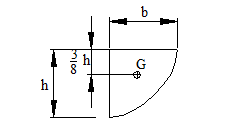
Esempio. Campo 2. Calcolare i
coefficienti b1 e b2 nel campo 2 con una deformazione ec = -2‰. Il diagramma delle tensioni comprende per intero il tratto parabolico del diagramma s-e. L'area del segmento parabolico è data dall'espressione
Nel caso in esame si ha
Il baricentro del segmento parabolico è posizionato ad una distanza
Nel caso in esame si ha 0,375x
|
|
|
Esempio. Limite campi 3-4. Calcolare i
coefficienti b1 e b2 al limite nei campi 3 e 4 (ec = -3.5‰). Il diagramma delle tensioni comprende l'intero diagramma s-e. L'area della parte parabolica del diagramma risulta
L'area della parte rettangolare del diagramma vale
L'area dell'intero diagramma è data da
Il coefficiente b1 vale
Per calcolare la
posizione del baricentro G si applica il teorema di Varignon. Il baricentro
del segmento parabolico Gp dista da A
Il baricentro del rettangolo Gr dista da B
Per Varignon si ha
|
