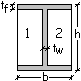
IPE Caratteristiche geometriche.
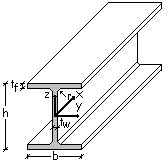
Gli assi di riferimento e la
notazione.
Secondo le Norme
Tecniche gli
assi di riferimento risultano orientati rispettivamente:
asse x nel senso della luce della trave
asse y orizzontale
asse z verticale
Tale orientamento risulta compatibile con la
maggior parte dei programmi di calcolo.
Per quanto
riguarda la notazione, gli spessori sono identificati con il simbolo t (thickness) e con il pedice rispettivamente f (flange) per l’ala e w (web) per l’anima.
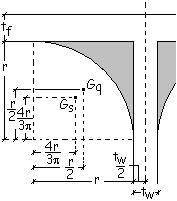
I raccordi.
Considerando un
settore circolare di raggio r, la posizione del suo baricentro è evidenziata
nella figura seguente
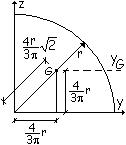
Il suo momento di
inerzia rispetto all’asse y è pari ad un quarto di quello dell’intero cerchio
rispetto allo stesso asse
Applicando il
teorema di Huygens, il momento di inerzia del settore rispetto al suo
baricentro vale
Il raccordo verrà
visto come differenza tra un quadrato di lato pari al raggio ed il settore
circolare.
La sua area vale
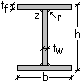
L’area del profilo.
L’area del profilo
può essere ottenuta sommando all’area delle due basi quella dell’anima e dei
quattro raccordi
Il momento di inerzia Iy
rispetto all’asse baricentrico y.
Il
momento di inerzia Iy può essere ottenuto considerando la sezione
composta dal rettangolo di dimensioni b e h al quale si sottrae l’area dei due
rettangoli 1 e 2 ed, infine dai quattro raccordi considerati singolarmente,
come si è già detto, quale differenza tra un quadrato ed un settore circolare.
La distanza del
baricentro del quadrato rispetto all’asse y vale
La distanza del
baricentro del quadrato rispetto all’asse y vale
Si ha quindi
Il momento di inerzia Iz
rispetto all’asse baricentrico z.
Il
momento di inerzia Iz può essere ottenuto considerando la sezione
composta dalle due ali, dall’anima centrale e dai quattro raccordi considerati
singolarmente, come si è già detto, quale differenza tra un quadrato ed un
settore circolare.
La distanza del
baricentro del quadrato rispetto all’asse z vale
La distanza del
baricentro del quadrato rispetto all’asse z vale
Si ha quindi
Il modulo di resistenza plastico
Wpl.y rispetto all’asse baricentrico y.
Poiché
la sezione è simmetrica, il modulo di resistenza plastico può essere calcolato
moltiplicando per due il momento statico di metà sezione rispetto agli assi di
simmetria.
Il modulo di resistenza plastico
Wpl.z rispetto all’asse baricentrico z.
Poiché
la sezione è simmetrica, il modulo di resistenza plastico può essere calcolato
moltiplicando per due il momento statico di metà sezione rispetto agli assi di
simmetria.
Caratteristiche geometriche
derivate.
|
|
y |
z |
|
raggio di inerzia |
|
|
|
modulo di resistenza elastico |
|
|
|
momento statico di metà sezione rispetto
all’asse baricentrico |
|
|
|
|
Il
momento statico di metà sezione rispetto all’asse baricentrico può essere
utilizzato per determinare il valore esatto della tensione massima di taglio
secondo l’espressione di Jouravski |
Il modulo di resistenza
elasto-plastico Wel.pl.y rispetto all’asse baricentrico y.
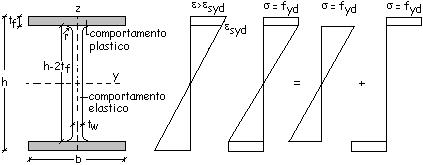
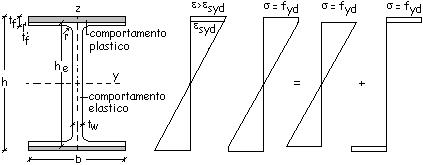
Se
la deformazione massima a flessione e supera la deformazione esyd, corrispondente alla tensione di
snervamento fyd, la sezione ha un comportamento elastico nella sua
parte centrale di dimensione pari ad he ed un comportamento plastico
nelle due parti rispettivamente superiore ed inferiore.
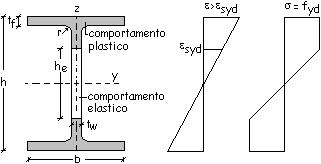
Quando
la deformazione massima e supera notevolmente la deformazione esyd, he tende a zero: la sezione ha
un comportamento totalmente plastico e ad essa corrisponde il modulo di
resistenza plastico Wpl.y calcolato precedentemente.
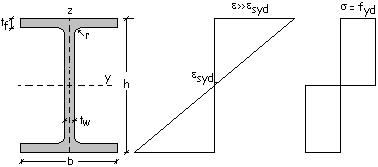
La
relazione esistente tra la deformazione massima e e l’altezza he
può essere determinata scrivendo una relazione di similitudine tra triangoli.
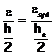
a) Zona elastica
che interessa l’anima (al di sotto del raccordo)
Il calcolo del
modulo elasto-plastico Wel.pl.y può essere condotto con la modalità
seguente:
al modulo plastico
si sottrae la quota (di tipo plastico) relativa alla zona elastica di altezza
pari ad he e si aggiunge la quota Wel (di tipo elastico)
relativa alla medesima altezza
Si ha quindi:
|
|
La
formula appena ricavata, con una piccola approssimazione, può essere
adoperata anche nel caso che la zona elastica interessi i raccordi ala-anima. |
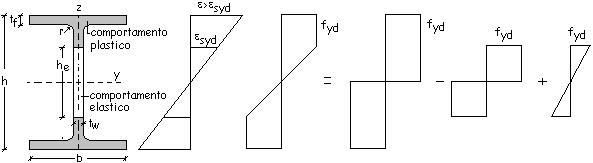
b) Zona elastica
che interessa l’ala
Il calcolo del
modulo elasto-plastico Wel.pl.y può essere effettuato con la
modalità seguente:
si determina il momento di inerzia Iey e quindi il modulo di
resistenza elastico We el.y del profilo di altezza he e
spessore dell’ala 
si aggiunge la quota di modulo plastico
delle due ali di altezza pari a 
Si ha
|
|
All’attacco
ala-anima si ha
t’f
= 0
|
