

Facendo seguito alla costruzione di una curva di Bézier, il passo importante successivo consiste nel trovare il punto C(u) sulla curva per un particolare u. Un modo semplice è quello di assegnare un valore a u in ogni funzione di base, calcolare il prodotto di ciascuna funzione di base e del suo corrispondente punto di controllo e infine sommare i termini. Pur essendo questa procedura corretta, tuttavia non è numericamente stabile (vale a dire potrebbe introdurre errori numerici durante le operazioni necessarie per calcolare i polinomi di Bernstein).
Nel seguito per semplicità di notazione indicheremo solamente i numeri relativi ai punti di controllo, vale a dire i punti di controllo saranno 00 per P0, 01 per P1, ..., 0i per Pi, ..., 0n per Pn. Gli 0 in questi numeri indicano l'iterazione iniziale o di ordine 0. In seguito questa sarà indicata con 1, 2, 3 e così via.
Il concetto fondamentale dell'algoritmo di de Casteljau's è scegliere un punto C nel segmento di linea AB tale che C divide il segmento di linea AB in un rapporto di u:1-u (vale a dire il rapporto della distanza tra A e C e quella tra A e B è u). Troviamo un modo per determinare il punto C.

Il vettore da A a B è B - A. Poiché u è un rapporto compreso tra 0 e 1, il punto C è situato nella posizione u(B - A). Considerando la posizione di A, il punto C sarà A + u(B - A) = (1 - u)A + uB. Pertanto, dato u, (1 - u)A + uB è il punto C tra A e B che divide AB nel rapporto u:1-u.
L'idea dell'algoritmo di de Casteljau è la seguente. Supponiamo di voler trovare C(u), dove u si trova nell'intervallo [0,1]. Cominciando con la prima polilinea, 00-01-02-03...-0n, utilizziamo la formula sopra per trovare un punto 1i sulla gamba (vale a dire sul segmento di linea) da 0i a 0(i+1) che divide il segmento di linea 0i e 0(i+1) nel rapporto u:1-u. In tal modo otterremo n punti 10, 11, 12, ...., 1(n-1). Essi definiranno una nuova polilinea di n- 1 gambe.

Nella figura sopra u è 0.4. 10 è nella gamba di 00 e 01, 11 è nella gamba di 01 e 02, ..., e 14 è nella gamba di 04 e 05. Tutti questi nuovi punti sono rappresentati nel colore blu.
I nuovi punti sono indicati come 1i. Se ora applichiamo la procedura a questa nuova polilinea, otterremo una seconda polilinea di n - 1 punti 20, 21, ..., 2(n-2) e n - 2 gambe. Partendo da questa polilinea, possiamo costruirne una terza di n - 2 punti 30, 31, ..., 3(n-3) e n - 3 gambe. Ripetendo la procedura n volte otterremo il singolo punto n0. De Casteljau ha dimostrato che questo è il punto C(u) sulla curva che corrisponde a u.
Continuiamo con la figura sopra. Sia 20 il punto nella gamba di 10 e 11 che divide il segmento di linea 10 e 11 nel rapporto of u:1-u. Analogamente scegliamo 21 sulla gamba di 11 e 12, 22 sulla gamba di 12 e 13, e 23 sulla gamba di 13 e 14. Questo fornisce una terza polilinea definita da 20, 21, 22 e 23. Questa terza polilinea ha 4 punti e 3 gambe. Continuando a procedere in questo modo si ottiene una nuova polilinea di tre punti 30, 31 e 32. Da questa quarta polilinea ne ricaviamo una quinta di due punti 40 e 41. Procedendo un'ultima volta otteniamo 50, vale a dire il punto C(0.4) sulla curva.
Questa è l'interpretazione geometrica dell'algoritmo di de Casteljau's, uno dei risultati più eleganti nel disegno di curve.

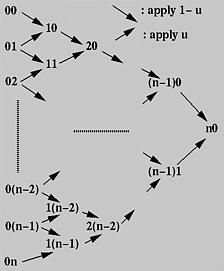
Innanzitutto tutti i punti di controllo sono disposti in una colonna, quella più a sinistra nella figura. Per ogni coppia di punti adiacenti di controllo tracciamo una freccia in direzione sud-est ed una in direzione nord-est e scriviamo un nuovo punto nell'intersezione delle due frecce. Ad esempio, se i due punti adiacenti sono ij e i(j+1), il nuovo punto sarà (i+1)j. La freccia in direzione sud-est (rispettivamente nord-est) significa moltiplicare per 1 - u (rispettivamente u) il punto all'origine della freccia ij (rispettivamente i(j+1)), e il nuovo punto ne è la somma.
Pertanto dalla colonna iniziale 0 calcoliamo la colonna 1; dalla colonna 1 otteniamo la colonna 2 e così via. Alla fine dopo n applicazioni giungiamo ad un singolo punto n0 e questo è il punto sulla curva. L'algoritmo seguente riassume quello che abbiamo discusso. Esso prende un array P di n+1 punti e una u compresa tra 0 e 1, e fornisce un punto sulla curva di Bézier C(u).


Più precisamente, l'elemento Pi,j è la somma di of (1-u)Pi-1,j (angolo in alto a sinistra) e uPi-1,j+1 (angolo in basso a destra). Il risultato finale (vale a dire il punto sulla curva) è Pn,0. Basandosi su quest'idea, è possibile giungere alla seguente procedura ricorsiva:
Questa procedura è semplice e breve, tuttavia risulta estremamente inefficiente. Ecco il motivo. Cominciamo con una chiamata a deCasteljau(n,0) per il calcolo di Pn,0. L'istruzione else divide questa chiamata in altre due chiamate, deCasteljau(n-1,0) per il calcolo di Pn-1,0 e deCasteljau(n-1,1) per il calcolo di Pn-1,1.
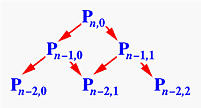
Consideriamo la chiamata a deCasteljau(n-1,0). Essa si divide in altre due chiamate, deCasteljau(n-2,0) per il calcolo di Pn-2,0 e deCasteljau(n-2,1) per il calcolo di Pn-2,1. La chiamata a deCasteljau(n-1,1) si divide in due chiamate, deCasteljau(n-2,1) per calcolare Pn-2,1 e deCasteljau(n-2,2) per calcolare Pn-2,2. Pertanto deCasteljau(n-2,1) è richiamata due volte. Se continuassimo ad espandere le chiamate alla funzione scopriremmo che quasi tutte le chiamate alla funzione per il calcolo di Pi,j vengono ripetute, non una ma molte volte. Quanto è ridondante la procedura? Di fatto lo schema è identico a quello usato per il calcolo dell'n-mo numero di Fibonacci:

Lo schema triangolare di calcolo dell'algoritmo di de Casteljau offre un'osservazione interessante. Osserviamo il calcolo seguente di una curva di Bézier di grado 7 definita su 8 punti di controllo 00, 01, ..., 07. Consideriamo un insieme di punti consecutivi sulla stessa colonna dei punti di controllo di una curva di Bézier. Allora, assegnata una u nell'intervallo [0,1], come calcoliamo il punto corrispondente su questa curva di Bézier? Se l'algoritmo di de Casteljau viene applicato a questi punti di controllo, il punto sulla curva è il vertice opposto alla base del triangolo equilatero formato dai punti scelti!

Per esempio, se i punti scelti sono 02, 03, 04 e 05, il punto sulla curva definito da questi quattro punti di controllo che corrisponde a u è 32. Osservare il triangolo blu. Se i punti scelti sono 11, 12 e 13, il punto sulla curva è 31. Vedere il triangolo giallo. Se i punti scelti sono 30, 31, 32, 33 e 34, il punto sulla curva è 70.
Per la stessa ragione, 70 è il punto sulla curva di Bézier definita dai punti di controllo 60 e 61. Esso è anche il punto sulla curva definita da 50, 51 e 52, e sulla curva definita da 40, 41, 42 and 43. In generale, se scegliamo un punto e disegniamo un triangolo equilatero come mostrato sopra, la base del triangolo equilatero consiste dei punti di controllo a partire dai quali si calcola il punto scelto..