
Il significato di suddivisione di una curva è tagliare una assegnata curva di Bézier in C(u) per qualche u in due segmenti di curva, ciascuno dei quali è ancora una curva di Bézier. Poiché le curve di Bézier risultanti devono avere i rispettivi nuovi punti di controllo, l'insieme originale di punti di controllo non è più necessario. Inoltre, poiché la curva originaria di Bézier di grado n viene divisa in due parti, ciascuna delle quali è un sottoinsieme della curva originaria di Bézier di grado n, le curve di Bézier risultanti devono avere grado n.
Il problema è il seguente:
Assegnato un insieme di n + 1 punti di controllo P0, P1, P2, ..., Pn ed il valore del parametro u compreso tra 0 e 1, vogliamo trovare due insiemi di n+1 punti di controllo Q0, Q1, Q2, ..., Qn e R0, R1, R2, ..., Rn tali che la curva di Bézier definita dai Qi (rispettivamente dai Ri) è la parte della curva originaria di Bézier su [0,u] (rispettivamente su [u,1]).
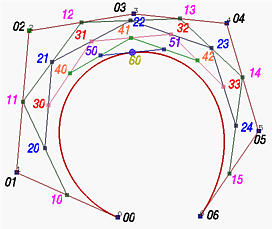
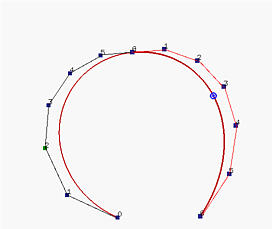
Se da una lato una dimostrazione rigorosa risulta alquanto tediosa, l'algoritmo è invece semplicissimo. Infatti, l'algoritmo di de Casteljau per calcolare il punto C(u) sulla curva fornisce tutte le informazioni necessarie. Nella figura sotto a sinistra sono mostrati tutti i passi intermedi dell'algoritmo di de Casteljau per calcolare C(u); a destra sono mostrate le suddivisioni della curva in C(u) insieme alle corrispondenti polilinee di controllo.


Se confrontiamo attentamente le due figure, notiamo che la polilinea di sinistra consiste dei punti P00 = P0, P10, P20, P30, P40, P50 e P60 = C(u), mentre la polilinea di destra consiste dei punti P60 = C(u), P51, P42, P33, P24, P15 e P06 = P6. Le fugure seguenti illustrano la scelta di questi punti.


Ricordiamo dallo schema del calcolo triangolare dell'algoritmo di de Casteljau che assegnato u occorrono n iterazioni per calcolare C(u). Nel corso del calcolo è possibile raccogliere il primo ed ultimo punto di ciascuna colonna; alla fine raccogliendo tutti i primi (rispettivamente ultimi) punti si ottiene la suddivisione che corrisponde alla parte della curva originaria definita su [0,u] (rispettivamente su [u,1]). Pertanto nello schema triangolare il bordo superiore in direzione delle frecce e quello inferiore nella direzione opposta delle frecce forniscono i punti di controllo rispettivamente del primo e secondo segmento di curva.

Notare che poiché il segmento di linea definito da 50 e 51 risulta tangente alla curva nel punto 60, l'ultima gamba della curva di sinistra (vale a dire dal punto 50 al punto 60) è tangente alla curva di sinistra, mentre la prima gamba della curva di destra (cioè dal punto 60 al punto 51) è tangente alla curva di destra.

La suddivisione della curva ha diverse applicazioni. Per esempio è utile per calcolare l'intersezione di due curve di Bézier, per il rendering delle curve di Bézier e per rendere più semplice il disegno della curva. Supponiamo di aver disegnato una curva ma di non essere soddisfatti del risultato. Possiamo allora voler suddividere la curva in due parti in un punto appropriato, una soddisfacente e l'altra no. Possiamo quindi dimenticarci quella soddisfacente e concentrarci su quella non soddisfacente.
Possimao applicare la suddivisione quante volte vogliamo. Tuttavia va tenuto presente che se vogliamo che i segmenti di curva suddivisi si uniscano in modo dolce dobbiamo mantenere il punto di unione ed i due punti adiacenti collineari.