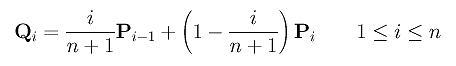

Molte applicazioni che vedono coinvolte due o più curve di Bézier richiedono che tutte le curve abbiano lo stesso grado. Inoltre anche se curve di Bézier di grado più elevato richiedono un maggiore tempo di calcolo, tuttavia esser risultano maggiormente flessibili nel disegnare forme. Pertanto risulta molto utile aumentare il grado di una curva di Bézier senza variarne la forma. Notare che "senza variare la forma della curva" è il punto fondamentale, perché altrimenti non ha alcun senso pratico semplicemente aumentare il grado della curva di Bézier. Elevare il grado di una curva di Bézier senza variarne la forma viene denominato elevazione del grado. Nel seguito discuteremo solamente un algoritmo.
Supponiamo di avere una curva di Bézier di grado n definita per mezzo di n + 1 punti di controllo P0, P1, P2, ..., Pn e che vogliamo elevarne il grado a n + 1 senza variarne la forma. Poiché una curva di Bézier di grado n + 1 è definita mediante n + 2 punti di controllo, é necessario trovare tale insieme di punti di controllo. Ovviamente P0 and Pn devono appartenere al nuovo insieme perché la nuova curva vi deve passare. Pertanto dobbiamo individuare solo n nuovi punti di controllo. Siano Q0, Q1, Q2, ..., Qn+1 i nuovi punti di controllo. Come detto in precedenza Q0 = P0 and Qn+1 = Pn. Gli altri punti di controllo sono calcolati come segue:
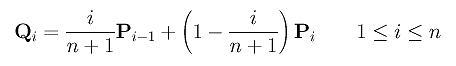
Scritte per ogni punto di controllo da Q1 to Qn le equazioni si esprimono come
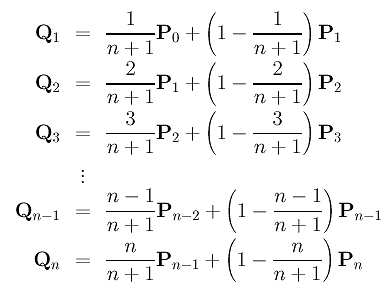
Ogni gamba della polilionea originale contiene esattamente un nuovo punto di controllo. Pioù precisamente, la gamba Pi-1Pi contiene il nuovo punto di controllo Qi. Ricordiamo dalla discussione sull'algoritmo di de Casteljau che un punto C su un segmento di linea AB che divide AB nel rapporto 1-u può essere scritto come C = (1 - u)A + uB. Dalle formule per i nuovi punti di controllo osserviamo che Qi divide il segmento Pi-1Pi nel rapporto 1 - i/(n+1):i/(n+1). Tuttavia contrariamente all'algoritmo di de Casteljau tale rapporto non è costante ma dipende da i. Tuttavia il calcolo è molto simile a quello dell'algoritmo di de Casteljau.
Una volta ottenuto il nuovo insieme di punti di controllo, l'insieme originario non è più necessario. Poiché ogni gamba della polilinea di controllo originaria contiene un nuovo punto di controllo, la procedura di sostituzione del vecchio insieme con quello nuovo può essere interpretata come un'eliminazione degli angoli dei punti di controllo originari. La figura seguente illustra l'effetto di rimozione degli angoli. Essa mostra una curva di Bézier di grado 4 i cui punti di controllo sono indicati con rettangoli rossi e la polilinea mediante una linea tratteggiata blu. Dopo aver elevato il grado a 5, la nuova polilinea di controllo e' mostrata a tratto continuo. Risulta evidente che tutti gli angoli sono stati eliminati. La tabella a sinistra fornisce il rapporto su ogni gamba della polilinea originale di controllo.
|

|
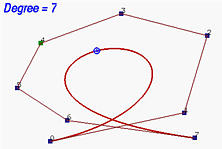
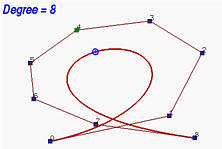
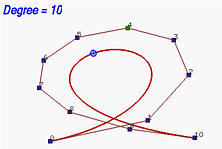
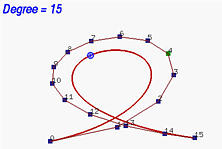
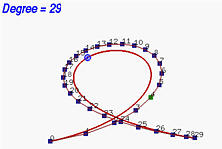
Notare che l'elevazione del grado può essere applicata a ripetizione. Notare anche che l'elevazione del grado aumenta il numero di punti di controllo. Inoltre la nuova polilinea di controllo si sposta verso la curva. Nelle figure seguenti si parte da una curva di Bézier di grado 6 con 7 punti di controllo; si eleva poi il grado a 7, 8 10, 15 e 29. Si osserva che la forma della curva non cambia con l'elevazione del grado e che la polilinea di controllo si sposta più vicino alla curva. Al limite, quando il grado tende ad infinito la polilinea di controllo si avvicina alla curva che ne risulta la posizione limite.