Derivate di una curva di Bézier

Per calcolare vettori tangenti e normali ad una curva di Bézier in un punto dobbiamo calcolare le derivate prima e seconda in quel punto. Fortunatamente il calcolo delle derivate di una curva di Bézier in un punto è semplice.

Ricordiamo che la curva di Bézier definita per mezzo degli n + 1 punti di controllo P₀, P₁, ..., P_n è rappresentata dalla seguente equazione:

dove B_n,i(u) è definito come

Poiché i punti di controllo sono costanti e indipendenti dalla variabile u, il calcolo della curva della derivata C'(u) si riconduce al calcolo delle derivate dei B_n,i(u). Dopo qualche semplice manipolazione algebrica abbiamo il seguente risultato per B^'_n,i(u):

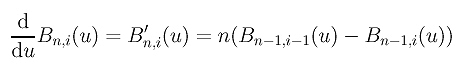
Quindi calcolando la derivata della curva C(u) si ottiene:

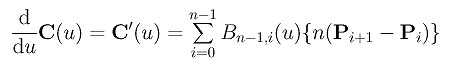
Siano Q₀ = n(P₁ - P₀), Q₁ = n(P₂ - P₁), Q₂ = n(P₃ - P₂), ..., Q_n-1 = n(P_n - P_n-1). L'equazione sopra si riduce alla seguente:

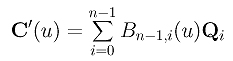
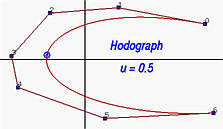
Pertanto la derivata di C(u) è una curva di Bézier di grado n - 1 definita per mezzo dei punti di controllo n(P₁ - P₀), n(P₂ - P₁), n(P₃ - P₂), ..., n(P_n - P_n-1). Questa curva viene solitamente chiamata come l'odografo della curva originaria di Bézier. Notare che P_i+1 - P_i è il vettore direzione da P_i a P_i+1 e n (P_i+1 - P_i) è n volte più lungo del vettore direzione. Una volta noti i punti del poligono di controllo, i punti di controllo delle derivate si ottengono immediatamente. La figura di sinistra mostra una curva di Bézier di grado 7 e la figura di destra mostra la sua derivata che è una curva di Bézier di grado 6.

Le curve di Bézier sono tangenti alla loro prima e ultima gamba

Unione di due curve di Bézier con continuità C¹

Il fatto che una curva di Bézier sia tangente alla prima e ultima gamba ci fornisce una tecnica per unire due o più curve di Bézier per disegnare una forma desiderata. Sia C(u) la prima curva definita dagli m + 1 punti di controllo P₀, P₁, P₂, ..., P_m. Sia D(u) la seconda curva definita dagli n + 1 punti di controllo Q₀, Q₁, Q₂, ..., Q_n. Se vogliamo unire assieme le due curve di Bèzier allora P_m deve essere uguale a Q₀. Ciò garantisce un'unione continua di classe C⁰. Ricordiamo che la prima curva è tangente all'ultima gamba e la seconda curva è tangente alla prima gamba. Di conseguenza per ottenere una transizione liscia, P_m-1, P_m = Q₀, e Q₁ deve giacere sulla stessa linea in modo che la direzione da P_m-1 a P_m e la direzione da Q₀ a Q₁ sono uguali. Questo e' mostrato nella figura sotto.

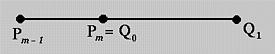
Se l'unione delle due curve di Bézier così ottenuta appare liscia, tuttavia risulta ancora un'unione di classe C⁰ e non ancora di classe C¹. Tuttavia è di classe G¹, perché hanno le stesse direzioni del vettore tangente. Per raggiungere la continuità di classe C¹ dobbiamo essere certi che il vettore tangente in u = 1 della prima curva, C'(1), e il vettore tangente in u = 0 della seconda curva, D'(0), are identici. In altre parole vale la seguente equazione:

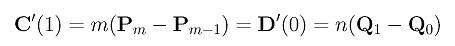
Tale relazione stabilisce che per raggiungere la continuità di classe C¹ nel punto di unione il rapporto della lunghezza dell'ultima gamba della prima curva (cioè |p_m - p_m-1|) e la lunghezza della prima gamba della seconda curva (cioè |q₁ - q₀|) deve essere n/m. Poiché i gradi m e n sono fissi, possiamo regolare le posizioni di p_m-1 or q₁ sulla stessa linea in modo che la relazione sopra sia soddisfatta.

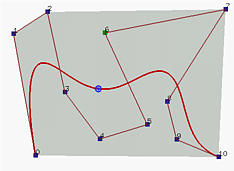
La figura di sinistra mostra due curve di Bézier. La polilinea di colore chiaro rappresenta una curva di Bézier di grado 4, mentre la polilinea di colore scuro rappresenta una curva di Bézier di grado 5. Poiché l'ultima gamba della prima curva e la prima gamba della seconda curva non si trovano sulla stessa linea, le due curve non sono unite in modo liscio. La figura di destra mostra due curve di Bézier che sono tangenti ad una linea nel punto di unione. Tuttavia esse non sono continue di classe C¹. La curva di sinistra è di grado 4, mentre la curva di destra è di grado 7. Tuttavia, il rapporto tra l'ultima gamba della curva di sinistra e la prima gamba della seconda curva sembra vicino a 1 piuttosto che a 7/4=1.75. Per ottenere la continuità di classe C¹ dovremmo aumentare (rispettivamente diminuire) la lunghezza dell'ultima (rispettivamente prima) gamba a sinistra (rispettivamente a destra). Tuttavia esse sono continue di classe G¹.

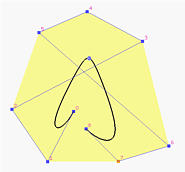
Sussiste un'altra applicazione interessante della proprietà di tangenza. Se il primo e l'ultimo punto di controllo coincidono (cioè P₀ = P_n) e P₁, P₀ e P_n-1 sono collineari, la curva di Bézier generata sarà chiusa e continua di classe G¹ nel punto di unione come mostrato sotto. Per conseguire la continuità di classe C¹ in P₀, dobbiamo avere P₁ - P₀ = P_n - P_n-1 (vale a dire la prima e l'ultima gamba hanno la stessa lunghezza e P₁, P₀ = P_n, P_n-1 sono collineari).

Notare che sebbene la curva sopra somigli ad un'ellisse, tuttavia non lo è perché questa curva è di grado 6 e le curve di Bèzier sono polinomi che non possono rappresentare cerchi ed ellissi.

Una relazione tra la derivata e l'algoritmo di de Casteljau

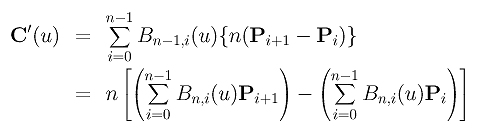
Pertanto la derivata di una curva di Bézier è la differenza tra due curve di Bézier di grado n-1. Per semplicità siano C₁(u) and C₂(u) le due curve:

Da queste definizioni sappiamo che la prima curva C₁(u) è definita dai punti di controllo P₁, P₂, ..., P_n, che la seconda curva C₂(u) è definita dai punti di controllo P₀, P₁, ..., P_n-1, e che la derivata è

Pertanto in teoria per calcolare la derivata di C(u) in un punto particolare u, possiamo usare l'algoritmo di de Casteljau per calcolare C₁(u) e C₂(u). Poi, calcolando la loro differenza seguita da una moltiplicazione per n otteniamo C'(u). Pertanto il punto sulla curva C(u) ed il suo vettore tangente C^'(u) possono essere calcolati contemporaneamente mediante l'algoritmo di de Casteljau.

Ora applichiamo l'algoritmo di de Casteljau per calcolare C₁(u) e C₂(u). Vedi la figura sotto. La colonna più a sinistra ha tutti i punti di controllo assegnati. Il punto n0 fornisce il punto C(u) sulla curva, e il segmento che unisce (n-1)0 e (n-1)1 è l'ultima polilinea di controllo della rete di de Casteljau. Di fatto n0 giace nel segmento di (n-1)0 e (n-1)1 e lo divide secondo il rapporto u:1-u.

Poiché la curva C₁(u) è definita mediante i punti di controllo 01, 02, ..., 0n, usando il diagramma sopra sappiamo che (n-1)1 è il punto sulla curva C₁(u). Analogamente, poiché C₂(u) è definito mediante i punti di controllo 00, 01, ..., 0(n-1), usando il diagramma sopra sappiamo che (n-1)0 è il punto sulla curva C₂(u). Pertanto il vettore C₁(u)-C₂(u) è il vettore dal punto (n-1)0 al punto (n-1)1, e la derivata di C(u) è n volte C₁(u)-C₂(u).

Cosa significa questo? Poiché il segmento di linea da (n-1)0 a (n-1)1 della rete di de Casteljau ha la stessa direzione del vettore tangente a C(u), risulta tangente alla curva in C(u)! Riassumendo

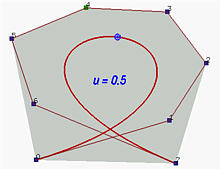
La figura seguente mostra un esempio. Il punto mostrato corrisponde a u = 0.5. Risulta chiaro che l'ultimo segmento della rete di Casteljau è tangente a C(0.5).

Derivate di ordine più alto

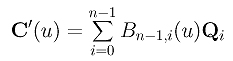
Applicando la formula della derivata alla curva di Bézier sopra si ottiene la seguente, che fornisce la derivata seconda della curva originaria di Bézier:

Dopo aver ottenuto C'(u) e C''(u), la triade mobile e la curvatura in C(u) possono essere calcolate facilmente. Derivate di ordine più alto possono essere calcolate ricorsivamente applicando la formula della derivazione.

Per esprimere le derivate di ordine più alto in forma coincisa, useremo il concetto delle differenze finite. Definiamo D_i⁰ come il punto di controllo P_i per 0 <= i <= n. Definiamo poi la differenza di primo livello D_i¹ come la differenza del precedente livello:

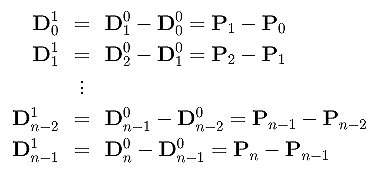
Notare che la differenza di primo livello ha solo n punti, uno in meno del numero dei punti di controllo assegnati. Più precisamente il primo livello della differenza risulta

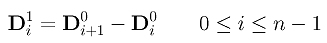
La differenza di secondo livello viene definita come la differenza dei punti di primo livello:

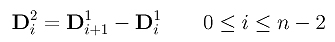
Questa differenza di secondo livello ha n-1 punti. Ripetendo la procedura possiamo definire la differenza di livello k come segue: la differenza di livello k ha n-k+1 punti.

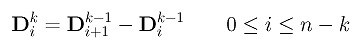
Mediante questa notazione le derivate di ordine più alto possono essere espresse in forma coincisa. Innanzitutto riscriviamo C'(u) come segue, facendo uso dei D_i¹:

Applicando la derivata a C'(u) per calcolare C''(u) otteniamo la formula di C''(u) nei D_i²:

Fare lo stesso a C''(u) per ottenere una formula per C'''(u) nei D_i³:

Continuare il processo e infine calcolare la k-ma derivata C^[k](u) nei D_i^k:

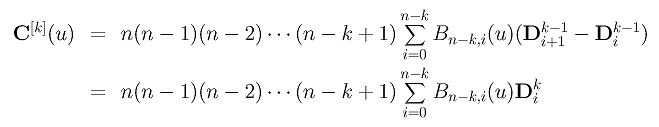
Pertanto per calcolare la derivata k-ma di C(u) in un particolare u, prima calcoliamo i D_i^k e applichiamo l'algoritmo di de Casteljau per calcolare il punto corrispondente a u sulla curva di Bézier definita dai D_i^k. Più precisamente possaimo disporre tutti i D_i⁰ sulla colonna 0, assignare alle frecce in direzione sud-est e nord-est rispettivamente -1 and 1 per calcolare la colonna 1 dei D_i¹. Riopetere la procedura finché si raggiunge la colonna k come mostrato sotto:

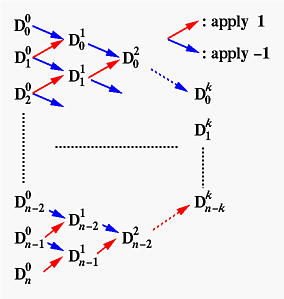
Infine applicare l'algoritmo di de Casteljau ai punti sulla colonna k con u e moltiplicare il risultato per n(n-1)(n-2)...(n-k+1); in tal modo si ottiene il vettore di C^[k](u)!