Costruzione delle Curve di Bézier

Dati n+1 punti P₀, P₁, P₂, ..., P_n nello spazio, i punti di controllo, la curva di Bézier definita da questi punti di controllo è

dove i coefficienti sono definiti come segue:

Pertanto il punto che corrisponde ad u sulla cirva di Bézier è la media "pesata" di tutti i punti di controllo, dove i pesi sono i coefficienti B_n,i(u). I segmenti di linea P₀P₁, P₁P₂, ..., P_n-1P_n, chiamati legs, unendosi in quest'ordine formano una polilinea di controllo. Molti autori preferiscono chiamare questa polilinea di controllo poligono di controllo. Le funzioni B_n,i(u), 0 <= i <= n, vengono chiamate  funzioni base di Bézier oppure polinomi di Bernstein.

Da notare che il dominio di u è [0,1]. Come risultato, tutte le funzioni di base sono non negative. Nella formula sopra, poichè u ed i possono essere entrambi zero, così come 1 - u ed n - i, noi adottiamo la convenzione che 0⁰ vale 1. Il grafico seguente mostra una curva di Bézier definita da 11 punti di controllo, dove il punto blu è un punto della curva corrispondente a u=0.4. Come si può vedere, la curva segue più o meno la polilinea.

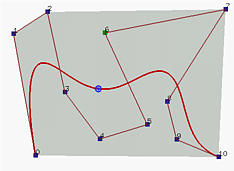
Le seguenti proprietà di una curva di Bézier sono importanti:

1. Il grado di una curva di Bézier definita da n+1 punti di controllo è n:
2. In ogni funzione di base l'esponente di u è i + (n - i) = n. Pertanto il grado della curva è n.
3. C(u) passa per P₀ e P_n:
   Questo è evidente dalla figura. La curva passa per il primo ed ultimo punto di controllo. E' possibile verificarlo analiticamente mediante alcune manipolazioni algebriche.
4. Non negatività:
   Tutte le funzioni di base sono non negative..
5. Partizione dell'Unità:
   La somma delle funzioni di base per un fissato u vale 1. Non è difficile verificare che le funzioni di base sono i coefficienti nell'espansione binomiale dell'espressione 1 = (u + (1 - u))ⁿ. Pertanto la loro somma è 1. Inoltre, poiché sono non negativi, concludiamo che il valore di qualunque funzione di base è compreso tra 0 e 1.
   

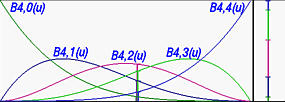
   Nella figura di sinistra abbiamo una curva di Bézier definita in base a 5 punti di controllo. Le sue cinque funzioni di base sono funzioni di u come mostrato nella figura a destra. Le figure mostrano u=0.5 e le cinque funzioni di base. Le linee verticali più a destra mostrano il modo di partizionare 1 in cinque intervalli, da cui il nome di partizione dell'unità. Da notare che il colore di una partizione è identico al colore usato per tracciare la corrispondente funzione di base.

   Poiché tutte le funzioni di base sono comprese tra 0 e 1 e la somma vale 1, esse possono essere considerate come pesi nel calcolo di una media pesata. Più precisamente potremmo affermare che "per calcolare C(u) si prende il peso B_n,i(u) per ciascun punto di controllo P_i e si sommano assieme".

6. Proprietà di HULL convesso:
   Significa che la curva di Bézier definita da n + 1 punti di controllo assegnati giace completamente nell'HULL convesso formato dai punti di controllo.  L'HULL convesso di un insieme di punti è il più piccolo insieme convesso che contiene tutti i punti. Nella figura seguente l'HULL convesso degli 11 punti di controllo è mostrato in grigio. Da notare che non tutti i punti di controllo giacciono sul bordo dell'HULL convesso. Ad esempio i punti di controllo 3, 4, 5, 6, 8 e 9 sono all'interno. La curva, eccetto che per i primi due punti finali, giace completamente nell'HULL convesso.
   

   La proprietà è importante perché siamo garantiti che la curva generata giacerà un una regione capita e calcolabile e non fuoriuscirà da essa.

7. Proprietà della Variazione Diminishing:
   Se la curva giace in un piano, vuol dire che nessuna linea retta interseca una curva di Bézier un numero di volte maggiore di quello che interseca la polilinea di controllo della curva.
   

   Nella figura sopra la linea gialla interseca la curva 3 volte e la polilinea 7 volte; la linea magenta interseca la curva 5 volte e la polilinea 7 volte; la linea ciano interseca la curva e la sua polilinea due volte. E' possibile tracciare altre linee rette per rendersi conto della proprietà..

   Se la curva si trova nello spazio, sarà sufficiente sostituire "linea" con "piano". Potranno verificarsi casi speciali, tuttavia non risulta difficoltoso ricavare un apposito schema di conteggio che tenga conto anche di essi.

   Qual è il significato di tale proprietà? Ci dice che la complessità della curva (vale a dire  i TURNING e i TWISTING) non è maggiore di quella della polilinea di controllo. In altre parole la polilinea di controllo TWISTS e TURNS più frequentemente di quanto non faccia la curva di Bézier, poiché una linea arbitraria atraversa la polilinea di controllo più spesso di quanto non attraversi la curva. Per esempio nella figura sopra la polilinea di controllo risulta più complessa della curva che definisce..

8. Invarianza affine:
   Se alla curva di Bézier si applica una trasformazione affine, il risultato può essere costruito dalle immagini affini dei suoi punti di controllo. Quando vogliamo applicare ad una curva di Bézier una trasformazione geometrica o anche affine, questa proprietà stabilisce che è possible applicare la trasformazione ai punti di controllo, il che è abbastanza semplice, e una volta ottenuti i punti di controllo trasformati la curva di Bézier trasformata é quella definita da questi nuovi punti. Pertanto non dobbiamo trasformare la curva..

Cosa succede se il dominio di u non è [0.1]?

Talvolta il dominio di una curva di Bézier è [a,b] invece che [0,1]. Pertanto si richiede un cambiamento di variabile. Quello che andrebbe fatto è semplicemente convertire una u in [a,b] in una nuova u in [0,1] e usare questa u nelle funzioni di base. La conversione di u in [0,1] può essere fatta come segue:

Inserendo questa u nelle funzioni di base B_n,i(u) produce la seguente formula:

Queste nuove funzioni di base definiscono una curva di Bézier nel dominio di [a,b].

Un breve riassunto

In definitiva, per definire una curva di Bézier di grado n, bisogna scegliere n + 1 punti di controllo nello spazio in modo che indichino approssimativamente la forma della curva richiesta. Se poi il risultato non soddisfa l'attesa, è possibile spostare i punti di controllo.Quando uno o più punti di controllo vengono spostati, la forma della curva di Bézier cambia di conseguenza. Tuttavia la curva giace nell'HULL convesso definito dai punti di controllo (proprietà dell'HULL convesso) e la forma della curva generata risulta meno complessa della polilinea di controllo (proprietà delle variazione DIMINISHING).