

Ricordiamo la definizione delle funzioni di base delle B-spline come segue:

Questo insieme di funzioni base ha le seguenti proprietà, molte delle quali assomigliano a quelle delle funzioni base di Bézier:

Questa osservazione può essere facilmente generalizzata. Infatti, ignorando il cambiamento delle estremità del knot span, per creare un knot di molteplicità k, saranno influenzate k-1 funzioni baseo create a knot of multiplicity k, k-1 basis functions will be affected. La prima perde un knot span, la seconda ne perde due, la terza ne perde tre e così via.
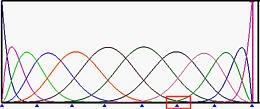
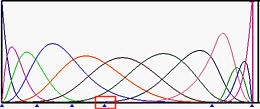
Le figure seguenti mostrano le funzioni base di grado 5 in cui i knots delle estremità sinistra e destra hanno molteplicità 6, mentre tutti i knots nel mezzo sono semplici (Figura (a)). La Figura (b) è il risultato dello spostamento da u5 a u6. Le funzioni base che terminano in u6 hanno il minor numero di knot spans sui quali esse sono non-nulle. Allora, u4 e poi u3 vengono spostati su u6, rendendo u6 un knot di molteplicità 4 (Figure (c) e (d)). La Figura (e) mostra il risultato ottenuto dopo aver spostato u2 su u6, creando un knot di molteplicità 5.
|

|
|
| (a) | (b) | |
|

|
|
| (c) | (d) | |

|
||
| (e) | ||
Nelle figure mostrate sopra, poiché le molteplicità del knot u6 sono 1 (semplice), 2, 3, 4 e 5, i numeri delle funzioni base non-nulle su u6 sono 5, 4, 3, 2 e 1