

In questa pagina saranno discussi nel dettaglio due esempi: uno in cui tutti i knots sono semplici, l'altro dotato di knots multipli.


La seguente tabella fornisce i risultati di tutte le Ni,1(u):
| Funzione di base | Intervallo | Equazione |
| N0,1(u) | [0, 0.25) | 4u |
| [0.25, 0.5) | 2(1 - 2u) | |
| N1,1(u) | [0.25, 0.5) | 4u - 1 |
| [0.5, 0.75) | 3 - u | |
| N2,1(u) | [0.5, 0.75) | 2(2u - 1) |
| [0.75, 1) | 4(1 - u) |
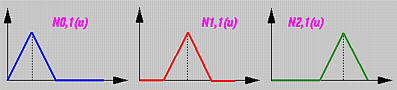
Di seguito vengono mostrati i grafici di queste funzioni base. Poiché i knots interni 0.25, 0.5 e 0.75 sono tutti semplici (cioè, k = 1) e p = 1, ci sono p - k + 1 = 1 funzioni base non-nulle e tre knots. Inoltre, N0,1(u), N1,1(u) e N2,1(u) sono C0 continue nei knots 0.25, 0.5 e 0.75, rispettivamente.
A partire dalle Ni,1(u), si possono calcolare le funzioni base di grado 2. Poiché m = 4, p = 2, e m = n + p + 1, abbiamo n = 1 e ci sono solo due funzioni base di grado 2: N0,2(u) e N1,2(u). La seguente tabella mostra il risultato:
| Funzione di base | Intervallo | Equazione |
| N0,2(u) | [0, 0.25) | 8u2 |
| [0.25, 0.5) | -1.5 + 12u - 16 u2 | |
| [0.5, 0.75) | 4.5 - 12u + 8 u2 | |
| N1,2(u) | [0.25, 0.5) | 0.5 - 4u + 8u2 |
| [0.5, 0.75) | -1.5 + 8u - 8u2 | |
| [0.75, 1) | 8(1 - u)2 |
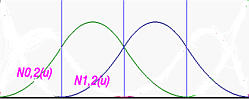
La seguente figura mostra le due funzioni base. Le tre linee verticali blu indicano le posizioni dei knots. Notiamo che ogni funzione base è una curva composta da tre segmenti di una curva di grado 2. Per esempio, N0,2(u) è la curva verde, che è l'unione di tre parabole definite su [0,0.25), [0.25, 0.5) e [0.5,0.75). Questi tre segmenti di curva si uniscono per formare una forma a campana regolare. Verifica che N0,2(u,) (rispettivamente, N1,2(u)) è C1 continua nei suoi knots 0.25 e 0.5 (rispettivamente, 0.5 e 0.75). Come abbiamo detto nella pagina precedente, nei knots, questa curva composita è C1 continua.

Consideriamo un vettore di nodi U = { 0, 0, 0, 0.3, 0.5, 0.5, 0.6, 1, 1, 1 }. Pertanto 0 e 1 hanno molteplicità 3 (cioè 0(3) and 1(3)) e 0.5 ha molteplicità 2 (cioè 0.5(2)). Pertanto m = 9 e l'assegnazione dei nodi risulta
| u0 | u1 | u2 | u3 | u4 | u5 | u6 | u7 | u8 | u9 |
| 0 | 0 | 0 | 0.3 | 0.5 | 0.5 | 0.6 | 1 | 1 | 1 |
Calcoliamo gli Ni,0(u). Osserviamo che poich m = 9 e p = 0 (funzioni di base di grado 0) risulta n = m - p - 1 = 8. Come mostra la tabella sotto esistono solo quattro funzioni di base di grado 0 diverse da 0: N2,0(u), N3,0(u), N5,0(u) e N6,0(u).
| Funzione di base | Intervallo | Equazione | Note |
| N0,0(u) | tutti i valori di u | 0 | poiché [u0, u1) = [0,0) non esiste |
| N1,0(u) | tutti i valori di u | 0 | poiché [u1, u2) = [0,0) non esiste |
| N2,0(u) | [0, 0.3) | 1 | |
| N3,0(u) | [0.3, 0.5) | 1 | |
| N4,0(u) | tutti i valori di u | 0 | poiché [u4, u5) = [0.5,0.5) non esiste |
| N5,0(u) | [0.5, 0.6) | 1 | |
| N6,0(u) | [0.6, 1) | 1 | |
| N7,0(u) | tutti i valori di u | 0 | poiché [u7, u8) = [1,1) non esiste |
| N8,0(u) | tutti i valori di u | 0 | poiché [u8, u9) = [1,1) non esiste |
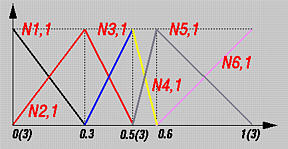
Quindi procediamo con le funzioni di base di grado 1. Poiché p vale 1, n = m - p - 1 = 7. La tabella segunete mostra il risultato:
| Funzione di base | Intervallo | Equazione |
| N0,1(u) | tutti i valori di u | 0 |
| N1,1(u) | [0, 0.3) | 1 - (10/3)u |
| N2,1(u) | [0, 0.3) | (10/3)u |
| [0.3, 0.5) | 2.5(1 - 2u) | |
| N3,1(u) | [0.3, 0.5) | 5u - 1.5 |
| N4,1(u) | [0.5, 0.6) | 6 - 10u |
| N5,1(u) | [0.5, 0.6) | 10u - 5 |
| [0.6, 1) | 2.5(1 - u) | |
| N6,1(u) | [0.6, 1) | 2.5u - 1.5 |
| N7,1(u) | tutti i valori di u | 0 |
La figura seguente mostra i grafici di queste funzioni di base.
Osserviamo in particolare il calcolo di N1,1(u), per esempio. E' ottenuto con la seguente espressione:

Ponendo u1 = u2 = 0 e u3 = 0.3 nell'equazione si ottiene la seguente:
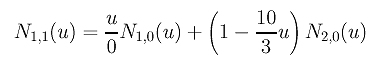
Poiché N1,0(u) è nulla ovunque, il primo termine diventa 0/0, che abbiamo definito valere 0. Pertanto è solo il secondo termine a influire sul risultato. Poiché N2,0(u) vale 1 su [0,0.3), N1,1(u) vale 1 - (10/3)u su [0,0.3).
In seguito, calcoliamo tutti gli Ni,2(u). Poiché p = 2, abbiamo n = m - p - 1 = 6. La tabella seguente contiene tutti gli Ni,2(u):
| Funzione di base | Intervallo | Equazione |
| N0,2(u) | [0, 0.3) | (1 - (10/3)u)2 |
| N1,2(u) | [0, 0.3) | (20/3)(u - (8/3)u2) |
| [0.3, 0.5) | 2.5(1 - 2u)2 | |
| N2,2(u) | [0, 0.3) | (20/3)u2 |
| [0.3, 0.5) | -3.75 + 25u - 35u2 | |
| N3,2(u) | [0.3, 0.5) | (5u - 1.5)2 |
| [0.5, 0.6) | (6 - 10u)2 | |
| N4,2(u) | [0.5, 0.6) | 20(-2 + 7u - 6u2) |
| [0.6, 1) | 5(1 - u)2 | |
| N5,2(u) | [0.5, 0.6) | 12.5(2u - 1)2 |
| [0.6, 1) | 2.5(-4 + 11.5u - 7.5u2) | |
| N6,2(u) | [0.6, 1) | 2.5(9 - 30u + 25u2) |
La figura seguente mostra tutte le funzioni di base di grado 2.

Osserviamo in dettaglio un tipico calcolo, per esempio di N3,2(u). L'espressione è

Ponendo u3 = 0.3, u4 = u5 = 0.5 e u6 = 0.6 si ottiene
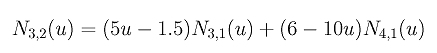
Poiché N3,1(u) è diverso da 0 su [0.3, 0.5) ed uguale a 5u - 1.5, (5u - 1.5)2 è la parte diversa da 0 di N3,2(u) su [0.3, 0.5). Poiché N4,1(u) è diversa da 0 su [0.5, 0.6) ed uguale a 6 - 10u, (6 - 10u)2 è la parte diversa da 0 di N3,2(u) su [0.5, 0.6).
Analizziamo ora la continuità nel nodo 0.5(2). Poichè la molteplicità è 2 e il grado di queste funzioni di base è 2, la funzione di base N3,2(u) è continua di classe C0 in 0.5(2). Questo perché N3,2(u) ha uno spigolo in 0.5(2). Per i nodi diversi dagli estremi, per esempio 0.3, si mantiene la continuità di classe C1 poiché tutti i nodi sono semplici.