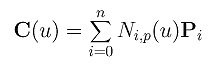

Dati n + 1 punti di controllo P0, P1, ..., Pn e un vettore dei Knot U = { u0, u1, ..., um }, la curva B-spline di grado p definita da questi punti di controllo e dal vettore dei knot U Ŕ
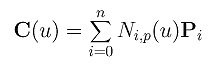
dove le Ni,p(u) sono funzioni base B-spline di grado p. La forma di una curva B-spline Ŕ molto simile a quella di una curva di BÚzier. A differenza di una curva di BÚzier, una curva B-spline coinvolge pi¨ informazioni: un insieme di n+1 punti di controllo, un vettore dei knot di m+1 knots, e un grado p. Notiamo che n, m e p devono soddisfare m = n + p + 1. Pi¨ precisamente, se vogliamo definire una curva B-spline di grado p con n + 1 punti di controllo, dobbiamo fornire n + p + 2 knots u0, u1, ..., un+p+1. D'altra parte,se sono dati un vettore dei nodi di m + 1 knots e n + 1 punti di controllo, il grado della curva B-spline Ŕ p = m - n - 1. Il punto della curva che corrisponde al knot ui, C(ui), Ŕ indicato come un knot point. Quindi, i knot points dividono una curva B-spline in segmenti di curva, ognuno dei quali Ŕ definito su un knot span. Mostreremo che questi segmenti di curva sono tutte curve di BÚzier di grado p nella pagina suddivisione delle curve.
Anche se Ni,p(u) assomiglia a Bn,i(u), il grado di una funzione base B-spline Ŕ un input, mentre il grado di una funzione base di BÚzier dipende dal numero dei punti di controllo. Per cambiare la forma di una curva B-spline, si possono modificare uno o pi¨ parametri di controllo: le posizioni dei punti di controllo, le posizioni dei knots, e il grado della curva.
Se il vettore dei knot non ha alcuna struttura particolare, la curva generata non toccherÓ la prima e l'ultima parte del poligono di controllo come mostrato nella figura sotto a sinistra. Questo tipo di curve B-spline sono chiamate curve B-spline aperte. Possiamo voler stringere la curva in modo tale che sia tangente al primo e all'ultimo segmento nel primo e nell'ultimo punto di controllo, rispettivamente, come avviene per una curva di BÚzier. Per far ci˛, il primo e l'ultimo knot devono avere molteplicitÓ p+1. Questo genererÓ la cosiddetta curva B-spline stretta. Si veda la figura sotto al centro. Ripetendo alcuni knots e punti di controllo, la curva generata pu˛ essere chiusa. In questo caso, l'inizio e la fine della curva generata si uniscono per formare un loop come mostrato nella figura sotto a destra. In queste note, utilizzeremo curve strette.


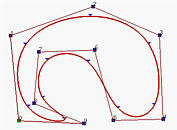
Le figure sopra hanno n+1 punti di controllo (n=9) e p = 3. allora, m deve essere 13 in modo tale che il vettore dei knot abbia 14 knots. Per avere l'effetto stretto, i primi p+1 = 4 e gli ultimi 4 knots devono essere identici. I restanti 14 - (4 + 4) = 6 knots possono essere ovunque nel dominio. Infatti, la curva Ŕ generata con il vettore dei knot U = { 0, 0, 0, 0, 0.14, 0.28, 0.42, 0.57, 0.71, 0.85, 1, 1, 1, 1 }. Osserviamo che tranne per i primi e gli ultimi quattro knots, quelli in mezzo sono quasi uniformemente distribuiti. Le figure mostrano anche il corrispondente segmento di curva su ogni knot span. Infatti, i piccoli triangoli sono i knot points.
