Come detto nella pagina precedente, C(u) può essere vista come l'unione di segmenti di curva definiti su ogni knot span. Nella figura sotto, dove n = 10, m = 14 and p = 3, i primi quattro knots e gli ultimi quattro knots sono stretti e i 7 knots interni sono uniformemente distribuiti. Ci sono otto knot spans, ognuno dei quali corrisponde a un segmento di curva. Nella figura a sinistra in basso, questi knot points sono indicati con triangoli.
Quste proprietà ci consentono di disegnare forme complesse con polinomi di grado più basso. Per esempio, la figura in basso a destra mostra una curva di Bézier con lo stesso insieme di punti di controllo. Non è ancora in grado di seguire il poligono di controllo con esattezza anche se il suo grado è 10!
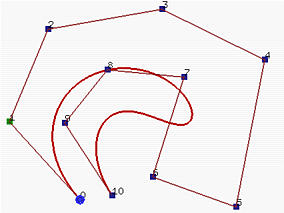
In generale, più basso è il grado, più la curva B-spline si avvicina al suo poligono di controllo. Le seguenti figure utilizzano tutte lo stesso poligono di controllo e i knots sono stretti e uniformemente distribuiti. La prima figura ha grado 7, quella centrale ha grado 5 e la figura a destra ha grado 3. Quindi, poiché il grado diminuisce, la curva B-spline generata si avvicina al suo poligono di controllo.
Infatti ogni punto di controllo ha bisogno di una funzione base e il numero di funzioni base soddisfa m = n + p + 1.
Osservate che la funzione base N0,p(u) è il coefficiente del punto di controllo P0 e è non-nullo nell'intervallo [u0,up+1). Poichè u0 = u1 = ... = up = 0 per una curva B-spline Stretta, N0,0(u), N1,0(u), ...., Np-1,0(u) sono zero e l'unico Np,0(u) è non-nullo (richiamiamo lo schema di computazione triangolare). Di conseguenza, se u = 0, allora N0,p(0) è 1 e C(0) = P0. Un'analoga discussione mostra che C(1) = Pn
Se u è nello knot span [ui, ui+1), ci sono solo p+1 funzioni base (cioè, Ni,p(u), ... , Ni-p+1,p(u), Ni-p,p(u)) non-nulle su questo knot span. Poichè Nk,p(u) è il coefficiente del punto di controllo Pk, soltanto p+1 punti di controllo Pi, Pi-1, Pi-2, .., Pi-p hanno coefficienti non-nulli. Poichè su questo knot span le funzioni base sono non-nulle e la somma è 1, la loro media "pesata", C(u), deve giacere nel dominio convesso definito dai punti di controllo Pi, Pi-1, Pi-2, .., Pi-p. Il significato di "strong" è che C(u) giace nel dominio convesso più piccolo.
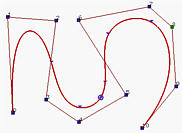
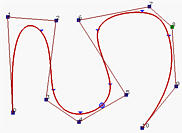
Le due curve B-spline sopra hanno 11 punti di controllo (cioè, n = 10), grado 3 (cioè, p=3) e 15 knots (m = 14) con i primi quattro e gli ultimi quattro knots stretti. Quindi, il numero di knot spans è uguale al numero di segmenti di curva. Il vettore dei knot è
| u0 | u1 | u2 | u3 | u4 | u5 | u6 | u7 | u8 | u9 | u10 | u11 | u12 | u13 | u14 |
| 0 | 0 | 0 | 0 | 0.12 | 0.25 | 0.37 | 0.5 | 0.62 | 0.75 | 0.87 | 1 | 1 | 1 | 1 |
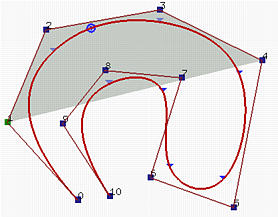
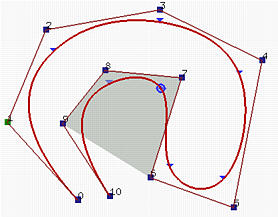
La figura a sinistra ha u nello knot span [u4,u5) = [0.12,0.25) e il corrispondente punto (per esempio C(u)) nel secondo segmento di curva. Quindi, ci sono p+1 = 4 funzioni base non-nulle su questo knot span (per esempio, N4,3(u),N3,3(u), N2,3(u) e N1,3(u) ) e i corrispondenti punti di controllo sono P4, P3, P2 e P1. L'area ombreggiata è il dominio convesso definito da questi quattro punti. E' chiaro che C(u) giace in questo dominio convesso.
La curva B-spline nella figura a destra è definita nello stesso modo. Comunque, u è nell'intervallo [u9, u10) = [0.75,0.87) e le funzioni base non-nulle sono N9,3(u), N8,3(u), N7,3(u) e N6,3(u). I corrispondenti punti di controllo sono P9, P8, P7 e P6.
Di conseguenza, poichè u si muove da 0 a 1 e attraversa un knot, una funzione base diventa zero e una nuova funzione base non-nulla diventa effettiva. Come risultato, un punto di controllo il cui coefficiente diventa zero lascierà la definizione dell'attuale convex hull e sarà sostituito da un nuovo punto di controllo il cui coefficiente diventa non-nullo.
Questo segue da un'altra importante proprietà delle funzioni base B-spline. Ricordiamo che Ni,p(u) è una funzione non-nulla nell'intervallo [ui, ui+p+1). Se u non è in questo intervallo, Ni,p(u)Pi non ha alcun effetto nella computazione di C(u) poichè Ni,p(u) è zero. D'altra parte, se u è nell'intervallo indicato, Ni,p(u) è non-nullo. Se Pi cambia la sua posizione, Ni,p(u)Pi è cambiata e di conseguenza C(u) è cambiata.
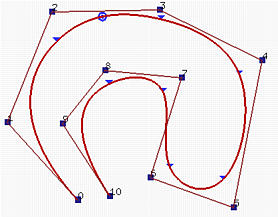
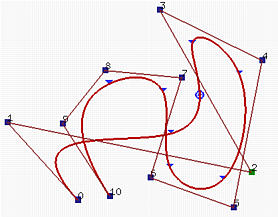
Le curve B-spline sopra sono definite con gli stessi parametri come nel precedente esempio di dominio convesso. Intendiamo muovere il punto di controllo P2. Il coefficiente di questo punto di controllo è N2,3(u) e l'intervallo sul quale questo coefficiente è non-nullo è [u2, u2+3+1) = [u2, u6) = [0,0.37). Poichè u2 = u3 = 0, solo tre segmenti che corrispondono a [u3, u4) (il dominio del primo segmento di curva), [u4, u5) (il dominio del secondo segmento di curva) e [u5, u6) (il dominio del terzo segmento di curva) saranno influenzati. La figura a destra mostra il risultato dello spostamento di P2 all'angolo destro più basso. Come potete vedere, solo il primo, il secondo e il terzo segmento di curva cambiano la loro forma mentre tutti i rimanenti segmenti di curva rimangono nella loro posizione originaria senza alcun cambiamento.
Questo schema di modifica locale è molto importante nel disegno di
curve, perchè possiamo modificare una curva localmente senza cambiare la
forma in modo globale. Questo sarà elaborato nella pagina sullo
spostamento dei punti di controllo.
Inoltre, se è richiesta una curva dalla forma armoniosa, si possono
inserire più knots (e quindi più punti di controllo) così che l'area
influenzata potrebbe essere ristretta ad una regione molto limitata.
Tratteremo dell'inserimento dei knot più in avanti.
Se u non è un knot, C(u) è nel mezzo di un segmento di curva di grado p ed è quindi infinitamente differenziabile. Se u è un knot nel dominio non-nullo di Ni,p(u), poichè l'ultima è soltanto Cp-k continua, così lo è anche C(u).
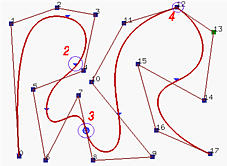
La curva B-spline sopra ha 18 punti di controllo (cioè, n = 17), grado 4, e il seguente vettore dei knot stretti
| da u0 a u4 | u5 | u6 e u7 | u8 | da u9 a u11 | u12 | da u13 a u16 | u17 | da u18 a u22 |
| 0 | 0.125 | 0.25 | 0.375 | 0.5 | 0.625 | 0.75 | 0.875 | 1 |
Così, u6 è un knot doppio, u9 è un knot triplo e u13 è un knot quadruplo. Di conseguenza, C(u) è C4 continua in qualsiasi punto che non sia un knot, C3 è continua in tutti i knots semplici, C2 è continua in u6, C1 è continua in u9, C0 è continua in u13.
Tutti i punti sulla curva che corrispondono ai knots sono segnati con piccoli triangoli. Quelli che corrispondono a knots multipli sono inoltre segnati con cerchi e anche la loro molteplicità. E' molto difficile visualizzare la differenza tra C4, C 3 e persino la C2 continuità. Per il caso C1, i corrispondenti punti giacciono su un segmento, mentre il caso C0 forza la curva a passare attraverso un punto di controllo. Ritorneremo su questo argomento più in avanti quando discuteremo dellamodifica dei knots.
Anche per le curve B-spline vale la proprietà della variation diminishing. Se la curva è in un piano (risp., spazio), questo significa che nessuna linea retta (risp., piano) interseca una curva B-spline più volte di quelle che interseca il poligono di controllo della curva.
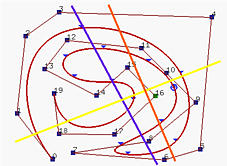
Nella figura sopra, la linea blu interseca sia il poligono di controllo che la curva B-spline 6 volte,mentre la linea gialla interseca il poligono di controllo e la curva B-spline 5 volte. Comunque, la linea arancione interseca il poligono di controllo 6 volte e la curva 4 volte.
If n = p (cioè, il grado di una curva B-spline è uguale a n, il numero di punti di controllo diminuisce di 1), e ci sono 2(p + 1) = 2(n + 1) knots con p + 1 di loro stretti in ogni terminale, questa curva B-spline si riduce a una curva di Bézier.
Anche per le curve B-spline vale la proprietà dell'invarianza. Se è applicata una trasformazione affine ad una curva B-spline, il risultato può essere costruito dall'immagine affine dei suoi punti di controllo. Questa è una proprietà utile. Quando vogliamo applicare una trasformazione geometrica o persino affine a una curva B-spline, questa proprietà stabilisce che possiamo applicare la trasformazione ai punti di controllo, che è molto semplice, e una volta che i punti di controllo sono stati trasformati si è ottenuta la curva B-spline trasformata che è l'unica definita da questi nuovi punti. Quindi, noi non dobbiamo trasformare la curva.
