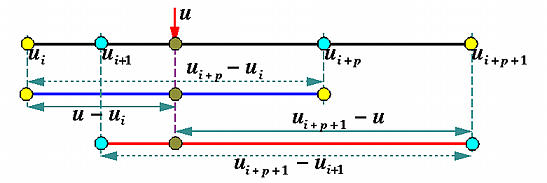
Funzioni Base delle B-spline: Definizione

Le funzioni base di Bézier vengono usate come pesi. Le funzioni base delle B-spline saranno usate nello stesso modo; comunque, esse sono molto più complesse. Ci sono due interessanti proprietà che non riguardano le funzioni base di Bézier, cioè: (1) il dominio viene suddiviso dai knots, e (2) le funzioni base non sono non-nulle sull'intero intervallo. Infatti, ogni funzione base di una B-spline è non-nulla su alcuni sottointervalli adiacenti e, di conseguenza, le funzioni base di una B-spline sono completamente "locali".

Sia U un insieme di m + 1 numeri non-decrescenti, u₀ <= u₁ <= u₂ <= u₃ <= ... <= u_m. Gli u_i sono chiamati knots, l'insieme U si chiama vettore dei knots, e l'intervallo semi-aperto [u_i, u_i₊₁) si chiama i-esimo knot span. Notiamo che poiché alcuni degli u_i possono essere uguali, alcuni knot spans possono non esistere. Se un knot u_i appare k volte (cioè, u_i = u_i₊₁ = ... = u_i+k_-1), dove k > 1, u_i è un knot multiplo di molteplicità k, scritto come u_i(k). Altrimenti, se u_i appare solo una volta, è un knot semplice. Se tra i knots c'è sempre la stessa distanza (cioè, u_i₊₁ - u_i è una costante per 0 <= i <= m - 1), il vettore dei knots (o la sequenza dei knots) è detto uniforme; altrimenti, esso è non-uniforme.

I knots possono essere considerati come punti di divisione che suddividono l'intervallo [u₀, u_m] in knot spans. Si suppone che tutte le funzioni base di una B-spline abbiano il loro dominio su [u₀, u_m]. In questa nota, usiamo spesso u₀ = 0 e u_m = 1 così che il dominio è l'intervallo chiuso [0,1].

Per definire le funzioni base di una B-spline, abbiamo bisogno di un parametro in più, che è il grado di queste funzioni base, p. L' i-esima funzione base di una B-spline di grado p, scritta come N_i,p(u), è definita ricorsivamente come segue:

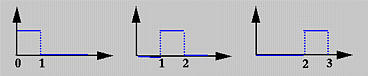
Questa di solito è conosciuta come la formula di ricorsione di Cox-de Boor. Questa definizione sembra complicata; ma, non è difficile da capire. Se il grado è zero (cioè, p = 0), queste funzioni base sono tutte step functions e questo è quello che dice la prima espressione. Cioè, la funzione base N_i_,0(u) vale 1 se u è nell'i-esimo knot span [u_i, u_i₊₁). Per esempio, se abbiamo quattro knots u₀ = 0, u₁ = 1, u₂ = 2 e u₃ = 3, i knot spans 0, 1 e 2 sono [0,1), [1,2), [2,3) e le funzioni base di grado 0 sono N_0,0(u) = 1 su [0,1) e 0 altrove, N_1,0(u) = 1 su [1,2) e 0 altrove, e N_2,0(u) = 1 su [2,3) e 0 altrove. Ciò è mostrato di seguito:

Per capire il modo di calcolare N_i,p(u) per p > 0, usiamo lo schema di calcolo triangolare. Tutti i knot spans sono elencati sulla prima colonna a sinistra e tutte le funzioni base di grado zero sulla seconda. Questo schema è mostrato nel seguente diagramma:

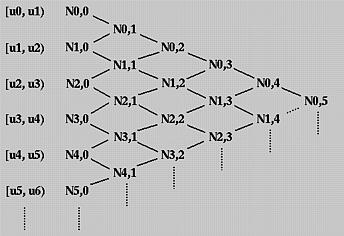
Per calcolare N_i_,1(u), sono richieste N_i_,0(u) e N_i_+1,0(u). Quindi, possiamo calcolare N_0,1(u), N_1,1(u), N_2,1(u), N_3,1(u) e così via. Tutte le N_i_,1(u) sono scritte sulla terza colonna. Una volta che tutte le N_i_,1(u) sono state calcolate, possiamo calcolare le N_i_,2(u) e metterle sulla quarta colonna. Questo processo continua finché tutte le N_i_,p(u) richieste sono state calcolate.

Sopra, abbiamo ottenuto N_0,0(u), N_1,0(u) e N_2,0(u) per il vettore dei knots U = { 0, 1, 2, 3 }. Calcoliamo N_0,1(u) e N_1,1(u). Per calcolare N_0,1(u), poiché i = 0 e p = 1, dalla definizione abbiamo

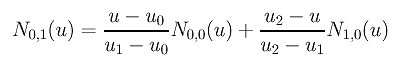
Poiché u₀ = 0, u₁ = 1 e u₂ = 2, la formula sopra diventa

Poiché N_0,0(u) è non-nulla su [0,1) e N_1,0(u) è non-nulla su [1,2), se u è in [0,1) (rispettivamente, [1,2) ), solo N_0,0(u) (rispettivamente, N_1,0(u) ) fornisce un contributo in N_0,1(u). Perciò, se u è in [0,1), N_0,1(u) vale uN_0,0(u) = u, e se u è in [1,2), N_0,1(u) vale (2 - u)N_1,0(u) = (2 - u). Con un calcolo simile si ottiene N_1,1(u) = u - 1 se u è in [1,2), e N_1,1(u) = 3 - u se u è in [2,3). Nella seguente figura, le linee nera e rossa sono rispettivamente N_0,1(u) e N_1,1(u). Notiamo che N_0,1(u) (rispettivamente, N_1,1(u)) è non-nulla su [0,1) e [1,2) (rispettivamente, [1,2) e [2,3)).

Una volta disponibili N_0,1(u) e N_1,1(u), possiamo calcolare N_0,2(u). La definizione ci porta alla seguente formula:

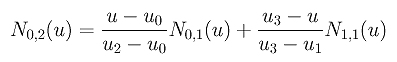
Inserendo i valori dei knots si ottiene

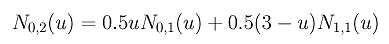
Notiamo che N_0,1(u) è non-nulla su [0,1) e [1,2) e N_1,1(u) è non-nulla su [1,2) e [2,3). Quindi, dobbiamo considerare tre casi:

u è in [0,1):
In questo caso, solo N_0,1(u) fornisce un contributo al valore di N_0,2(u). Poiché N_0,1(u) è u, abbiamo
u è in [1,2):
In questo caso, sia N_0,1(u) che N_1,1(u) forniscono un contributo in N_0,2(u). Poiché N_0,1(u) = 2 - u e N_1,1(u) = u - 1 su [1,2), abbiamo
u è in [2,3):
In questo caso, solo N_1,1(u) fornisce un contributo in N_0,2(u). Poiché N_1,1(u) = 3 - u su [2,3), abbiamo

Se disegniamo il segmento di curva per ognuno di questi tre casi, vedremo che due segmenti di curva adiacenti sono uniti attraverso i knots per formare una curva. Più precisamente, i segmenti di curva del primo e secondo caso si uniscono in u = 1, mentre i segmenti di curva del secondo e terzo caso si uniscono in u = 2. Notiamo che la curva composita mostrata qui è regolare. Ma in generale non è sempre così se un vettore dei knots contiene knots multipli.

Due Osservazioni Importanti

Poiché N_i_,1(u) è calcolata a partire da N_i_,0(u) e N_i_+1,0(u) e poiché N_i_,0(u) e N_i_+1,0(u) sono non-nulle sullo span [u_i, u_i₊₁) e [u_i₊₁, u_i₊₂), rispettivamente, N_i_,1(u) è non-nulla su questi due spans. In altre parole, N_i_,1(u) è non-nulla su [u_i, u_i₊₂). Similmente, poiché N_i_,2(u) dipende da N_i_,1(u) e N_i_+1,1(u) e poiché queste due funzioni base sono non-nulle su [u_i, u_i₊₂) e [u_i₊₁, u_i₊₃), rispettivamente, N_i_,2(u) è non-nulla su [u_i, u_i₊₃). In generale, per determinare il dominio non-nullo di una funzione base N_i,p(u), si può condurre il calcolo usando lo schema di calcolo triangolare fino a raggiungere la prima colonna. Gli spans coperti sono il dominio non-nullo di questa funzione base. Per esempio, supponiamo di voler tirare fuori il dominio non-nullo di N_1,3(u). Sulla base della discussione fatta sopra, possiamo condurre il calcolo nelle direzioni nord-ovest e sud-ovest fino a raggiungere la prima colonna come mostrato con la linea blu tratteggiata nel seguente diagramma. Così, N_1,3(u) è non-nulla su [u₁, u₂), [u₂, u₃), [u₃, u₄) e [u₄, u₅). Oppure, equivalentemente, essa è non-nulla su [u₁, u₅).

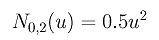
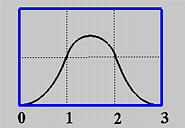
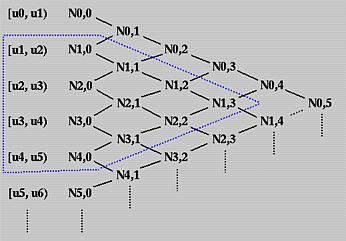
Riassumendo, abbiamo le seguenti osservazioni:

la funzione Base N_i,p(u) è non-nulla su [u_i, u_i+p₊₁). Oppure, equivalentemente, N_i,p(u) è non-nulla su p+1 knot spans [u_i, u_i₊₁), [u_i₊₁, u_i₊₂), ..., [u_i+p, u_i+p₊₁).

In seguito, analizzeremo la direzione opposta. Dato un knot span [u_i, u_i₊₁), vogliamo sapere quali funzioni base useranno questo span nel loro calcolo. Possiamo iniziare con questo knot span e disegnare una freccia obbligata verso nord-est e una verso sud-est. Tutte le funzioni base racchiuse in questa forma a spicchio usano N_i_,0(u) e quindi sono non nulle su questo span. Perciò, tutte le funzioni base di grado p che sono non-nulle su [u_i, u_i₊₁) sono nell'intersezione tra questo spicchio e la colonna che contiene tutte le N_i,p(u). Infatti, questa colonna e le due frecce formano un triangolo equilatero di cui questa colonna è il lato verticale. Contando da N_i_,0(u) a N_i,p(u) ci sono p+1 colonne. Perciò, il lato verticale del triangolo equilatero deve avere al più p+1 entrate: N_i,p(u), N_i_-1,p(u), N_i_-2,p(u), ..., N_i-p_+2,p(u), N_i-p_+1,p(u) e N_i-p_,p(u).

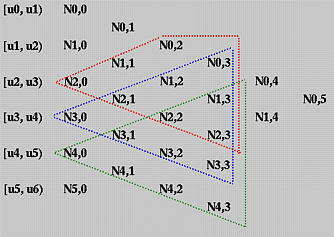
Osserviamo questo diagramma. Per trovare tutte le funzioni base di grado 3 che sono non-nulle su [u₄, u₅), disegniamo due frecce e tutte le funzioni sui lati verticali sono ciò che vogliamo. In questo caso, esse sono N_1,3(u), N_2,3(u), N_3,3(u), e N_4,3(u). Questo è mostrato con il triangolo arancione. Il triangolo blu (rispettivamente, rosso) mostra le funzioni base di grado 3 che sono non-nulle su [u₃, u₄) (rispettivamente, [u₂, u₃) ). Notiamo che ci sono solo tre polinomi di base di grado tre che sono non-nulli su [u₂, u₃).

Riassumendo, abbiamo osservato la seguente proprietà.

Su ogni knot span [u_i, u_i₊₁), al più p+1 funzioni base di grado p sono non-nulle: N_i-p_,p(u), N_i-p_+1,p(u), N_i-p_+2,p(u), ..., N_i_-1,p(u) e N_i_,p(u).

Qual è il significato dei coefficienti

Infine cerchiamo di capire il significato dei coefficienti nella definizione di N_i,p(u). As N_i,p(u) is being computed, it uses N_i,p-1(u) and N_i+1,p-1(u). Il primo è diverso da zero nell'intervallo [u_i, u_i+p). Se u appartiene a quest'intervallo semiaperto, u - u_i rappresenta la distanza tra u e l'estremo sinistro dell'intervallo, la lunghezza dell'intervallo è u_i+p - u_i, e (u - u_i) / (u_i+p - u_i) è il rapporto tra le distanze su menzionate ed è sempre copmpreso tra 0 e 1 (vedere il diagramma sotto). Il secondo termine, N_i,p-1(u), è diverso da zero nell'intervallo [u_i+1, u_i+p+1). Se u appartiene a tale intervallo, allora u_i+p+1 - u rappresenta la distanza tra u e l'estremo destro di qiest'intervallo, u_i+p+1 - u_i+1 è la lunghezza dell'intervallo e (u_i+p+1 - u) / (u_i+p+1 - u_i+1) è il rapporto tra le due distanze, il cui valore è compreso tra 0 e 1. Pertanto N_i,p(u) è una combinazione lineare di N_i,p-1(u) e N_i+1,p-1(u) con due coefficienti, entrambi lineari rispetto a u, compresi tra 0 e 1.