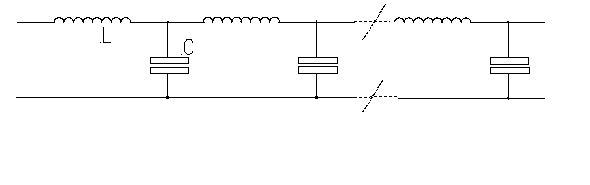
La teoria di base di ogni linea di trasmissione vuole che per avere il massimo trasferimento di potenza, e la minor riflessione di segnale al punto di destinazione, sia rispettata la seguente regola: l'impedenza della sorgente deve essere uguale a quella di destinazione.In altre parole, e in casi reali, deve valere la regola :
impedenza_sorgente=impedenza_cavo=impedenza_ricevitore.
Se la lunghezza del cavo Ŕ inferiore a 1/10 della lunghezza d'onda del segnale che lo attraversa esso pu˛ essere considerato come un normale conduttore, in caso contrario occorre valutare diversamente il suo comportamento.
L'impedenza di un cavo pu˛ essere calcolata tramite la legge di Ohm; che naturalmente Ŕ valida anche a regime alternato (AC):
Z = E / I
A regime alternato la tensione e la corrente ai capi del cavo dipendono appunto dalla sua impedenza che viene definita dalla formula:
Z = sqrt ( (R + 2 * pi * f * L ) / (G + j * 2 * pi * f * c) )
Z = sqrt ( R / (j * 2 * pi * f * L))
Segue che, se la capacitÓ non varia al variare della frequenza, l'impedenza Ŕ inversamente proporzionale alla radice quadrata della frequenza (al crescere di quest'ultima l'impedenza diminuisce ma non linearmente). Questo nella realtÓ si verifica in cavi di politilene, polipropilene e Teflon; polivinile e gomma, invece, diminuiscono la propria capacitÓ al crescere della frequenza.
Quando la frequenza del segnale Ŕ abbastanza elevata i fattori contenenti la f assumono valori significativi tanto che R e G possono essere trascurati; in questo caso l'equazione per il calcolo dell'impedenza diventa:
Z = sqrt ( ( j * 2 * pi * f *L ) / (j * 2 * pi * f * C))
Z = sqrt ( L / C )

L'impedenza di un cavo coassiale non dipende dalla sua lunghezza ma dalle dimensioni dei suoi conduttori, esterno, interno, e dal materiale di cui Ŕ costituito il suo dielettrico. Approssimativamente l'impedenza del cavo pu˛ essere calcolata dall'equazione:
Z = (138 / e^(1/2)) * log ( D / d )
Dove:
Non Ŕ possibile utilizzare un multimetro per misurare l'impedenza di un cavo, quindi Ŕ consigliabile leggere il valore, generalmente stampato su di esso.
Sui segnali audio la massima frequenza si aggira generalmente sui 20Khz, per una lunghezza d'onda di 9,750 m, perchŔ il cavo abbia una sua influenza esso deve essere lungo almeno 4Km! Lo stesso discorso vale per un segnale video (10Mhz circa) su una distanza di 20m.
Quando un segnale viene inviato ad un cavo con un, corretto accoppiamneto, tutta l'energia impiegata viene trasferita al carico. diversamente se uno degli elementi che costituiscono il circuito non Ŕ correttamente accoppiato (cavo o carico), una parte del segnale sarÓ riflessa creando distorsione nel segnale originale.
La velocitÓ di propagazione in un cavo coassiale viene espressa in percentuale rispetto alla velocitÓ della luce nel vuoto e dipende dalle caratteristiche del materiale usato come dielettrico nel cavo.