Sia P(x0,y0) un punto dal quale si voglia tracciare la retta tangente alla parabola. Tale retta sarà una retta del fascio passante per P(x0,y0), l'equazione di tale fascio è
y-y0=m(x-x0)
Imponiamo quindi che il numero di intersezioni tra la parabola e la retta siano due coincidenti, in altri termini il sistema:
![]()
abbia due soluzioni coincidenti, operando una sostituzione si impone infine che il delta dell'equazione in x che si ottiene sia uguale a zero.
A variare della posizione del punto P(x0,y0)rispetto alla parabola si hanno tre possibilità
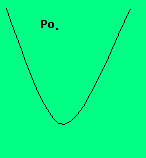 |
Se il punto Po è interno non vi sono rette tangenti |
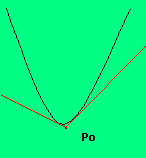 |
se il punto P0 è esterno alla parabola vi sono due rette tangenti |
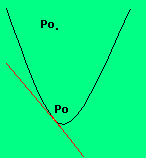 |
se infine P0 è un punto che appartiene al grafico della parabola allora la tangente è unica |
|
Esempio |
Determinare la retta passante per P(0,8) e tangente alla parabola y= - x2+4 |
|
L'equazione del fascio di rette per P è y=mx+8, imponendo che il sistema
sostituendo quindi la prima nella seconda equazione si ottiene l'equazione nel parametro m x2-mx+4=0 il cui D imponiamo che sia nullo, cioè m2-16=0 le cui soluzioni sono m1=-4 a cui corrisponde la retta tangente y= -4x+4 m2=-4 a cui corrisponde la retta tangente y=4x+4
|
|