|
Dati due insiemi A e B, si
chiama relazione di A in B ogni "proprietÓ", che si indica con R,
tale che presi due elementi,
x╬
A
e y╬
B,
la coppia (x,y) pu˛:
| 1)
verificare la proprietÓ R e si scrive xRy |
2)
non verifica la proprietÓ R e si scrive 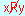 |
In generale una relazione individua un
sottoinsieme del prodotto cartesiano AxB,
ed ha quindi un grafico G ═
A x B.
Esempio
1
Sia
Z l'insieme dei numeri relativi, diremo che due elementi x╬
Z e y╬
Z sono in relazione se verificano la proprietÓ
" x+y=4 ". Se
rappresentiamo in un diagramma cartesiano le coppie (x,y) in relazione si
ottiene, in base alla tabella:
|
x
|
-3
|
-2
|
-1
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
y
|
7
|
6
|
5
|
4
|
3
|
2
|
1
|
0
|
-1
|
-2
|
-3
|
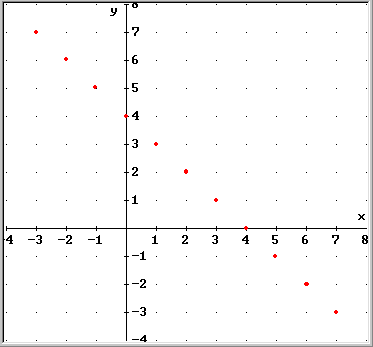
il grafico:
 |
|
Si nota che le coppie che
verificano la relazione sono allineate lungo una retta. Dalla sola conoscenza del grafico di una relazione
si pu˛ risalire alla " formula
matematica" che lega x e y. In questo esempio si nota
l'allineamento, in altri potrebbero apparire evidenti delle simmetrie,
come accade nell'esempio che segue. |
Esempio
2
Sia
A l'insieme dei numeri naturali compresi tra 1 e 100, in tale insieme
consideriamo la relazione:
x
R y se x2+y2 Ŕ un quadrato perfetto
determinando
( con un semplice programma
in Turbo-Pascal) l'insieme G
delle 126 coppie (x,y)
|
G=
|
{
(3,4);
|
(4,3);
|
(5,12);
|
(6,8);
|
(7,24);
|
(8,6);
|
(8,15);
|
(9,12);
|
|
|
(9,40);
|
(10,24);
|
(11,60);
|
(12,5);
|
(12,9);
|
(12,16);
|
(12,35);
|
(13,84);
|
|
|
(14,48);
|
(15,8);
|
(15,20);
|
(15,36);
|
(16,12);
|
(16,30);
|
(16,63);
|
(18,24);
|
|
|
(18,80);
|
(
20,15);
|
(20,21);
|
(20,48);
|
(20,99);
|
(21,20);
|
(21,28);
|
(21,72);
|
|
|
(24,7);
|
(24,10);
|
(24,18);
|
(24,32);
|
(24,45);
|
(24,70);
|
(25,60);
|
(27,36);
|
|
|
(28,21);
|
(28,45);
|
(28,96);
|
(30,16);
|
(30,40);
|
(30,72);
|
(32,24);
|
(32,60);
|
|
|
(33,44);
|
(33,56);
|
(35,12);
|
(35,84);
|
(36,15);
|
(36,27);
|
(36,48);
|
(36,77);
|
|
|
(39,52);
|
(39,80);
|
(40,9);
|
(40,30);
|
(40,42);
|
(40,75);
|
(40,96);
|
(42,40);
|
|
|
(42,56);
|
(44,33);
|
(45,24);
|
(45,28);
|
(45,60);
|
(48,14);
|
(48,20);
|
(48,36);
|
|
|
(48,55);
|
(48,64);
|
(48,90);
|
(51,68);
|
(52,39);
|
(54,72);
|
(55,48);
|
(56,33);
|
|
|
(56,42);
|
(56,90
);
|
(57,76);
|
(60,11);
|
(60,25);
|
(60,32);
|
(60,45);
|
(60,63);
|
|
|
(60,80);
|
(60,91);
|
(63,16);
|
(63,60);
|
(63,84);
|
(64,48);
|
(65,72);
|
(66,88);
|
|
|
(68,51);
|
(69,92);
|
(70,24);
|
(72,21);
|
(72,30);
|
(72,54);
|
(72,65);
|
(72,96);
|
|
|
(75,40);
|
(75,100);
|
(76,57);
|
(77,36);
|
(80,18);
|
(80,39);
|
(80,60);
|
(80,84);
|
|
|
(84,13);
|
(84,35);
|
(84,63);
|
(84,80);
|
(88,66);
|
(90,48);
|
(90,56);
|
(91,60);
|
|
|
(92,69);
|
(96,28);
|
(96,40);
|
(96,72);
|
(99,20);
|
(100,75)}
|
|
|
che verificano la relazione e riportandole in grafico si ottiene
la figura
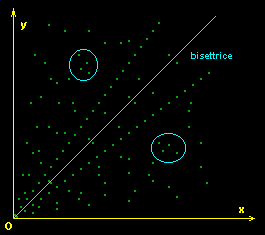 |
Si pu˛ facilmente notare che ci
sono caratteristiche particolari che descrivono la distribuzione dei punti
(in verde) nel
piano cartesiano XOY:
- allineamento
dei punti
- simmetria
rispetto alla bisettrice del quadrante
( si notino ad esempio i punti
cerchiati )
|
|