QUADRATURA DEL CERCHIO
Tra i problemi che hanno appassionato i matematici fin dall'antichità troviamo quelli della della rettificazione della circonferenza (il tentativo cioè di riuscire a determinare un segmento lungo quanto la circonferenza) e della quadratura del cerchio.
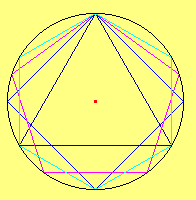
Un tentativo ben riuscito fu quello di Archimede, il quale considerando inizialmente l'esagono regolare inscritto e raddoppiando il numero di lati fino a 96, ottenne un valore molto vicino a quello che adesso si conosce. Egli determinò il valore p = 22/7 = 3,1428.
|
|
All'aumentare del numero dei lati del
poligono si ottiene una approssimazione sempre migliore della misura della
circonferenza e del cerchio.
Tali valori sono gli elementi separatori delle successioni di valori, una crescente e l'altra decrescente, dei perimetri e delle aree dei poligoni regolari inscritti e circoscritti. Questa costruzione suggerisce un metodo per determinare il valore approssimato di p |
Lunghezza della circonferenza: C = 2pR
Area del cerchio: A = pR2
valore approssimato ( venti cifre ) di: p = 3.1415926535897932384
MOTO CIRCOLARE UNIFORME
Un punto materiale si muove di moto circolare uniforme se la traiettoria è una circonferenza e la sua velocità in modulo si mantiene costante. tale punto materiale descriverà archi di circonferenza uguali in tempi uguali.
La direzione del vettore velocità istantanea v è tangente alla traiettoria, il verso dipende da come il punto si muove lungo la circonferenza, il modulo, indicando con T il periodo (tempo che impiega il punto materiale ad effettuare un giro) è dato dalla relazione:
![]()
Il vettore accelerazione istantanea a ha la direzione perpendicolare al vettore velocità, il verso è diretto verso il centro della circonferenza, il suo modulo è:
![]()
Questa relazione si ottiene considerando la definizione di accelerazione e considerando la variazione di velocità che si ha nel periodo T. Si osserva che mentre il punto materiale si muove lungo la circonferenza di raggio R il vettore velocità istantanea descrive una circonferenza di raggio v, allora
![]()
Si osserva che pur non variando il modulo del vettore velocità, esiste una accelerazione.