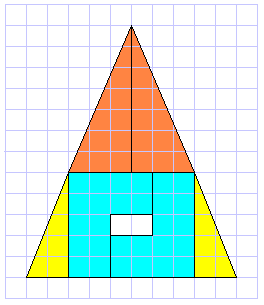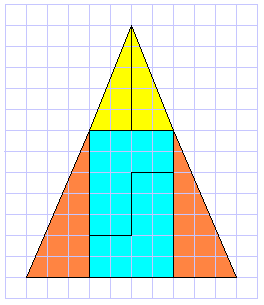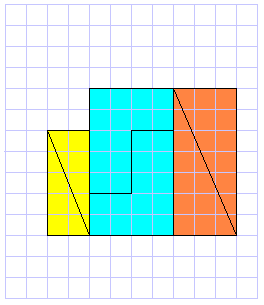
Prendete due triangoli rettangoli con cateti 2 e 5, altri due triangoli rettangoli con cateti 3 e 7 e, infine, due esagoni a forma di "L" aventi area 14, come in figura.

1) Potete sistemare i triangoli maggiori in alto ed i triangoli minori in basso ai lati, occupando lo spazio centrale con gli esagoni che descrivono una superficie libera di area 2: l'area della figura ottenuta dai 6 pezzi sarà (12 x 10)/2 - 2 = 58

2) Potete sistemare i triangoli minori in alto ed i triangoli maggiori in basso ai lati, occupando tutto lo spazio centrale con gli esagoni senza spazi vuoti: l'area ottenuta dai 6 pezzi sarà dunque (12 x 10)/2 = 60

3) Ma se si arrangiano i pezzi come in alto... l'area può misurarsi dalla differenza di aree di rettangoli: (9x7) - (2x2) = 59

Insomma, come mai l'area complessiva delle figure è sempre diversa, pur essendo i pezzi costituenti sempre gli stessi?