Caratteristiche delle onde
	Altezza, Timbro e Intensita'
	Percezione di frequenze diverse
	Campo uditivo e curve isofoniche
	Generazione del suono
	Scale musicali, note e diapason

Schema dell'orecchio

SUONO: variazioni di pressione di un certo mezzo fisico che si percepiscono con l’apparato auditivo.
MEZZO FISICO: prevalentemente aria, ma il suono si propaga anche in acqua e altri materiali.
ONDE: le variazioni di pressione si propagano come ONDE SFERICHE.

Onda sferica vuol dire che se S è la sorgente sonora troviamo che sulle superfici sferiche concentriche ad essa il suono ha le medesime caratteristiche.
Ossia che il segnale generato da S si propaga alla stessa velocità in tutte le direzioni (in ipotesi di mezzo isotropo).

Qualora la sorgente si muova a velocità v troviamo che le onde generate in tempi successivi non sono più concentriche, ma "spostate" verso la direzione del moto.

Quando la sorgente arriva alla velocità del suono essa si muove alla stessa velocità del rumore che genera e quindi sta sul bordo di queste sfere: tutta l’energia "sonora" generata nella direzione del moto si accumula in questo punto.

RISULTATO: non si può stare a lungo in questo punto pena la distruzione della sorgente.

Esempio: il BOOM sonico di un aereo che supera la velocità del suono (MACH1 @ 340m/s @ 1224km/h).

L’onda trasporta con sé energia accumulata in parte sotto forma di ENERGIA CINETICA ed in parte sotto forma di energia elastica di compressione.
La sorgente produce un certo LAVORO sul mezzo con cui è a contatto (l’aria). Quindi la propagazione dell’onda corrisponde ad una propagazione di energia.
Considerando l’energia che attraversa una superficie sferica nell’unità di tempo troveremo la POTENZA erogata dalla sorgente.

L’INTENSITÀ I di un onda è definita come POTENZA/SUPERFICIE=[W]/[m²].

Considerando una superficie A ed un onda che si propaghi perpendicolarmente ad essa ad una velocità v, troveremo che:

• nel tempo D t la perturbazione percorre uno spazio s = v× D t;

• nello stesso tempo attraverso A passa l’energia W× D t = I× A× D t;

• quindi questa energia occupa un volume V = A× s = A× v× D t

La DENSITÀ DI ENERGIA per unità di volume sarà perciò:

E = I× A× D t/(A× v× D t) = I/v

---

CARATTERISTICHE DELLE ONDE

Per lo studio delle onde occorre trovare una rappresentazione matematica dei fenomeni che avvengono.

In questa relazione il termine x rappresenta lo spostamento del fluido (aria o acqua, ad esempio) nella direzione del moto. Si osserva che:

• punti successivi (cioè ad x crescenti) nello spazio presentano spostamenti diversi, mostrando come si muove l’onda di pressione;

• il mezzo non si muove ma oscilla e x ₀ è il valore massimo dell’oscillazione;

• l’onda presenta un andamento sinusoidale sia nello spazio che nel tempo.

Osservando l’onda ad una certa ordinata x, la sua evoluzione nel tempo è rappresentata dal primo grafico.
T ([s]) è detto PERIODO dell’onda, f = 1/T ([Hz]=[s^-1]) è la FREQUENZA mentre w è detta PULSAZIONE. Poiché deve essere w ×T = 2× p segue che:

T = 2×p/w

w= 2× p×f

Osservando l’onda ad un certo istante t si troverà che gli spostamenti del mezzo nello spazio sono quelli rappresentati dal secondo grafico.
l ([m]) è detta LUNGHEZZA D’ONDA. Poiché deve essere k× l = 2× p segue che:

k= 2× p/ l, definito come NUMERO D’ONDA

L’onda si propaga nello spazio ad una certa velocità v. Poiché se mi fermo in un punto dello spazio vedo passare un’onda intera (quindi una lunghezza l) in un tempo T deve essere:

v = l/T

Qualora la sorgente sia in moto verso l’ascoltatore, rispetto ad esso la distanza temporale tra due massimi dell’onda risulta più piccola: IL SUONO HA UNA FREQUENZA PIÙ ALTA. Quindi un treno in movimento genererà, per l’ascoltatore che lo vede avvicinarsi, un suono che risulterà più acuto di quello che sente un ascoltatore solidale al treno stesso. Nella fase di allontanamento si avrà la sensazione opposta: EFFETTO DOPPLER.

---

Sono le caratteristiche di un suono. Al crescere della frequenza di un suono cresce la nostra percezione di ALTEZZA, mentre al crescere della sua intensità abbiamo una percezione di aumento di volume.
Il teorema di scomposizione di Fourier dice che una grandezza PERIODICA può essere considerata come la somma di una serie di grandezze sinusoidali. Il suono si può considerare, nelle maggior parte dei casi, come una grandezza "quasi-periodica", quindi si può scomporre nelle sue componenti sinusoidali. Le diverse frequenze che costituiscono un suono ne definiscono lo SPETTRO. In musica si parla di TIMBRO.
La perturbazione dell’aria si propaga attraverso il MEATO fino al TIMPANO. Questo si muove con la vibrazioni dell’aria e trasmette questo movimento tramite il MARTELLO, l’INCUDINE e la STAFFA alla COCLEA. Quest’ultima è lunga circa 30 mm ed è costituita da circa 30.000 cellule ciliate.
La coclea entra in risonanza con le componenti del suono alle varie frequenze secondo la posizione sulla stessa, come indicato in figura.

Uno spostamento di 3-4 mm lungo la coclea corrisponde alla variazione di frequenza di un ottava.

PERCEZIONE DI FREQUENZE DIVERSE

La modalità di percezione di due frequenze diverse dipende da due fattori:

• FISICO

• NEURALE

Supponiamo di avere due suoni puri (mono-frequenziali). Si distinguono due casi:

I CASO: D f = f₂ - f₁ << f₁

Si dimostra (con le formule di prostaferesi) che il suono risultante dalla somma delle due ha un andamento del tipo:

e ricordando che w = 2 p f segue:

La rappresentazione grafica di questa relazione spiega chiaramente il significato di questa formula:

Si osserva un’onda di frequenza pari alla media delle due MODULATA IN AMPIEZZA da un onda a frequenza più bassa: fenomeno dei BATTIMENTI.
Si percepisce questo fenomeno, ad esempio, quando, accordando le corde di una chitarra, si ha a che fare con note molto vicine.
II CASO: le frequenze sono sufficientemente distanti da non potersi considerare valide le ipotesi che portano alla relazione vista poc’anzi.
Dal punto di vista fisiologico la presenza di due suoni produce due massimi di risonanza distinti lungo la COCLEA.

La capacità di distinguere le due frequenze dipende quindi dalla "risoluzione" della coclea. Ed è proprio questa risoluzione a determinare quando le frequenze sono "sufficientemente vicine" da potersi supporre valida la relazione presentata sopra e quando sono "sufficientemente lontane" da poterla considerare non valida.

Si misura sperimentalmente quello che si vede in figura:

• esiste un campo di valori di f₁, in un intorno sufficientemente piccolo di f₁, in cui si percepisce un solo suono, che è la media dei due;

• se la differenza tra f₁ ed f₂ sta al di fuori di questo intorno ma al di sotto della BANDA CRITICA si è in una zona in cui, prestando attenzione, si possono distinguere rozzamente le due note;

• per frequenze f₁ ed f₂ al di fuori della BANDA CRITICA i due suoni si distinguono nettamente;

Si definiscono alcuni INTERVALLI DI FREQUENZA

SEMITONO: un suono monofrequenziale avente frequenza f₂ si dice essere un semitono sopra ad un suono a frequenza f₁ se f₂ = 16/15 f₁

TONO: f₃ = 9/8 f₁

TERZA MINORE: f₄ = 6/5 f₁

ATTENZIONE: con queste definizioni NON È VERO che un tono si possa considerare la successione di due semitoni. Infatti salire due volte di un semitono rispetto ad una frequenza f₁ corrisponde a moltiplicare questa frequenza per 16/15 due volte, cioè per 256/225 @ 1.1378, mentre salire di un tono corrisponde a moltiplicare per 9/8 = 1.125.

CONSONANZA: si usa per indicare due note che "suonano bene assieme". È chiaro che è un fenomeno SOGGETTIVO e legato all’ascolto: per l’orecchio della nostra epoca è impossibile l’ascolto dei canti gregoriani!

DISSONANZA: note che "non suonano bene assieme".

Le ampiezze della BANDA CRITICA e della zona di percezione mono-frequenziale crescono al crescere della frequenza di riferimento f₁ secondo il seguente grafico:

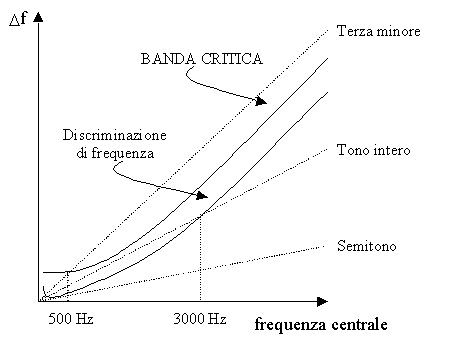
Si noti che gli intervalli di un tono e di un semitono cadono al di sotto della banda critica. Questo è uno dei motivi per cui ascoltando due note aventi uno di questi due intervalli percepiamo una DISSONANZA.
L’intervallo di terza minore, invece, cade al di sotto della banda critica solo per frequenze al di sotto dei 500 Hz ed è, infatti, consuetudine dei musicisti non utilizzare questo intervallo per frequenze basse.
OTTAVA: f₂ = 2 f₁; con questa definizione di ottava si costruiscono varie SCALE (come vedremo più avanti).
ATTENZIONE: se due note si dicessero distanti una o più ottave quando "si percepisce" la stessa nota ma si riconosce che una delle due ha un altezza maggiore (come sarebbe corretto da un punto di vista di definizione "musicale") NON TROVEREMMO LA STESSA COSA!!

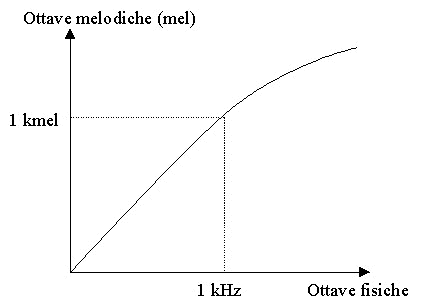
Si è osservato che un aumento di un ottava "percepita" (quindi melodica) corrisponde GENERALMENTE al raddoppio di frequenza. Così il LA a 440 Hz utilizzato per accordare gli strumenti musicali avrà una nota un’ottava sopra a 880 Hz ed una nota un’ottava sotto a 220 Hz.
IN REALTÀ non è proprio così: per frequenze superiori ad 1 kHz si ha la percezione auditiva di una nota un’ottava superiore per incrementi di frequenza superiori al raddoppio. Quindi gli antichi cantanti, ad esempio, dovevano probabilmente sottoporsi a sforzi decisamente maggiori, a parità di spartito!!
Inoltre quando suoniamo brani composti in periodi in cui non esistevano mezzi di registrazione non sappiamo se stiamo suonando realmente le note corrette!!
Noi oggi cosa percepiamo? Percepiamo quello a cui siamo abituati. Infatti il cervello, dove il suono viene elaborato, viene addestrato all’ascolto.

---

CAMPO UDITIVO E CURVE ISOFONICHE

La definizione di intensità va data opportunamente perché la percezione della intensità varia con la frequenza del suono.
L’intensità è espressa quasi sempre in DECIBEL (dB).
Si fissi una intensità di riferimento:

I₀ = 10^-12 [W]/[m²],

che è la soglia di udibilità a 1000 Hz.

Il rapporto I/I₀ indica un valore puramente numerico che si potrà utilizzare per indicare un valore di intensità relativo che sia più significativo di quello assoluto.

Si ha il problema che il campo di variabilità di questo rapporto è molto grande (fino a 7-8 ordini di grandezza), quindi si definisce una nuova unità di misura (il DECIBEL):

IL = 10 log I/I₀ [dB] (Intensity Level)

ESEMPIO: una intensità di 50 dB, che corrisponde al p (piano) musicale, corrisponde ad una intensità (non dB) tale che:

50 = 10 log x

cioè:

log x = 5  >>  x = 10⁵ !!!

Si noti che la soglia del dolore è a 120 dB corrispondenti ad una I mille miliardi (10¹²) di volte più grande di I₀!!!
Poiché la percezione dell’intensità del suono varia con la frequenza, si usano le cosiddette CURVE ISOFONICHE:

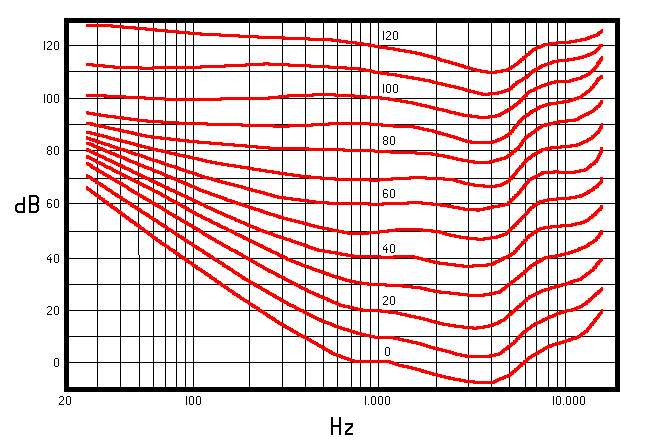
In corrispondenza del punto di maggior sensibilità (3 kHz) si trova il limite inferiore di percezione di ampiezza del timpano: 10^-9 m (l della luce è 0,4-0.7 10^-6 m)!!
Muovendosi lungo ogni curva si trovano per ogni frequenza i valori di IL tali per cui l’ascoltatore medio percepisca una intensità costante.
Queste curve definiscono il LIVELLO DI SONORITÀ (LL: Loudness Level), che si esprime in phon. Quando ci si muove lungo una di queste curve si percepisce una sonorità (un volume) costante, nonostante il valore assoluto di intensità I vari di molti ordini di grandezza.
Tali curve sono tracciate in modo tale che a 1000 Hz il valore di phon ed il valore di IL coincidano.
L'intensità dell'onda è legata alla pressione dell'onda stessa dalla relazione 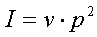, quindi si può scrivere:

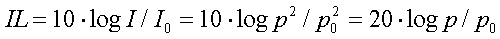
ritrovando, così, la definizione di decibel più usuale.

---

GENERAZIONE DEL SUONO

Gli strumenti musicali possono essere suddivisi in diversi gruppi a seconda del tipo di generazione del suono (escludendo la generazione elettronico-informatica):

• strumenti a fiato;

• strumenti a corde (violino, pianoforte, chitarra);

• strumenti a percussione.

La generazione di suono più interessante (e più semplice) da analizzare è quella a CORDE VIBRANTI. Si tratta di corde elastiche vincolate alle due estremità e soggette ad una certa tensione longitudinale. Queste, opportunamente sollecitate (con un martelletto nel caso del pianoforte, con un plettro o con le dita nel caso della chitarra etc.), si mettono ad oscillare "in un certo modo" per un certo periodo, durante il quale trasmettono, direttamente o tramite terze parti (la chitarra acustica ha una cassa di legno che ne amplifica il suono), la vibrazione all’aria.

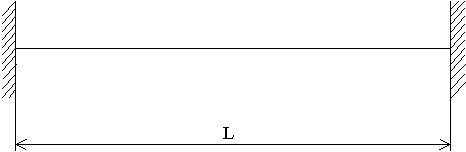
Le onde possono essere generate tendendo trasversalmente la corda (ed in questo modo la si carica con una certa energia potenziale) e lasciandola successivamente andare.
In questo modo nasce una oscillazione composta da un numero teoricamente infinito di onde. Queste sono onde trasversali (nel senso che la perturbazione corrisponde ad un movimento trasversale della corda) e si propagano longitudinalmente. Di questo numero infinito di onde, che si dividerebbero l’energia fornita inizialmente in quantità infinitesime, in realtà ne "sopravvivono" solo alcune: le ONDE STAZIONARIE.
Possiamo definire, semplificando, le onde stazionarie come onde ad energia costante. Quali sono le onde stazionarie su di una corda tesa? Occorre ricordare che le perturbazioni sinusoidali cui facciamo riferimento presentano ventri (massimi e minimi) e nodi (punti in cui la perturbazione assume valore nullo).
E’ intuibile che tutte e sole le onde che presentino nodi in corrispondenza dei vincoli siano tali da conservare la propria energia, mentre le altre si smorzano.
Si osserva che l’onda stazionaria a frequenza più bassa è quella tale per cui l ₁/2 = L. Le successive sono tutte e sole quelle che hanno lunghezza d’onda esprimibile come sottomultiplo intero di l ₁ (l ₁/2, l ₁/3, l ₁/4).

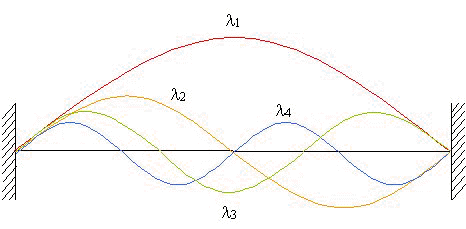
ATTENZIONE: si può quindi osservare che un suono ‘naturale’ è in generale composto da diverse armoniche, che ne caratterizzano il timbro.
Dopo l’armonica fondamentale (l ₁) la prima armonica che si trova è quella a frequenza doppia (l ₂), cioè un’ottava sopra. Quindi segue una frequenza 3 volte maggiore (l ₃) ed una frequenza quattro volte maggiore (l ₄), corrispondente a DUE ottave sopra la fondamentale e così via.
Si può dimostrare che l’energia per le varie componenti armoniche cala al crescere della frequenza della armonica corrispondente.
Il cervello percepisce consapevolmente solo le armoniche a frequenza più bassa, mentre le superiori vengono percepite a livello subliminale.
Consideriamo la definizione di scala di DO maggiore e gli intervalli tra le note espressi in toni e semitoni:

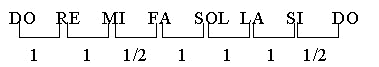
La nota che si trova un semitono sopra il DO si scrive DO# (DO diesis) e quella un semitono sotto si scrive DOb (DO bemolle), e così per tutte la note.
Se la frequenza fondamentale della corda (l ₁) corrispondesse al DO, avremmo che la prima armonica sarebbe il DO ad un ottava superiore (l ₂=l ₁/2). L’armonica successiva, corrispondente a l ₃, corrisponderebbe alla quinta dell’ottava che inizia con l ₂, cioè alla nota SOL a cui segue il DO successivo e così via. L’ordine delle note sarebbe quindi:

DO₁ DO₂ SOL₂ DO₃ MI₃ SOL₃ …

NOTA: l’intervallo di quinta tra una data f₂ ed una f₁ è definito come: f₂ = 3/2 f₁. Si può effettivamente osservare che l ₁ e l ₂ sono tali che f₂ = 3/2 f₁ (si ricorda che f = v/l , dove v à la velocità di propagazione).

L’ACCORDO corrisponde ad un suono composto dalla sovrapposizione di diverse note suonate contemporaneamente.
L’accordo di DO maggiore è costituito dalle tre note: DO MI SOL ed è l’accordo che risulta più ‘naturale’ all’ascolto. Non è banale notare che è costituito proprio dalle prime note che troviamo nella sequenza armonica, segno che pur se percepite a livello subliminale, esse influenzano il nostro concetto di consonanza. Gli accordi costituiti da note corrispondenti ad armoniche successive sono via via meno consonanti sino a darci una sensazione di dissonanza, che comunque è soggettiva (dipende dall’ascolto).
In presenza di segnali di piccola ampiezze (cioè senza distorsione) la percezione simultanea di una nota a frequenza f₂ e di una a frequenza f₃ = 3/2 f₂ crea la sensazione di una f1 =1/2 f₂ (fenomeno di RINTRACCIAMENTO DELLA FONDAMENTALE).

ESEMPIO. Il telefono taglia le armoniche al di sotto dei 300 Hz (fondamentale maschile @ 100Hz, femminile @ 200 Hz), ma l’orecchio ricostruisce le fondamentali partendo dalle armoniche superiori.
A questo punto si può ridefinire l’ALTEZZA di un suono come la fondamentale del suono stesso, dato che anche quando non c’è si ‘sente’ lo stesso!
Anche l’intensità andrebbe ridefinita, visto che la definizione che avevamo visto riguardava i suoni monofrequenziali.

---

SCALE MUSICALI e NOTE

Le composizioni musicali sono costituite da una successione e da una sovrapposizione di note, cioè di suoni di determinate frequenze.
Gia' a Pitagora era noto che due suoni sono gradevoli all'orecchio quando il rapporto tra le loro frequenze (intervallo) è espresso mediante numeri piccoli (1:1 o 2:1 o 3:2, ecc.).
Più piccoli essi sono e migliore è l'accordo; più ci si allontana dai numeri piccoli e maggiore è la dissonanza.
Esistono molti modi per definire una stessa scala. Ad esempio, le note della scala di DO si possono ricavare in diversi modi. Ne vedremo due.

Scala naturale o cromatica:
La scala naturale è costituita da sette note fondamentali: do, re mi, fa, sol, la, si.
Se f è la frequenza (in hertz) della nota fondamentale do, le altre note hanno le frequenze:

do f;  re 9/8f;  mi 5/4f;  fa 4/3f;  sol 3/2f;  la 5/3f;  si 15/8f;  do2 2f.

La nota do2, che ha frequenza doppia di do, inizia un'altra serie di sette note che hanno tra loro rapporti di frequenze uguali a quelli delle precedenti sette note. Ciascuna serie di 7 note si chiama ottava.
L'intervallo tra le stesse note di due ottave successive (intervallo di ottava) è uguale a 2.
La scala è arricchita di note, introducendo i diesis e i bemolle tra due note successive, eccettuato tra il mi e il fa e tra il si e il do dell'ottava superiore.
Si dice diesis di una nota, la nota (più alta) avente con la prima l'intervallo 25/24.
Si dice bemolle di una nota, quella nota (più bassa) che ha con la prima l'intervallo 24/25.
Nella scala naturale gli intervalli tra le note non sono tutti uguali. Alcuni strumenti musicali, come il violino, permettono di produrre tutte le note della scala naturale, non così gli strumenti a tastiera.
Partendo dal SI si ottengono le note salendo di quinta in quinta (una quinta corrisponde ad un intervallo di tre toni più un semitono) trovando FA#, DO#, etc. e poi partendo da FA e scendendo di quinta in quinta e trovando SIb, MIb etc. Realizzando le scale in questo modo succede che il DO# ed il REb, ad esempio, non coincidono.

Per semplificare le cose e per ovviare agli inconvenienti della scala naturale, alla fine del 1600, Andreas Werckmeister (seguito poi da J. Sebastian Bach) introdusse la Scala temperata:
Nella scala temperata gli intervalli tra due note successive sono sempre uguali. L'intervallo di ottava è diviso in 12 intervallini di un semitono ciascuno. L’ottava viene suddivisa in dodici semitoni uguali, per cui l'intervallo di un semitono è pari a:

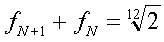  (1,05946). 

• Tra le note do-re, re-mi, fa-sol, sol-la, la-si della scala temperata vi è l'intervallo di due semitoni; tra mi-fa e si-do vi è l'intervallo di un solo semitono.

• Tra due note aventi l'intervallo di due semitoni è intercalata una nota intermedia che corrisponde ai diesis e bemolle della scala naturale.

Se f hertz è la frequenza di do1, è:

do1 f; do# = reþ 1.05946f; re 1.059462f; re# = miþ 1.059463f; ...; do2 1.0594612f.

Nella scala temperata tutti gli intervalli, e quindi le note, risultano alterati rispetto a quelli della scala naturale.
Ad esempio, se f è la frequenza di un do, è:

re naturale: 9/8 f = 1.125f
re temperato: 1.059462f = 1.122f.

Il diapason "naturale":
Finora si è detto soltanto di rapporti tra le frequenze delle diverse note. I valori assoluti di queste frequenze non avrebbero importanza se si eseguissero soltanto pezzi suonati da un solo strumento o cantati da una sola voce. Ma, se si devono eseguire pezzi a più strumenti o a più voci, bisogna partire da un punto comune, cioè accordare tutti gli strumenti a una stessa nota che abbia una ben determinata frequenza.
A questo scopo è stato scelto il la della terza ottava del pianoforte, fissato dalla Accademia delle Scienze di Parigi nel 1858 e confermato dalla Conferenza internazionale di Vienna, con una frequenza pari a 435 hertz.
Tale misura nel 1954 venne innalzata a 440 hertz, valore adottato dall'American Standards Association nel 1936.

Index Sub | Index Demo | Links | Nozioni di Acustica semplice

Servizio segnalazione errori e malfunzionamento del sito - Email: service@sublimen.com
Copyright © 1997- Amadeux - All Rights Reserved Worldwide