MECCANISMO "LEONARD"
OSCILLATORE DI COPPIA MECCANICA
BASATO SU SISTEMA DI BIMANOVELLISMO DI SPINTA
TETRALEVOROTANTE
Il sistema si basa sul meccanismo manovella-glifo ove il glifo anziché oscillare di un certo angolo ruota completamente di un intero angolo giro intorno al proprio centro di rotazione. In pratica si tratta quindi di un glifo rotante e non oscillante.
Per la sua peculiare caratteristica, all'interno del mio meccanismo "Leonard", preferisco denominarlo leva-rotante e non glifo.
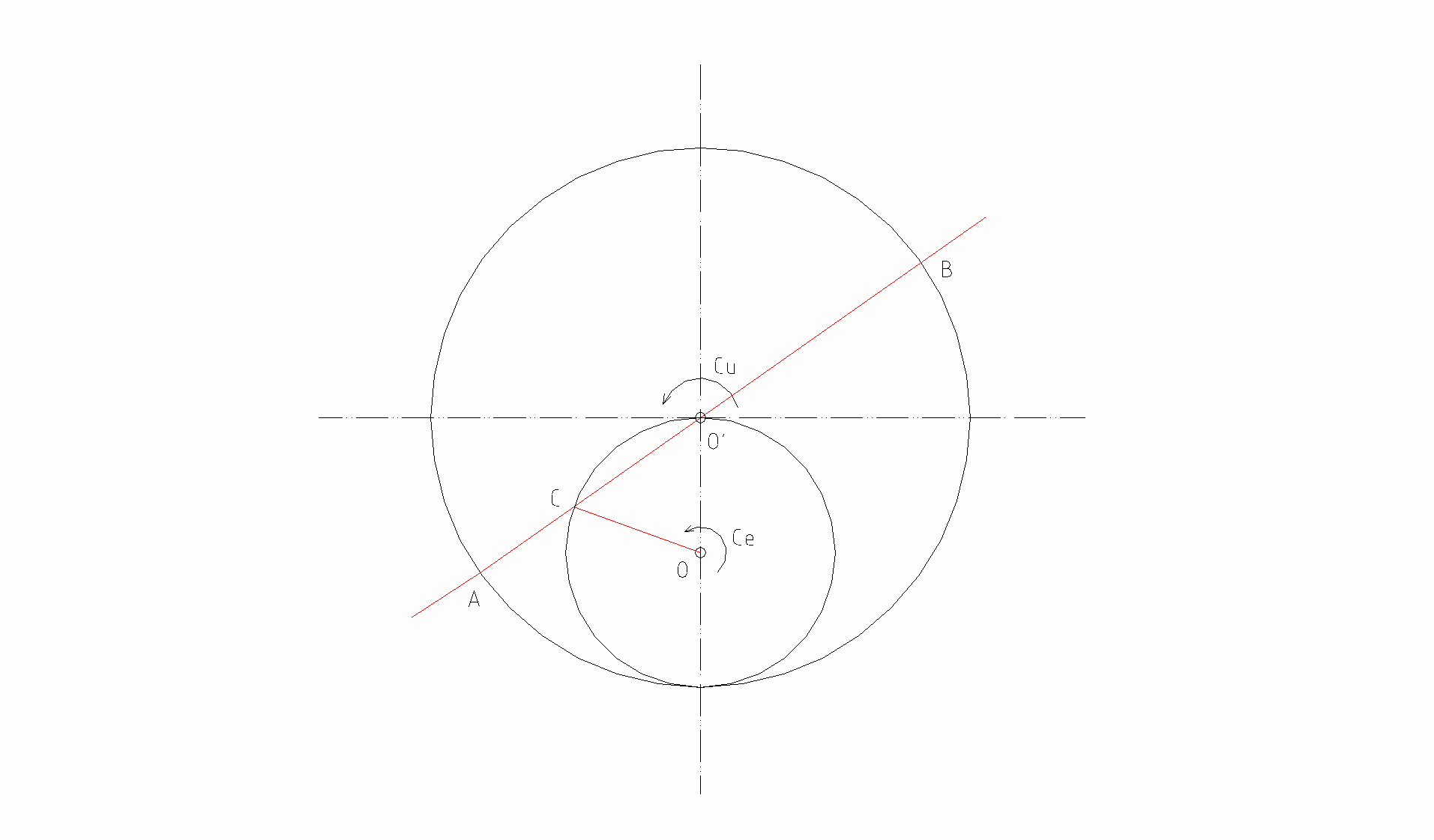
Di seguito è rappresentato lo schema della manovella e della leva-rotante :

La coppia motrice Ce viene applicata in O, centro di rotazione della manovella, e la forza viene trasmessa nel punto C alle due leve-rotanti O'A e O'B le quali trasmettono in uscita la coppia meccanica Cu nel comune centro di rotazione O'. Il raggio del cerchio descritto dalla manovella deve essere necessariamente esattamente la metà del raggio del cerchio descritto dalle due leve-rotanti .
SCHEMA DELLE FORZE E CALCOLO DELLA COPPIA OSCILLANTE IN USCITA
La manovella ruotando trasmette alla leva-rotante la sua componente normale la quale varia da un massimo ad un minimo nullo. La velocità di rotazione delle leve-rotanti è esattamente la metà di quella della manovella. Per fare in modo che le velocità siano uguali occorre introdurre un sistema cambio di velocità con rapporto 2:1 all'albero della manovella.
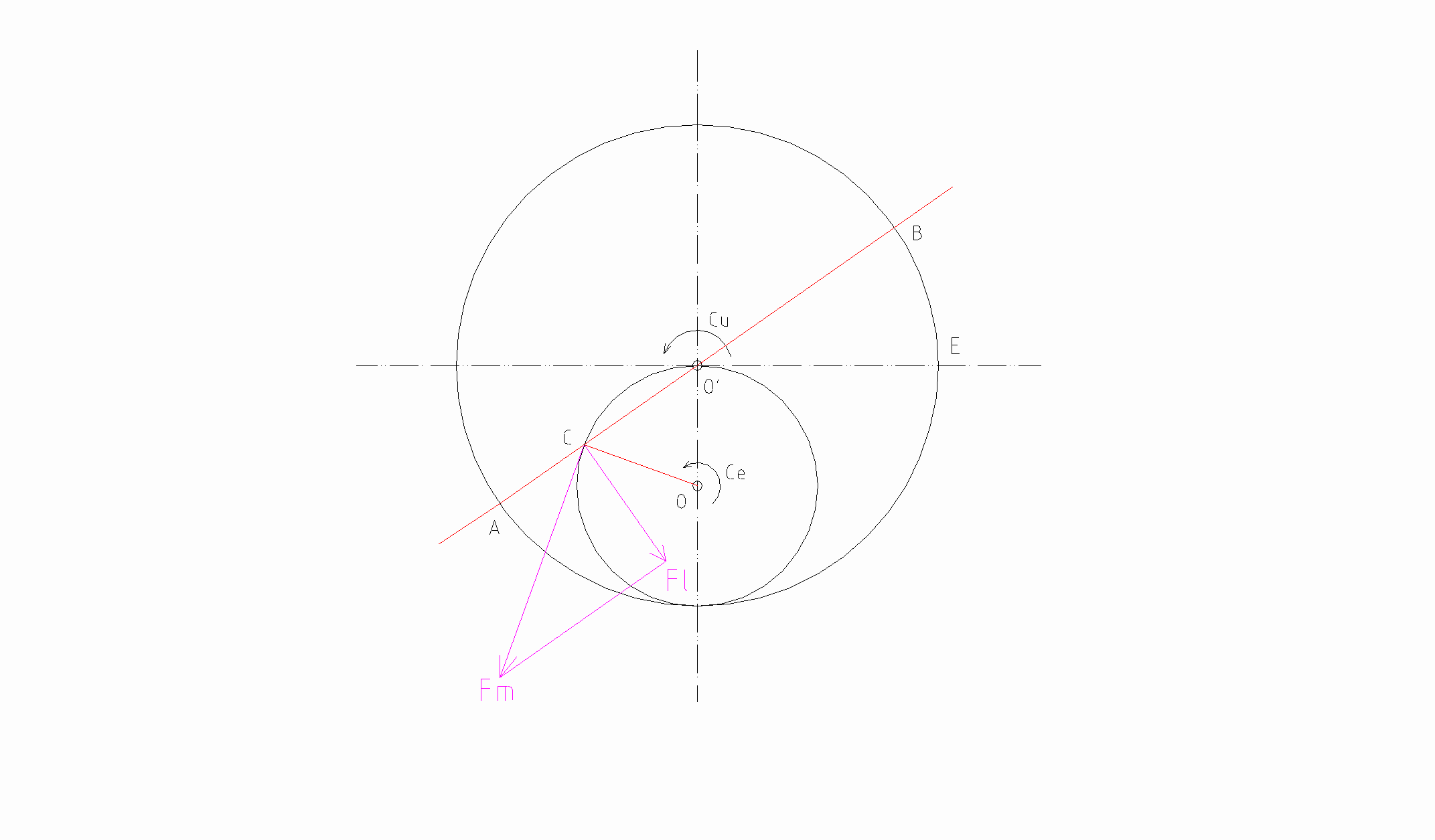
Il valore della forza Fm normale alla manovella si ottiene dividendo il valore della coppia in entrata Ce per la lunghezza della manovella OC ;
infatti il momento meccanico è uguale al prodotto della forza per il braccio; in questo caso si ha che : Ce = Fm * braccio( = lunghezza manovella)
Fm = Ce / OC
La leva-rotante O'B mentre ruota descrive l'angolo j = EO'B
mentre la manovella ruota di un angolo esattamente doppio di j , 2j = O'OC
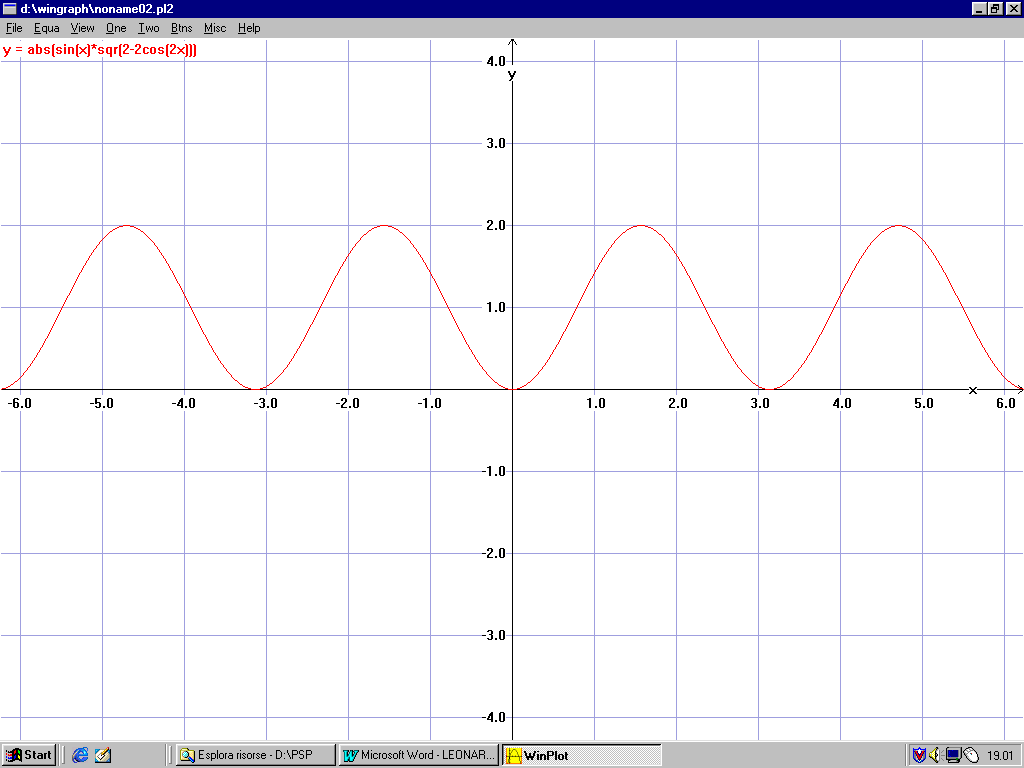
CALCOLO DELLA COPPIA IN USCITA Cu e disegno del suo grafico
Cu = sin (j ) * Rad.quadrata (2-2cos (2j ) )
COLLEGAMENTO DI UNA COPPIA DI MANOVELLE SFASATE DI 120° CON DUE COPPIE DI LEVO-ROTANTI SFASATE DI 60°
Con questo collegamento meccanico si ottiene che :
b) le due coppie ondulatorie in uscita si compongono e originano una nuova
onda di coppia che oscilla in modo sinusoidale intorno al valore doppio di
Ce in entrata di + / - 50 % .
Di seguito riporto lo schema dei due meccanismi accoppiati :

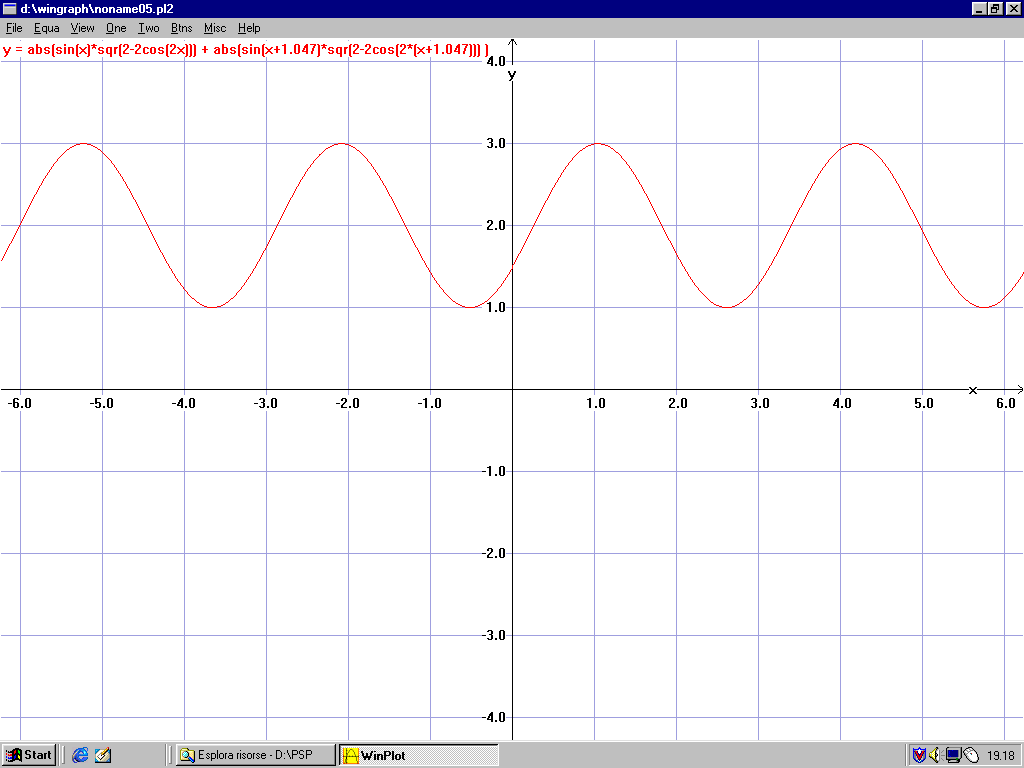
GRAFICO DELLA COPPIA TOTALE IN USCITA AL MECCANISMO
ATTENZIONE : la velocità angolare dell'albero in uscita è esattamente la
metà di quello in entrata per cui la coppia in uscita Cu deve
essere doppia di quella in entrata Ce.
Dal grafico si può constatare, come già detto, che si ha un nuovo tipo di onda di coppia sinusoidale ;
La coppia costante in entrata Ce=1 Nm diventa una coppia oscillante intorno al doppio del valore costante in entrata.
La coppia ha due massimi a 60° e 240° ,Cu = 3 Nm
La coppia ha due minimi a 150° e 330° ,Cu = 2 Nm
VALUTAZIONE IN TERMINE DI POTENZA ENTRANTE E USCENTE
La potenza P è uguale al prodotto della coppia (forza) per la velocità (numero dei giri al minuto).
Potenza in entrata Pe = Ce (costante) * w e
Potenza in uscita Pu = Cu (oscillante) * w u
Le due equazioni suddette sono uguali (convalidando il principio di conservazione dell'energia).
Tuttavia denoto una peculiare caratteristica della seconda equazione ; essa infatti non è il prodotto di due valori costanti come per la prima ; poiché la coppia oscilla, solo il prodotto per il suo valore medio sul giro, per la velocità w u = 0.5 w 2 dà esattamente la potenza in entrata Pe.
Infatti :
valore medio della coppia uscente Cu = 2 Nm
numero di giri all'albero in uscita w u
Pu = 2 * w u
Pe = 1 * w e
Pu = 2 * 0.5 *w e = Pe
Tutto ciò significa che in uscita è più propriamente corretto parlare di potenza istantanea Pi.
La potenza istantanea in uscita presenta come per la funzione ondulatoria della coppia lo stesso andamento ondulatorio con onde (dove la Pi supera la Pe, e valli dove la Pi è inferiore alla alla Pe)
Volendo portare la velocità angolare w u = w e occorre inserire nel meccanismo un dispositivo che cambi la velocità con rapporto di trasmissione 2:1 ;
il raddoppio della velocità dell'albero in uscita comporta ovviamente che la coppia oscillante in uscita Cu venga dimezzata.
Ne consegue il seguente grafico della coppia Cu :

CONSIDERAZIONI SULLA COPPIA-POTENZA IN INTRATA E LA COPPIA-POTENZA IN USCITA
Per la conservazione dell' energia il valore dell' energia in entrata è uguale a quello in uscita.
Tuttavia, essendo la velocità di rotazione dell'albero in uscita perfettamente identico a quello in entrata, lungo il giro la potenza (pur essendo mediamente sul giro identica in valore assoluto alla potenza in entrata) presenta delle onde dove è superiore al valore in entrata (valor medio) e delle valli sinusoidali dove è inferiore al valore in entrata.
Ciò comporta che è corretto parlare per la potenza in uscita di una potenza istantanea di rotazione ; essa infatti presenta due picchi sul giro dove risulta maggiore della potenza media.
E nello stesso tempo dove rappresenta infiniti piccoli picchi superiore alla media e anche infiniti piccoli picchi inferiore alla media.
ur tuttavia, integrando la curva di coppia in uscita, si ottiene che la potenza complessiva che si ha in uscita è identica alla potenza in entrata.
Questo fenomeno dell'uguaglianza della curva di potenza integrata in entrata e in uscita pare che non si realizzi più collegando due o più moduli fra loro in serie.
COLLEGAMENTO DI DUE MODULI "LEONARD" IN SERIE.
Con tale collegamento si verifica un fenomeno fisico particolare :
infatti l'andamento del grafico della coppia viene modificato con tendenza dei picchi intorno a 60° ad elevarsi.