Passeggiate casuali con la TI-92
Roberto Ricci,
Liceo Scientifico "A.Righi", Bologna
Per una lettura corretta del testo occorre avere installato i font di caratteri TI-92 symbols e TI92PC
Molti fenomeni naturali, come il moto delle particelle di un gas, la crescita di polimeri, la trasmissione di un contagio, la diffusione del calore possono essere studiati a partire da un semplice modello, quello delle passeggiate casuali. Lo chiameremo anche moto dell’ubriaco: inizialmente posto nel punto che chiameremo 0 si muove in direzione casuale di un passo costante.
Passeggiate in una dimensione
Per primo analizziamo il caso in cui il moto avviene in una sola direzione: l’ubriaco si muove restando lungo un percorso già segnato, per semplicità rettilineo.
Indichiamo con n il numero dei passi compiuto.
50 ! n
Ogni volta, dopo ogni passo, effettua una scelta casuale: andare nel verso che considereremo positivo, +1, oppure nel verso opposto, ë 1. E’ come lanciare ogni volta una moneta e seguire un verso prefissato o quello opposto a seconda che esca testa oppure croce.
Seq( (ë 1)^Rand(2), i, 1, n) ! aCaso
Le posizioni occupate successivamente per effetto di queste scelte può così essere calcolato come
CumSum(aCaso) ! x
Possiamo rappresentare un digramma orario del moto supponendo che tutti i passi abbiano durata uguale, da considerare come unità di tempo.
Seq( i, i, 1, n) ! t
Quindi passiamo in O Data/Matrix Editor e dopo aver scelto il nome del file Data possiamo inserire t nella colonna c1 e x nella colonna c2.
Per realizzare il grafico, in Plot Setup sceglire Define e quindi porre Plot Type in xyline, Mark in Dot, inserire c1 come x e c2 come y; premere infine ¸ due volte. Dopo aver controllato e eventualmente modificato la $ è possibile visualizzare il diagramma orario con % .
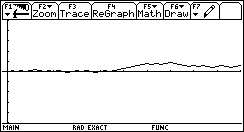
Immaginare anche il diagramma v-t.
Possiamo affrontare lo studio del moto ripetendo tali simulazioni e seguendo una impostazione statistica oppure analizzarlo in modo esatto.
Iniziamo col condurre alcune semplici riflessioni.
Dopo n passi le posizioni raggiunte costituiscono una variabile aleatoria X:
N° di passi |
valori di X: posizioni raggiunte |
1 |
ë 1 , +1 |
2 |
ë 2, 0 , 2 |
3 |
ë 3, ë 1, +1, 3 |
…. |
|
2k |
ë k, … ë 4, ë 2, 0, 2, 4, …, k |
2k+1 |
ë k, … ë 3, ë 1, 1, 3, …, k |
Ciascuna di queste posizioni può essere raggiunta secondo percorsi diversi:
N° di passi |
N° di percorsi che conducono a ogni valore di X |
1 |
1 , 1 |
2 |
1, 2 , 1 |
3 |
1, 3, 3, 1 |
…. |
|
N |
1, C n- 1,0+C n- 1,1, ……C n- 1,i- 1+C n- 1,i ……1 |
Si tratta di uno schema molto noto, il triangolo di Pascal Tartaglia. Questo schema si può anche ottenere reiterando la seguente funzione:
TriTar(ll)
Func
Local ll1,ll2
augment({0},ll)! ll1
augment(ll,{0})! ll2
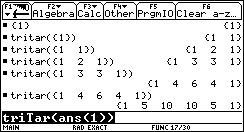Return ll1+ll2
EndFunc
Quei risultati si possono ottenere anche con
Seq(nCr(5,i)/2^n, i, 0, 5)
Essendo nCr(n,i) la funzione predefinita TI-92 che calcola il numero di combinazioni di n elementi i alla volta
Il numero totale di percorsi effettuabili con n passi, la somma dei componenti la riga n-esima del triangolo di Pascal-Tartaglia, è 2n.
Ad es Sum(Seq(nCr(5,i)/2^n, i, 0, 5)) dà 32
Perciò possiamo concludere che la variabile casuale X ha una
legge di distribuzione del tipo 
con i=0,1,…,n. I suoi valori si
possono ottenere anche modificando la funzione TriTar:
TriTar(ll)
Func
Local ll1,ll2
augment({0},ll)! ll1
augment(ll,{0})! ll2
Return (ll1+ll2)/2
EndFunc
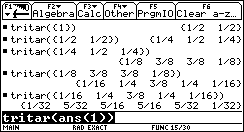
Le posizioni saranno x =ë n+2i. Quindi i = (x+n)/2 ( si osservi che se n è dispari gli x possono essere solo dispari e che se n è pari gli x possono essere solo pari).
Quei risultati si possono ottenere anche con
Seq(nCr(n,i)/2^n, i, 0, n)
Possiamo simulare diverse passeggiate e ottenere per via statistica la distribuzione di probabilità delle X
Seq(Sum(Seq( (ë 1)^Rand(2), i, 1, n)), h,1,20)
Occorre aspettare un po’ i calcoli, e 20 non è un numero elevato
Inserendo ans(1) nella colonna c1 un file Data, si può scegliere di realizzare un grafico con istogramma ottenendo un grafico come il seguente:
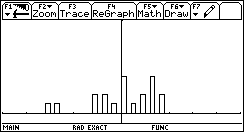
Possiamo piuttosto diminuire il numero di passi, ad esempio 5, e considerare 100 passeggiate.
Otterremmo il grafico seguente a forma di campana:
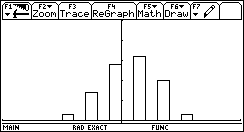
Su questi dati si può effettuare anche qualche elaborazione statistica premendo prima ‡ e poi ‰ :
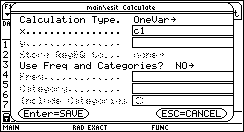
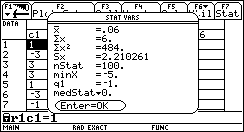
Si può confrontare con la distribuzione teorica.
In particolare la media Xm in una passeggiata di n passi
å ((-n+2i)*nCr(n,i)/2^n,i,0,n)
dà 0, come anche ciascuno dei valori medi di X per passeggiate con k=1,2, …, 10 passi.
seq(å ((-k+2i)*nCr(k,i)/2^k,i,0,k), k, 1, 10)
Si può determinare anche la varianza che è anche il quadrato della distanza quadratica media (X2)m = Xqm2
å ((-n+2i)^2*nCr(n,i)/2^n,i,0,n)
o anche una sequenza di valori utile per congetturare una formula generale
seq(å ((-k+2i)^2*nCr(k,i)/2^k,i,0,k), k, 1, 10)
che dà {1,2,3,4,5,6,7,8,9,10}
Si può approfondire lo studio delle passeggiate casuali in una dimensione affrontando i seguenti quesiti.
1. Studiare la v.c distanza dopo n passi
Seq(|sum(seq(((-1)^rand(2),i,1,n))|,t,1,100)
2. Studiare la v.c. distanza media dopo n passi.
Seq(mean(|cumSum(seq(((-1)^rand(2),i,1,n)))|),t,1,100)
3. Studiare la v.c. numero di volte che si passa per x in una passeggiata di n passi.
Occorrerà realizzare una funzione che conti quante volte in una lista si presenta un certo elemento, diciamo inListR(elem, Lista)
Seq(inListR(x,cumSum(seq(((-1)^rand(2),i,1,n)))),t,1,100)
In particolare studiare la v.c. numero di volte che si passa per l’origine in una passeggiata di n passi.
4. Studiare la v.c. massima distanza raggiunta in una passeggiata di n passi.
Seq(max(|cumSum(seq(((-1)^rand(2),i,1,n)))|),t,1,100)
5. Studiare la v.c. istante in cui per la prima volta si passa per x in una passeggiata di n passi.
Occorrerà creare una funzione che individui dopo quanti posti si presenta per la prima volta un elemento in una lista inListP(elem, lista)
Seq(inListP(x,cumSum(seq(((-1)^rand(2),i,1,n)))),t,1,100)
6. Variare il modello delle passeggiate casuali considerando una diversa probabilità, fissa, nella scelta dei due versi opposti, come se ad esempio il percorso dell’ubriaco fosse tutto in discesa, per cui l’inclinazione rende più improbabile la salita.
Se p è la probabilità di muovere un passo a destra e q quella a sinistra,
p(X=-n+2i)=C(n,i)pi q n-i da cui Xm= (p-q)n e s qm = Ö (4pqn)
7. Variare ancora il modello delle passeggiate casuali considerando una diversa possibilità, che ci possano essere fermate. Ad esempio p¬ = p® = ¼ e pÿ = ½ .
8. Supponiamo che la passeggiata dell’ubriaco avvenga in un vicolo cieco: sia l la distanza massima raggiungibile, raggiunta la quale l’ubriaco è costretto a fare un passo indietro. Quale posizione raggiunge camminando senza posa?
9. Supponiamo che la passeggiata dell’ubriaco avvenga in un vicolo cieco: sia M la posizione massima e m la posizione minima raggiungibile, raggiunte la quale l’ubriaco è costretto a fare un passo indietro. Quale posizione raggiunge camminando senza posa?
10. Indicata con Xi la variabile casuale di valore - 1, +1, con i = 1, 2, 3, … allora la posizione raggiunta dopo n passi è rappresentata dalla variabile casuale Sn = X1 + X2 + … + Xn. Determina media e varianza di Sn a partire da media e varianza di Xi.
11. Possiamo anche vedere le posizioni come i guadagni di un giocatore che scommette 10000 a testa e croce per vincere 20000. Quant’è la sua vincita media
12. Studiare la v.c. guadagno medio dopo n mani
13. Studiare la v.c. dopo quante mani il giocatore va in rovina, ha perso cioè tutto quel che possiede 14. Studiare la v.c. dopo quante mani il giocatore ha sbancato
15. Studiare la probabilità che il giocatore vada in rovina entro un termine determinato possiede (problema difficile da trattare analiticamente ma risolto con ragionamento elegante, detto principio di riflessione, da Desiré André).
Nel dispositivo in figura, proposto a fine ‘800 da Francis Galton, delle palline vengono fatte scendere entro una griglia in cui dei chiodi costituiscono un ostacolo che la singola pallina può aggirare indifferentemente a destra o a sinistra. Ne deriva in modo meccanico un istogramma de descrive la distribuzione delle frequenze delle posizioni raggiunte.
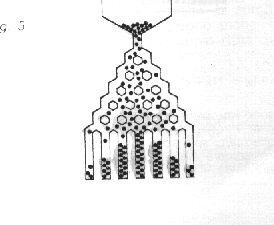
16. Considerare la seguente variante delle passeggiate casuali: viene estratto a caso uno 0 o un 1. Considerate la v.c. che esprime il numero decimale corrispondente al numero decimale che corrisponde a quello binario di n delle cifre ottenute nell’ordine e pari al numero di estrazioni, fissato, n. Oppure al numero decimale corrispondente a 0,…..
17. Simulare l’andamento di un titolo in borsa considerando che possa restare invariato al 25 %, aumentare o diminuire di 1 al 35%, aumentare o diminuire di 2 al 25%, aumentare o diminuire di 3 al 15%.
18. Simulare l’andamento di un titolo in borsa considerando che possa variare al massimo di 3 punti, che nella prima settimana le variazioni siano del tutto casuali, poi l’andamento per le settimane successive sia influenzato dall’andamento della settimana precedente: la probabilità di variare di x sarà pesata con la frequenza con cui la variazione x è avvenuta nella settimana precedente.
19. Se le passeggiate casuali inizialmente considerate possono descriversi anche con un’espressione come x0 = 0 xn = xn-1 ± 1, si possono studiare passeggiate casuali di Fibonacci del tipo x0 = 1, x1=1, xn = ± xn-1 ± xn-2
Passeggiate in due dimensioni
Potremmo applicare il metodo, ben noto e utilizzato in fisica, della scomposizione del moto in due direzioni, preferibilmente quelle ortogonali coincidenti con gli assi di un sistema cartesiano con l’origine nel punto di partenza.
In questo caso le posizioni del piano raggiungibili dall’ubriaco sono quelle di una griglia i cui punti, scelto il passo lungo la direzione x come unitario, hanno tutti coordinate intere.
In questo caso i punti vicini ad una posizione raggiunta sono 8 e i 4 passi in diagonale sarebbero più lunghi degli altri.
Possiamo considerare invece come raggiungibili con un passo solo i quattro punti distanti esattamente un passo.
Consideriamo per iniziare questo secondo modello, di moto in sole due direzioni, per un verso o quello opposto, che potremmo indicare come i quattro punti cardinali E, N, O, S oppure 1, 2, 3, 4.
50 ! n
Ogni volta, dopo ogni passo, effettua una scelta casuale:
Seq(Rand(4), i, 1, n) ! aCaso
Che si traduce in un passo avanti o indietro o in nessun passo in ciascuna delle due direzioni:
Seq((aCaso[i]-2)/2*( (-1)^aCaso[i]-1), i, 1, n) ! dx
Seq((3-aCaso[i])/2*( (-1)^aCaso[i]+1), i, 1, n) ! dy
Per raggiungere posizioni di coordinate
CumSum(dx) ! x
CumSum(dy) ! y
Quindi passiamo in O Data/Matrix Editor e dopo aver scelto il nome del file Data possiamo inserire x nella colonna c1 e y nella colonna c2 per ottenere il grafico della traiettoria.
Volendo analizzare il numero dei diversi percorsi di n passi
1 |
||||||||||||
1 |
o |
1 |
ß |
per |
n = |
1 |
||||||
1 |
||||||||||||
1 |
||||||||||||
2 |
2 |
|||||||||||
1 |
4 |
1 |
ß |
per |
n = |
2 |
||||||
2 |
2 |
|||||||||||
1 |
||||||||||||
1 |
||||||||||||
3 |
3 |
|||||||||||
3 |
9 |
3 |
||||||||||
per |
n = |
3 |
à |
1 |
9 |
o |
9 |
1 |
||||
3 |
9 |
3 |
||||||||||
3 |
3 |
|||||||||||
1 |
Eccetera.
Si tratta di schemi che, ruotati opportunamente, sono generabili anche con una function come la seguente:
genTart (m)
Func
Local zero1,zero2,mm1,mm2,mm3,mm4
newMat(dim(m)[1],1)! zero1
newMat(dim(m)[1]+1,1)! zero2
augment((augment(m,zero1))î ,zero2)! mm1
augment(zero2,(augment(m,zero1))î )! mm2
augment(zero2,(augment(zero1,m))î )! mm3
augment((augment(zero1,m))î ,zero2)! mm4
Return mm1+mm2+mm3+mm4
EndFunc
La function predefinita newMat(nRighe,nColonne)produce una matrice di tutti zero; inoltre mî rappresenta la matrice simmetrica – o trasposta- di m rispetto alla diagonale.
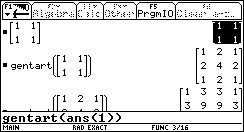
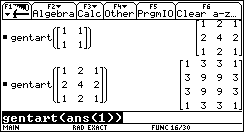
Si riconosce una generalizzazione del triangolo di Tartaglia: una piramide (a base quadrata) di cui ciascuno di questi schemi è sezione parallela alla base.
Si osserva facilmente che se indichiamo con 
questi coefficienti,
allora 
.
Dunque il n° di percorsi di n passi che conducono alla
posizione (x,y) è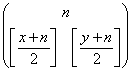 
( si osservi che se n è dispari gli x+y possono
essere solo dispari e che se n è pari gli x+y possono essere
solo pari).
Come già visto in precedenza si possono costruire anche le probabilità modificando leggermente la funzione producendo una media anziché una somma:
genTart (m)
Func
Local zero1,zero2,mm1,mm2,mm3,mm4
newMat(dim(m)[1],1)! zero1
newMat(dim(m)[1]+1,1)! zero2
augment((augment(m,zero1))î ,zero2)! mm1
augment(zero2,(augment(m,zero1))î )! mm2
augment(zero2,(augment(zero1,m))î )! mm3
augment((augment(zero1,m))î ,zero2)! mm4
Return (mm1+mm2+mm3+mm4)/4
EndFunc
Si tratta del valore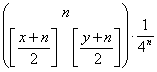 
Infatti il numero di percorsi totali in n passi è 4n.
Può essere istruttivo anche realizzare un programma per simulare dinamicamente una passeggiata di questo tipo, visualizzandone la traiettoria. Il seguente programma produce un output grafico: un punto posizionato al centro di un sistema cartesiano inizia a muoversi appena viene premuto un tasto qualsiasi, fermandosi quando si preme nuovamente un tasto qualsiasi. Si suggerisce di preparare inizialmente una opportuna finestra grafica in ambiente $ .
brownian(passo)
Prgm
Local xx,yy,tasto,aCaso
ClrDraw
0! tasto
0! xx
0! yy
PtOn xx, yy
getKey()! tasto
While tasto=0
getKey()! tasto
EndWhile
0! tasto
While tasto=0
Rand(4) ! aCaso
If aCaso= 1 Then
xx+passo! xx
ElseIf aCaso=2 Then
yy+passo! yy
ElseIf aCaso=3 Then
xx- passo! xx
ElseIf aCaso=4 Then
yy- passo! yy
PtOn xx,yy
EndIf
getKey()! tasto
EndWhile
EndPrgm
L’argomento passo può essere anche un numero non intero. Si provi ad esempio a eseguire brownian(0.1) per avere una simulazione che l’occhio percepisce come più realistica.
Volendo però mettersi nelle condizioni di poter studiare variabili aleatorie con il metodo di Montecarlo, ripetendo cioè un grande numero di volte la simulazione del fenomeno in modo da calcolare le probabilità con impostazione statistica, può essere utile una function come la seguente, concepita per lo studio della distanza raggiunta dopo n passi:
distBrow(nPassi,nProve)
Func
Local xx,yy, listaDist, aCaso, ii, pp
{}à listaDist
For ii,1,nProve
0! xx
0! yy
For pp,1,nPassi
Rand(4) ! aCaso
If aCaso= 1 Then
xx+1! xx
ElseIf aCaso=2 Then
yy+1! yy
ElseIf aCaso=3 Then
xx- 1! xx
ElseIf aCaso=4 Then
yy-1! yy
EndIf
EndFor
Augment(listaDist,{Ö (xx^2+yy^2)})à listaDist
EndFor
Return ListaDist
EndFunc
Essa può essere modificata opportunamente per lo studio di altre variabili aleatorie, di espresse in funzione delle coordinate x e y del punto di arrivo:
vaBrown(nPassi,nProve,espr)
Func
Local xx,yy, listaDist, aCaso, ii, pp
{}à listaDist
For ii,1,nProve
0! xx
0! yy
For pp,1,nPassi
Rand(4) ! aCaso
If aCaso= 1 Then
xx+1! xx
ElseIf aCaso=2 Then
yy+1! yy
ElseIf aCaso=3 Then
xx- 1! xx
ElseIf aCaso=4 Then
yy-1! yy
EndIf
EndFor
Augment(listaDist,{espr| x=xx and y=yy})à listaDist
EndFor
Return ListaDist
EndFunc
Considerare la v.c. distanza finale percorsa in una passeggiata di n passi.
Considerare la v.c. posizione lungo l’asse delle x.