Analisi Combinatoria
con la TI-92
di Roberto Ricci, Liceo Scientifico "A.Righi", Bologna
Il numero di modi per ripartire n elementi in due parti di k e n-k elementi è il binomiale Cn,k se si tiene conto dell’ordine delle parti. Questo deriva immediatamente dal fatto che Cn,k è anche il numero dei sottoinsiemi con k elementi. Altrimenti si può ricondurre la questione a quella di anagrammare la parola S1S1..S1 S2S2..S2 dove il simbolo S1 è ripetuto k volte mentre S2 è ripetuto n- k volte.
Se invece, come è normale parlando di divisioni in parti, non si tiene conto dell’ordine delle parti il loro numero è ancora il binomiale Cn,k se k¹ n- k ovvero n¹ 2k, altrimenti il numero Cn,k/2 / 2.
Dal numero di anagrammi della parola S1S1..S1S2S2..S2…SpSp..Sp i cui simboli sono ripetuti rispettivamente k1, k2, k3, ...,kp volte deriva immediatamente il numero di ripartizioni di un insieme in p sottinsiemi di cui si tenga in conto l’ordine.
Dunque le partizioni di un insieme di elementi in p sottinsiemi S1, S2, S3, ...,Sp rispettivamente di k1, k2, k3, ...,kp elementi, che può essere contato anche come Cn,k1·Cn-k1,k2 ... Cn-k1-k2-...-kp-1,kp, è
![]()
nel caso in cui ki ¹
kj che possiamo indicare anche con C n,k1,k2,…,kp ovvero con 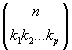 che si può chiamare multinomiale.
che si può chiamare multinomiale.
Altrimenti, se k1 si ripete r1 volte, k2 si ripete r2 volte, .. kp si ripete rp volte,
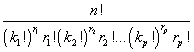
Ad esempio il numero di coppie, anche scompagnate, che si possono fare con n paia di scarpe è ![]() .
.
Il numero totale di bipartizioni di un insieme di n elementi è dunque (2n- 2)/2 = 2n-1 –1 dovendo escludere le coppie (F , S) e (S, F ) dalle coppie (sottinsiemi,complementare) e trascurare l’ordine.
Qual è il numero di tripartizioni di un insieme?
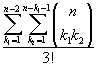
Il numeratore è anche il numero di funzioni suriettive dall'insieme di elementi in questione all’insieme {1,2,3}.
Il numero di tripartizioni di un insieme di n elementi, con n=1,2,3,4,5, si può anche leggere da
Taylor(1/((1-x)(1-2x)(1-3x)),x,1,5)
Qual è il numero di k-partizioni di un insieme di n elementi?
I numeri precedenti si dicono anche numeri di Stirling di 2a specie e si possono indicare con ![]() .
.
Si possono costruire anche con
{1}
{1}
triStir1(ans(1))
{1,1}
triStir1(ans(1))
{1,3,1}
triStir1(ans(1))
{1,7,6,1}
triStir1(ans(1))
{1,15,25,10,1}
La function TrStir1 calcola, data una riga di questo triangolo, la riga seguente:
TriStir1(ll)
Func
Local ll0,ll1,ll2
Seq(n,1,dim(ll))*ll® ll0
augment(ll0,{0})® ll1
augment({0},ll0)® ll2
Return ll1+ll2
EndFunc
Anche i numeri di Stirling hanno una prima proprietà interessante:
![]() .
.
Si può dimostrare anche che
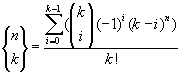
Da notare inoltre che
1 +1x +1x2 +1x3 +1x4 +… = 1/(1- x)
1 +3x +7x2 +15x3 +31x4 +… = 1/((1- x)(1-2x))
1 +6x +25x2 +90x3 +301x4 +… = 1/((1- x)(1-2x)(1-3x))
1 +10x +65x2 +350x3 +1701x4 +… = 1/((1- x)(1-2x)(1-3x)(1-4x))
…
come è facile convincersi verificando che:
(1- x)(1 + x + x2 + x3 + x4 +…) = 1
(1- 2x)(1 +3 x + 7x2 + 15x3 + 31x4 +…) = (1 + x + x2 + x3 + x4 +…)
(1- 3x)(1 +6 x + 25x2 + 90x3 + 301x4 +…) = (1 +3 x + 7x2 + 15x3 + 31x4 +…)
…
Lo si può leggere per le altre diagonali, che possono essere generate con:
{1,1,1,1,1}
{1,1,1,1,1}
cumSum( ans(1)*seq(k,k,1,dim(ans(1)) )
{1,3,6,10,15}
cumSum( ans(1)*seq(k,k,1,dim(ans(1)) )
{1,7,,25,65,140}
cumSum( ans(1)*seq(k,k,1,dim(ans(1)) )
{1,15,90,350,1050}
Si tratta di successioni numeriche
1 1 1 1 1 …
1 3 6 10 15 … n(n+1)/2! …
1 7 25 65 140 … n(n+1)(n+2)(3n+1)/4! …
1 15 90 350 1050 n2(n+1)2(n+2)(n+3)/(2·4!) …
1 31 301 1701 6951 n(n+1)(n+2)(n+3)(n+4)(15n3+30n2+5n-2)/128…
…
come si può calcolare semplicemente con la TI-92 a partire dalla formula
![]() .
.
I primi elementi di tali diagonali si possono ottenere con la TI-92
{1,1,1,1,1,1,1,1}
{1,1,1,1,1,1,1,1}
cumSum( ans(1)*seq(k,k,1,dim(ans(1)) )
Regola per contare
Il numero di ripartizioni di un insieme di n oggetti distinguibili in k parti è S2n,k.
Che succede quando gli oggetti non sono distinguibili tra loro? Ad esempio quando sono tutti uguali, identificabili con degli '1',
Siamo in grado di caratterizzare ciascuna parte solo con la loro somma.
Se non teniamo conto dell'ordine si parla ancora di partizioni, partizioni di un numero intero.
Invece se non teniamo conto dell'ordine si parla di composizioni di un numero intero.
Queste ultime si contano facilmente poiché una composizione è qualcosa del genere: 1-1 1-1; si tratta cioè
di inserire tra gli 1 ad esempio i due simboli trattino '-' e spazio ' ', interpretando il trattino come una
separazione; dunque 2n-1 sono le composizioni del numero n, e Cn-1,k-1 sono quelle che
dividono in k parti.
Invece il numero delle partizioni di un intero è difficile da determinare. Una approssimazione
calcolata dal matematico indiano Ramanujan è epÖ(2n/3)/(4nÖ3).