Analisi Combinatoria
con la TI-92
di Roberto Ricci, Liceo Scientifico "A.Righi", Bologna
Quanti sono i risultati di un'estrazione di 5 oggetti alla volta da un'urna che ne contiene 10 - tutti diversi tra loro ? .
Il numero di risultati diversi possono essere contati, come insegna la II regola per contare, a partire dal numero dei risultati nel caso che gli oggetti, anziché insieme, fossero estratti con 5 estrazioni ordinate di un oggetto alla volta. Sappiamo che queste sono le disposizioni 10·9·8·7·6. Però nel nostro caso due risultati che si diversificano solo per l'ordine debbono essere considerati identici. Ognuna delle 10·9·8·7·6 disposizioni deve perciò essere accomunata con le sue 5! diverse permutazioni. In totale avremo 10·9·8·7·6/5! risultati diversi. Questi risultati si dicono combinazioni di 10 elementi presi 5 alla volta.
Alternativamente si può ragionare nel modo seguente. Associamo un risultato delle nostre estrazioni, ad esempio {1,4,6,7,10}, a uno dei risultati delle estrazioni di tutti gli oggetti dall’urna {Ö
,Ö
,Ö
,Ö
,Ö
,-,-,-,-,-}, nel nostro caso{Ö
,-,-,Ö
,-,Ö
,Ö
,-,-Ö
} ovvero uno degli anagrammi della stringa Ö
Ö
Ö
Ö
Ö
-----. Vi è una corrispondenza biunivoca. I risultati nel secondo caso, come già visto, sono ![]() .
.
In generale dunque le combinazioni di n elementi presi k alla volta, che possiamo indicare con Cn,k, sono in numero pari al rapporto nDs(n,k)/nDs(k,k), ovvero nDs(n,k)/k!, che nella TI-92 si calcola con una function predefinita: nCr(n,k).
Ad esempio:
nCr(10,5) 252
Tale numero Cn,k si può anche scrivere nella forma seguente:
![]()
Questi numeri possiamo trovarli anche nello schema prodotto da
{1}
{1}
tritar(ans(1))
{1,1}
tritar(ans(1))
{1,2,1}
tritar(ans(1))
{1,3,3,1}
detto triangolo di Pascal-Tartaglia
La function Tritar calcola, data una riga di questo triangolo, la riga seguente:
Tritar(ll)
Func
Local ll1,ll2
augment(ll,{0})® ll1
augment({0},ll) ® ll2
Return ll1+ll2
EndFunc
Altri esempi
Gli stessi numeri si possono anche ottenere anche come coefficienti dei termini dello sviluppo della potenza di un binomio (a+b)n, e si dicono perciò binomiali.
Ad esempio:
Expand((a+b)^4) a4 + 4·a3b + 6·a2b2 +4·ab2 + b4
Per capirne la ragione si confronti infatti il calcolo precedente con
Expand((a1+b1)(a2+b2)(a3+b3)(a4+b4))
O anche con
Expand((si1+no1)(si2+no2)(si3+no3)(si4+no4))
Che mette più direttamente in relazione con le combinazioni degli elementi 1,2,3,4.
Vale la pena di osservare inoltre che
2n = (1+1)n = å nCr(n,i)
Tali numeri si indicano anche con l'espressione ![]() che si legge "n su k" oppure "n sopra k".
che si legge "n su k" oppure "n sopra k".
Dal modo con cui vengono ottenuti nel triangolo di Pascal-Tartaglia si capisce che vale l'interessante relazione:
![]()
Tale funzione conta evidentemente anche il numero di sottinsiemi di Sn con esattamente k elementi. Vale la pena di osservare che in numero totale di tali sottinsiemi è dunque 2n=å nCr(n,i) .
Il triangolo di Pascal-Tartaglia è una configurazione numerica poliedrica.
Lo si può leggere per diagonali, che possono essere generate con:
{1,1,1,1,1}
{1,1,1,1,1}
cumSum( ans(1) )
{1,2,3,4,5}
cumSum( ans(1) )
{1,3,6,10,15}
cumSum( ans(1) )
{1,4,10,20,35}
Si tratta di successioni numeriche
1 1 1 1 1 … Cn,n …
1 2 3 4 5 … Cn+1,n = (n+1)/1! …
1 3 6 10 15 … Cn+2.n = (n+1)(n+2)/2! …
1 4 10 20 35 … Cn+3,n = (n+1)(n+2)(n+3)/3! …
…
Notare che ciascun numero è la somma di quelli che lo precedono nella riga precedente
![]()
ovvero anche
![]()
come l’n-esimo numero triangolare (nella terza riga) è la somma dei primi n numeri naturali.
Da notare inoltre che
1 +1x +1x2 +1x3 +1x4 +… = 1/(1- x)
1 +2x +3x2 +4x3 +5x4 +… = 1/(1- x)2
1 +3x +6x2 +10x3 +15x4 +… = 1/(1- x)3
1 +4x +10x2 +20x3 +35x4 +… = 1/(1- x)4
…
come è facile convincersi verificando che:
(1- x)(1 + x + x2 + x3 + x4 +…) = 1
(1- x)(1 +2 x + 3x2 + 4x3 + 5x4 +…) = 1 + x + x2 + x3 + x4 +…
(1- x)(1 +3 x + 6x2 + 10x3 + 15x4 +…) = 1 + 2x + 3x2 + 4x3 + 5x4 +…
…
Si osservi inoltre che la riga asse di simmetria del triangolo, č formata dai numeri:
1, 2, 6, 20, … C2n,n
e a fianco
1, 3, 10, 35, … C2n+1,n
1, 4, 15, 56, … C2n, n- 1
1, 5, 21, … C2n+1, n- 1
1, 6, 28, … C2n,n- 2
…
Può essere interessante anche sistemare i numeri del triangolo in una sequenza in modo naturale:
1, 1, 1, 1, 2, 1, 1, 3, 3, 1, 1, 4, 6, 4, 1, 1, 5, …
notando che Cn,k va a occupare la posizione n(n+1)/2 + k e viceversa, considerando che
t = floor(![]() )
)
è l’indice del più grande numero triangolare minore di n, nella posizione n troviamo il binomiale 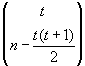
Diverso è il problema di generare le diverse combinazioni.
Possiamo considerare il seguente algoritmo per costruire la combinazione successiva nell'ordine alfabetico di una sequenza di lettere o meglio di numeri diversi (in questo caso l'ordine si dice lessicografico).
Detta a1 , a2 , a3 , …, ak-1 , ak la sequenza di numeri compresi tra 1 ed n:
Ad esempio ecco la traccia di esecuzione dell'algoritmo nel caso della sequenza 2467 per n=7 e quindi k=4:
confrontando con n-k+1, n-k+2, n-k+3, n-k+4 che formano la sequenza 4567 si ha i=2
da 2467 si passa a 2567
da 2567 si passa a 2567
mentre quella ancora seguente:
confrontando 2567 con la sequenza 4567 si ha i=1
da 2567 si passa a 3567
da 3567 si passa a 3456
mentre quella ancora seguente:
confrontando 3456 con la sequenza 4567 si ha i=4
da 3456 si passa a 3457
da 3457 si passa a 3457.
Possiamo creare una function che, dato un numero e una lista che rappresenti una combinazione dei primi n numeri naturali costruisca la lista seguente nell'ordine lessicografico
combSucc(lst,n) Func Local nn, ii, jj, kk n® nn dim(lst) ® kk kk ® ii While lst[ii] ³ nn – kk + ii ii-1® ii EndWhile Lst[ii]+1® lst[ii] 1® jj While ii+jj £ kk Lst[ii]+jj® lst[nn+jj] jj+1® jj EndWhile Return lst EndFunc
Le combinazioni si possono generare anche per via algebrica.
Ad esempio con la calcolatrice simbolica:
Expand( (1+a·x)·(1+b·x)·(1+c·x) )
Il coefficiente del termine di 3° grado in x è l'unica combinazione dei tre elementi a, b e c presi tre alla volta, i tre termini a coefficiente di quello di 2° grado in x sono le combinazioni dei tre elementi a, b e c presi due alla volta, e così via.
Si potrebbe anche costruire una function per avere l'elenco dei coefficienti di un polinomio
coeffPol(pol)
Func
Local coef,lstcoef
pol|x=0 ® coef
{coef}® lstcoef
(pol – coef)/x® pol
While string(pol) ą"0"
pol|x=0® coef
augment({coef }, lstcoef)® lstcoef
(pol – coef)/x® pol
EndWhile
Return lstcoef
EndFunc
E quindi utilizzarla eventualmente con
CoeffPol (pol)[n+1]
per avere quelli dei monomi di grado n.
Ad esempio
Expand(coeffPol(1+a·x)·(1+b·x)·(1+c·x)))
{a·b·c, a·b+a·c+b·c, a+b+c, 1}