Roberto Ricci
Liceo Scientifico "A Righi", Bologna
Procedimenti ricorsivi
Un noto tipo di approccio alla risoluzione dei problemi consiste in un'analisi che conduce alla scomposizione del problema in sottoproblemi più semplici. Può essere descritto nel modo seguente:
Risolvere il problema P:
se si conosce una risoluzione di P
allora applicarla altrimenti scomporre P in sottoproblemi P1, P2, ...,Pn risolvere il problema P1 ...... risolvere il problema Pn
Quando almeno uno dei sottoproblemi è dello stesso tipo del problema in esame si ha una descrizione nota come ricorsiva. Ad esempio i famosi paradossi di Zenone sono legati a descrizioni ricorsive. Il paradosso di Achille e la tartaruga è legato, ad esempio, a una descrizione come la seguente:
Inseguire la tartaruga che ha vantaggio d: percorrere lo spazio d inseguire la tartaruga che ha vantaggio dиvt/vA
dove vA e vt sono rispettivamente la velocità di Achille e quella della tartaruga, con vA > vt. Molto noto è anche il paradosso dell'impossibilità del movimento, basato sulla descrizione seguente:
Andare dal punto A al punto B: andare dal punto A al punto medio del segmento AB andare dal punto medio del segmento AB al punto B.
Tali descrizioni sono in effetti paradossali, o meglio non corrispondono a procedimenti effettivamente realizzabili. Un procedimento effettivamente realizzabile analogo all'ultimo citato è descritto di seguito.
Andare dal punto A al punto B: se la distanza AB è superiore a un passo allora andare dal punto A al punto medio del segmento AB andare dal punto medio del segmento AB al punto B altrimenti fare un passo da A a B.
Curve ricorsive
A volte, dovendo tracciare a mano libera un segmento di estremi assegnati e troppo lontani tra loro per la nostra mano insicura, può capitare di seguire un procedimento come il seguente
Congiungere A e B con un segmento: se A e B sono abbastanza vicini allora tracciare il segmento AB altrimenti individuare il punto medio M del segmento AB congiungere A e M con un segmento congiungere M e B con un segmento.
Tale procedimento ha la stessa struttura dell'ultimo descritto nel paragrafo precedente, derivato dal paradosso di Zenone sull'impossibilità del movimento.Semplicemente per il gusto di generalizzare si potrebbe variare il procedimento nel modo seguente
Congiungere A e B: se A e B sono abbastanza vicini allora tracciare il segmento AB altrimenti individuare mediante un assegnato criterio, [riferito ad AB, un punto qualsiasi C congiungere A e C congiungere C e B.
Si capisce subito che non è un "buon procedimento",
che originerebbe facilmente una linea divergente, a meno di non sottoporre a
delle limitazioni le distanze ![]() e
e ![]() .
Se imponessimo ad esempio che
.
Se imponessimo ad esempio che ![]() =
=![]() =
=![]()
![]() otterremmo una linea, una curva ricorsiva, approssimativamente uguale a quella
della figura seguente:
otterremmo una linea, una curva ricorsiva, approssimativamente uguale a quella
della figura seguente:

Ancora per il piacere di generalizzare si può esaminare il procedimento seguente:
Congiungere A e B:
se A e B sono abbastanza vicini
allora
tracciare il segmento AB
altrimenti
individuare i vertici V1=A,V2,....,Vn=B diuna spezzata simile ad una assegnata
congiungere V1 e V2
...................
congiungere Vn-1 e Vn.
Implementazione del procedimento generale
Realizzare un disegnatore automatico TurboPascal - nel
seguito ci riferiamo alla vs. 3.0 per I.B.M. compatibili con scheda grafica
CGA - di curve ricorsive del tipo generale descritto precedentemente è
un'attività di laboratorio d'informatica e matematica che può
essere affrontata nel corso del triennio in una scuola secondaria superiore.
Tra i prerequisiti sarà richiesta la capacità di usare il costruttore
di tipo 'ARRAY' e di costruire semplici procedure e funzioni. Occorrerà
inoltre aver introdotto la procedura predefinita 'draw' per tracciare un segmento
di estremi assegnati. Le coordinate dei punti sul video dell'elaboratore saranno
riferite al sistema cartesiano discreto che viene reso disponibile con il comando
'graphMode'. Supponendo di rappresentare la spezzata campione con estremi (0,0)
e (1,0), occorrerà utilizzare un metodo per costruire una spezzata simile
a quella ma con estremi A e B qualsiasi. Il modo più semplice è
forse il seguente: detto pq il piano i cui assi coordinati sono descritti dai
versori ![]() e
e ![]() ,
essendo
,
essendo ![]() il vettore perpendicolare
al vettore
il vettore perpendicolare
al vettore ![]() ,
,
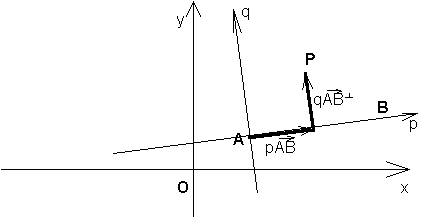
si può riconoscere che, detto P un punto qualsiasi di
coordinate (p,q) nel piano pq, ![]() =
=
![]() +
+ ![]() =
= ![]() + p
+ p![]() + q
+ q![]() o anche,
dette xA e
yA le coordinate di A, xB e yB le coordinate di B, x e y le coordinate di P
nel piano xy,
o anche,
dette xA e
yA le coordinate di A, xB e yB le coordinate di B, x e y le coordinate di P
nel piano xy,
x = xA + p(xB-xA) + q(yA-yB)
y = yA + p(yB-yA) + q(xB-xA).
Un semplice programma in TurboPascal è dunque il seguente:
const nVert=16; type punti=array [1..2] of real; spezzata=array [1..nVert] of punti; var A0,B0:punti; p,q:array[1..nVert] of real; i,n,risoluzione:integer; function dist(P,Q:punti):real; begin dist:=sqrt(sqr(P[1]-Q[1])+sqr(P[2]-Q[2])) end;
procedure determina_vertici(A,B:punti;var V:spezzata); var i:integer; begin for i:=1 to n do begin V[i][1]:=A[1]+p[i]*(B[1]-A[1])+q[i]*(A[2]-B[2]); V[i][2]:=A[2]+p[i]*(B[2]-A[2])+q[i]*(B[1]-A[1]); end end;
procedure congiungi(A,B:punti); var V:spezzata; i:integer; begin if dist(A,B) < risoluzione then draw(round(A[1]),GetMaxY-round(A[2]), round(B[1]),GetMaxY-round(B[2]),1) else begin determina_vertici(A,B,V); for i:=1 to n-1 do congiungi(V[i],V[i+1]); end end;
begin
write('Numero di vertici della spezzata = '); readln (n);
writeln('introduci le coordinate (p,q) dei vertici della spezzata');
for i:= 1 to n do
begin
write ('p[',i,'] = '); read(p[i]);
write ('q[',i,'] = '); readln(q[i]);
writeln;
end;
write('risoluzione del disegno = '); read(risoluzione);
A0[1] := 100; A0[2] := 100;
B0[1] := 200; B0[2] := 200;
graphMode;
congiungi(A0,B0);
readln;
textMode
end.
Analisi di alcune curve ricorsive
Naturalmente le curve ricorsive disegnate automaticamente col metodo descritto sopra sono soltanto delle approssimazioni di curve che possono essere solo immaginate, a cui tendono le curve disegnate quando la risoluzione tende a zero. Un esempio famoso di curva ricorsiva è il "fiocco di neve" di Helge von Koch,
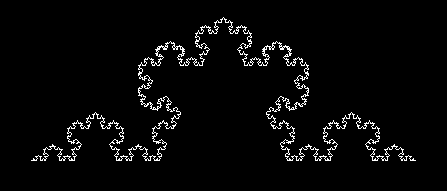
che si ottiene a partire dalla spezzata i cui vertici sono descritti nella tabella seguente
p q V1 0 0 V2 1/3 0 V3 1/2V4 2/3 0 V5 1 0
Un altro esempio di curva ricorsiva nota, con una spezzata di base semplice, è "le chiese" di Dekking

che si ottiene considerando i seguenti vertici di base
p q V1 0 0 V2 1/3 0 V3 1/3 1/3 V4 2/3 1/3 V5 2/3 0 V6 1 0
Naturalmente il programma descritto nel paragrafo precedente offre, data la sua versatilità, la possibilità di studiare altre diverse curve ormai classiche e le loro varianti, ma stimola anche la caccia di altre curve interessanti.

Bibliografia
B.Mandelbrot: Gli oggetti frattali, Einaudi, Torino 1987
S.Carmelo:'Schemi ricorsivi', in: L'insegnamento della matematica e delle scienze integrate', vol.16, n░2, feb.93